弓网系统滑板磨损特性分析与剩余寿命预测

李 斌，隋 意，王智勇，仲丽晓

（1. 辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105； 2. 国网河北省电力有限公司 威县供电分公司，河北 邢台054700）

0 引言

电气化铁路的快速发展对高速列车安全稳定运行提出越来越高的要求.受电弓滑板和接触网导线组成的弓网系统是电力机车的重要组成部分.滑板与接触网导线通过滑动电接触为电力机车提供动力.影响其载流摩擦磨损特性的因素主要有列车时速、波动影响压力载荷、电流、频率、环境等[1].因此，研究滑板的磨损特性、降低滑板的磨耗率、延长其使用寿命，对提高弓网系统运行的经济性具有重要意义.

目前，国内外对受电弓滑板寿命预测的研究还较少，而对于研究受电弓滑板的可靠性、接触表面氧化过程和损害机理等方面的较多.DING T[2]等发现电接触中存在温升和电弧放电，接触面的温升和电弧放电强度随电流增加而增加.碳带磨损量的增加主要是接触面的高温和电弧放电现象引起的.高温引起的热磨损对受电弓接触带的使用寿命有明显影响，电弧腐蚀影响更大.BRAUNOVIC M[3]等基于触点内形成氧化膜的厚度与氧化物的浓度成线性关系，建立了闭合电接触寿命评估模型.BUCCA G[4]等认为弓网需要保持一定的接触压力，如果压力过大，会导致碳滑板的磨损加剧，反之，使受流不稳定，缩短碳滑板的使用寿命.胡文平[5]等建立元件的数学模型，运用累计加权法，将元件的磨损量作为判别寿命的依据.江亲瑜[6]等将离散数学方法与计算机技术相结合，运用数值仿真方法建立磨损的数值仿真模型，提出磨损寿命概率估计的概念.久保田喜雄[7]等研究出的浸金属碳滑板，有效降低了与接触线之间的损耗，从而延长受电弓滑动电接触的使用寿命，替代了金属系烧结滑板，被电气化铁路广泛采用.

本研究利用滑动电接触实验机，在不同条件下进行载流摩擦实验，研究滑板磨损量与剩余寿命的关系，建立基于概率分布的受电弓滑板磨损寿命预测模型，并验证模型的正确性.另外，研究在不同接触压力波动幅度下受电弓滑板的磨损特性.

1 实验设备与材料

为研究载流摩擦磨损对于受电弓滑板寿命的影响，实验所用的实验机加入波动载荷装置，用来模拟波动载荷下弓网系统实际的接触情况，见图1.

图1 滑板磨损实验机 Fig.1 sliders wear testing machine

通过高精度BSM电子天平计量滑板磨损前后的质量变化，确定滑板的磨损量.同时，采用精度为0.01 mm、量程为15 mm的数字电子标尺实时在线测量受电弓滑板厚度的磨损量.通过受电弓滑板的不同磨损量来预测滑板的剩余使用寿命.采用浸金属碳滑板，接触线采用CT110铜接导线，表1、表2分别给出了滑板在实际使用中的磨耗性能和磨耗比性能.实验机的弓网接触压力波动频率为2 Hz，波动载荷分别在（70±10）N和（70±20）N条件下进行磨损特性实验.

表1 滑板使用中的磨耗性能 Tab. 1 wear properties of sliders

表2 滑板磨耗比性能 Tab.2 abrasion ratio properties of sliders

2 实验结果分析

2.1 压力波动幅度下滑板磨损特性分析

在滑动速度为120 km/h，波动载荷幅值分别为（70±10）N和（70±20）N条件下进行磨损实验，通过分析滑板形貌、热成像温度、电弧等实验数据，对受电弓滑板的磨损特性进行分析.

采用XJP-6A型金相显微镜得到在不同实验条件下的受电弓滑板表面形貌，见图2.

图2 波动幅度为10 N 、20 N时滑板表面形貌 Fig.2 surface morphology of slider plate when the fluctuation amplitude is 10 N and 20 N

由图2（a）中看出其接触表面相对平整，但是由于二者发生磨粒磨损的原因，其滑板表面可见明显的机械摩擦划痕.可见在接触压力波动幅度为10 N时，受电弓滑板表面疲劳磨损不明显.由图2（b）可见其表面局部位置发生明显的撕裂裂纹，表面出现深沟和侵蚀坑，主要是由于电弧侵蚀造成的滑板表面磨损增大.

在不同接触压力波动幅度条件下，对受电弓滑板表面温度进行监测，采用非接触式FLIR T420型热像仪测量滑板温度，见图3.图3（a）中滑板表面最高温度为78.8 °C，图3（b）中滑板表面最高达113 °C.由此可见，受电弓滑板表面的最高温度随着接触压力波动幅度的增加而升高，结合滑板所对应的形貌图可知其磨损有所增大.

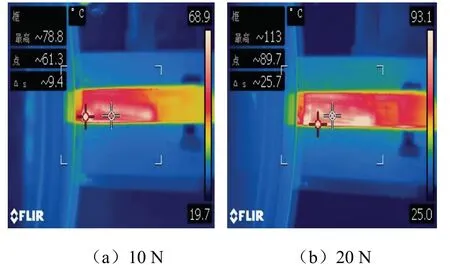
图3 不同压力波动幅度下滑板温度 Fig.3 temperature of pantograph sliders at different pressure fluctuations

在不同接触压力波动幅度条件下，利用AOS S-PRI plus型高速摄像机实时在线拍摄接触导线与受电弓滑板间产生的电弧照片.压力波动幅度分别10 N和20 N时的电弧放电照片，见图4.图4中随着接触压力波动幅度的增大，弓网间电弧放电现象有所增强，由于电弧侵蚀现象造成受电弓滑板表面形貌侵蚀痕迹变多，会出现电弧侵蚀坑等，从而增大滑板的磨损.

图4 不同压力波动幅度下电弧 Fig.4 arc at different pressure fluctuations

通过实验可知，随着弓网系统接触压力波动幅度的增加，受电弓滑板接触表面出现深沟和侵蚀坑等现象，滑板的温度随之增加，其电弧放电现象增强，使滑板的磨损率提高，导致磨损严重，必然减小滑板的磨损寿命，影响机车稳定高效运行.因此，在实际运行中列车应该尽量减小弓网系统接触压力波动幅度，减少滑板磨损.

2.2 不同条件下滑板磨损分析

当实验机运行速度为100 km/h时，在波动载荷幅值为（35±5）N条件下进行磨损实验，图5为实测摩擦力和电流实时变化.

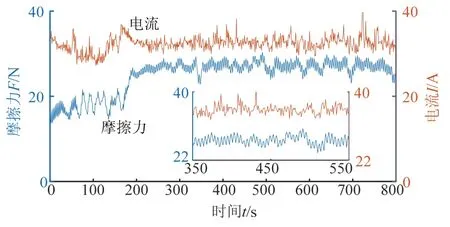
图5 摩擦力和电流随时间的变化 Fig.5 changes of friction and current with time

由图5可见，在相同的实验条件下，摩擦力不恒定，是随时间不断发生变化的.一般将滑板的磨损过程分为磨合期、稳定磨损期、剧烈磨损期，图5中摩擦力从较小的初始值迅速增大，经过一段初始磨合期后进入稳定磨损期.

不考虑磨合阶段，弓网系统工作处于稳定磨损期，采用控制变量法，当接触压力70 N时进行有、无电流介入时滑板磨损率随速度变化实验.图6为滑板磨损率分别在有电流和无电流介入时随速度变化情况.

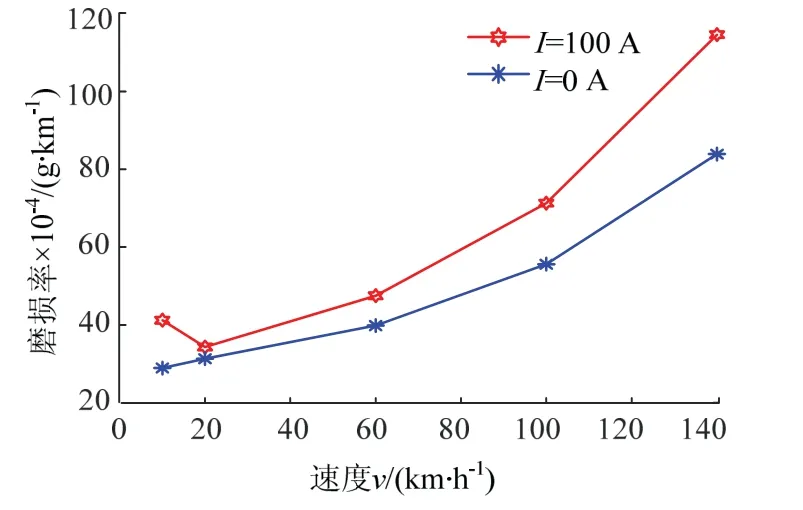
图6 磨损率与速度关系 Fig.6 wear rate change in relation to velocity

由图6可见，磨损率随速度的增大而增大，相同速度条件下电磨损率高于机械磨损率.因为电流产生的焦耳热会使接触区发生微形变，降低材料的机械强度，在接触压力和滑动速度的双重作用下，使磨损率增加；特别是电弧放电的高温作用，会对滑板表面产生严重的电弧侵蚀效应，使磨损率急剧增加.图6中电磨损率在滑动速度为20 km/h时有一个最低值，在速度大于100 km/h时明显上升，滑板在列车高速时磨耗的速度加快.

当考虑磨合期时，分别测得滑板在工作10 min、30 min、60 min、120 min和300 min实验条件下，其磨损量与时间关系曲线，见图7.

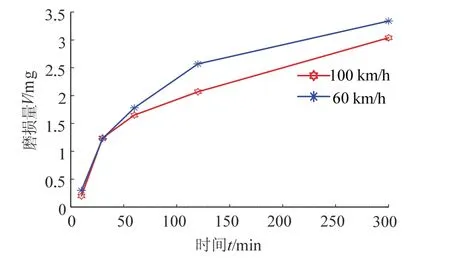
图7 磨损量与时间关系 Fig.7 relationship of wear volume with time

由图7可见，在相同时间内，速度为60 km/h比100 km/h的磨损量大.其主要原因是由于低速度下滑板与接触线之间的磨合期较长，磨损相对严重，导致磨损量较大.

3 滑板的磨损寿命预测模型

3.1 基于可靠性磨损寿命预测模型

决定受电弓滑板剩余使用寿命的主要因素是弓网系统的摩擦磨损，其磨损速率与列车时速、接触电流、波动载荷和材料等相关.因此，对受电弓滑板表面磨损性能和使用寿命的预测，主要考虑系统处于稳定磨损期时的相关参数及其特征值，在该阶段滑板的磨损量与时间成线性关系.当系统在稳定磨损期时，其磨损速率变化不大，其值主要取决于载荷即摩擦表面正压力、运行速度、滑板和接触网导线构成的摩擦副表面材料特性，以及机械加工润滑处理情况等[8]. 在一定可靠度下受电弓滑板的磨损寿命预测模型为

式中，u为磨损速率，10-4g/km；k为摩擦因数；p为摩擦表面正压力，N；v为运行速度，km/h；m值为0.5～3，取1；n为速度因子，受相对运动速度的影响，对于多数摩擦副可取为1[8].

设滑板的总磨损量为WΣ（t），则其可靠度为

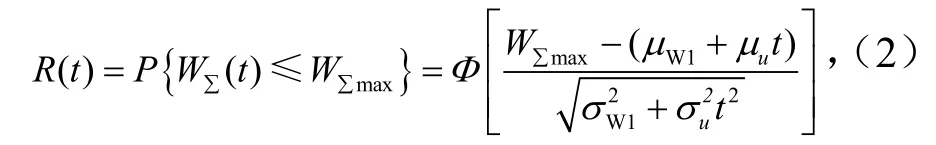
式中，WΣmax为最大允许磨损量，g；t为工作时间，h；σW1、μW1为磨合阶段磨损量标准差与均值，g；σu、μu为稳定磨损阶段磨损量的标准差与均值，10-4g/km；Φ为正态分布密度函数.

当受电弓滑板的磨损可靠度R给定时，由于此时系统处于稳定磨损阶段，磨损速度变化不大，设u为定值，标准差σu趋于零，则滑板的磨损寿命t为

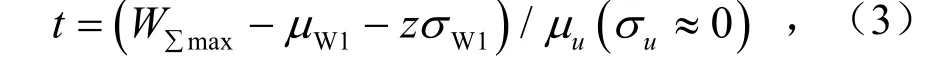
式中，z为安全指数，

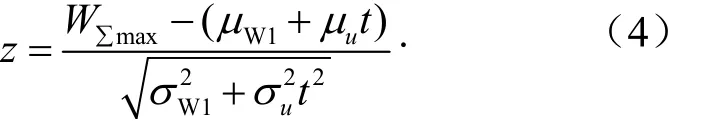
3.2 滑板磨损寿命概率分布模型

文献[9]和文献[10]研究得到，在一定时间内摩擦器件的磨损量寿命分布模型一般近似符合正态分布，当工作于稳定磨损期时，其磨损量和时间基本上成线性关系.这里仅研究弓网系统受电弓滑板工作在稳定磨损期（不考虑磨合期），磨损量随时间的函数变化关系式为

建立滑板磨损量的概率密度分布函数[11]为

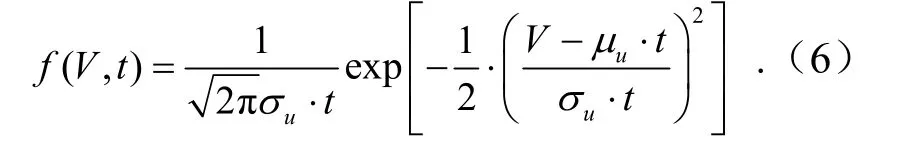
对于式（5），当受电弓滑板磨损量V和时间t在一定范围内时，根据实验获得数据计算受电弓滑板磨损速率u的均值μu和标准差σu，利用Matlab 软件绘制滑板磨损量的概率密度分布函数f（V，t）三维曲线，见图8.由图可见，函数f（V，t）是连续且光滑的，近似符合正态分布.在一般情况下，一定时间t内受电弓滑板的磨损量V不能接近零，更不能为无穷大.

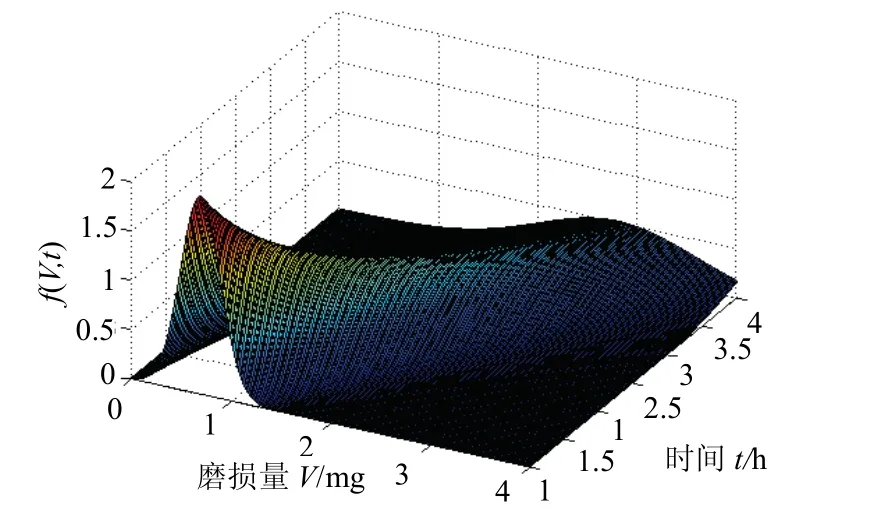
图8 滑板磨损量概率三维分布f（V，t） Fig.8 three-dimensional distribution of the probability f（V，t） of wear volume

将滑板的最大允许磨损量设为Vm，在磨损时间为（tmin，tmax）区间内将其均分为n份（其中n→∞），取在无穷小的时间段值，滑板磨损概率[12-15]为t=ti时连续且光滑的函数值f（Vm，ti），表示为

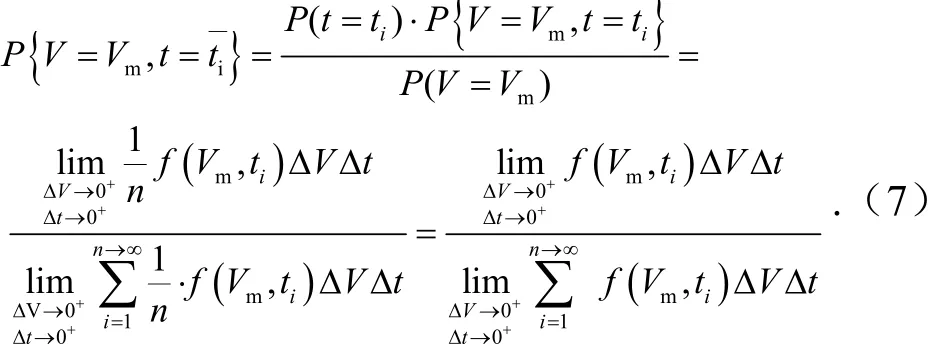
当n→∞时，得到

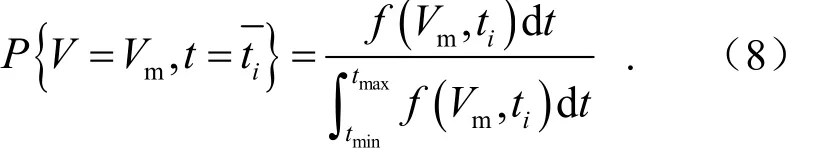
当受电弓滑板的磨损量设定为Vm时，有

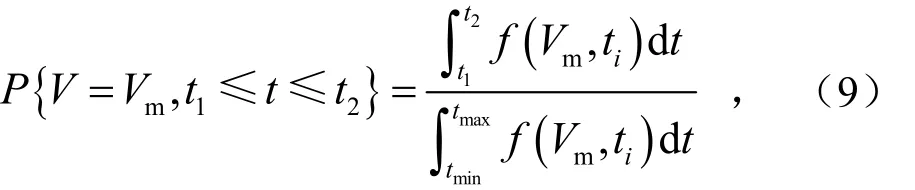
式中，（tmin，tmax）包含（t1，t2）.

将式（9）积分，得到滑板的磨损寿命概率分布函数为

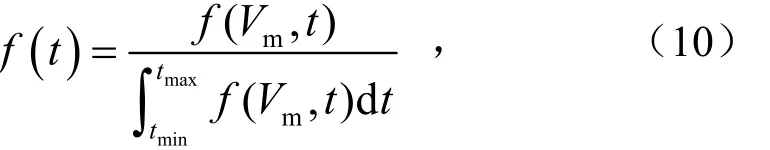
式中，Vm是事先设计滑板时给出的最大允许磨损量，mg；tmin和tmax可通过滑板磨损速率u的均值和标准差求得，对于滑板给定磨损寿命t，其可靠度为

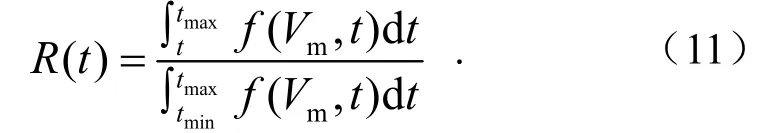
当设定可靠度时，即R（t）=r（0≤r≤1），则滑板的剩余寿命t为

3.3 受电弓滑板磨损寿命预测分析

当受电弓滑板工作于稳定磨损期时，设当可靠度R（t）分别取0.80、0.90、0.95和0.99时，滑板厚度最大允许磨损量Vm=10 mm，根据建立的给定可靠度下滑板磨损剩余寿命预测模型，利用Matlab软件得到滑板寿命预测值与理论计算寿命结果对比分析，见表3.

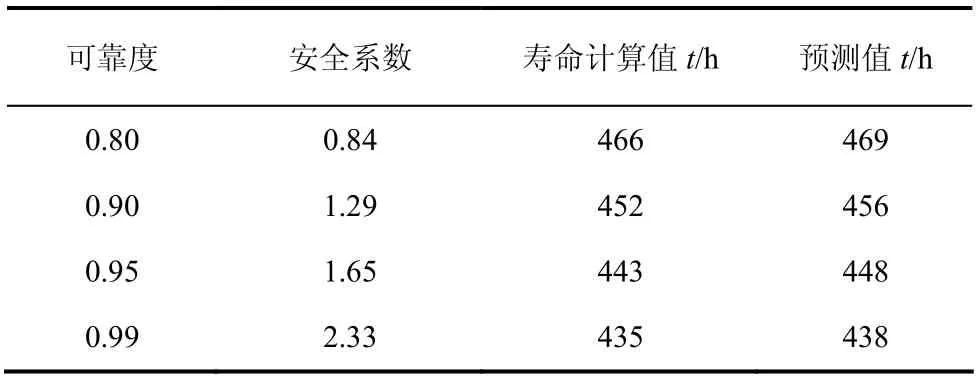
表3 滑板寿命预测值与理论计算值对比 Tab. 3 comparison of life prediction value and theoretical calculation value of pantograph slider

从结果对比来看，本文建立的受电弓滑板磨损寿命预测值与可靠寿命理论计算值较接近，所建预测模型具有一定的准确性.

4 结论

本文利用滑动电接触实验机，以纯铜接触网导线和碳滑板为研究对象，开展了不同条件下载流的摩擦实验，通过实验结果分析和对滑板磨损寿命进行预测研究，得出如下结论：

（1）在不同接触压力波动幅度下，通过滑板形貌、热成像温度、电弧等实验数据，对受电弓滑板的磨损特性进行分析可知，接触压力波动幅度越大，滑板磨损越严重.

（2）通过对受电弓滑板磨损量的研究发现：当给定可靠度时，根据弓网系统电接触剩余寿命与磨损量随时间的变化关系式，能够计算滑板的剩余使用寿命.

（3）考虑到滑板磨损受不同因素的影响，具有不确定性和分散性，建立了滑板在稳定磨损阶段基于可靠度磨损寿命预测模型，通过预测滑板寿命与计算寿命的对比分析，验证了预测模型的正确性.通过预测模型预测滑板剩余使用寿命，减少滑板的更换频率，提高使用寿命，节约运行成本，同时也为列车安全运行提供一定的理论指导.