菱形网格支撑框架结构基于性能的抗震设计方法研究

樊春雷，包献博，郝际平，张海宾，钟炜辉，张凯晨

(1.西安建筑科技大学 土木工程学院，西安 710055；2.西安建筑科技大学 设计研究总院，西安 710055；3.山东高速莱钢绿建发展有限公司，山东 青岛 266000)

随着我国经济的发展和社会的进步，对于住宅建筑的要求越来越高，包括节能环保、建设速度等，而钢结构本身具有得天独厚的优势:工业化程度高、施工现场湿作业少，建筑绿色环保，施工周期短速度快等。因此近年来，国家积极推广钢结构住宅，按照适用、经济、安全、绿色、美观、可循环的要求，推动我国住宅建造方式的创新。钢结构住宅的发展符合我国化解钢铁产能过剩、实现建筑工业化、发展绿色建筑的战略要求[1]。为了适应住宅建筑的建筑美观和使用功能性的要求，目前在结构方面的改进比较多，包括为了不露梁柱而采用的异形柱、壁式柱等，而对于围护体系尤其是抗侧力体系与外围护的有机结合的研究相对较少，导致目前很多钢结构住宅仍然采用砌体的围护方式，不符工业化建筑的理念[2-3]。

对于钢结构而言，抗侧力结构是整个结构最重要的组成部分，其中钢框架-支撑结构是多高层钢结构中常用体系[4]。本文提出一种新型的菱形中心支撑框架(diamond grid braced frames structure，DBF)，通过有限元软件ABAQUS在相同用钢量下对菱形支撑结构与传统的交叉支撑、人字形支撑、单斜杆支撑做了拟静力滞回分析，得到骨架曲线如图1所示，结果证明该DBF通过优化网格形成双重的拉压杆件，提高了结构的冗余度，在保证边柱刚度的情况下与传统的中心支撑相比，不提高支撑用钢量下可以满足结构初始刚度、延性等结构抗震要求，且相比传统支撑减小了支撑面外厚度,方便围护墙体的安装，为支撑围护一体化创造条件。

图1 骨架曲线对比Fig.1 Skeleton curve comparison

在设计中心支撑时，现行抗震设计规范通常基于结构弹性性能，间接考虑结构的非弹性性能。近年来，数次强烈地震给人类造成了巨大的生命财产损失，基于强度的抗震设计方法已经不能满足要求[5]。因此本文根据能量守恒原则，在基于性能的塑性设计(performance-based plastic design，PBPD)的基础上提出了菱形网格支撑的设计方法，可以直接考虑结构的非弹性性能而无需进行评估和迭代，有利于在实际设计过程中推广应用[6]。综合菱形网格的特殊性，考虑支撑对周边框架的影响，提出菱形支撑框架屈服构件和非屈服构件的设计方法，并通过弹塑性非线性动力时程分析进行验证。

1 菱形网格支撑抗侧刚度及承载力

菱形网格支撑在进行内力分析时以单层铰接框架为分析模型，如图2所示。

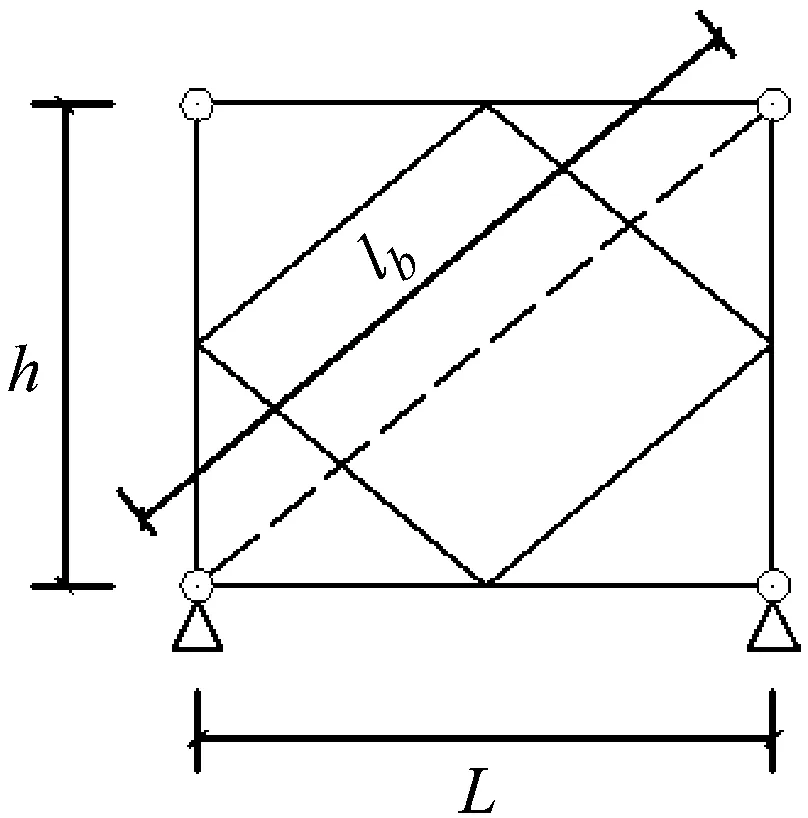
图2 菱形支撑力学模型Fig.2 Mechanical model of diamond support

通过分析，在水平荷载作用下菱形网格支撑发生侧移如图3所示，受力形式可以分为两个阶段：在第一阶段，当支撑处于弹性阶段时，拉压杆件产生相同的应变及应力，支撑对梁和柱产生了附加轴力，如图4(a)所示；在第二阶段，随着水平位移的增加，受压杆件首先达到屈曲承载力而退出工作，此时支撑对框架产生了附加轴力和附加弯矩的影响。下面分别对两阶段分别进行分析。

(a)菱形支撑侧移

1.1 第一阶段

当结构在水平力V的作用下产生了Δ的侧移，此时支撑产生了轴力力F作用于周边框架。由结构力学可知，各杆的应力应变大小均为

(1)

(2)

从而杆件的内力大小为

(3)

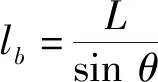
式中：E为弹性模量；Δ为支撑框架顶点产生的侧移；θ为受压支撑与竖直方向的夹角；A为支撑的截面积；lb为框架斜撑的长度。

此时，外力做功为

(4)

内力做功为

(5)

式中,支撑杆件截面相等。结构的抗侧刚度仅由支撑提供，由内外功相等可求得该模型的抗侧刚度

(6)

通过简单的受力分析可知，当支撑全截面屈服时即δ=f，此时支撑框架的承载力为

(7)

1.2 第二阶段

随着侧移角的增大，受压杆件屈曲退出工作，此时支撑框架的受拉形式可以简化为如图4(b)所示的形式。抗侧刚度可以表示为以下。

外力做功为

(8)

内力做功为

(9)

由内外功相等可求得该模型的抗侧刚度

(10)

式(8)～式(10)是相对保守的，根据建筑抗震设计规范，受拉支撑按照屈服承载力设计，受压支撑可以考虑考虑反复变形按屈曲后承载力计算抗压杆件，由于菱形网格支撑的支撑杆件长细比比较小，屈曲承载力和屈服承载力差别不大，因此，为了计算方便公式中屈曲后承载力按屈服承载力的30%计算。此时第二阶段的抗侧刚度为

(11)

第二阶段的最大承载能力为

(12)

(a)第一阶段受力图

2 基于性能的塑性菱形网格支撑设计法

本文将菱形支撑钢框架结构的设计方法推广到基于性能的塑性设计法,该方法采用预选的目标侧移和屈服机制作为性能极限状态，因此设计初需为结构选择一个合理的屈服机构。本为假定菱形支撑框架在罕遇地震作用下支撑构件屈曲或屈服，底层柱底出现塑性铰。根据能量相等原则，采用塑性设计法来设计支撑构件和非屈服构件以便达到预期的屈服机制和性能。

2.1 设计基底剪力

设计基底剪力是PBPD的基础，根据能量守恒原则，结构单调达到目标侧移所需作的功等于等效弹塑性单自由度体系达到相同状态所需要的能量，以此来计算给定的地震水准下的设计基底剪力[7],如图5所示。

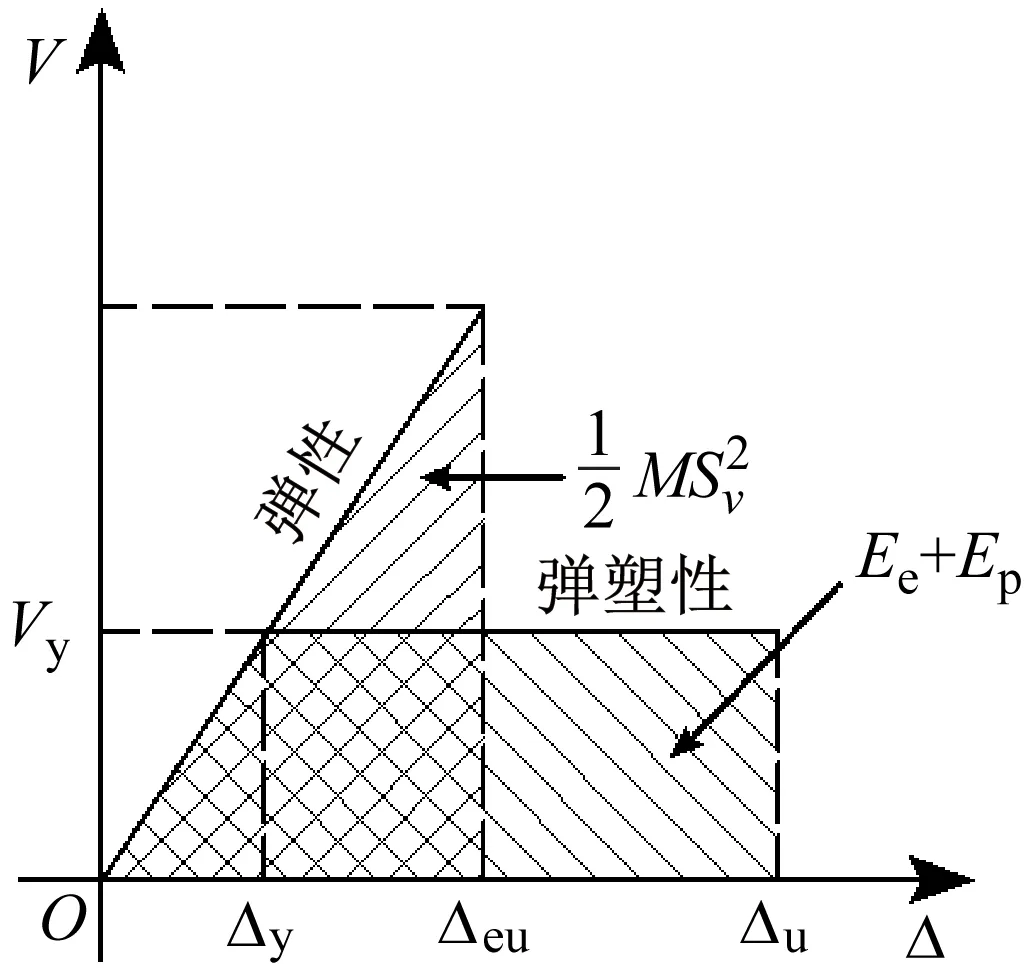
图5 基于性能的塑性设计概念Fig.5 PBPD Concept

(13)

式中：Ee、Ep分别为使结构达到目标侧移所需能量的弹性分量和塑性分量;Sv为设计拟速度谱;Sa为拟加速度谱;T为基本自振周期;M为体系的总质量;γ为能量修正系数。

弹性分析和塑性分量[8]可由式(14)、式(15)给出

(14)

(15)

由式(13)～式(15)得到

(16)

(17)

(18)

式中:γ为能量修正系数，其值取决于结构的延性系数μs和延性折减系数Ru[9]。

2.2 侧向力分布

侧向力分布采用源于结构非线性动力分析、并经验证正确的侧向力分布模式。基于结构非线性分析，Lee等[10]得出了楼层剪力分布系数，将该系数作为菱形支撑钢框架结构在弹塑性状态下侧向力分布模式，该分布模式可以更准确地估计柱端最大需求弯矩，对于高层钢结构还可以考虑高阶振型的影响。

(19)

(20)

式中:Gj和Gn分别为第j层、顶层的质量；hj为第j层的计算高度;Fi为第i层的侧向力;βi+1为第i层的剪力分布系数。

2.3 屈服侧移角

屈服侧移角是用于计算设计基底剪力的PBPD方法的主要参数之一。结构可以看作是一个具有剪切变形和弯曲变形的垂直悬臂梁，因此菱形网格支撑的屈服位移角可以通过叠加剪切变形和弯曲变形得到[11]。

Δ=Δy,f+Δy,s

(18)

式中：Δ为支撑框架顶点产生的侧移;Δy,f为侧移的弯曲分量；Δy,s为侧移的剪切分量。

对于DBF，剪切分量假定柱不存在轴向变形，侧移来自支撑的轴向变形且不同层数的侧移基本相等，而受弯分量则来自柱的轴向变形如图6所示。

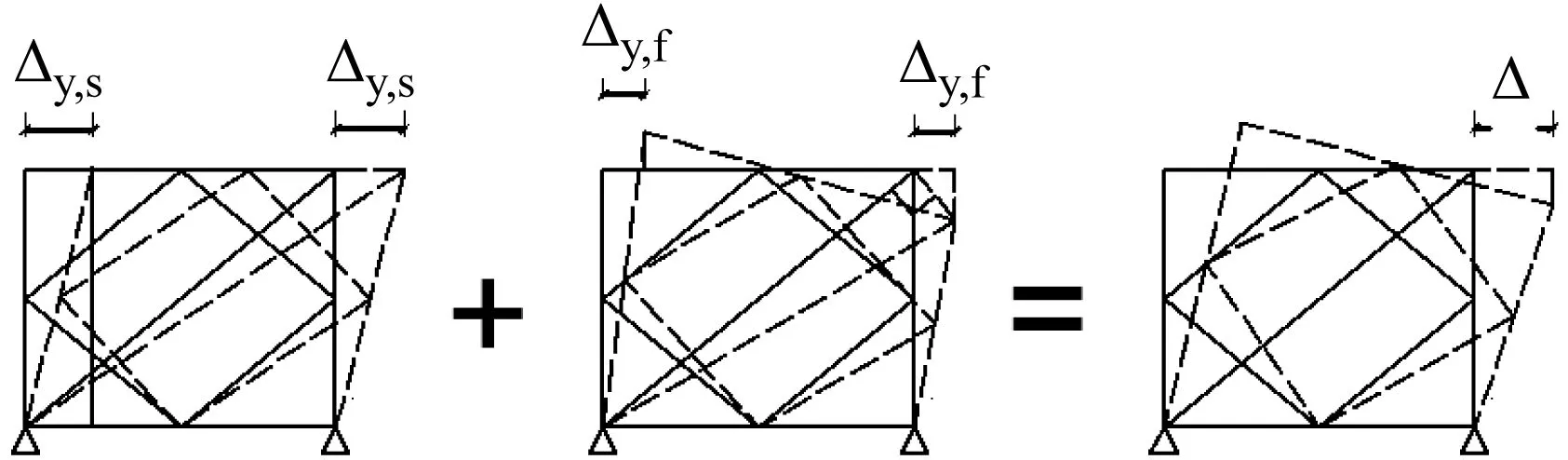
图6 菱形框架支撑的屈服侧移角Fig.6 Yield deflection angle of DBF

对于一层DBF，可得剪切分量为

(22)

其中,L×tanα=h。

Δy,s=εyL2(1+tan2α)=εyh(1+tan2α)/tanα

(23)

因此，屈服位移角的剪切分量可以得到

(24)

式中：θs为屈服位移角的剪切分量；δy为框架斜撑产生的变形；εy为支撑的应变；α为支撑与水平方向的夹角。

由式(24)可知，剪切变形引起的屈服位移角仅取决于支撑的屈服强度和几何参数。因此，在多层DBF的不同层中，屈服状态下的剪切而产生的侧移是可以预期的。

DBF在屈服状态下的受弯位移分量如图6所示，可以将框架视为一个悬臂梁，其中两根柱充当受拉受压的翼缘。受弯变形引起的屈服侧移与框架高度和跨度有关，根据王琼等的研究假设柱中平均轴向应变近似为常数，通过位移协调条件得到由弯曲变形引起的屈服侧移的表达式为

(25)

式中,θf为屈服位移角的弯曲分量。

综上所述可以得到菱形网格支撑屈服侧移角的计算公式

θy=θs+θf，

(26)

2.4 支撑构件设计(屈服构件)

对于支撑构件设计首先要防止钢支撑因局部屈曲位置的低周疲劳开裂而过早退出工作，需要对钢支撑的断裂寿命进行校核，可以通过我国建筑抗震设计规范来校核板件的宽厚比以及长细比。对于强度设计时，假定支撑承担全部设计层剪力，而忽略柱的贡献[12-13]。在地震作用下，通过菱形支撑在第二阶段受力作为支撑设计的基础，根据上面的分析第二阶段抗侧承载力为

V=2.6Aδsinθ

由支撑提供的抗侧承载力大于楼层的层间剪力即得到支撑设计的表达式为

Vyi≤2.6Afsinθ

(27)

式中,f为抗拉强度设计值。

2.5 非屈服构件的设计方法

2.5.1 柱的设计方法

由于菱形支撑几何构形的特殊性，支撑拉杆与压杆之间在柱子上所产生的水平不平衡力对边柱有不利影响。因此保证边柱的安全是设计菱形支撑的重点之一。假设柱初步设计时仅需考虑轴向荷载，后续通过软件对柱的截面尺寸进行微调。柱轴力主要来源于重力荷载和支撑力的竖向分量。以单层菱形网格支撑框架为例，在受力形式上主要分为两个阶段。

(1)第一阶段

由图4(a)可知，单层边柱的最大附加轴力为

Fi=2Aifycosθ

(28)

需要说明的是作用于梁段的竖向分力互相抵消，对边柱无轴力贡献。附加竖向力层层叠加，到底层时边柱的轴力会很大。支撑对一侧边柱的附加轴力是有利的，但是水平荷载有两个方向，因此每个边柱均需要考虑边柱附加轴力的不利影响。通过上面的方法求得附加轴力再叠加上结构其余的竖向荷载，便可得到实际轴力的准确值[14]。

在第一阶段支撑没有全截面屈服，对柱的水平力互相抵消不产生附加弯矩。

(2)第二阶段

由图4(b)可知，受压杆件退出工作后，受压杆件对边柱的最大附加轴力为

Pi=F2cosθ=Aifycosθ

(29)

第二阶段网格支撑受压支撑屈曲后，此时拉杆和压杆对边柱的附加水平力不再保持平衡，拉杆对边柱的水平分力产生了附加弯矩。此时菱形网格支撑的附加水平不平衡力为

Fx=F1sinθ=Aifysinθ

(30)

如图7所示，由附加水平力产生的附加弯矩为

图7 柱的附加弯矩Fig.7 Additional bending moment of the column

(31)

综上所述，支撑框架边柱属于压弯构件，要确定边柱截面，首先需要明确极限状态下边柱所受的轴力与弯矩。边柱所受的轴力由两部分组成，支撑传来的附加竖向力及框架本身承受的竖向荷载[15-16],PG可根据楼层的荷载估算确定。则边柱的轴力为

(32)

初设时，假设梁柱铰接，故梁端几乎没有弯矩传递给柱，框架边柱的弯矩由支撑传来的附加弯矩形成

M=Mmax

(33)

边柱的极限弯矩及轴力确定后即可根据压弯构件的验算公式根据两阶段初步确定边柱的截面以及惯性矩。设计轴力需求可由控制两阶段的极限状态来确定。值得注意的是，上述方法假定所有的支撑同时达到极限状态。这一假定可能偏保守，特别是对于高层建筑的低层柱设计。

2.5.2 梁的设计方法

在支撑框架结构中，为了保证结构受力连续，支撑一般都是沿层布置，当相邻两层的支撑截面尺寸一样时，菱形网格支撑对梁受力互相抵消，对梁无特殊要求，只需保证在支撑与梁的节点位置应力集中不产生破坏即可。而当相邻楼层设计的支撑截面不一样时，在第二阶段由于支撑在梁上的节点产生不均匀受力产生对梁的附加轴力和附加竖向力，如图8(a)所示。同时第二阶段在框架的顶层，支撑会对梁产生附加轴力和附加竖向力,如图8(b)所示。在初步设计与支撑相交的横梁时，假定支撑不承担任何重力荷载，同时将梁可看作简支梁。接下来对跨层梁和顶层两种情况分别分析。

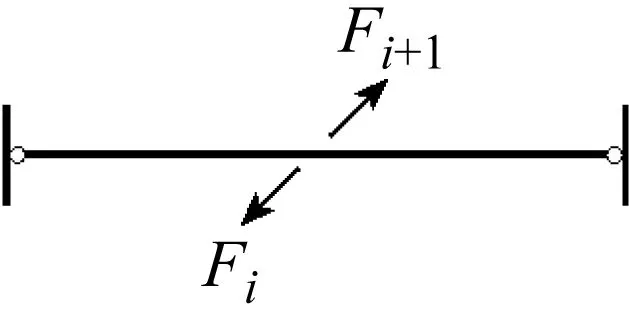
(a)跨层梁受力示意图

当梁为跨层梁时附加弯矩为

(34)

当梁为顶层梁时附加弯矩为

(35)

菱形网格支撑对梁的不利影响并不大，因为一般相邻层数的支撑截面不会差距太大，在顶层是承担的层间剪力不大所以支撑截面也不会太大，同时由于次梁和楼板可以在平面外给主梁提供侧向支撑作用和附加刚度，因此在对梁设计时，可以根据现行规范[17]只进行强度校核，而不进行稳定验算。

综上所述，采用 PBPD 设计菱形中心支撑钢框架的步骤如图9所示的流程图。

图9 菱形支撑框架设计流程图Fig.9 Flow chart of DBF design

3 算例及其分析

3.1 工程概况

该设计工程为12层3跨菱形网格支撑钢框架结构，层高3.6 m。建筑物位于8度抗震设防区，设计地震基本加速度为0.30g；建筑场地为Ⅱ类场地土，设计地震分组为第二组；GB 50009—2012《建筑结构荷载规范》[18]按做法统计，其中楼面恒(活)荷载为4.15(2)kN/m2，屋面恒(活)荷载为5.1(2)kN/m2；支撑、梁、柱以及其他构件均采用Q235钢材，框架由于次梁的存在，楼板的长宽比大于2，可以按照单向板进行传力并计算。通过PBPD设计两种结构包括菱形支撑框架、和交叉支撑框架，为了将菱形网格支撑与传统的交叉支撑框架的性能进行对比，两种结构采用相同的框架尺寸，如图10、图11所示。

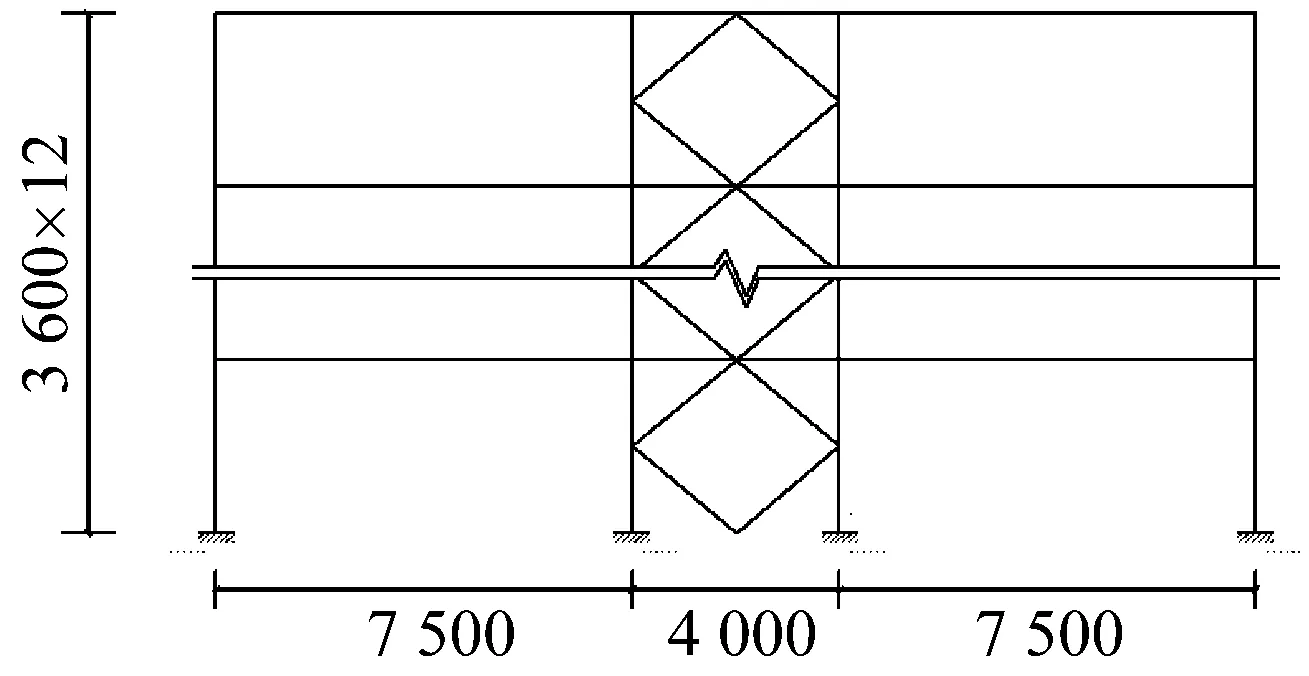
图10 菱形支撑框架立面图(mm)Fig.10 Elevation drawing of diamond braced frame(mm)

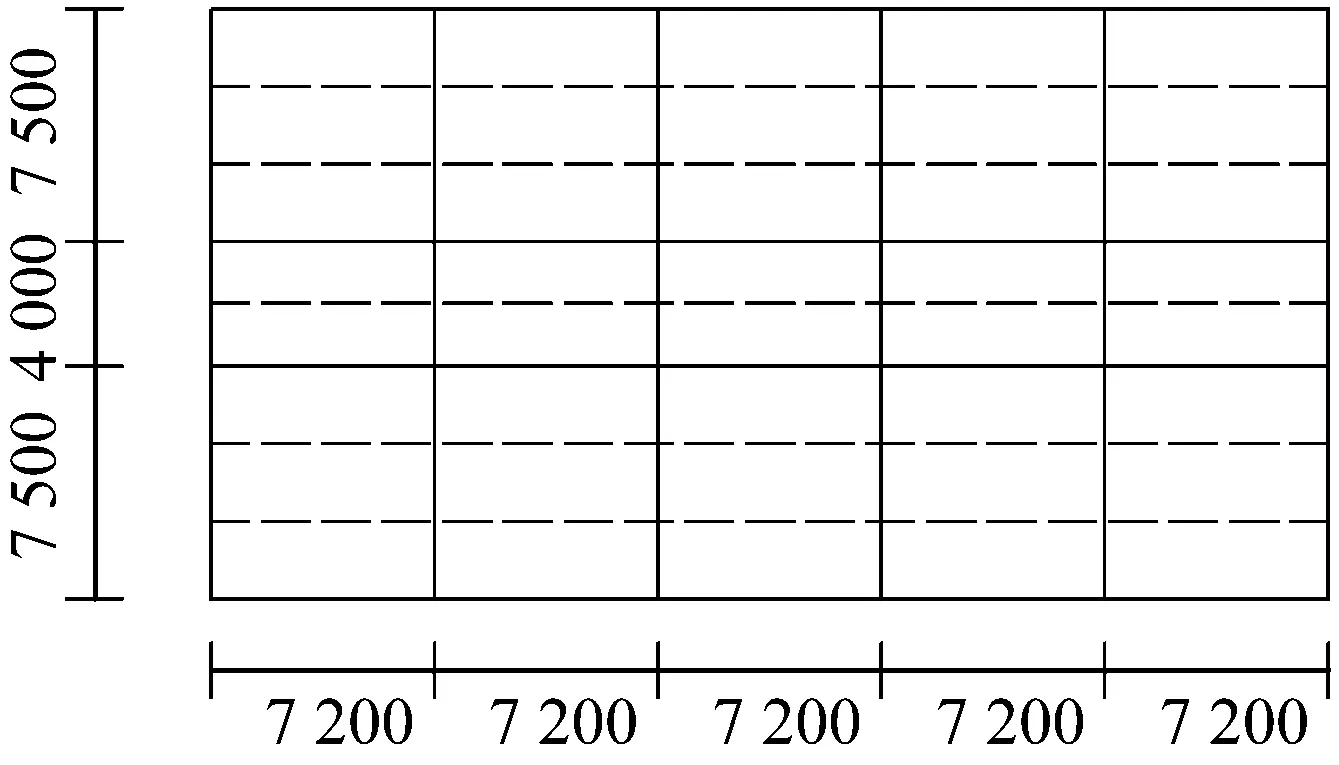
图11 菱形支撑框架平面图Fig.11 Plan of diamond braced frame

3.2 设计基底剪力和侧向力分布

3.2.1 估算周期

根据GB 50009—2012《建筑结构荷载规范》可知:

T=0.10n=1.2 s

(36)

3.2.2 确定屈服侧移角和目标侧移角

根据2.3节的分析，菱形网格支撑的屈服层间侧移角可由层间侧移角的剪切分量和弯曲分量来给出，对于支撑钢框架结构，设计基底剪力按照性能指标来确定，8度罕遇地震作用，最大层间侧移角为1.5%。

3.2.3 加速度反应谱确定

根据GB 5011—2010《建筑抗震设计规范》加速度反应谱Sa可按设防烈度、场地类别、设计地震分组和结构结构自振周期以及阻尼比确定。

3.2.4 设计基底剪力计算

根据上述确定的参数，由式(8)即可计算设计基底剪力。所有重要设计参数的计算值如表1所示。

表1 计算参数Tab.1 Design parameters

3.2.5 侧向力分布计算

由式(16)～式(17)得到设计层间剪力后，根据式(19)将层间剪力进行分配，分配结果如表2所示。

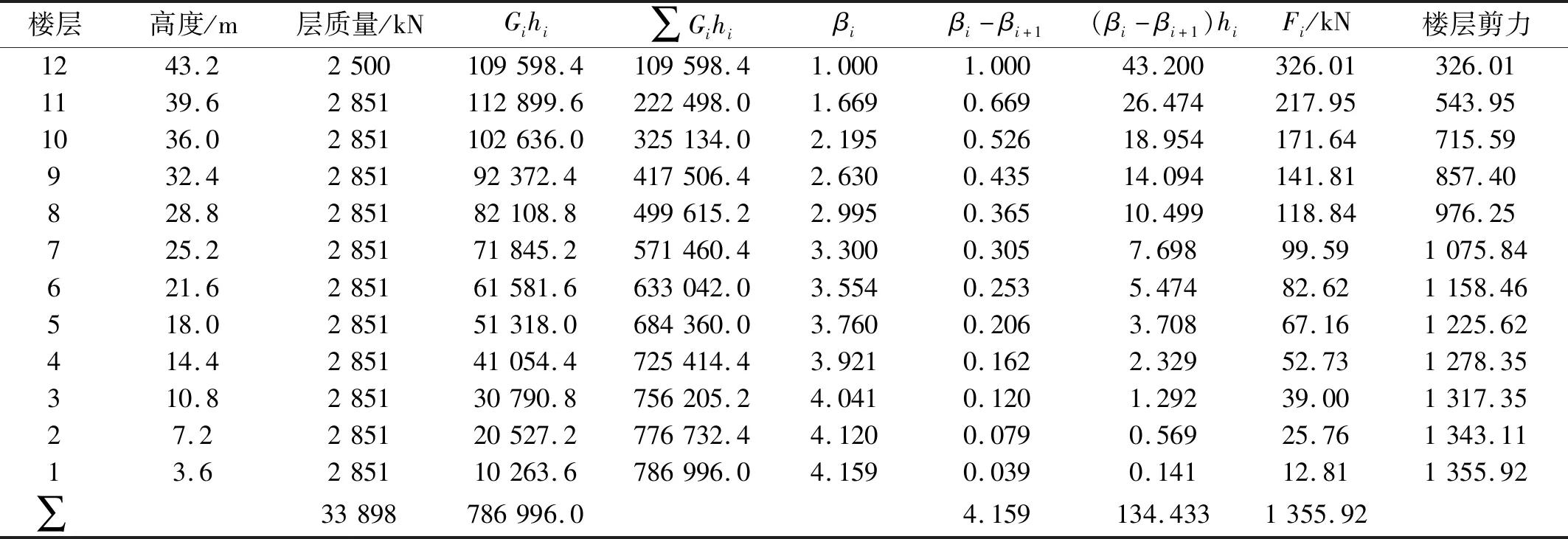
表2 PBPD侧向力分布计算Tab.2 Lateral force distribution calculation for PBPD frame

3.3 构件设计

通过3.2节的计算结果进行构件设计。设计内容分为两部分:一部分为屈曲构件设计，根据各个楼层分配的剪力进行支撑设计，作为指定屈服构件，支撑根据强度、断裂寿命和紧凑性准则来设计;另一部分为屈曲构件设计，作为指定非屈服构件，梁柱采用能力设计法设计。设计参数和最终的设计结果如表3、表4所示。交叉支撑参考文献通过式(37)计算。

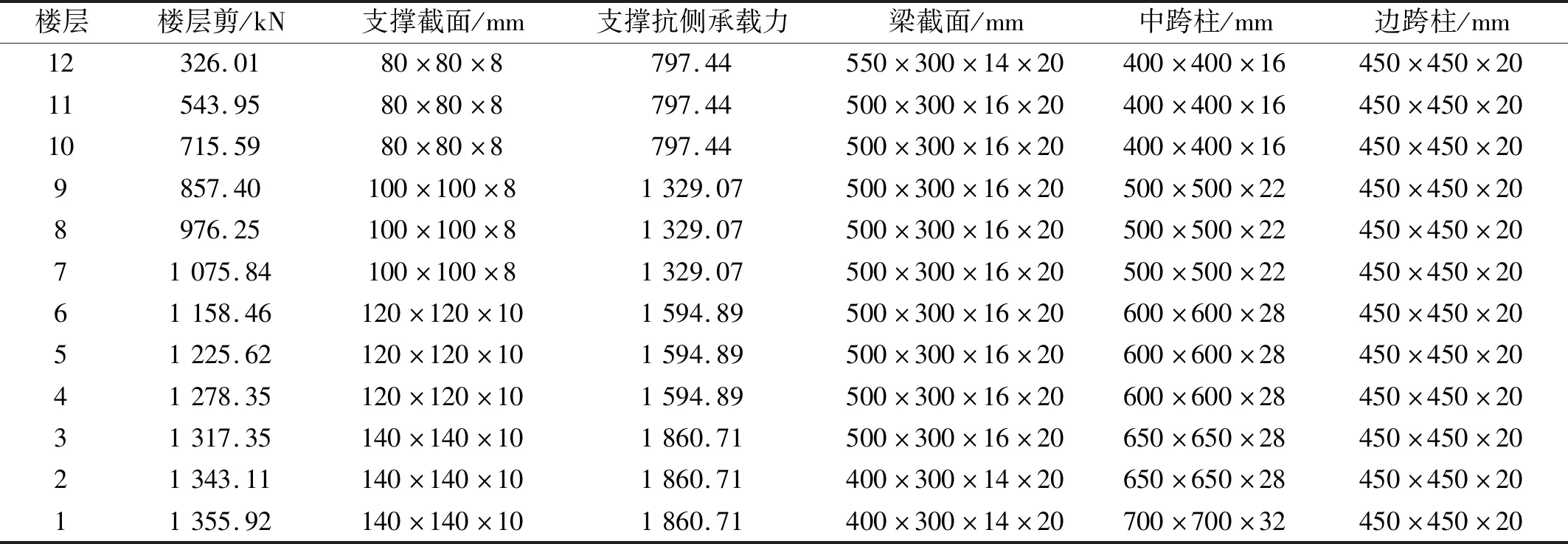
表3 菱形支撑框架设计参数Tab.3 Design parameters for DBF

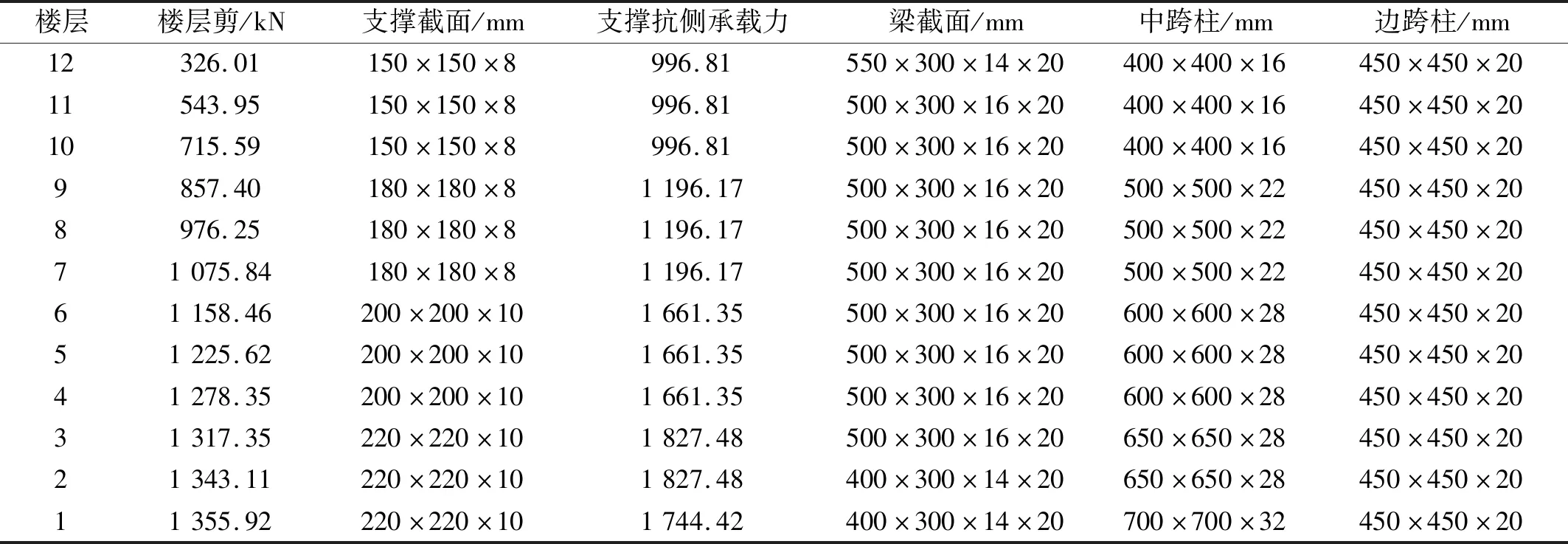
表4 交叉支撑框架设计参数Tab.4 Design parameters for X-braced frame

Vi≤(Py+0.3Pcr)icosαi

(37)

式中：Vi为等效单跨框架的第i层剪力；Py为支撑构件屈服承载力；Pcr为屈曲承载力；α为支撑与水平面的夹角。

4 动力时程分析结果

4.1 模型参数

选取7条地震波通过弹塑性动力时程分析对3.4节结果进行验证，地震波的反应谱、平均反应谱与规范谱的对比，如图12所示，各主要周期上平均反应谱与规范谱相差最大值满足小于20%的“统计意义相符”规定。同时所选地震波在弹性分析时，计算所得到的结构底部剪力的平均值不应小于振型分解反应谱法计算结果的65%，多条时程曲线计算所得的结构底部剪力平均值不应小于振型分解反应谱法的80%，通过对地震波进行验算，各条地震波满足规范规定，如表5所示。

表5 地震波验算Tab.5 Checking calculation of seismic wave

图12 地震波反应谱和规范谱对比Fig.12 Comparison of seismic response spectrum and gauge spectrum

计算模型的钢材选用双折线随动强化模型，如图13所示，该模型的骨架曲线，如图14所示。钢材弹性模量E为206 000 MPa，二次刚度E0为1%E，泊松比μ=0.3，模型考虑了Bauschinger效应，滞回时可考虑反向加载屈服强度下降的现象，卸载刚度与再加载刚度相等,如图14所示。

图13 钢材本构Fig.13 Constitutive relation of steel

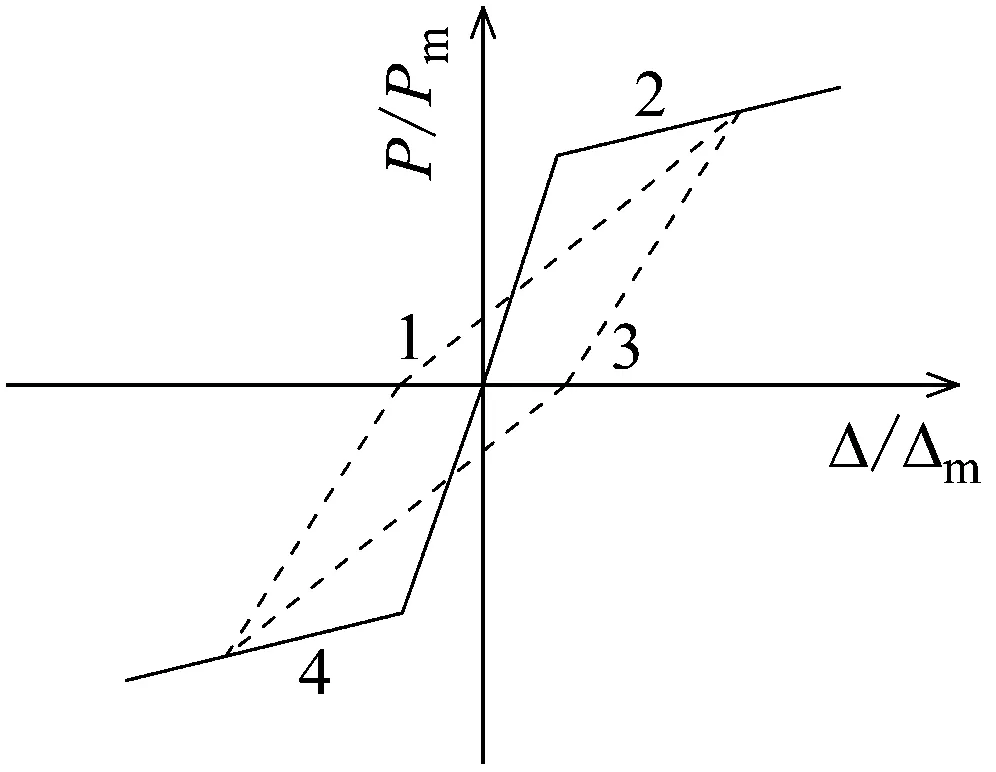
图14 骨架曲线恢复力模型Fig.14 Restoring force model of skeleton curve

4.2 关键构件的滞回性能

菱形支撑的滞回曲线，如图15所示。骨架曲线形状饱满，证明菱形网格支撑结构的抗震效果和耗能能力比较好，且在罕遇地震下支撑会首先发生塑性变形，能够承担第一道抗震防线的作用。菱形支撑框架结构在水平荷载作用下会对框架边柱和梁产生不利影响，因此在使用菱形支撑框架结构时，保证框架的安全尤其是边柱不被破坏尤为重要。边柱的滞回曲线，如图16、图17所示、梁的弯矩滞回曲线，如图18所示。由边柱和梁滞回曲线可知，通过本文介绍的菱形网格支撑框架结构设计方法梁柱基本处于弹性阶段，能够保证周边框架的安全。

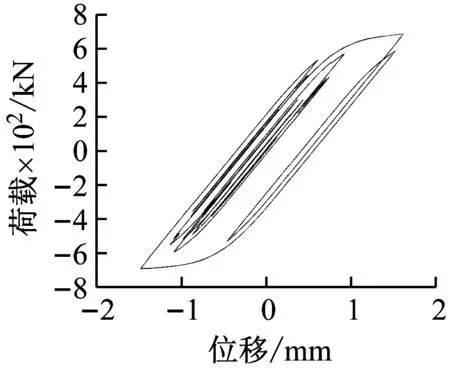
图15 支撑轴力滞回曲线Fig.15 Hysteretic curve of support

图16 柱弯矩滞回曲线Fig.16 Hysteretic curve of column moment

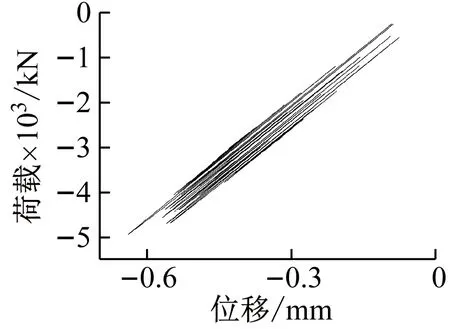
图17 柱轴力滞回曲线Fig.17 Hysteretic curve of column axial force

图18 梁弯矩滞回曲线Fig.18 Hysteretic curve of beam bending moment

4.3 层间位移角分析

两种结构在罕遇地震作用下的层间位移角及层间剪力，如图19所示。通过对比，同一种结构在不同的地震波下层间位移角的最大值并不一定出现在结构同一层，层间位移角的最大值沿结构层数的变化规律也并不完全相同，这说明了地震波时程分析具有离散性。由多条地震波分析结果可知，层间位移角的平均值和包络图更能体现不同地震波分析结果的共性，由图19(c)～19(d)可知菱形支撑框架和交叉支撑框架的最大层间位移角出现在第10层。由PBPD法设计的支撑框架结构在地震波作用下结构最大层间位移角和层间剪力沿楼层均匀分布，这表明结构的非弹性性能沿楼层分布较均匀，各楼层可以同时散相当的地震能量。同时按基于性能的塑性设计法设计的框架支撑结构各层最大层间位移角均小于目标位移角限值1.5%，表明结构满足目标性能要求。

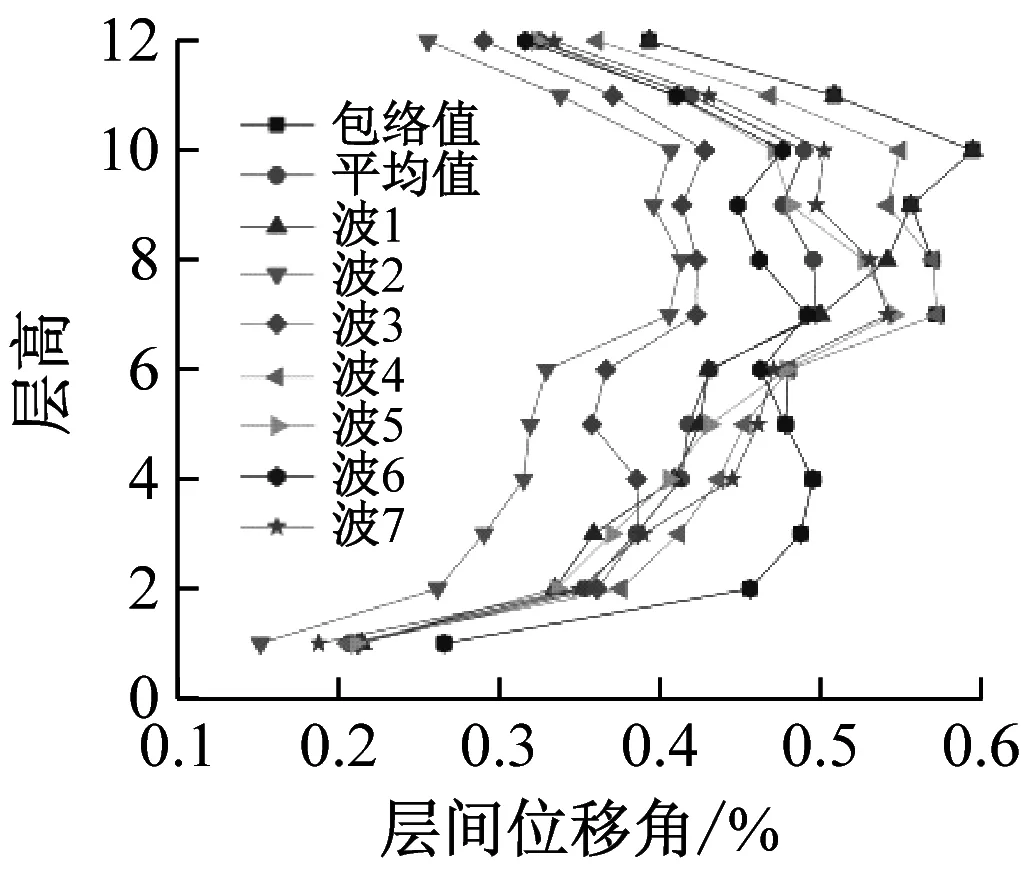
(a)菱形支撑层间位移角

菱形支撑与传统交叉支撑在地震作用下的产生了基本相同的层间位移角，但是菱形支撑大大减小了支撑的截面，相比于交叉支撑截面外面厚度最大减小了100%，最小也减小了57%。由此可知，菱形网格支撑保证结构抗震要求下能够减小支撑截面。

5 结 论

(1)本文提出了一种菱形网格支撑，通过减小支撑面外厚度给结构外围护墙体的安装留出足够的富余度，有利于发展钢结构住宅产业化、支撑维护一体化。

(2)通过分析菱形网格支撑的力学性能以及PBPD设计方法，提出了菱形网格支撑基于性能的塑性设计方法，该方法考虑了支撑对非屈服的不利影响，并推导了菱形支撑的屈服位移角，不需要进行评估和迭代，概念清晰，过程简单，便于推广。

(3)通过动力时程法评估了通过PBPD法设计的菱形支撑框架结构的抗震性能，并结果表明通过PBPD法设计的支撑结构的非弹性性能沿楼层分布较均匀，各楼层可以同时散相当的地震能量，结构满足目标性能要求。

(4)通过动力时程分析对比，在保证边柱安全的情况下，菱形支撑能够提供足够的抗侧刚度保证结构的抗震性能，同时大大减小了支撑截面尺寸。