基于流固耦合的降载空化器高速入水数值研究
李 鸿,李光磊,刘志远,郑可心,高晓初,李 涛
(1.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.哈尔滨汽轮机厂有限责任公司,哈尔滨 150046)
结构入水是典型的高度非线性瞬态流固耦合过程。由于理论研究对弹性体入水过程求解具有一定局限性,实施等比试验具有一定的困难,目前国内外学者大多采用数值模拟方法对入水问题进行研究。
Karman[1]基于动量守恒定律,将飞机模型简化为二维楔形体,建立边界元模型进行计算,并引入附加质量的概念,得到了入水冲击载荷的计算方法,为今后的研究奠定了基础。潘光等[2]使用Msc.Dytran软件对鱼雷入水过程进行了数值仿真,得到了不同工况下的冲击压力峰值和压力分布,对比分析了不同入水速度和不同入水角度对鱼雷壳体所受冲击载荷的影响。Shi等[3]基于任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)算法对水下航行器高速入水过程进行了数值模拟,基于罚函数法计算了耦合面的冲击载荷,结果表明入水冲击载荷随入水速度的增加而增加,且其峰值与速度的平方成正比。Derakhshanian等[4]分别采用有限体积欧拉法、有限差分欧拉法及ALE法对弹体模型斜入水冲击问题进行了对比研究,同时结合试验分析了不同惯性矩及中心对动力学特性的影响。孙玉松等[5]基于多介质ALE方法对弹体高速入水冲击载荷进行了分析,得到了头型对入水载荷峰值及其持续时间的影响规律,分析了入水角度对入水冲击载荷的影响。Gao等[6]基于雷诺平均数方程(Reynolds-averaged Navier-Stokes,RANS)和六自由度刚体运动方程对弹体高速斜入水问题进行了研究,结果表明:速度衰减规律主要受弹体长度及头部形状的影响,入水速度及角度对其影响不大。Chen等[7]开展了不同头型的空化器20°斜入水试验研究,同时结合ANSYS Fluent仿真分析了入水速度与质心的加速度响应及轴向抨击载荷的耦合规律、阻力系数与入水位移的关系等。卢丙举等[8]采用混合模型并结合动网格技术对超空泡航行器高速入水过程进行研究,分析了不同入水速度及航行器头部是否含有通气口对入水冲击载荷的影响规律,发现头部通气可以有效降低入水瞬间的轴向过载。Panciroli等[9]基于光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法并结合试验研究了楔形体以自由落体方式入水的冲击载荷,对比分析了刚体模型和弹性体模型对楔形体入水冲击力的影响。Yan等[10]基于SPH方法对水下航行器高速入水瞬间的冲击载荷进行研究,结合试验分析了入水速度、入水角度及攻角等对入水轴向和径向冲击加速度的影响。Ahmadzadeh等[11]基于耦合的欧拉-拉格朗日(coupled Eulerian-Lagrangian,CEL)方法对小球自由落体冲击入水过程进行研究,考虑了层流延伸的黏性效应,忽略湍流效应对结构冲击载荷的影响,分析了不同密度球体入水的位移及空泡形状的变化规律。
结构入水瞬间遭遇较高的抨击载荷会造成结构破坏,过载过高会引起内部零器件的失灵。为实现结构入水缓冲降载,本文采用泡沫铝材料对空化器进行了入水降载设计;基于MSC.Dytran的一般耦合方法,对比研究了铝合金空化器与降载空化器的入水响应特性,探讨了泡沫铝的降载效能。
1 理论基础
1.1 耦合机理
基于一般耦合方法的流固耦合计算通过一层固定在结构上的封闭耦合面传递流场压力及固场位移,不断交替求解;其中,固场采用基于拉格朗日体系的有限元法,流场采用基于欧拉体系的有限体积法,耦合面两侧的质量及动量输运满足守恒关系。
1.2 关键技术
对于结构入水这类瞬态动力响应、高度非线性问题的研究,时间域的离散采用显示时间积分法。计算时间步为n内显示求解方法的运动微分方程有如下形式
Man=Fe,n-Cvn-Kdn=Fr
(1)
式中:Fe,n为外载荷矢量;Fr为惯性力矢量;M、C与K分别为结构质量阵、阻尼阵与刚度阵;an、vn与dn分别为节点的加速度、速度与位移;加速度可以通过质量阵求逆再与惯性力矢量求积得出,单元质量分布在节点上,各自由度下节点的加速度求解归结为式(2)的一元一次方程
ani=Fr,ni/Mi
(2)
加速度在各时间步内为常数,采用中心差分法进行时间推进,进一步得到节点的速度及位移响应的表达式为
v(n+1)/2=v(n-1)/2+an(Δt(n+1)/2+Δt(n-1)/2)/2
(3)
dn+1=dn+v(n+1)/2Δt(n+1)/2
(4)
结构高速入水问题中,流体内部会产生十分复杂的冲击波。在数值求解中,网格的离散造成冲击波速的不连续,会造成压力、密度及节点加速度和能量的跳跃。基于显式中心差分方法对动力学方程进行时间积分,由于没有算法阻尼的概念会引起高频的数值噪声。因此,压力项中人工体积黏性Q的引入使得强间断的冲击波连续化,对抑制数值噪声至关重要,如

(5)
式中:d为单元特征尺寸;c为材料声速。本文取CQ=0,CL=0.06。
2 仿真与验证
2.1 数值模型简介
降载空化器包括空化盘、泡沫铝及气缸3个部件,其初始位置距水面20 mm;具体地,空化盘头部厚度6 mm,直径26.6 mm,空化盘长度90 mm,泡沫铝内外径分别为3 mm与13.3 mm,气缸壁厚11.25 mm,其余详细尺寸见图1;空化盘与气缸采用铝合金材料,空化盘采用DMAT24模型描述其应力应变关系,并通过Cowper-Symonds模型考虑其高速入水抨击下的应变率响应式(6),不考虑材料的失效;气缸采用刚体模型MATRIG,具体参数见表1。
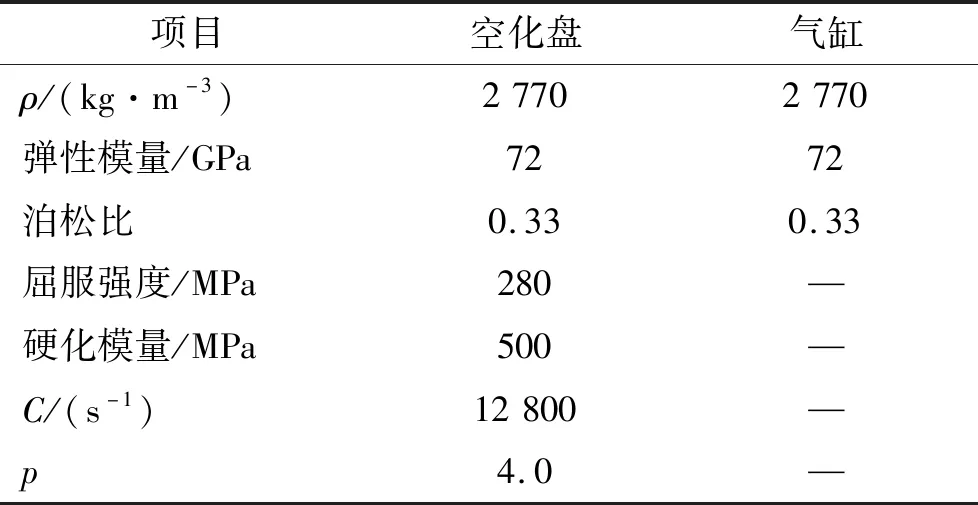
表1 铝合金材料属性Tab.1 Material properties of Aluminum Alloy
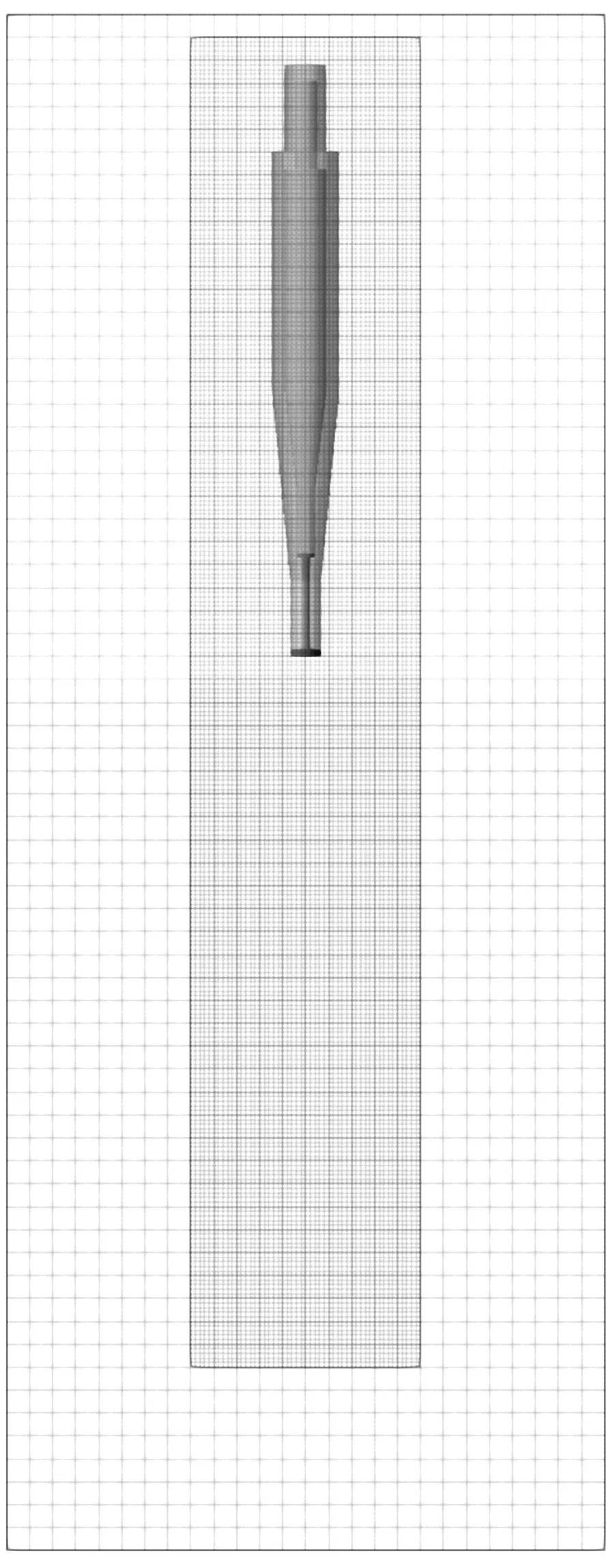
图1 数值模型(mm)Fig.1 Numerical Model(mm)
(6)

研究表明,当泡沫铝应变率低于10 s-1时对其动态应力影响不大,本文采用FOAM1材料模型描述其准静态压缩时的应力-应变行为[12],如图2所示。该模型的三维空间屈服面为球面,用主应力表示为式(7),其中半径Rs=f(Re),Re满足式(8),函数f即泡沫铝的本构方程。

图2 泡沫铝本构模型Fig.2 Constitutive model of foam Aluminum
(7)
(8)
流场模型的描述利用了Graded-Meshes技术(如图1),空化器附近及其运动轨迹上的网格进行了加密;全局欧拉域尺寸为0.52 m×0.52 m×1.34 m,水深0.76 m;盒型加密区尺寸为0.20 m×0.20 m×1.16 m,水深0.60 m。结构入水问题涉及跨介质航行,为考虑初始大气压强的影响,本文考虑了空气的作用。空气压力与密度及比内能关系采用γ率状态方程描述(式(9)),γ=1.4,通过给定比内能e=2.068×105J/kg以及密度ρ=1.225 kg/m3进行大气压力的初始化;水的压力p与密度ρ及比内能e的关系采用如下(式(10))多项式状态方程描述
p=(γ-1)ρe
(9)
p=a1μ+a2μ2+a3μ3+(b0+b1μ+b2μ2+b3μ3)ρ0e
(10)
式中:μ=ρ/ρ0-1;ρ0为初始密度,详细参数见表2。

表2 水的材料参数Tab.2 Material properties of water
本文考虑流体材料的黏性,其应力张量tij定义为式(11);sij为应力偏张量(式(12)),ed,ij为应变偏张量,μ为流体黏性系数;p为压力,其与密度关系满足式(13),体积模量K=a1。
tij=-p·δij+sij
(11)
sij=2μ·ded,ij/dt
(12)
dp/dt=K/ρ(dρ/dt)
(13)
2.2 研究内容
相较于斜入水,结构物垂直入水将遭受更高的抨击载荷。本文以空化器垂直入水为研究背景,分别对铝合金空化器与降载空化器以不同初速度的入水过程进行了数值模拟,二者构型一致,差别在于铝合金空化器整体均为铝合金材质,质量为1.77 kg,降载空化器质量为1.70 kg。表3为具体工况描述,字母A与F分别表示铝合金空化器与降载空化器,数字表示入水速度。

表3 计算工况Tab.3 Study Case
2.3 数值方法验证
本文以Chen等的试验研究为基础,对入水速度v=70 m/s及90 m/s的工况进行了数值模拟,验证了一般耦合方法的可靠性,图3为验证模型。阻力系数指标定义如式(14),其中空化器弹头半径R=10.55 mm,表4结果显示误差在1.2%内。另外,70 m/s情况下的轴向力的对比也基本吻合,如图4所示。

图3 验证模型Fig.3 Verification model

图4 轴向力对比验证Fig.4 Comparison and verification of axial force

表4 阻力系数Tab.4 Drag coefficient
CD=F/(0.5ρ0πv2R2)
(14)
3 结果与分析
如下图5展示了降载空化器180 m/s入水时,从初始位置运动不同距离时的空化效果以及泡沫铝的压缩变形。同时给出了泡沫铝构件特征单元随降载空化器整体位移的应力响应,如图6所示,其中单元1靠近空化盘,单元2位于泡沫铝构件轴向的中间段,单元3靠近气缸。

(a)x1=0.038 7 m

图6 泡沫铝应力响应Fig.6 The stress response of foam Aluminum
结果显示,当降载空化器位移达到0.038 7 m时,即入水瞬间,靠近空化盘头部的泡沫铝(单元1)的应力迅速达到屈服平台;而后保持平台应力,当位移达到0.073 9 m时开始发生硬化;随着入水抨击载荷的降低,又发生了一定程度的回弹,应力降并伴随着一定程度的振荡;随着远离空化盘头部,泡沫铝的应力响应存在一定滞后;泡沫铝两端与铝合金材料连接处的应力响应幅值高于中间段泡沫铝。
3.1 加速度响应规律
图7为空化器不同初速度入水情况下的气缸加速度与位移耦合规律曲线。从总体上看具有泡沫铝降载机构的空化器在入水过程中,气缸的加速度响应会出现数次突变的行为,与泡沫铝的应力响应趋势一致。第一次出现在入水瞬间,而后出现加速度平台并维持一段时间,这是由于泡沫铝的压缩变形缓冲所致;当泡沫铝压缩硬化到一定程度,气缸的加速度瞬间发生二次突变;随着泡沫铝的回弹,应力程度的降低,气缸加速度由峰值迅速降低,并伴随着一定程度的振荡,经第三次突变达到稳定值。
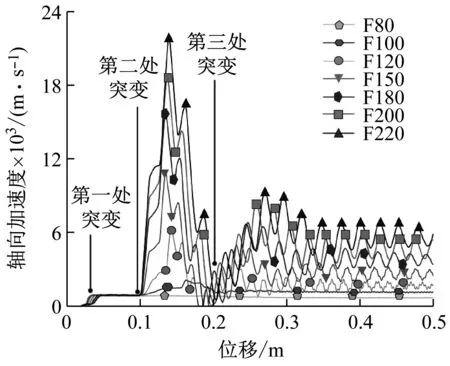
图7 加速度与位移关系Fig.7 Acceleration vs displacement
不同初速度入水瞬间产生的第一次加速度突变平台值基本一致,发生硬化产生二次加速度突变时的位移量相当;入水初速度越大,气缸的二次加速度峰值越大,且伴随的微幅振荡越明显,波峰衰减到波谷相伴的位移量越大。当速度达到一定程度,会从波谷产生第三次加速度抬升,此后维持稳定值,速度越大,稳定值越大。
铝合金空化器入水的加速度与位移耦合规律如图8所示。显然地,由于铝合金材质的刚度远大于泡沫铝材料,使得其加速度响应振幅过高,经过数个周期快速衰减到稳定值,伴随的位移量小于降载空化器。

图8 加速度与位移关系Fig.8 Acceleration vs Displacement
3.2 轴向力响应规律
图9对比了3组特征速度下(80 m/s,150 m/s,220 m/s)两种空化器入水的阻力遭遇情况,铝合金空化器与降载空化器质量相差4%。结果显示,相同初速度情况下铝合金空化器入水瞬间遭遇阻力的波峰宽度基本相当,峰值高于具有降载机构的空化器约14%,这是由于泡沫铝在冲击瞬间可以起到很好的缓冲作用。入水初速度越大,阻力峰值越大,稳定段阻力的振荡越明显。
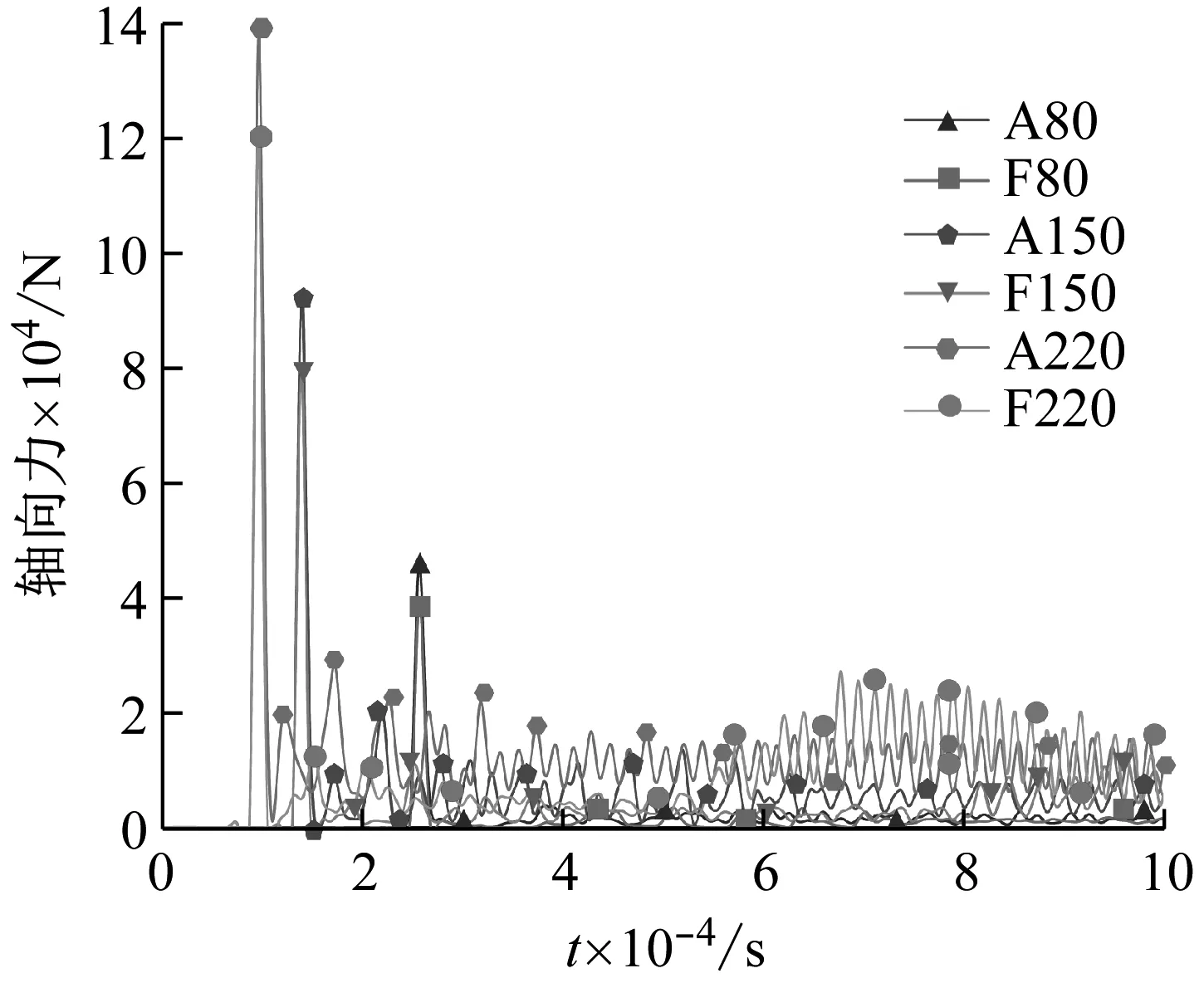
图9 轴向力响应Fig.9 Response of axial force
3.3 峰值与平稳值响应
如图10结果表明,降载空化器与铝合金空化器的轴向加速度幅值及轴向力幅值与入水速度呈正相关关系;随着速度的增大,二者轴向力幅值的增长率相当,而加速度幅值的增长率铝合金空化器大于降载空化器,具体响应统计数据见表5。
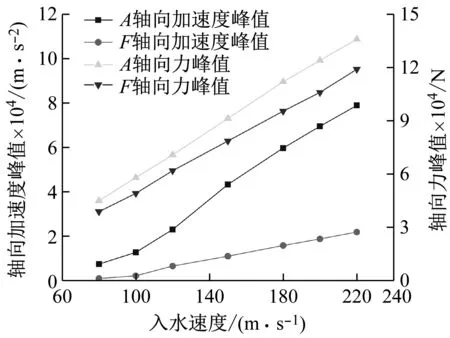
图10 结构响应峰值与入水速度关系Fig.10 Peak value of structure response vs water entry velocity
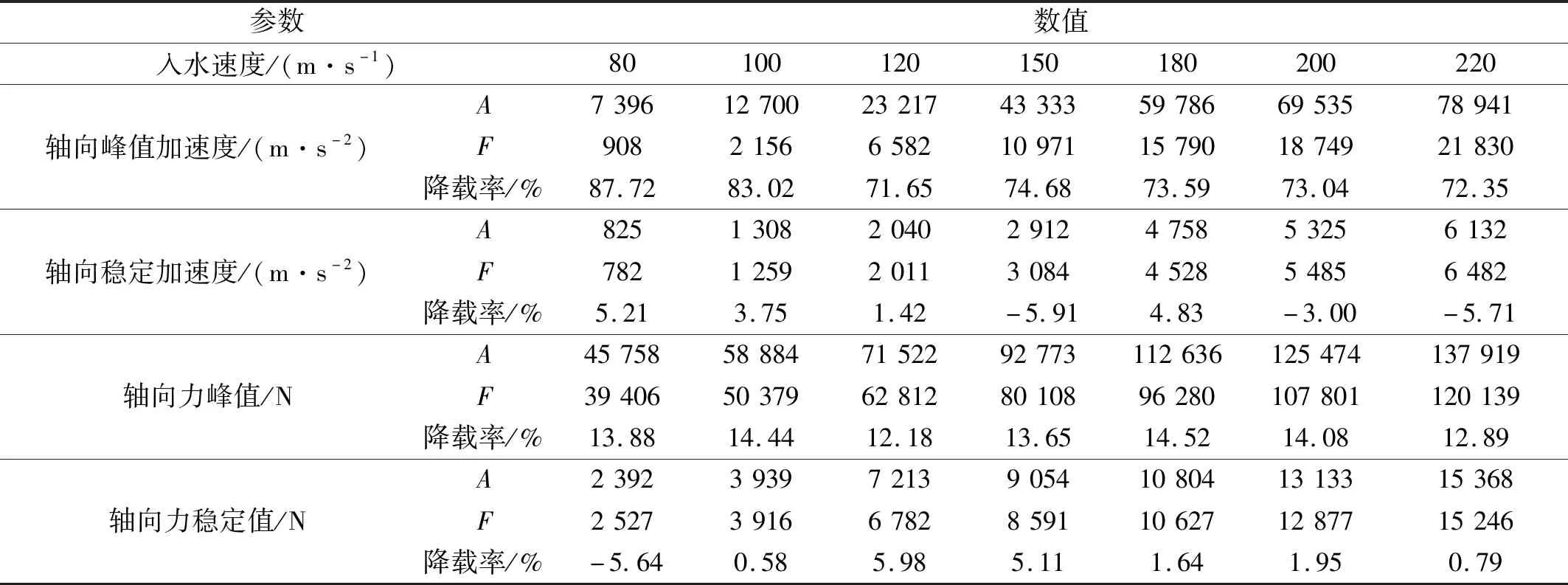
表5 响应参数统计Tab.5 Response parameter statistics
泡沫铝的应用对空化器入水降载十分显著,相较于铝合金空化器,能够有效降低轴向峰值加速度至少70%,轴向阻力峰值也略有降低;无论是加速度稳定值还是轴向力稳定值,二者基本相当,差值在±6%。
4 结 论
基于MSC.Dytran一般耦合方法的空化器垂直入水研究,结论如下:
(1)本文空化器构型在80~220 m/s的入水速度内,轴向加速度峰值及轴向力峰值与入水速度呈近似的线性正相关关系。
(2)泡沫铝的使用能够有效减缓空化器入水冲击的轴向加速度及轴向力的振荡,响应参数缓慢发展到峰值。
(3)泡沫铝对空化器入水降载十分显著,轴向加速度幅值降载率至少70%,轴向力幅值降载率可达14%;入水稳定段降载空化器与铝合金空化器的轴向加速及轴向力相当。

