地震作用下浮放物体运动状态研究
杨维国,胡卫中,齐 涛,刘 佩,王 萌,葛家琪
(1.北京交通大学 土木建筑工程学院,北京 100044;2.中国航空规划设计研究总院有限公司,北京 100120)
浮放物体指以浮放方式放置于基础平台上的物体[1],如文物、家具、仪器设备等。地震作用下,浮放物体通常会发生滑移、滑移-摇摆以及摇摆(倾覆)等运动方式,如图1所示。浮放物体一旦发生运动,容易发生损坏,产生不可估量的经济损失。浮放物体的运动状态是决定其保护措施的关键因素,如浮放文物通常采取鱼线固定法防止其摇摆(倾覆)。因此,为了更好的保护浮放物体,有必要针对浮放物体的运动状态及其运动规律展开研究。
国内外学者针对浮放物体的运动状态展开了大量研究。Housner[2]将浮放物体简化为块状刚体,建立了浮放物体的运动方程。Shi等[3]利用编制的计算机程序对不同宽高比矩形块体的摇摆响应进行了研究。Kounadis等[4-7]分别采用单刚体、双刚体以及三刚体模型对浮放物体的摇摆响应进行了推导分析。Shenton等[8-10]针对滑移、滑移-摇摆以及摇摆3种运动状态,推导了3种运动状态的动力学方程,并提出了进入不同运动状态的启动准则。Yang等[11]提出一种二维理论,对浮放物体在滑移、滑移-摇摆以及摇摆等运动状态下的动力响应进行了研究。Zhang等[12]通过对浮放物体的摇摆响应进行研究,提出物体的倾覆与基础激励的加速度峰值及频率有关。Taniguchi[13]对水平和竖向地震作用下浮放块体进行研究,发现浮放物体对摩擦因数和宽高比较为敏感。Pea等[14]对4种不同几何形状的花岗岩块体的摇摆响应进行了振动台试验研究,结果表明摇摆的幅度取决于载荷的频率和振幅。Konstantinidis等对浮放的冰箱进行了振动台试验研究,运动状态主要表现为滑移。周乾等[17-20]基于博物馆陈列展柜,并在展柜中浮放文物,对浮放文物的滑移和摇摆响应进行了振动台试验研究。Nezamisavojbolaghi等[21]将医院大型设备简化为质量偏心的浮放刚性块体,利用MATLAB程序对块体的摇摆响应进行了研究。
目前,研究多集中在浮放物体的摇摆响应,缺少针对滑移、滑移-摇摆以及摇摆(倾覆)3种运动状态的系统性研究,因此,本文将浮放物体简化为木制块体,围绕滑移、滑移-摇摆以及摇摆(倾覆)3种运动状态,采用试验与数值模拟相结合的研究方法,考虑宽高比、地震波的卓越频率、体型大小、形状以及质心高度等因素,对浮放物体的运动状态展开研究。

(a)
1 试验概况
1.1 试件设计
试件采用质地较硬的木材进行制作,共设计了9个试件,如图2所示。根据体型大小和形状分为A、B、C 3组,A、C组为长方体,C组体型大于A组,B组为圆柱体。初始设计宽高比分别为0.25、0.35、0.50。但由于试件加工过程导致试件尺寸偏差,试件宽高比与初始设计宽高比存在一定偏差,主要参数如表1所示。

表1 试件主要参数Tab.1 Main parameters of specimens

图2 试验试件Fig.2 Test specimens
1.2 试验设备
采用水平地震模拟振动台、倾角传感器以及加速度传感器等,如图3所示。振动台的台面尺寸为1 m×1 m,行程为±150 mm的运动范围,位移精度为0.02 mm。传感器量程为 ±180°,静态精度为0.05°,动态精度0.1°,质量为10 g。加速度传感器灵敏度为5 000 mV/g,量程为±10g,分辨率0.000 04g,质量为12 g。

(a)振动台
1.3 测量方案
倾角传感器和加速度传感器均布置在试件顶部,采用热熔胶固定,如图4所示。由于试件体积和质量较小,力学位移计会影响试件的运动状态,很难实现位移的动态测量,因此,采用记号笔在振动台面画出基准线,用于观察加载过程中的滑移情况。此外,对试验进行全程录像,结合加速度传感器和倾角传感器采集的动态数据,对试件的运动状态进行判别。

图4 传感器布置Fig.4 Sensor placement
1.4 地震波选取及荷载工况
选取6条卓越频率依次增大的地震波,以W1~W6进行编号,截取前30 s进行调幅作为振动台试验地震波输入,如表2所示。
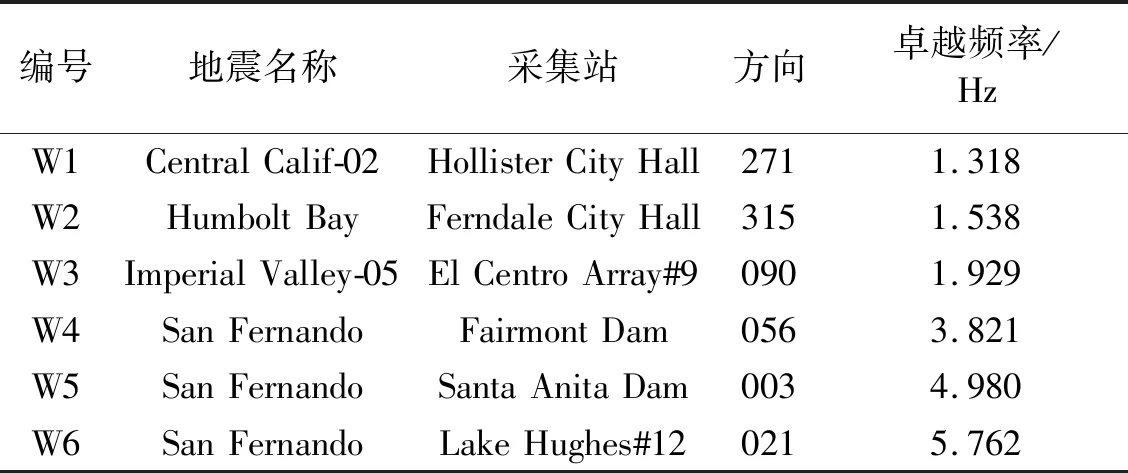
表2 所选取地震波的信息Tab.2 Information of selected seismic waves
首先,利用地震波W1、W2、W3分别对9个试件进行加载,每条地震波的加速度峰值逐级增加,分别取0.20g、0.25g、0.30g、0.35g、0.40g,当试件发生倾覆时,该条地震波的加速度峰值不再增加。然后,根据加载结果,选出发生滑移、滑移-摇摆和以及摇摆(倾覆)响应的典型试件C-7、A-2、C-9,采用地震波W1~W6进行加载,加载工况,如表3所示。

表3 荷载工况Tab.3 Load case
2 试验现象与破坏模式
2.1 摩擦因数测量
采用静拉试验进行动摩擦因数的测定,由于试验条件限制,假定静摩擦因数与动摩擦因数相等。将拉力计与振动台面保持平行,用鱼线和热熔胶将拉力计的拉钩与试件底部连接,使振动台面发生匀速水平运动,读取测力计示数,如图5所示,每个试件分别进行5次测量并取平均值,最终计算得到摩擦因数,如表4所示。

图5 测量摩擦因数Fig.5 Measuring friction coefficient

表4 摩擦因数Tab.4 Friction coefficient
2.2 试验结果
利用地震波W1、W2、W3分别对9个试件进行加载,试验发现,随着地震波加速度峰值的增大,试件的运动状态会发生改变,试件分别出现了滑移、滑移-摇摆以及摇摆(倾覆)3种运动状态,如表5所示。

表5 地震波W1~W3作用下试验结果Tab.5 Test results under the action of seismic wave W1-W3
对于宽高比接近0.5的试件,A-1、B-4、C-7的运动状态由静止转变为滑移。当地震波加速度峰值等于0.20g、0.25g、0.30g时,试件均处于静止状态,当加速度峰值由0.30g增大到0.35g时,试件开始滑移,当加速度峰值由0.35g增加到0.40g时,试件的滑移更为明显。
对于宽高比接近0.35的试件,A-2、C-8的运动状态由静止转变为滑移,再由滑移变为滑移摇摆,其中,地震波W3作用时,A-2由静止直接变为滑移摇摆。当加速度峰值0.25g增加到0.30g时,试件B-5的运动状态由静止转变为滑移-摇摆,在加速度峰值增加到0.40g时,出现倾覆现象。
对于宽高比接近0.25的试件,A-3、C-9的运动状态由静止转变为摇摆,再由摇摆转变为倾覆,当地震加速度峰值等于0.20g时,试件保持静止状态,当加速度峰值增大到0.25g时,试件变为摇摆,在加速度峰值增加到0.40g时,试件出现倾覆现象。试件B-6由于是圆柱体,在加速度峰值等于0.20g时就发生摇摆运动状态,随着加速度峰值增加,运动状态转变为倾覆。
综上所述,宽高比接近0.5的试件,长方体和圆柱体最终的运动状态均为滑移;宽高比接近0.35的试件,长方体最终为滑移摇摆,圆柱体最终为倾覆或滑移-摇摆,且出现滑移-摇摆的加速度峰值更小;宽高比接近0.25的试件,长方体和圆柱体最终的运动状态均为摇摆或倾覆,圆柱体出现摇摆的加速度峰值更小。由此可见,宽高比不同时,宽高比越大,试件越稳定,宽高比相同时,长方体试件比圆柱体试件更稳定。
为了研究地震波卓越频率对试件运动状态的影响,以滑移、滑移-摇摆和摇摆(倾覆)试件为研究对象,根据表5的试验结果,滑移状态选择试件C-7,加速度峰值0.40g,滑移摇摆状态选择A-2,加速度峰值取0.40g,摇摆状态选择试件C-9,加速度峰值取0.35g。采用地震波W1~W6对试件进行加载,结果如表6所示。从表6可以看出,对于滑移试件,随着地震波卓越频率的增加,试件的滑移程度减弱;对于滑移-摇摆试件,摇摆角度时程曲线见图6,摇摆角度依次为5.6°、4.3°、4.3°、3.5°、2.8°、2.2°;对于摇摆试件,摇摆角度时程曲线见图7,由图和表可知,地震波W1~W2作用下,试件发生倾覆,而在地震波W3~W6作用下,试件发生摇摆,最大摇摆角度分别为10.1°、5.5°、3.8°、3.3°。由此可见,试件的运动响应随地震波卓越频率的增大而减弱。

表6 地震波W1~W6作用下试验结果Tab.6 Test results under the action of seismic wave W1-W6

(a)地震波W1~W3作用
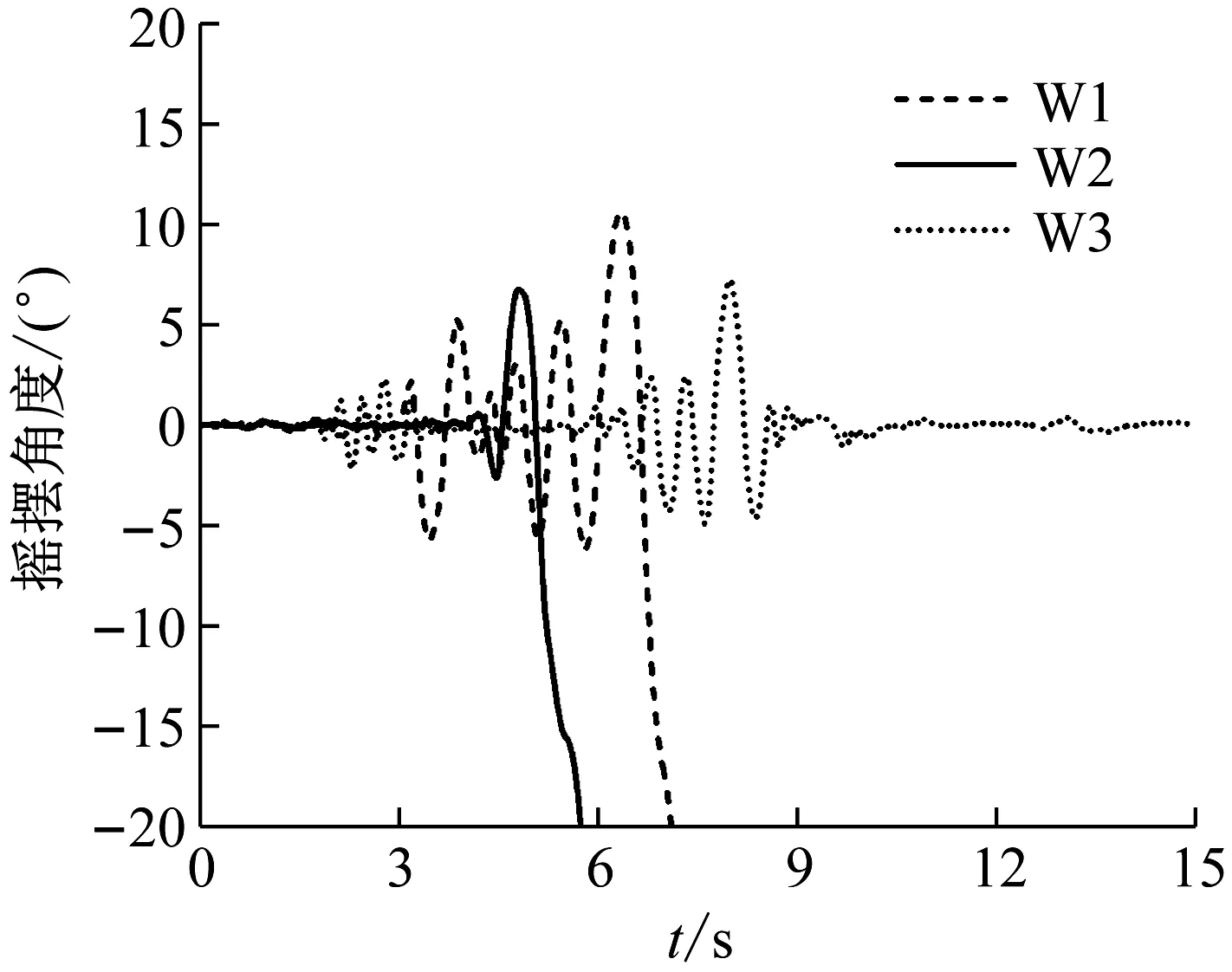
(a)地震波W1~W3作用
3 有限元模型验证
利用ABAQUS软件建立有限元模型,包括振动台面和试件。台面采用钢材,密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3,在中心创建参考点RP-1,以此点为约束控制点建立刚体约束将台面约束,使其等效为刚体。试件材料与试验木材保持一致,密度按照每个试件的实际密度进行输入,弹性模量为13 GPa,泊松比为0.4。试件底面与振动台面采用面面接触,切向采用罚摩擦,摩擦因数与试验一致,法向采用硬接触,允许接触后分离,由于试件会发生倾覆,试件侧面与台面也设置接触。
为了得到摇摆角度,在试件质心处建立参考点RP-2,以此点为约束控制点建立刚体约束,使试件各点自由度与质心相同且各点之间无相对位移。滑移采用试件底面中心点与底板中心点的相对位移。单元采用八节点六面体单元C3D8R,有限元模型,如图8所示。

图8 有限元模型Fig.8 Finite element model
为了保证有限元模型的有效性,分别选取滑移、滑移-摇摆以及摇摆倾覆3种运动状态的试件,并以不同的地震波进行输入。
滑移运动状态选择试件C-7,地震波W1,加速度峰值为0.35g,由于试验过程中未能获得试件的位移时程曲线,因此采用加速度时程曲线进行对比,如图9所示。可见有限元与试验的曲线拟合较好。滑移-摇摆运动状态选择试件A-2,地震波W4,加速度峰值为0.40g,摇摆角时程曲线与试验曲线拟合较好,如图10所示。有限元结果显示试件A-2发生滑移-摇摆运动,与试验结果一致。摇摆运动状态选择试件C-9,地震波W2,加速度峰值为0.30g,摇摆角时程曲线与试验曲线拟合较好,如图11所示。有限元结果显示试件C-9发生摇摆运动,与试验结果一致。由此可见,建立的有限元模型具有较好的有效性。

图9 试件C-7加速度时程对比图Fig.9 Acceleration time history comparison diagram of specimen C-7

图10 试件A-2摇摆角度时程对比图Fig.10 Time history comparison diagram of rocking angle of specimen A-2
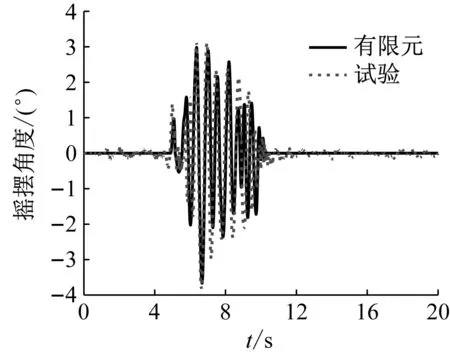
图11 试件C-9摇摆角度时程对比图Fig.11 Time history comparison diagram of rocking angle of specimen C-9
4 参数分析
利用验证后的数值模型,围绕滑移、滑移-摇摆以及摇摆(倾覆)3种运动状态,以地震波卓越频率、体型大小以及质心高度为参数,对浮放物体的最大滑移量和最大摇摆角度进行了研究,分析其变化规律。经过试算并结合试验结果,确定有限元参数分析的基本试件:对于滑移试件,宽高比取为0.8,峰值加速度取为0.6g,试件尺寸为100 mm×100 mm×125 mm;对于滑移-摇摆试件,宽高比取0.33,峰值加速度等于0.45g,试件尺寸为100 mm×100 mm×300 mm;对于摇摆(倾覆)试件,宽高比取0.25,峰值加速度等于0.35g,试件尺寸为100 mm×100 mm×400 mm。
4.1 地震波卓越频率的影响
采用地震波W1、W3、W4、W5、W6对基本试件进行加载,卓越频率依次为1.318 Hz、1.929 Hz、3.821 Hz、4.980 Hz、5.762 Hz,结果如表7所示。从表中可以看出,当地震波卓越频率增大时,对于滑移试件,最大滑移量呈减小趋势;对于滑移-摇摆试件,最大滑移量的影响无明显规律,最大摇摆角度减小;对于摇摆试件,最大摇摆角度减小。
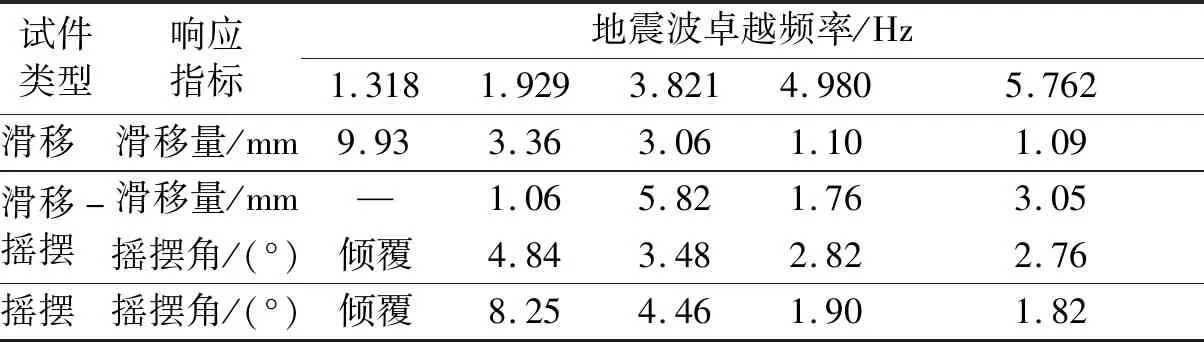
表7 卓越频率影响Tab.7 Influence of predominant frequency
4.2 体型的影响
为了研究体型变化的影响,在基本试件的基础上,保持宽高比不变,将底面边长分别取为5 mm、10 mm、15 mm、20 mm、25 mm。输入采用Elcentro波、TAFT波以及Elcentro-16 m波[22],Elcentro-16 m波是某博物馆16 m处的楼层波时程,以考虑浮放物体置于楼层内情况,加载结果如表8所示。从表中可以看出,当体型增大时,对于滑移试件,滑移量基本不受影响;对于滑移-摇摆试件,滑移量的变化无明显规律,摇摆角度减小;对于摇摆试件,摇摆角度减小。

表8 体型的影响Tab.8 Influence of body size
4.3 质心高度影响
对于容易发生倾覆的瘦高型浮放物体,通常采用降低重心法来增加稳定性,为了研究其变化规律,本文以摇摆(倾覆)试件为研究对象,将试件的质心高度分别取为110 mm、140 mm、170 mm、200 mm、230 mm,分别采用Elcentro波、TAFT波以及Elcentro-16 m波进行加载,结果如表9所示。由表可知,随着质心高度的降低,浮放物体的稳定性增加,使倾覆运动状态转变为摇摆运动状态,使摇摆运动状态的摇摆角度减小。

表9 质心高度的影响Tab.9 Influence of centroid height
5 结 论
本文以浮放物体为研究对象,将浮放物体简化为木制块体,通过振动台试验与数值模拟相结合的研究方法,对浮放物体的运动状态进行了研究,主要结论如下:
(1)浮放物体的宽高比不同时,宽高比越大,试件越稳定,而宽高比相同时,长方体试件比圆柱体试件更稳定。
(2)浮放物体的运动响应随地震波卓越频率的增大而减弱。当地震波卓越频率增大时,对于滑移试件,最大滑移量呈减小趋势,而对于滑移-摇摆试件,最大滑移量无明显变化规律;对于滑移-摇摆和摇摆试件,最大摇摆角度随卓越频率的增大而减小。
(3)体型的变化对浮放物体的最大滑移量无影响,对最大摇摆角度影响明显,摇摆角随着体型的增大而减小。
(4)降低质心高度能够增加浮放物体的稳定性,能够将浮放物体的运动状态由倾覆减弱至不再激起摇摆,可有效保护浮放物体。
(5)有限元计算结果与试件结果拟合较好,可有效模拟浮放物体在水平地震作用下的滑移、滑移-摇摆以及摇摆(倾覆)响应。

