基于数据驱动的叶片加工质量评估方法研究*

吴国新 潘 涛 刘秀丽 徐小力

(北京信息科技大学现代测控技术教育部重点实验室，北京 100192 )

叶片是航空发动机的关键零件，具有种类多、数量大、结构复杂和几何精度要求较高、加工难度大等特点[1-2]。它的加工质量，几何精度直接关系着发动机的性能，并影响着航空器的安全性；其型面参数的质量密切影响着发动机的气动性能[3]。近年来，随着国家对航空航天事业的投入不断加大以及各种高性能发动机的研制，航空器零件的生产规模不断扩大，叶片的需求和产量大增[4]。对叶片进行检测时，大多采用三坐标测量机分别对不同的若干个截面采集点云数据，再根据软件算法评价出单截面内各个参数的数据，最后进行汇总分析[5-8]。分析测量数据时，目前仍沿用人工拿实测值和标准值进行比对、筛选数据并判断合格性的方法，存在效率低、主观性强等问题。利用此方法得出的数据能够判断某个截面的某个参数是否符合标准，但是不能有效分析各个参数之间的关系。在对叶片的加工质量分析时，发现会有诸多原因造成误差，如加工原理误差、装夹误差及工艺系统几何误差等等[9]，结合制造加工时的误差原因分析，可为叶片生产制造中提高叶片生产精度提高参考。因此，对叶片型面的快速检测和分析对提高叶片检测效率，挖掘参数之间的相互关系及影响因素，保障叶片加工质量具有重要意义。

本文采用多元线性回归方法，选取同一叶盘上27个叶片作为研究对象，分别对相同截面的17个质量检测点用三坐标测量机进行测量。分析数据之间的内在联系，为叶片制造部门提高叶片制造精度提供参考。

1 数据与方法

1.1 数据来源与预处理

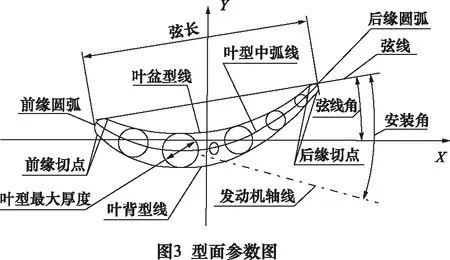
以某型号叶盘上的27个叶片的测量为例，测量示意图如图1所示，用实验室接触式三坐标测量机分别对这27个叶片的型面参数进行测量。具体方法为选取某一叶片底座为基准面，分别定义多个高度，选取若干个截面(如图2所示)，用测量机对这些截面的若干参数进行评定，测量过程均在20±0.5 ℃、54%RH环境下进行。常用的截面参数图如图3所示。

其中，测量参数有厚度、弦长和轮廓度等17种，全部测量参数见表1。

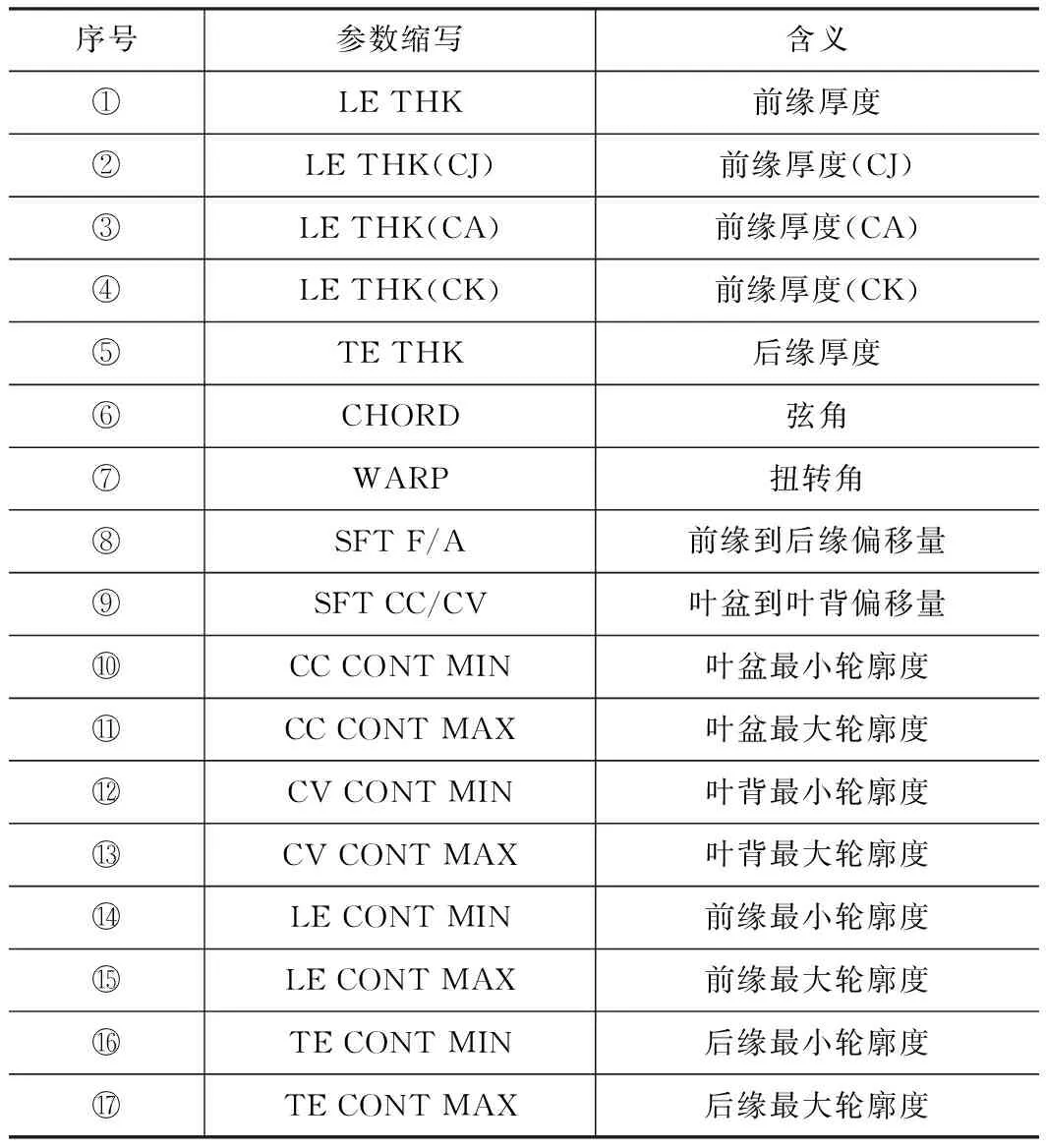
表1 测量参数表

当完成所有测量时，结合设计部门给出的理论值和公差，计算出差值。通过该差值与公差比较判断数据是否在公差带内，若超过公差带，则判定数据不合格，不予考虑。

1.2 多元线性回归理论

线性回归(linear regression)[10-12]是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。回归分析是从一组数据出发通过一个或一些变量的变化解释另一个变量的变化，主要研究的是变量之间的统计关系。

多元线性回归的基本模型为：

y=β0+β1x1+β2x2+…+βkxk

(1)

式中:x1，x2，…，xk是自变量;y是因变量;β0，β1，…，βk是未知参数，也称为回归系数;k是影响因素的个数。常采用最小二乘法对上述方程的未知参数β0，β1，…，βk进行估计，分别求得系数值。

最后，对回归模型进行显著性检验，构造F检验统计量对总体进行显著性检验，通过Q-Q图法[13-14]分析残差值，判断其是否符合正态分布。

1.3方法

在用最小二乘法求解式(1)系数时，我们可以将表达式y向量化，即将y表示为两个向量相乘的形式，则有以下表述：

(2)

β=(β0,β1,…,βk)T

(3)

令：

(4)

则有：

(5)

判定系数R2的表达式为：

(6)

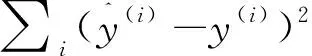
=(Xbβ-Y)T·(Xbβ-Y)

(7)

令：

(8)

解得：

(9)

至此得到式(1)的系数求解原理，然后对17种参数分别取一种参数值作为因变量y，其余16种参数作为自变量x，选择多元线性回归模型y=β0+β1x1+β2x2+…+β16x16，做回归过程17次，即：

(10)

利用最小二乘法对方程组(10)进行求解，利用MATLAB软件实现多元线性回归方程的拟合和分析。

2 数据分析

2.1 数据预处理

选取某一截面，分析测量值与理论值的差是否在公差带范围内，即：

Deviation=Actual-Nominal

(11)

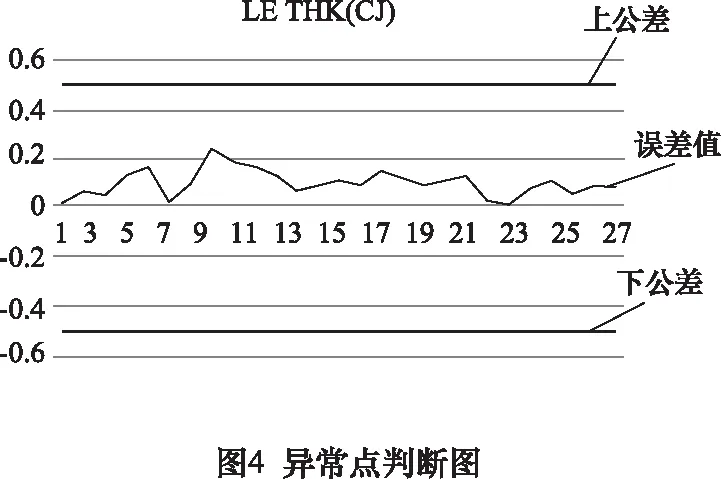
分别对27个叶片的17个参数的测量数据的误差作点图，判断各个参数的27个误差值是否在允许的公差带范围以内，若出现某点在公差带外，则表明该点所对应的叶片的所测截面的参数不合格。以LE THK(CJ)为例，如图4所示，发现THK(CJ)参数里并未发现异常点。

2.2 求解系数

采用公式(1)的回归模型，以第17个参数TE CONT MAX的误差数据的绝对值为y值为例，其余16个参数的误差数据分别为x1～x16值，通过MATLAB软件进行线性回归分析，得到回归系数，如表2所示。

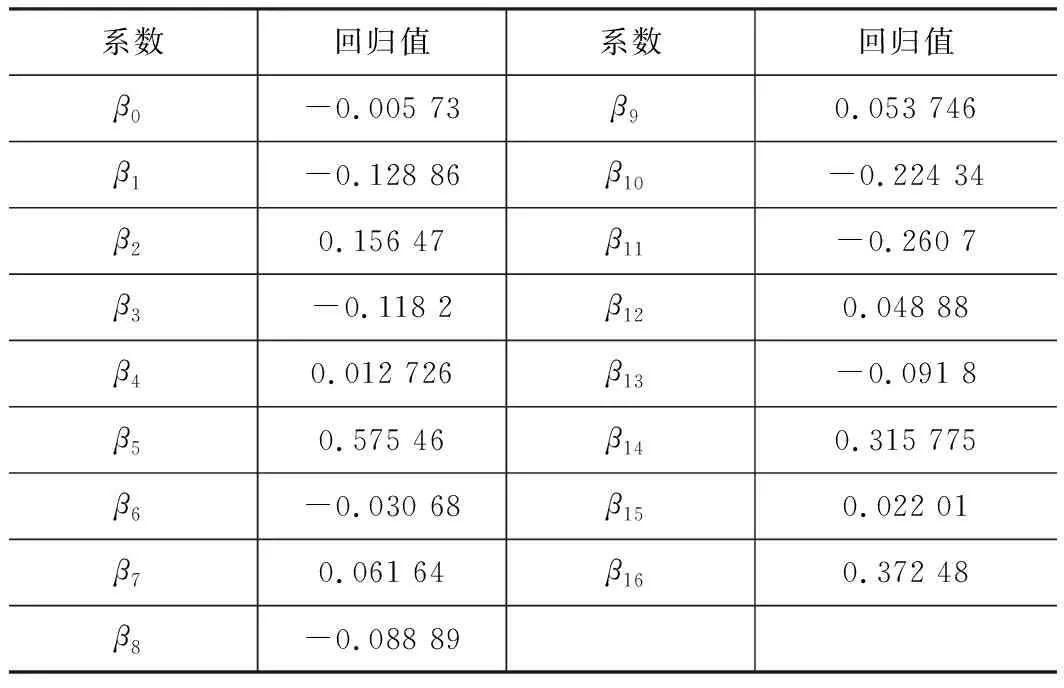
表2 参数TE CONT MAX的回归系数表

2.3 检验结果分析

判定系数R2是判断回归模型拟合程度的一个指标，其取值范围为[0,1]，数值越大说明回归模型拟合程度越高；F值为总模型的F测验值，F越大说明回归方程越显著；F统计量概率值P若小于α(默认5%)，则回归模型成立。

通过表3能清晰地得知被选数据的拟合情况，结果显示，判定系数R2=0.966 238 8，表明拟合度较好；P=0.000 0480.05，表明TE CONT MAX的误差值与其他16个参数的误差值得整体线性关系是显著的。

表3 参数TE CONT MAX的Stats值

2.4 最优模型选择

通过以上方法，分别以第一个参数LE THK至第16个参数TE CONT MIN作为y值，剩余16组参数误差值作为x1～x16值作线性回归，得出以下结论：

首先，当以WARP、SFT F/A、SFT CC/CV等3个参数的误差值作为y值时，P值大于α(0.05)，回归模型不成立，故不作考虑。

其次，当以LE THK(CK)、CHORD、CV CONT MIN、CC CONT MIN、LE CONT MIN、LE CONT MAX、TE CONT MIN等5个参数的误差值作为y值时，它们的F值偏小(在1～5范围内)，不具参考意义，故不作考虑。剩余7组Stats值如表4所示。

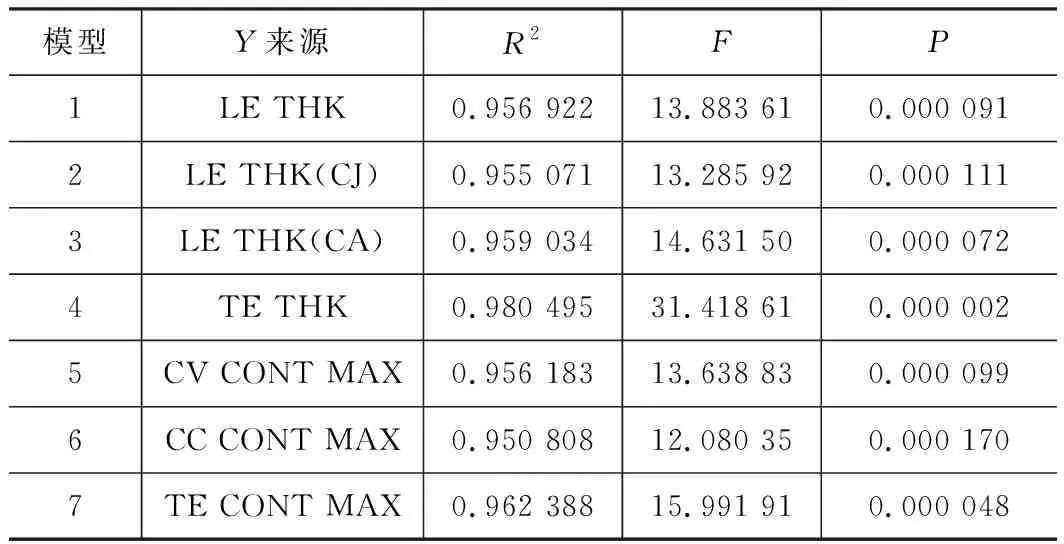
表4 各模型的Stats值

由表4综合分析R2、F、P值，发现模型4为最优模型，即以TE THK的误差值作为y，其余16个参数的误差值分别为x1～x16值的线性回归模型，其回归系数如表5所示。

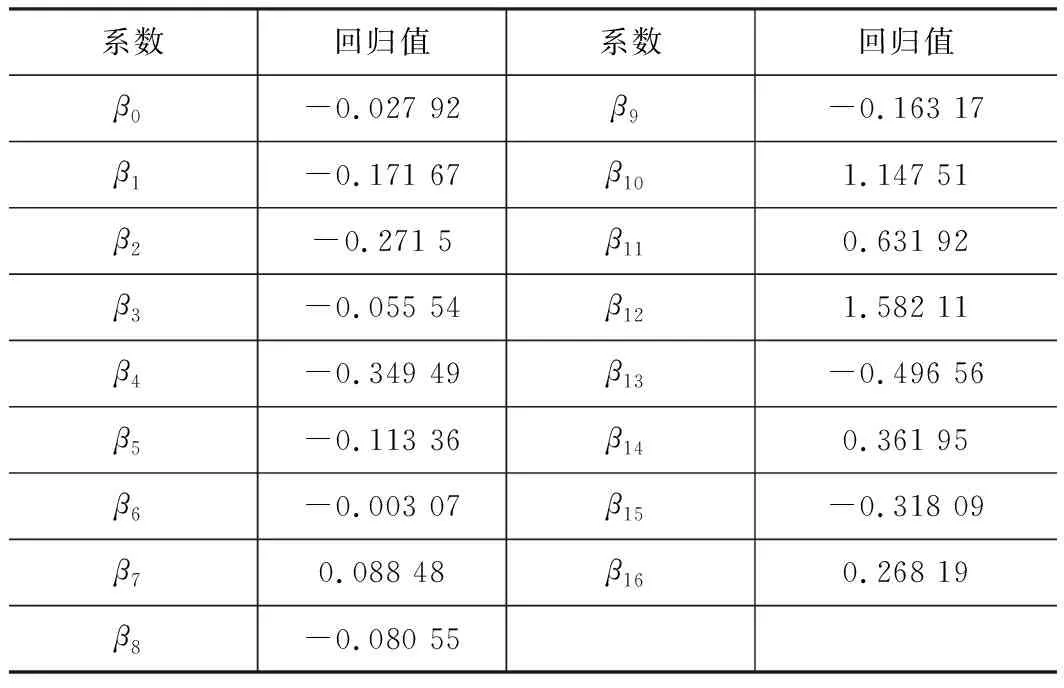
表5 最优模型回归系数表

由表5中的系数可知，参数TE THK的误差值与CV CONT MAX、CC CONT MAX的误差值之间有较强的线性关系，与LE THK(CA)、WARP、SFT F/A、SFT CC/CV线性关系最小，与其他参数的误差值线性关系一般。

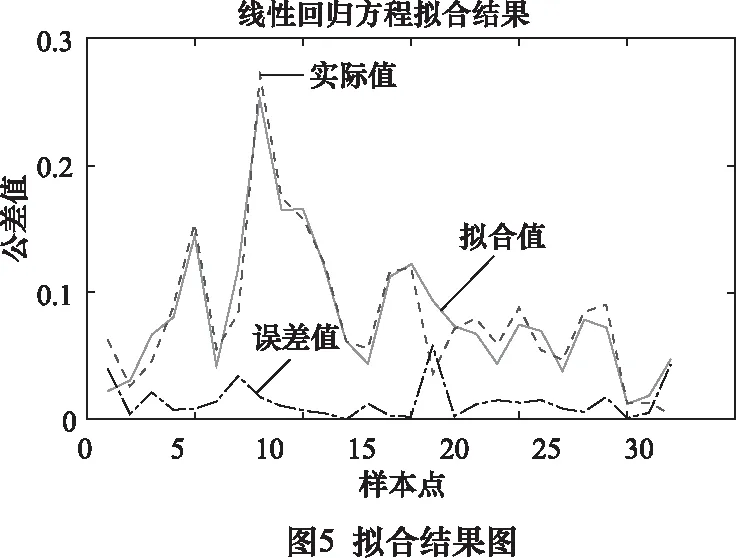
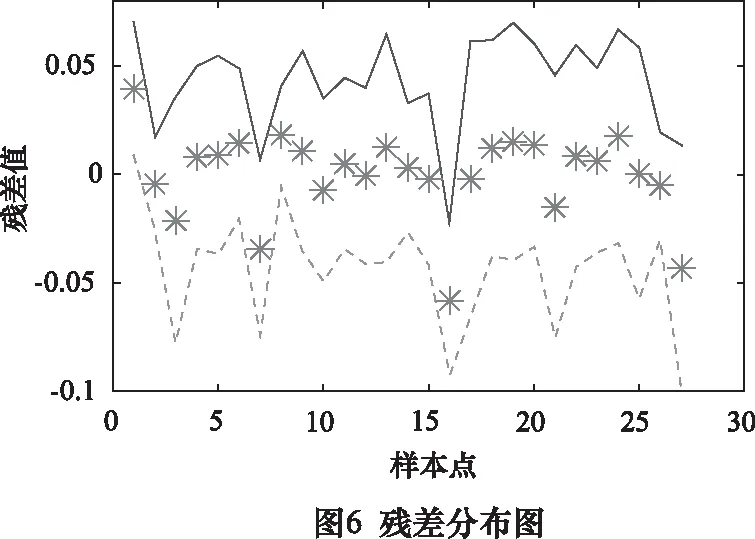
线性回归拟合结果图如图5所示，发现误差值均小于0.05。残差分布图如图6所示，发现残差值均位于其置信区间内。

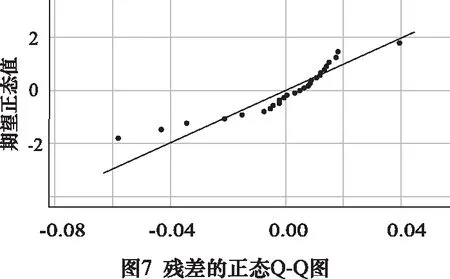
最后用SPSS软件分析残差数据判断是否符合正态分布：残差值的正态Q-Q图如图7所示，发现点子落在近似落在一条直线附近，则表明残差值近似为正态分布，其中斜率为标准差，截距为均值。因此可认为残差是随机产生的，拟合效果不依赖于某些特殊的值，以上回归模型可接受。

3 结语

本文主要选取了某一叶盘上的27个叶片的测量数据，通过三坐标测量机采用截面测量的方法，测量了17组参数的数据，并根据理论值得出误差，找出了一组基于参数误差值的最优的线性方程，分析了各个参数之间的误差线性关系。

通过分析参数之间的数据模型关系，能够对叶片加工工艺与制造过程的优化给予参考和指导，为叶片生产制造部门提高叶片生产精度提高参考。