电动伺服机构三闭环控制器设计

董海迪，王 哲，袁胜智，李 静，金 凯

（海军工程大学兵器工程学院，湖北武汉 430030）

舵机伺服系统是一种复杂的机电一体化系统，属于典型的位置随动系统［1］。其控制精度直接影响导弹的制导和姿态控制精度，进而影响导弹命中精度。

针对某型导弹现有电液伺服系统存在动态响应速度慢、结构复杂、可靠性差、使用维护困难等缺点［2］，本文研究了采用直流电机进行电动舵机设计的改进方案，在分析舵机控制系统组成及工作原理基础上，依据电磁定律等物理规律推导建立舵机控制系统数学模型。针对某导弹电动舵机控制系统的性能指标要求，提出一种基于工程经验的PID 控制算法，进行电流、速度、位置三闭环调节器设计。 最后，利用Matlab/Simulink工具箱搭建电动舵机控制系统的仿真模型。

1 舵机控制系统数学模型

舵机控制系统主要由伺服电机、主功率驱动电路、减速传动机构以及电机工作电流、转子转速、喷管偏角等检测传感器组成，具体结构如图1所示。

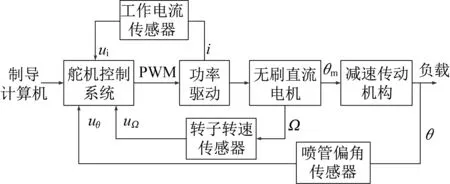
图1 舵机控制系统组成结构Fig.1 Composition of servo control system

1.1 无刷直流电机数学模型

无刷直流电机是在传统的有刷直流电机的基础上发展起来的，两者结构相似。不同之处在于，无刷直流电机把永磁体安装在转子上，三相绕组安装在定子上，利用逆变器和转子位置传感器构成电子换相电路，取代了原来由换相器和电刷组成的机械结构。无刷直流电机主要由电机本体、转子位置传感器和电子开关电路三部分组成。本文以两极三相无刷直流电机为例，推导建立无刷直流电机的数学模型，所建立的无刷直流电机动态结构如图2所示。

图2 无刷直流电机动态结构图Fig.2 Dynamic structure diagram of brushless DC motor

无刷直流电机相电压方程［3］为

无刷直流电机的传递函数为

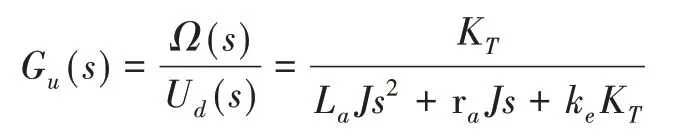
负载转矩与速度间的传递函数为

1.2 驱动器数学模型

驱动器主要由功率驱动管和三相逆变桥组成，分析时，常常将它们作为一个小环节处理［4］。输入量为PWM 输入电压，输出量为加在电机上的直流平均电压，同时考虑功率开关管存在滞后现象，故PWM 驱动器传递函数为

1.3 减速传动机构数学模型

减速器选用滚珠丝杠减速传动机构，其物理基础是滚动摩擦，由于依靠的是滚动摩擦，所以摩擦力较小，系统传动效率较高。减速传动器正常工作时，滚珠丝杠每旋转一周，带动螺母移动一个导程，推动喷管转动一定角度。若电机转动的角度为θm，则喷管转动的角度为

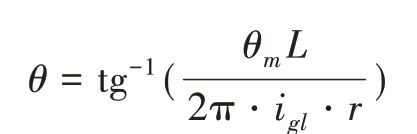
式中，θ表示喷管转动角度，L表示滚珠丝杠的导程，igl表示减速齿轮的减速传动比，r表示喷管转动半径。

由于θ最大幅值在10°左右，tg10°= 0.176，10°=，因此，在θ取值较小时，。减速传动机构传递函数为

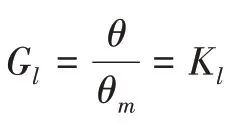
1.4 传感器数学模型

控制系统采用电流、速度、位置三闭环控制策略，涉及电机工作电流、转子转速及喷管偏角的测量反馈。其中电流测量采用霍尔传感器，输出与被测电流成比例的电压信号；转子转速测量采用与转轴同轴安装的旋转变压器，输出与转速成正比的数字信号；喷管位置检测采用与滚珠丝杠同轴安装的绝对值编码器，输出可以换算成与偏角成比例的数字信号。综上分析，三类传感器都可以等效为比例环节。考虑在电机工作过程中，三个检测信号中存在交流干扰，因此，在数据处理时，设计了数字滤波环节，滤波环节延迟了反馈信号的作用，可以等效为一阶惯性环节［5］。电流、转速、偏角三个传感器的传递函数数学模型分别为

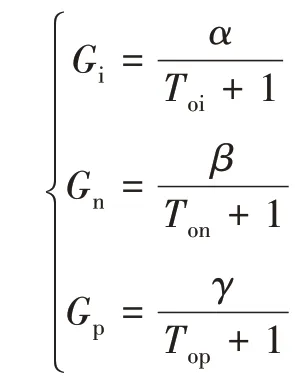
式中，α、β、γ分别表示电流、转速、偏角位移传感器比例系数，Toi、Ton、Top分别表示过滤时间常数。

2 舵机控制器设计

根据前文推导的各组成部分数学模型，得到控制系统动态结构如图3 所示。考虑到PID 控制具有算法简单、鲁棒性好、易于实现等优点［6］，尤其适用于建立精确数学模型的控制系统，因此，本文拟采用PID 控制算法设计三闭环控制器。基本思路是：首先进行电流环设计，通过对控制对象传递函数和控制性能指标分析，完成电流环调节器的结构和控制参数选择；然后将电流环等效为速度环的子环节，进行速度环设计；最后将速度环等效为位置环的子环节，进行位置环设计。

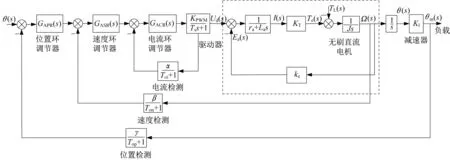
图3 控制系统动态结构图Fig.3 Dynamic Structure Diagram of Control System

2.1 电流环调节器设计

电流环调节器设计需要考虑结构和控制参数两方面。在输入信号中加入滤波时间常数与反馈滤波时间常数相同的滤波环节，并将其等效移动到电流环内，忽略反电势的变化影响［5］，同时考虑到滤波时间常数Toi和PWM 控制时间常数Ts比电气时间常数Tl小得多，在进行工程设计时，完全可以将两者当作小惯性群环节而近似作为一个惯性环节来处理，对应的时间常数T∑i=Ts+Toi。经简化处理得到电流环的开环传递函数为

电流环的控制对象是双惯性型的，控制的稳态要求是无静差，动态要求是迅速跟踪期望的电流变化，且不允许有太大的超调，因此电流环采用典型Ⅰ型系统进行校正［5］，电流环调节器采用PI调节器进行设计，对应的传递函数为

式中，Ki表示比例系数，τi表示超前时间常数。

选择电流环调节器的零点，使其能够与开环传递函数较大的时间常数进行极点对消，对应的积分时间常数τi=Tl，则电流环开环传递函数为

式中，KI=αKPWMKi/(Raτi)，表示开环放大系数。

为了控制电流的超调量在5% 以内，选择KIT∑i=0.5。PWM 开关频率为50 KHz，则Ts= 0.00002 s，KPWM取0. 85，Toi取0. 0001 s，T∑i=Ts+Toi= 0.00012 s，α暂取为1。电机定子电阻R= 0.044 Ω，定子电感L-M=25 mH，则Tl=La/Ra= 0.0057 s。电流环调节器参数为，Ki= 2.46，τi= 0.0057 s。电流环开环截止频率为

使用MATLAB 中的Bode 函数绘制电流环调节器加入前后的电流环开环频率响应曲线，如图4 所示。系统在进行校正前，电流环开环传递函数的截止频率为2010rad/sec，对应的相角裕度为78°，此时相角裕度过高，需要增大开环截止频率，减小相角裕度，提高电流环的动态响应速度；加入电流环调节器后，电流环开环传递函数的截止频率为4030rad/sec，相角裕度为59°。工程设计中一般要求将系统的相角裕度控制在45°左右，因此需要对PI调节器的控制参数进行反复调整，最终选择电流环调节器最优的控制参数KI为5. 32，得到电流环开环传递函数的截止频率为6380rad/sec，对应的相角裕度为46°，完全满足系统的稳定性和快速性要求。

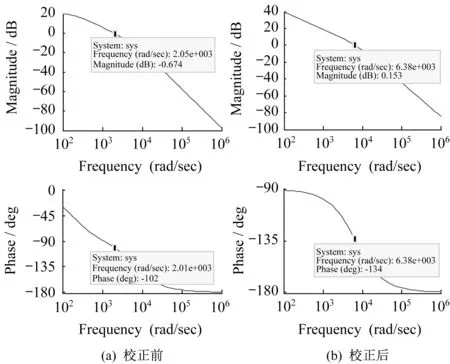
图4 电流环校正前后Bode图Fig.4 Bode diagram before and after current loop correction

2.2 速度环调节器设计

速度环对于系统受到的大负载扰动、位置控制精度以及系统低速时的平稳性等作用非常明显，其精确设计是保证舵机伺服系统较好地控制性能的关键环节［8］。电流环经简化处理后可作为速度环的一个子环节，将时间常数为Tl和Ton的两个小惯性环节合并为一个惯性环节，时间常数T∑n=Tl+Ton，则在空载条件下，速度环控制对象的开环传递函数可以简化为

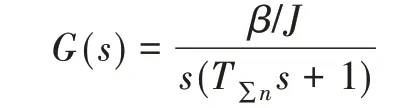
根据调速系统在稳态时无静差和在动态时应有较好的抗扰动性能的要求，速度环按典型Ⅱ型系统校正［5］。速度环的被控对象由一个积分环节和一个小惯性环节组成，因此速度环采用PI 调节器，对应的传递函数为

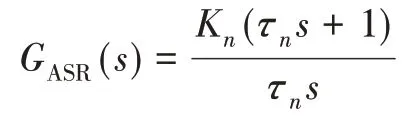
式中，Kn表示比例系数，τn表示超前时间常数。

速度环经过校正后，得到的开环传递函数为

式中，KN=βKn/(τn·J)，表示开环放大系数。

依据震荡指标最小的准则［5］，选择调节器的控制参数，速度环的开环增益为

式中，h表示控制系统中频段的宽度，其数值大小能够直接影响到系统的调节时间和扰动恢复时间等动态性能［5］，工程设计中h一般取值为4-5 效果较好，本系统中h取5。

Ton取 0. 001 s，T∑n=Ton+Tl=Ton+ 2T∑i=0.00124 s，J= 0.00362 kg × m2，β暂取1。则速度环调节器参数为τn=hT∑n= 0.0062 s，78043.7，Kn=KNτnJ/β= 1.75，截止频率ωcn=KNτn=483.87。

使用MATLAB 中的Bode 函数，绘制速度环调节器加入前后的速度环开环频率响应曲线，如图5 所示。在没有加入校正环节时，得到的速度环开环传递函数的截止频率为240rad/sec，对应的相角裕度为73°，此时控制系统不能够满足系统较高的稳态和较快的响应速度的要求；调整后的速度环开环传递函数的截止频率为404rad/sec，对应的相角裕度为42°，此时的控制系统能够满足系统较高的稳定性和较快的响应速度的要求。

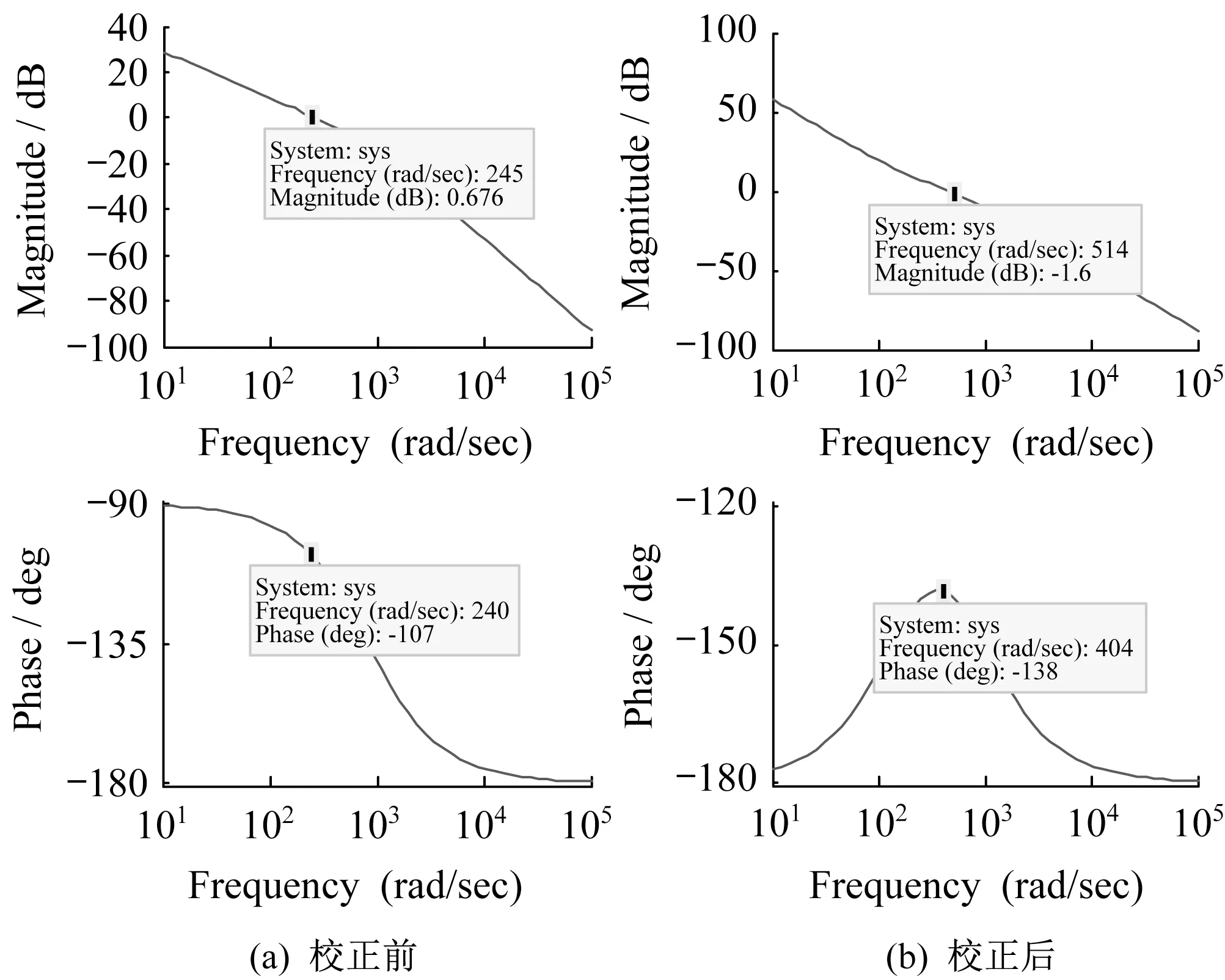
图5 速度环校正前后Bode图Fig.5 Bode diagram before and after speed loop correction

2.3 位置环调节器设计

速度环经简化处理后可作为位置环的一个环节，将时间常数为Top、τn和T∑n三个小惯性环节合并为一个惯性环节，时间常数T∑p=Top+τn+T∑n，则位置环控制对象的开环传递函数可以简化为

位置环控制系统设计的基本要求是在保证系统无超调量的前提下，响应速度尽可能快，因此按照典型Ⅰ型系统对位置环控制系统进行校正［5］。本文采用P 调节器对位置环控制系统进行设计，对应的传递函数为

式中，KP表示比例系数。

控制系统经过校正后，得到位置环的开环传递函数为

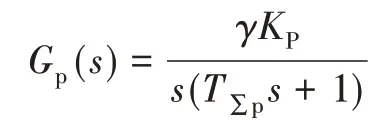
为了控制电流的超调量在5% 以内，这里取γKPT∑p= 0.5，Top= 0.01s，τn= 0.0062 s，T∑n=0.00124 s，则T∑p= 0.01744 s，T∑n= 0.00124 s，r 暂 取1。位置环调节参数为KP= 28.67，开环截止频率为ωcp=KP= 28.67 Hz。

使用MATLAB 中的Bode 函数绘制位置环调节器加入前后的位置环开环频率响应曲线，如图6 所示。控制系统在加入位置环调节器之前，开环传递函数的截止频率为1. 15rad/sec，对应的相角裕度接近90°，因此位置环无法保持稳定；加入校正环节后得到的开环传递函数截止频率为27. 2rad/sec，对应的相角裕度为75°，位置环的稳态性能和动态响应性能有待提高。因此将位置环比例系数KP调整到56，此时位置环的截止频率为49. 5rad/sec，对应的相角裕度为48°，控制系统的稳态性能和动态响应性能都比较满意。

图6 位置环校正前后Bode图Fig.6 Bode diagram before and after position loop correction

3 仿真验证

在完成控制系统建模和控制器设计后，采用模块化设计方法在Matlab/Simulink平台上设计系统仿真模型［9］，具体如图7 所示，主要包括无刷直流电机本体、转子逻辑换相、三相逆变桥驱动和舵机控制器四个模块。参照实际伺服电机性能参数设定电机仿真参数，从系统快速响应性能和跟踪特性两方面进行仿真实验［10］，其中负载设计为随角度增大而增大的弹性负载。

图7 控制系统仿真模型Fig.7 Control system simulation model

3.1 快速性能测试

为了测试舵机控制系统的动态响应性能和稳态精度，施加幅值为±10°的阶跃信号，测量得到系统响应输出的仿真结果如图8 所示。由图8 可知，系统在＋10°阶跃信号激励下的上升时间为12. 2 ms，调节时间为18. 3 ms，超调量为1. 2%；－10°阶跃信号激励下的上升时间为12. 2 ms，调节时间为18. 3 ms，超调量为1. 2%，满足舵机伺服系统设计的动态响应性能指标要求。

图8 阶跃信号响应仿真曲线Fig.8 Step signal response simulation curve

3.2 跟随性能测试

为了测试舵机控制系统的跟踪性能，分别施加幅值为2°、5°以及频率为1 Hz、2 Hz 和5 Hz 的正弦波信号。系统在不同正弦激励信号下的仿真结果如表1 所示。由表1 可知，随着激励信号频率增大，系统响应输出幅值减小、相移增大、跟踪误差增大；随着激励信号幅值增大，系统相移增大、跟踪误差增大。

表1 跟随性能仿真结果Tab.1 Simulation results of follow performance

4 结语

本文提出了一种基于工程经验的PID 设计方法，完成了电动舵机系统控制器设计，给出了电流、速度、位置三闭环调节器结构和控制参数选择依据，最后利用Matlab/Simulink 工具箱搭建系统仿真模型，设计了控制系统快速响应性能和跟随特性实验，仿真结果表明，本文所建立的数学模型能够准确描述舵机控制系统，控制器稳态精度和响应速度指标均达到设计要求。