直齿圆柱齿轮三种齿厚参数的微量关系及应用

锁刘佳,王立鼎

(大连理工大学 机械工程学院,辽宁 大连116024)

0 引言

齿轮传动中齿侧间隙的控制,依赖于齿轮零件图上给定合理的齿轮齿厚上下偏差[1-4]。而在齿轮元件设计、齿轮加工与齿轮测量中,经常会遇到齿轮的固定弦齿厚、公法线长度与M值(跨棒距的测量值)之间的尺寸及其公差的换算问题。在一些齿轮手册和资料中,通常会介绍齿轮某两个齿厚测量参数之间增量(与齿厚公差相关)关系的计算式[5-7],但是对三者微量关系的阐述不够集中、完整,有时在同一齿轮公差标准中会出现固定弦齿厚公差、公法线长度公差与跨棒距测量值三种齿厚参数不协调的问题。

针对上述问题,本文阐述了标准直齿圆柱齿轮中固定弦齿厚、公法线长度与跨棒距三种齿厚参数的增量关系,推导出了三者互相变换的简便计算公式,给出了三个常见压力角条件下三种齿厚参数的微量关系图,并对微量关系图的具体应用进行举例,有效提升三种齿厚参数的计算便利性。

1 三种测量齿厚方法

1.1 固定弦齿厚的测量

当标准齿条的齿形和直齿圆柱齿轮的齿形在对称位置上接触时(如图1所示),两接触点之间的距离为固定弦齿厚Sx,而此弦到齿轮齿顶的距离为固定弦齿高hx,它们的计算公式分别为

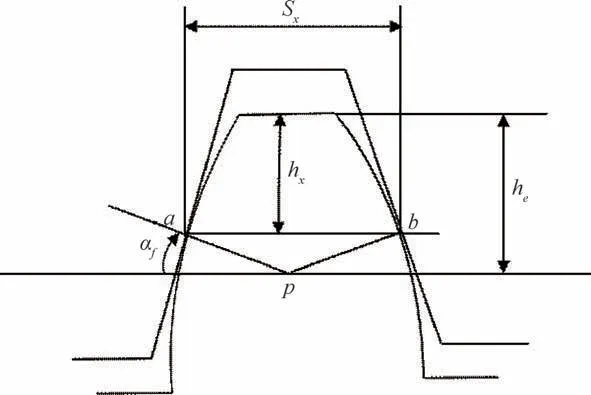
图1 固定弦齿厚Fig.1 Constant chord height

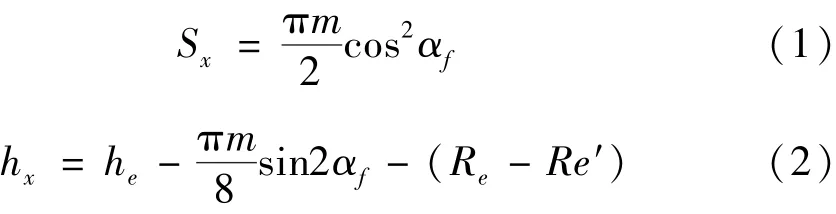
式中:αf为齿轮在分度圆上的压力角;m为齿轮的模数;Re为理论齿顶圆半径;Re′为实测齿顶圆半径;he为齿顶高。

各种标准压力角直齿圆柱齿轮的Sx,hx简化公式如表1所示。

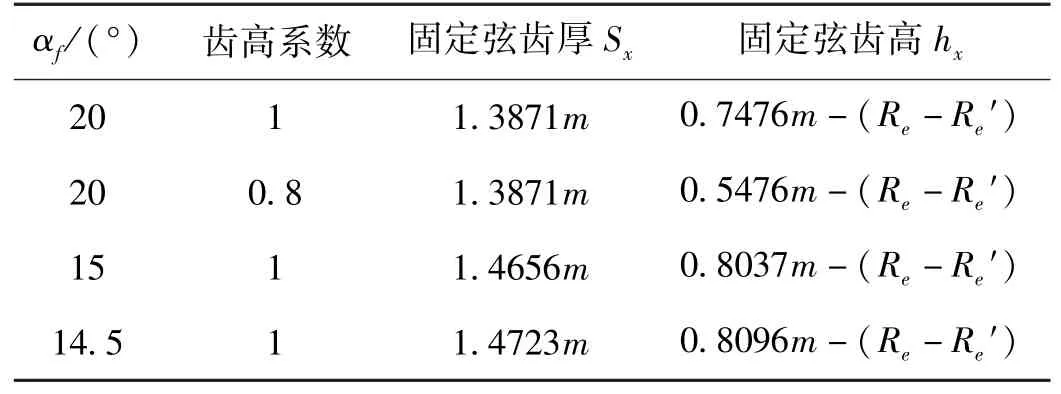
表1 不变位直齿圆柱齿轮Sx,hx的简化计算公式Table.1 Simplified calculation formula of Sx and hx of invariant spur gear

由式(1)和表1可以看出,利用固定弦测量齿厚时不受齿轮的齿数影响,且此方法的计算比较简单。基于该方法的常用量具有:齿轮卡尺、齿厚测量仪、齿厚样板等。但是使用该方法时,齿轮的切向误差、径向误差以及齿顶圆对基准孔的径跳均会对齿厚测量的准确性产生影响[8],故该方法不适用于精密齿轮的齿厚测量,而是多用于ISO 1328-1:2013标准[9]中模数大于1的7级或7级精度以下的齿轮测量。

1.2 公法线长度的测量

图2 齿轮公法线长度Fig.2 Base tangent length

在A和B两点垂直于公法线AB的两直线,即为两齿形的切线,这两条切线互相平行,因此可以利用公法线千分尺的两个平行卡脚测量直齿圆柱齿轮公法线AB的长度Wk,计算公式为

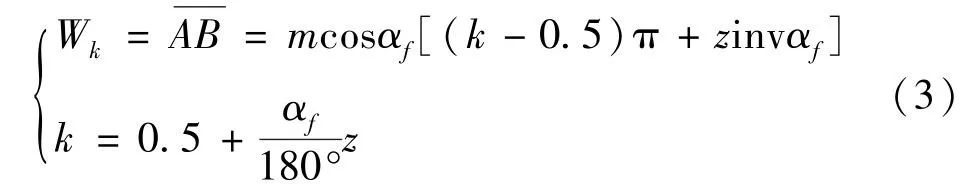
式中:z为齿轮的齿数;k为跨测齿数。

由式(3)可以看出,利用公法线长度测量齿厚的方法的计算过程比利用固定弦测量齿厚的计算过程复杂,但由于采用该方法得到的测量值不受齿顶圆精度的影响,且公法线千分尺的示值分辨力为0.05 mm,因此,该方法可以广泛应用于模数大于等于0.5的7级或7级精度以上齿轮的齿厚测量。

1.3 跨棒距的测量

跨棒距是一种间接测量齿厚的方法[10],其原理如图3所示。理论上,为了使M值确切地反映直齿圆柱齿轮齿厚的尺寸,量棒切线与齿面的接触点应在齿间的固定弦上,此时恰当的量棒直径应为当αf=20°时,dp=1.476m。

图3 奇、偶齿数跨棒距测量Fig.3 Odd and even number of teeth across the rod pitch

由于选取dp=1.476m,而M值通常小于齿顶圆尺寸,导致在模数较小的条件下难以实现M值的测量。目前,在工程应用中通常采用的量棒为测量螺纹的三针量线,测齿轮M值时,其量棒按dp=(1.68~1.9)m选取,接触点在齿轮分度圆附近。不变位的直齿圆柱齿轮M值的计算公式为

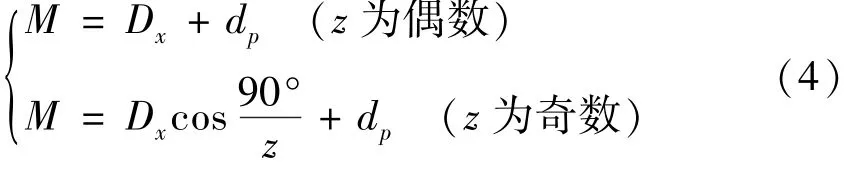
虽然M值的计算比固定弦齿厚和公法线长度的计算更为复杂,但是这种测量方法具有以下优点[11]:

1)适用于中小模数齿轮的齿厚测量,特别是当齿轮模数m＜1时,M值测量的可行性更佳。

2)测量结果精确、数值稳定。由于不需要测量基面,该方法不受齿轮齿圈径向跳动的影响,更不受齿顶圆误差的影响。

3)反映齿厚偏差的灵敏度高。由于ΔM=ΔSxctgαf,在αf=20°时,ΔM=2.75ΔSx(ΔM为M值的变化量,ΔSx为固定弦齿厚的变化量),因此较测量固定弦齿厚及公法线长度相比,该方法的灵敏度更高。在齿轮的齿侧间隙要求十分严格的条件下,选用该方法更具优势。

2 三种齿厚参数的微量关系

2.1 公法线长度与固定弦齿厚参数的微量关系

如图4所示,当固定弦齿厚Sx出现一增量ΔSx=时,齿面在法线方向的增量为即为公法线长度的增量,即在直角Δabc中,由于ab=于是得到

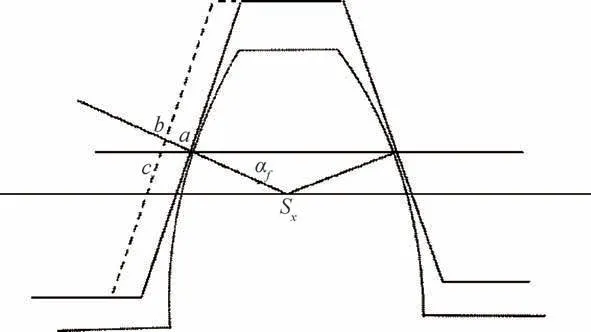
图4 ΔWk与ΔSx的关系Fig.4 Relationship betweenΔWk andΔSx

由于公法线长度测量通常在分度圆附近的齿面上进行,因此式(5)是一个近似计算公式。

2.2 跨棒距测量尺寸与公法线长度的微量关系

对于偶数齿,跨棒距测量尺寸与公法线长度测量之间的相对位置关系如图5(a)所示,M与Wk的微量关系分析如图5(b)所示,当左右齿面各存在时,跨棒与齿面的接触点将由a1移至a2,则可由式(6)得到式(7),即

图5 跨棒距测量尺寸与公法线长度测量之间的相对位置关系以及M与Wk的微量关系Fig.5 Relative position relationship between rod pitch and base tangent length,and relationship between M and Wk

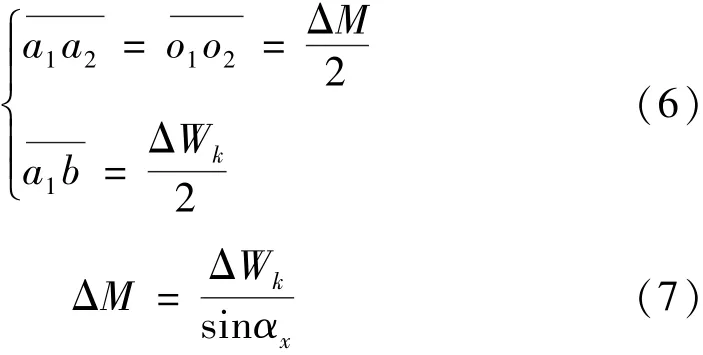
对于奇数齿,其ΔM可表示为

当标准直齿圆柱齿轮、量棒与齿面的接触点在分度圆附近时,有

2.3 跨棒距尺寸与固定弦齿厚的微量关系

将式(5)代入式(7),得到近似计算时,有

2.4 三种测量齿厚参数的微量关系

常用压力角条件下,ΔWk与ΔSx的关系按式(5)计算,二者比值见表2;ΔM与ΔWk的关系按式(7)和式(8)计算,二者比值见表3和表4;ΔM与ΔSx的关系按式(9)计算,二者比值见表5和表6。

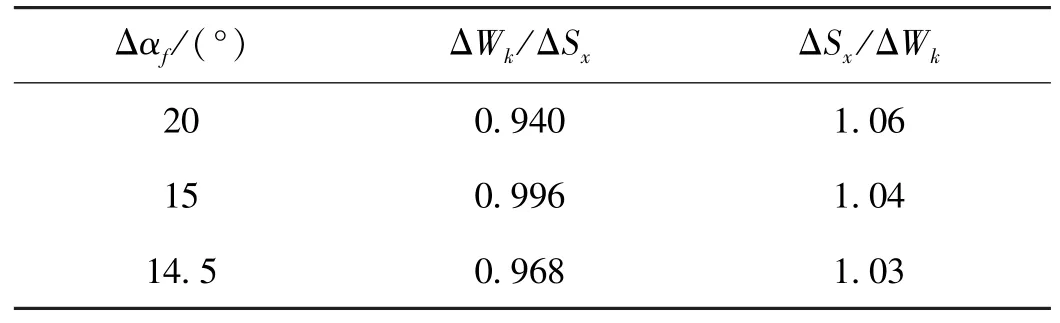
表2 ΔWk与ΔSx的比值Table.2 Ratio ofΔWk toΔSx

表3 偶数齿ΔM与ΔWk的比值Tab.3 Ratio ofΔM toΔWk in even-numbered teeth

表4 奇数齿ΔM与ΔWk的比值Table.4 Ratio ofΔM toΔWk in odd-numbered teeth

表5 偶数齿ΔM与ΔSx的比值Table.5 Ratio ofΔM toΔSx in even-numbered teeth

表6 奇数齿ΔM与ΔSx的比值Table.6 Ratio ofΔM toΔSx in odd-numbered teeth

图6 αf=20°时三种齿厚参数的微量关系Fig.6 Relationship of three tooth thickness parameters at αf=20°

图7 αf=15°时三种齿厚参数的微量关系Fig.7 Relationship of three tooth thickness parameters at αf=15°

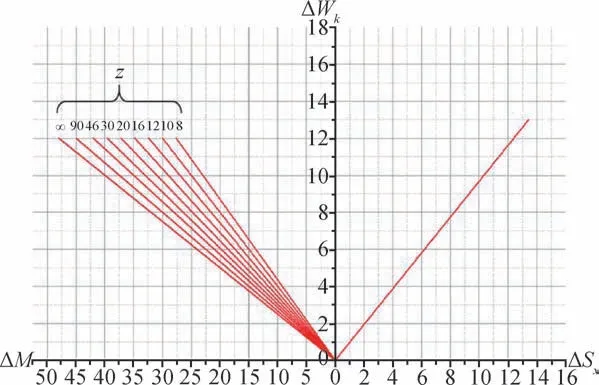
图8 αf=14.5°时三种齿厚参数的微量关系Fig.8 Relationship of three tooth thickness parameters at αf=14.5°

3 三种齿厚参数微量关系的应用举例

3.1 用于公差换算

已知一个不变位的直齿圆柱齿轮,αf=20°,z=30,固定弦齿厚上偏差为-0.020 mm,下偏差为-0.065 mm,求其公法线长度或跨棒距尺寸的上偏差和下偏差。

3.2 用于齿轮加工中的余量换算

一个正在磨削的齿轮,其参数为αf=14.5°,z=25,中途停止磨削进行M值测量,发现按图纸上的最终尺寸尚有ΔM=31 μm的余量,试计算砂轮在齿轮齿厚方向上的余量。

由ΔM=31 μm,可按图8查得ΔWk=9.7 μm。

4 结论

通过对固定弦齿厚、公法线长度与跨棒距三种齿厚参数转换关系进行推导,得到了奇、偶齿的三种微量的转换列式。通过微量转换列式,得出了三种常见压力角条件下三种齿厚参数的微量关系图。本文推导得出的转换列式和微量关系图为工程中三种齿厚参数的计算提供了便利,具有技术借鉴意义。