日韩货物中欧班列海铁联运路径选择研究

吕 靖，张丹阳，季嘉慧

(1. 大连海事大学 交通运输工程学院，辽宁 大连 116026； 2. 大连海事大学 航运经济与管理学院，辽宁 大连 116026)

0 引 言

中欧班列发展日渐完善，已成为亚欧大陆各国政治、经济及文化交流的重要载体。在2020年新冠疫情期间，中欧班列发挥了巨大的战略通道作用。针对中欧班列的发展，国内外学者做了大量研究。王艳波[1]介绍了中欧班列发展现状、发展形势和开行特征，提出了发展规划；JIANG Yonglei等[2]以国内5条中欧班列线路为研究对象，对比分析了海运和铁路运输成本结构差别，结果表明中欧班列相对海运的竞争优势集中在IT产品类。对于多式联运问题，蒋琦玮等[3]考虑碳税值的变化，将运输时间和转运时间设为随机量，构建多式联运机会约束模型，研究了总成本和碳排放量的变化规律，发现充分发挥铁路与水路的优势，对经济和环境都能产生有利的作用；裴骁等[4]考虑组成列车等待时间的要素，以混合时间窗为约束，建立了具有效用值偏好信息的综合满意度模型，对连云港至马德里班列进行了实例分析，得到了不同运输需求下的运输方案；刘清等[5]集成运输成本、运输时间、运输风险和碳排放量等4个因素，构建了基于多目标的长江干线集装箱多式联运路径优化模型，为运输组织者提出了满足差异化需求的运输方案；LIU Zhiyuan等[6]首先将内陆OD需求转化为港口对港口OD需求，然后提出了多式联运结合班轮运输网络设计框架；Y. J. SEO等[7]从时间、成本、风险、距离角度，分析了重庆出口鹿特丹笔记本电脑的7条运输路线；ZHANG M等[8]建立了双层规划模型，分析了碳定价策略、多式联运网络终端布局优化和服务网络优化设计等多种策略组合对发展多式联运的促进作用。

日韩至欧洲的货物运输采用传统海运通道大约需要35天，沿途挂靠港口较多，总线路较长，连通可靠性较低，不能满足货物的运输要求。连通可靠性即网络中路径不中断的概率，如果路径发生中断，不仅会增加运输时间和运输费用，而且会产生巨大的间接费用，影响整个运输方案的可靠性。不中断的概率越高，运输方案可靠性越高。李青林等[9]基于BWM对中欧班列客户需求偏好进行了调查研究，发现运输可靠性是最适合中欧班列发展自身特色的方向；WEN Xin等[10]将基础设施可靠性作为因素加入评估中欧经济通道效用函数中，提出了7种情景，以评估交通运输基础设施可靠性对于路线决策的影响。

上述研究均没有考虑中欧班列作为国际转运通道的可能性，针对中欧班列可靠性研究的相关文献也较少。笔者将中欧班列作为日韩至欧洲国际海铁联运的陆上通道，针对包含中欧班列直达线及中转线的整个运输网络，找寻最优运输路径。首先，根据货主差异化需求，从货主角度出发，以完成一趟货物运送的总费用最小和总可靠性最高为双目标，制定中欧班列海铁联运网络运输方案，分析整体中欧班列海铁联运网络的可靠性；其次，从费用、时间和可靠性等方面，将日韩至欧洲中欧班列海铁联运及传统海运进行对比分析，得出中欧班列海铁联运较优的结论。

1 模型建立

1.1 问题描述

中欧班列运行线分为中欧班列直达线和中欧班列中转线，即从港口直行的中欧班列和内陆铁路枢纽节点城市开行的中欧班列。集装箱货物可由日韩地区集装箱始发港口经海运直接运输，也可经海运至中国的集装箱港站再经由中欧班列直达线或中转线运至欧洲地区目的地城市，如图1。

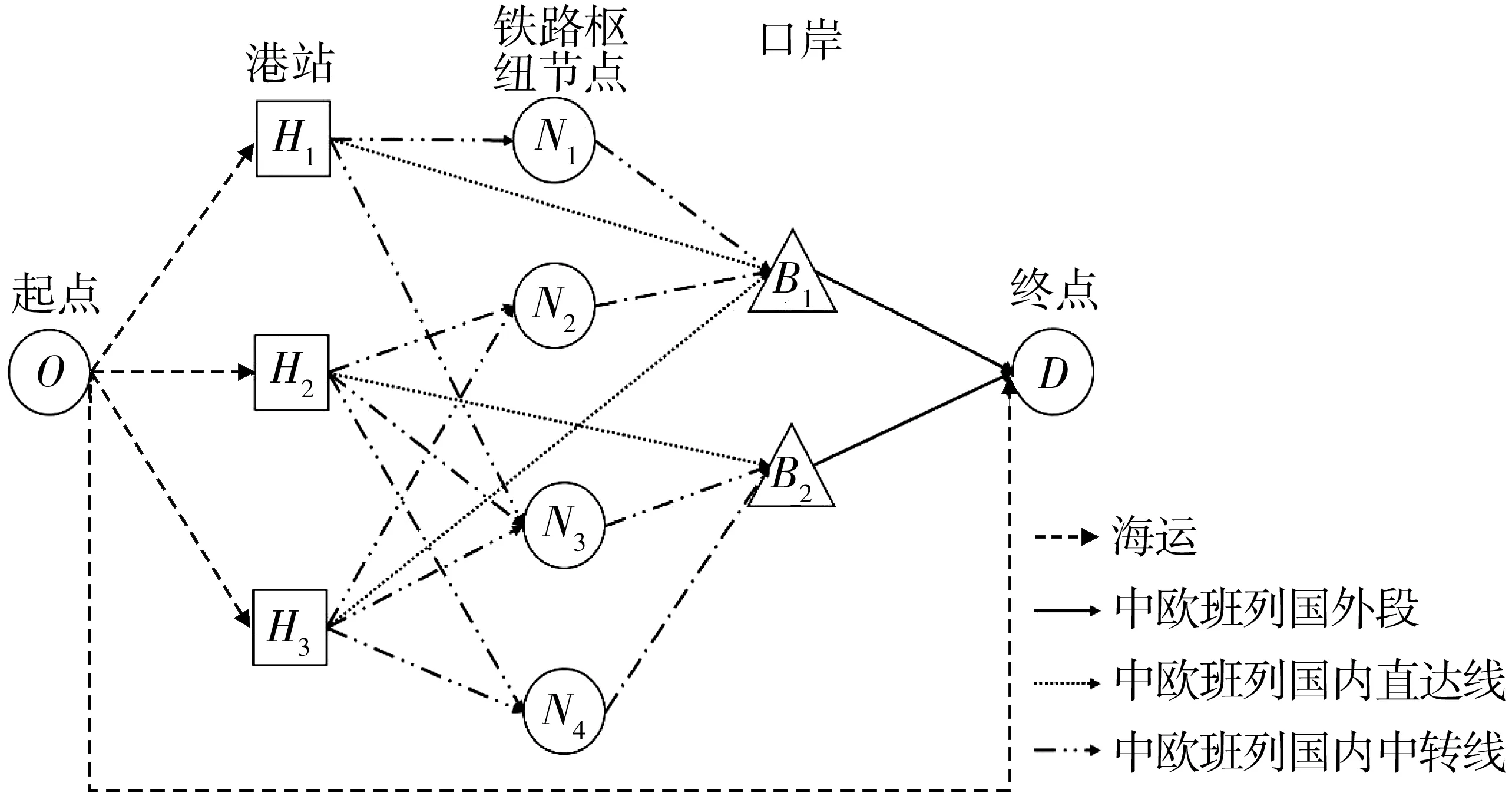
图1 中欧班列海铁联运网络Fig. 1 China Railway Express sea-rail intermodal transport network

在整个运输过程中产生的费用包括：①在海运阶段，付给船公司的运输费用、港站处的中转换装费用；②在铁路阶段，付给中欧班列运营商的运输费用、铁路枢纽站以及口岸站的中转换装费用、等待存储费用、货物时间价值损失产生的费用。所有费用由货主承担。基于此构建模型，选择不同货物的运输路线，目标是使货主花费的总费用最小、总可靠性最高。

1.2 模型假设

1)只考虑40英尺集装箱。

2)研究对象为集装箱重箱流，货运量在运输过程中不发生改变。

3)集装箱货物的单位运输成本与单位运输距离呈正相关关系。

4)集装箱货物的中转换装只发生在节点处，在某一节点处的中转换装不会超过1次。

5)不考虑不同运到期限货物的拼箱运输。

1.3 模型建立

1.3.1 参数定义

N：网络中所有节点集合；

A：网络中所有联弧集合；

M：运输方式集合；

i，j：节点集合中的节点，i,j∈N；

(i，j)：联弧集合中的联弧，(i,j)∈A；

k，l：运输方式集合中的运输方式，k,l∈M；

Q：运输的集装箱数量，箱。

1.3.2 费用模型

1)结合阻抗函数的运输时间T

由于中欧班列货运量的快速增长，某些节点的作业能力会对运输过程产生限制，发生拥堵。因此，在节点发生中转或者换装作业时考虑节点阻抗，即节点时间与节点交通负荷之间的关系，缓解节点拥堵问题。根据阻抗函数定义，结合中欧班列海铁联运网络实际情况，给出结合阻抗函数的运输时间T：

(1)

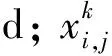
2)运输成本C1

(2)

3)中转换装成本C2

(3)

4)等待存储成本C3

(4)

式中：cw为单位等待存储费用，元/(箱·d)；其他符号同前。

5)时间价值损失VT1

日韩货物大部分为时效优先型货物，运输时间达到一定程度后会随着运输时间的增加而贬值，即时间价值损失费用VT1：

(5)

式中：η为入箱率，%；Pmax为货物满载价值，元/箱；a为货物月贬值率，%；其他符号同前。

6)时间惩罚成本VT2

当货物不能在限期内送达时所产生的时间价值损失即时间惩罚成本VT2：

VT2=cPPmax(T-TP)

(6)

式中：cP为单位送达延误惩罚费，元/(箱·d)；TP为货物的运到期限，d；其他符号同前。

7)货物的时间价值损失VT

(7)

8)单箱总费用F

(8)

1.3.3 路径可靠性模型

路径的连通可靠性为路径节点间不中断的概率，节点间的状态fij为：

由于可靠性包含政治可靠性、运输方式可靠性和基础设施可靠性这3个方面，因此，单个联弧(i，j)上的路径连通可靠性rij按式(9)计算：

(9)

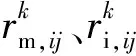
联弧(i，j)间不中断概率为P{fij=1}=ri,j，中断概率为P′{fij=1}=1-ri,j，那么联弧(i，j)不中断概率的期望E[fij]为

E[fij]=1 ×P{fij=1} + 0 ×P′{fij=0}=rij

(10)

因此，联弧(i，j)不中断的概率即期望，所以一条路径的连通可靠性Re为

(11)

1.3.4 目标函数

总费用最小和总可靠性最高的目标函数表达式分别如式(12)、式(13)：

Z1=minF

(12)

Z2=maxRe

(13)

约束：

(14)

(15)

Q≤bi

(16)

(17)

(18)

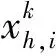
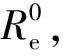
2 求解过程

2.1 目标函数分析

首先对运输成本和运输可靠性这2个目标参数Y按式(19)进行规范化处理，然后将规范化后的目标函数Y*进行加权求和，转化为单目标函数求解：

(19)

在选择路径时，遵循成本最小、可靠性最高原则，同时保持两者之间相互独立。则，转化后的最优目标函数如式(20)：

(20)

式中：ω1、ω2分别为费用、可靠性的权重，ω1∈[0，1]，ω1+ω2=1。

决策者可根据不同货物运输需求决定每个目标函数的权重值。

2.2 遗传算法求解

2.2.1 编 码

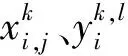
2.2.2 适应度函数构建

在初始种群中，用适应度函数值来评价每个个体是否为可采用的可行解。适应度函数如式(21)：

(21)

2.2.3 选 择

采用轮盘赌法来分配个体选择的概率，被选中的个体作为父代，将更优秀的信息遗传给子代。轮盘赌法的概率公式如式(22)：

(22)

2.2.4 交 叉

2个父代根据交叉概率按照单点交叉方式交换部分基因，产生新的子代。

2.2.5 变 异

在选中的个体上按变异概率随机改变部分基因信息，从而得到新的子代。变异仅在经过的节点进行，首尾点不进行变异。

2.2.6 终 止

以达到最大迭代次数为终止条件。

3 算例分析

3.1 算例描述

假设有2批集装箱，各40个，分别装载笔记本电脑和快消服装，需要从韩国釜山港运至德国汉堡。根据《中欧班列建设发展规划(2016—2020年)》[11]，结合中欧班列各个运输枢纽的发展情况，选取接收日韩货物较多的5个港口和中欧班列发展最好的3个铁路枢纽站作为联运网络节点，如图2。

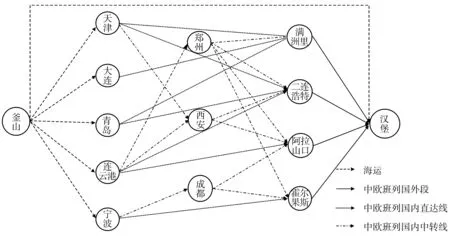
图2 釜山-汉堡海铁联运网络Fig. 2 Busan-Hamburg sea-rail intermodal transport network

3.2 数据收集

1)集装箱海运运价和海运时间由锦程物流网(http:∥www.jctrans.com/)查询可得。

2)中欧班列的国内段运输费用可在中国铁路95306网站(http:∥www.95306.cn/)查询得到；独联体国家、蒙古、欧盟的联合运费分别为3.556、3.696、2.952元/(箱·km)[14]。

3)各联弧的运输时间由节点间的运输距离和运行速度计算得到，班列运输的平均速度为55 km/h。班列平均开行间隔时间Tw=1 d，每天每箱存储费用cw= 300元/(箱·d)。

海铁联运网络运输信息见表1、表2。

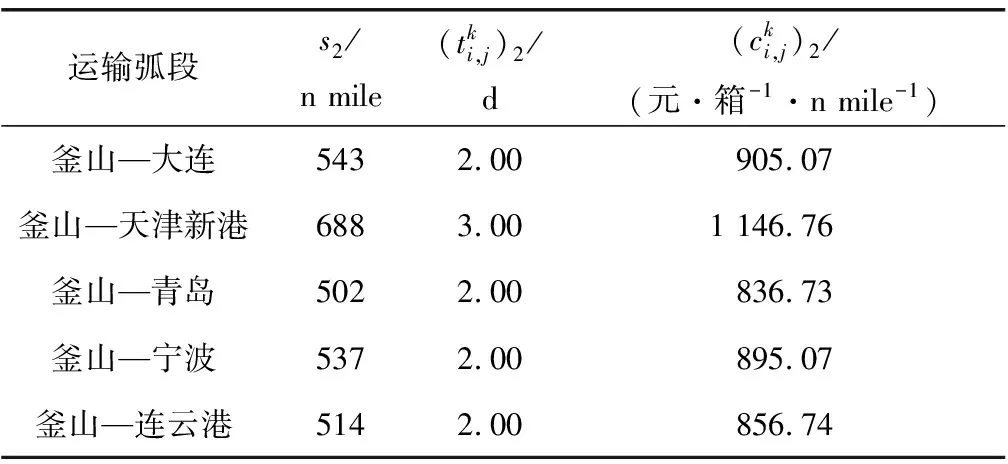
表1 海运弧段运输信息Table 1 Transportation information of marine arc

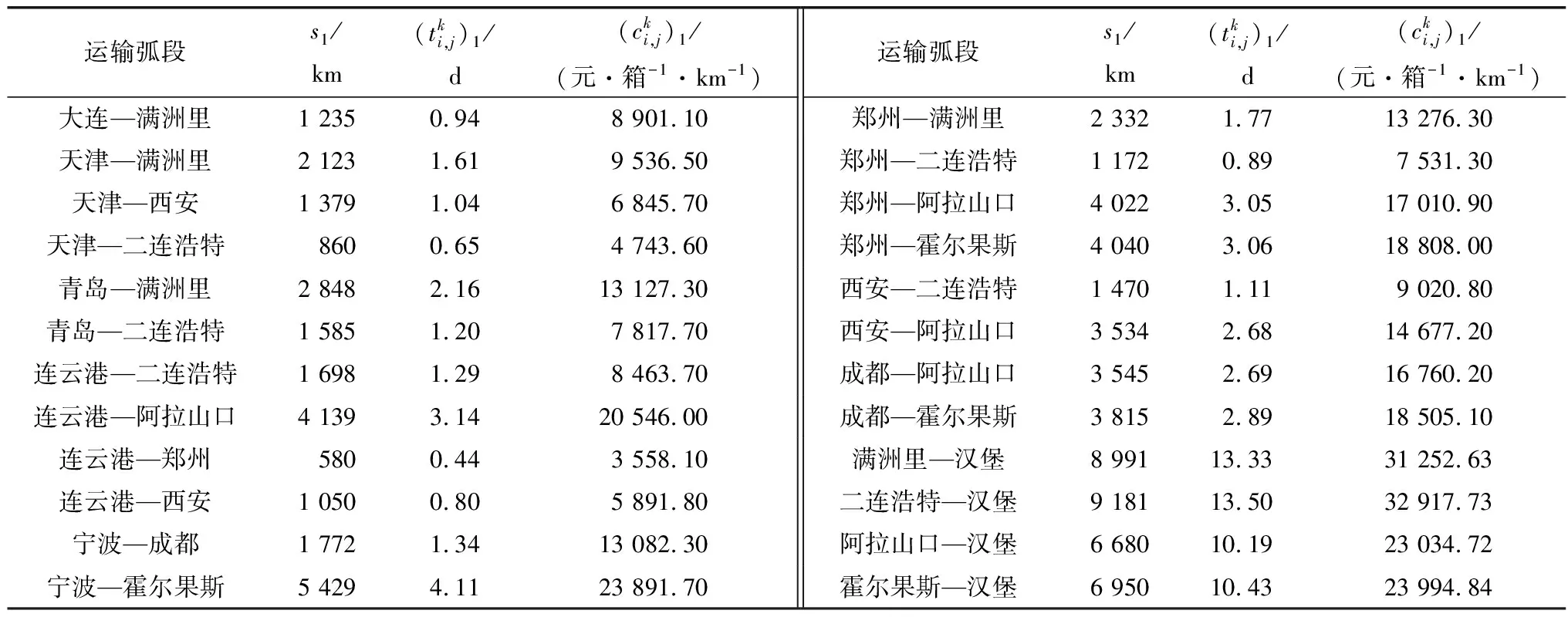
表2 铁路弧段运输信息Table 2 Transportation information of railway arc

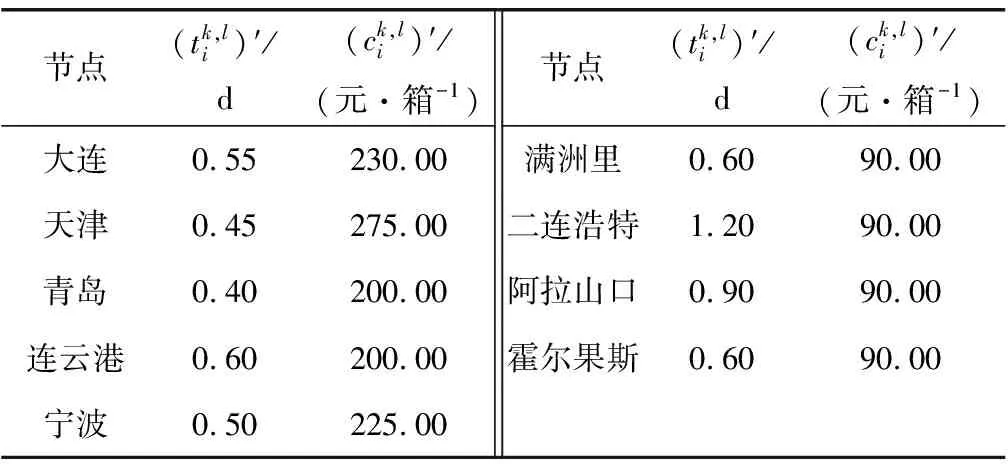
表3 每个集装箱中转节点作业信息Table 3 Operation information of each container transfer node

6)政治可靠性及基础设施可靠性由中欧班列沿线国家环境设定。

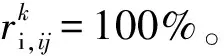
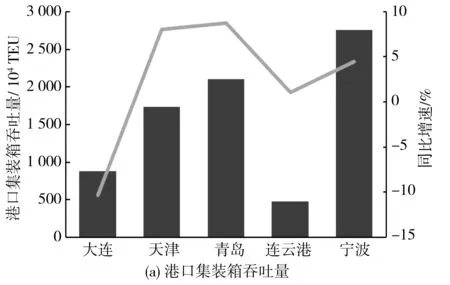
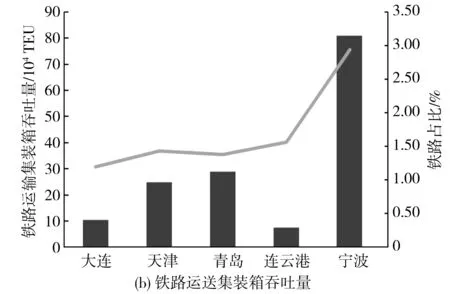
图3 2019年港口及铁路运输集装箱吞吐量Fig. 3 Container throughput of ports and railways in 2019

2019年，各口岸中欧班列通过比例为：阿拉山口33%、霍尔果斯29%、满洲里24%、二连浩特14%[15]。

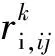
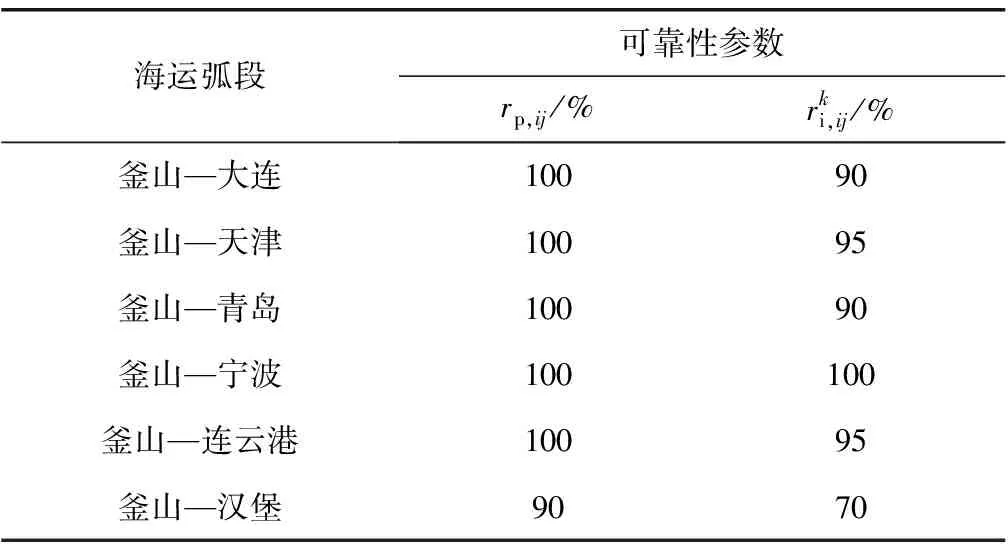
表4 海运弧段可靠性参数Table 4 Reliability parameter of marine arc

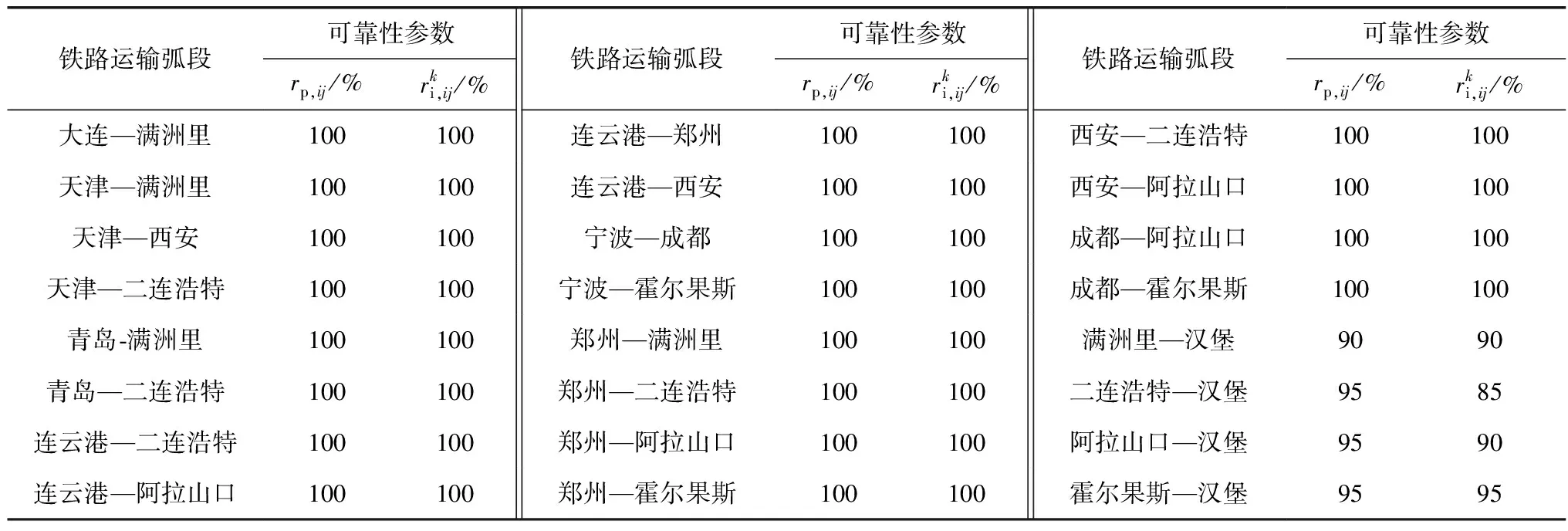
表5 铁路运输弧段可靠性参数Table 5 Reliability parameter of railway arc

4 结果分析

4.1 最优海铁联运方案

运用MATLAB 2016求解，最大迭代次数为100，交叉概率为0.8，变异概率为0.01，在Tp=25 d的情况下，2批集装箱中欧班列海铁联运最优路径选择情况如表6。

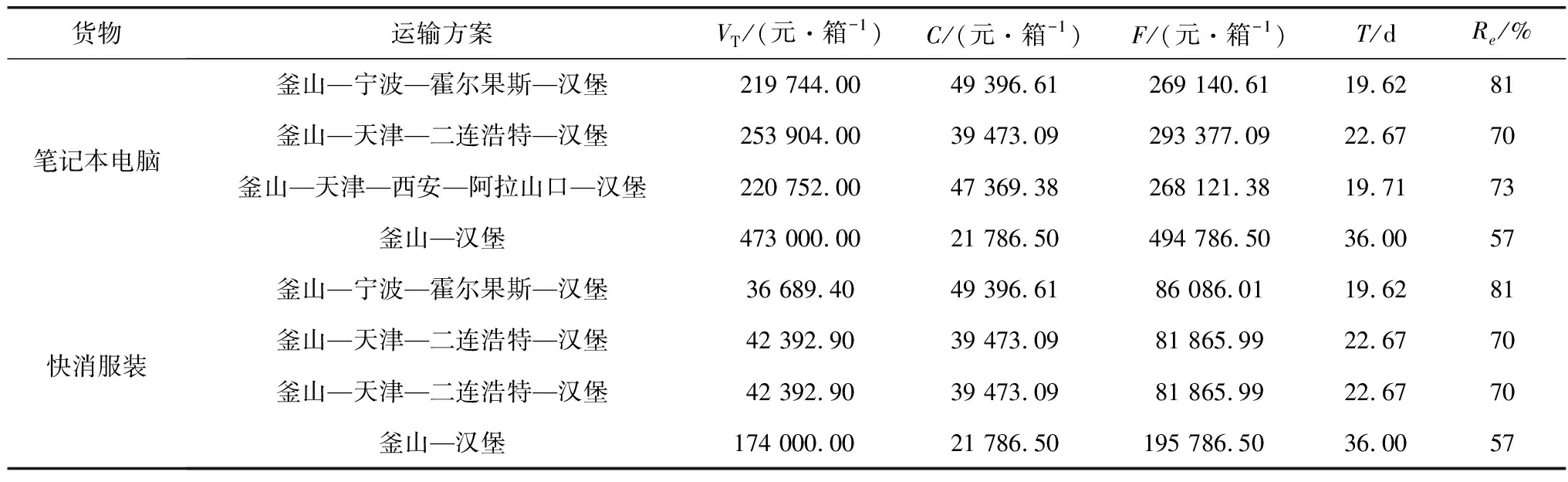
表6 笔记本电脑及快消服装最优海铁联运方案Table 6 Optimal sea-rail intermodal transport plan of laptop and FMCG

由表6可见：

1)优先考虑可靠性时，2批货物均选择釜山—宁波—霍尔果斯—汉堡运输路径，该路径基础设施可靠性最高，海铁联运情况最优，同时，路径运输时间最短，这是由于可靠性较高的路径，不发生中断的概率高，路径运输和节点中转时间都会相应降低，货物运输通畅。

2)优先考虑运输费用时，2批货物均选择釜山—天津—二连浩特—汉堡运输路径，即距离最短的路径。但是，该路径中，二连浩特口岸基础设施不够完善，经常发生拥堵情况，导致整体运输时间增加，时间价值损失费用较高；同时拥堵也会导致运输过程中断，可靠性较低。

3)优先考虑总费用时，综合时间损失费用和运输费用后，笔记本电脑货物选择釜山—天津—西安—阿拉山口—汉堡运输路径，快消服装货物则仍然选择釜山—天津—二连浩特—汉堡运输路径。原因是快消服装的满载价值和货物贬值率都低于笔记本电脑，其时间损失费用对总费用的影响较小。

4)将最优运输方案与现有海运路线相比，发现中欧班列海铁联运路线时间比现有海运路线均少1/2，可靠性优于现有海运路线，而运输费用高于现有海运路线，但是，由于时间价值费用可以抵消运输成本增加带来的影响，因此总费用皆低于现有海运路线。不过，我国各级政府为中欧班列的运行提供了一定的补贴，从而可以缩小中欧班列海铁联运与现有海运的运输费用差距。

4.2 海铁联运网络可靠性分析

笔者选择日韩至欧洲笔记本电脑海铁联运网络进行可靠性分析。

1)如果运输过程不发生中断，即各路径可靠性都为1，则最优运输方案为釜山—天津—西安—阿拉山口—汉堡。

2)如果考虑某个节点中断对整体海铁联运网络的影响，网络中除起始点外共12个节点，每次删除1个节点，运行结果显示共有3个节点在删除之后最优海铁联运方案发生了变化，变化后相对于网络整体不中断时的最优运输方案增加的时间和成本如表7。

表7 可靠性分析结果Table 7 Reliability analysis results

由表7可知，当中欧班列海铁联运网络中的某些节点发生中断后，最优运输方案会发生变化，但是运输时间和总费用的变化幅度非常小。说明中欧班列海铁联运网络的整体可靠性较强，某个节点的中断不会对中欧班列海铁联运网络造成太大的影响。

5 结 论

从货主角度出发，以完成一趟货物运输的总费用最小和总可靠性最高为双目标，制定中欧班列海铁联运网络运输方案，分析了整体中欧班列海铁联运网络的可靠性；从费用、时间和可靠性等方面，将日韩至欧洲现有海运及中欧班列海铁联运进行对比分析。得到以下主要结论：

1)中欧班列海铁联运对于运送日韩快速货这类时效优先性货物有很大的发展潜力。

2)中欧班列海铁联运网络的整体可靠性强，不会因某个节点的中断而受到很大影响，优于现有海运。