零担物流线路组合选择策略研究

闫 芳，郭 俊，陈 凯

(重庆交通大学 经济与管理学院，400074 重庆)

0 引 言

随着物流业的不断发展，公路物流货运量保持着强劲的增长势头。在GDP不断增长与社会生产柔性化发展的双重推动下，零担物流得到了越来越广泛的关注。那么在零担物流中，承运人如何在已有运载资源配置的情况下，根据托运任务间的协同效应选择最佳运输任务组合是一个关键问题。

目前，关于运输任务选择的研究主要从整车运输(truck load,TL)承运人的视角出发。从建立模型的角度来看，C.G.LEE等[1]建立了非线性整数规划模型，并采用基于列生成和拉格朗日的启发式算法求解，使承运人得到组合拍卖中的最优任务组合；X.H.QIAN等[2]针对第4方物流供应商通过组合逆向拍卖购买运输服务情况，将防御策略、保留策略和外部期权策略相结合，构建了两阶段随机竞胜标确定模型；Y.FANG等[3]讨论了包含承运人、托运人以及第3方承运人的运输服务采购竞胜标问题，针对传统混合整数线性规划模型求解易陷入分枝树和定界树不平衡的问题，构建了一个确定模型；C.TRIKI等[4]将运输服务采购拍卖和生产调度决策问题相结合，构建竞胜标确定问题模型，并开发了2种启发式算法对模型求解；G.KUYZU等[5]建立了随机投标价格优化模型，以选出承运人满意的任务组合方案；闫芳等[6-7]则考虑承运人与托运人的合作与竞争关系，建立了双层规划模型以解决承运人选包问题。从考虑任务组合的协同效应的角度来看，E.OLCAYTU等[8]提出了一种基于任务之间协同的竞价方法，并模拟实验证明其有效性；F.YAN等[9]考虑了已有任务和新任务间的协同效应，构建了运输服务竞价问题模型，并设计了一种基于粒子群优化的智能算法对模型求解;C.TRIKI等[10]利用基于位置技术的优化方法评估托运任务间的协同作用，使承运人减少空车移动距离从而增加收益。

在零担物流(less than truckload,LTL)中如何快速有效地选择运输任务的研究相对较少。文献[11]从零担物流的角度出发，提出了一种混合整数规划方法以解决运输服务采购投标问题。文献[12]为了解决小规模的零配件运输问题，提出了一种迭代请求交换机制，证明组合包多轮交换机制能有效提高承运人收益。以上研究都是利用智能算法求解承运人选包问题，运算耗时长、求解结果不稳定。笔者基于承运人的视角，建立可搭载零担物流选包和车辆路径优化模型，提出了一种基于托运任务间协同效应的零担物流选包策略，以解决承运人选包和路径优化问题，并选取2个算例对其有效性和可行性进行验证分析。

1 问题描述及建模

1.1 问题描述

假设在可达区域内有V个节点，节点间的距离已知。某承运人已承运任务集为M0，M表示现货市场待选任务集，且托运任务的起止点、物流量和运输费用等信息已知。那么该承运人需要考虑2个问题：①如何在已有任务M0的基础上选择M的任务子集，使其运输决策最优；②如何规划车辆行驶路线，运输完成M的任务子集和M0，以达到收益最大。

1.2 模型假设

模型存在以下假设：

1)假定不同托运人的货物可以混装，但不可拆分；

2)每个托运任务的信息已知；

3)油耗与车辆的负载率成线性相关[13]；

4)车辆折旧系数根据工作量法计算；

5)车辆类别相同，高速收费系数唯一；

1.3 参数定义及数学模型

参数定义如表1：

表1 参数定义Table 1 Parameter definition

决策变量有：

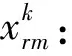
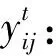
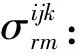
承运人零担物流选包和车辆路径问题模型为：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

目标函数式(1)表示承运人收益最大化；式(2)表示流量平衡；式(3)表示车辆经过边(i,j)时货物装载总量；式(4)表示车辆经过边(i,j)时货物装载率；式(5)表示车辆容量限制；式(6)表示车辆最大行驶距离约束；式(7)表示车辆在边(i,j)上的单位油耗成本；式(8)、式(9)表示接受的任务必须全部完成；式(10)、式(11)表示二进制变量的取值范围。

2 模型求解

在零担物流中，无论是选择任务组合还是规划路径都属于NP-Hard问题[14-15]，求解过程较为复杂。因此，笔者提出了一种基于托运任务间协同效应策略的2阶段算法，并通过其对模型求解。第1阶段采用协同效应策略完成现货市场任务选择；第2阶段规划车辆路径。

2.1 协同效应策略

2.1.1 协同效应影响因子

为衡量现货市场可选任务组合S与承运人已有任务间的协同效应，将协同效应显著的组合作为承运人的最优选择，笔者综合选取了7个能够集中体现2者协同程度的影响因子作为研究对象。

1)任务组合S运输成本与车辆行驶距离

文献[8]提出，承运人为完成任务而付出的单位距离成本是衡量任务间协同程度的重要指标。换言之，单位成本距离越小，任务间的协同效益更高。由此，可将运输成本C(S)与车辆行驶距离d(S)的协同值定义如式(13)：

(13)

2)报价与行驶距离

在报价既定的情况下，更小的运输距离代表任务间拥有更高的协同。承运人单独承运任务组合S时，其报价P(S)与行驶距离d(S)之间的协同值计算如式(14)：

(14)

3)起点节点与行驶路线

r3表述为：车辆行驶距离与任务组合S中各任务的起点节点到只承运M0时运输路线各节点的最短距离之和的比值。笔者在文献[10]的基础上，提出了一种新的求解r3的方法。首先，将任务组合S包含任务数记为nS；其次，利用EOPSO[16]计算承运人只承运M0时，其行驶路线R(M0)和行驶距离d(M0)；最后，计算第i个任务的起点与R(M0)各节点距离的最小值dM0(i)。对数据进行归一化处理后计算如式(15)：

(15)

4)终点节点与行驶路线

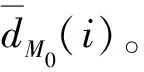
(16)

5)起点节点与各节点的跳跃点数量

待选任务起点与M0运输路线节点间的可达性是体现其协同效应的重要指标。跳跃点数量越少，表明协同程度更高。将任务i的起点到R(M0)各节点的跳跃点最小值记为ZM0(i)，运输网络中任意2节点之间跳跃点个数的最大值记为nmax。协同值r5的计算如式(17)：

(17)

6)终点节点与各节点的跳跃点数量

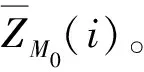
(18)

7)在承运M0时，组合S可搭载的概率

笔者从零担运输的角度来研究线路组合选择，因此还需考虑待选任务与车辆可用载重之间的协同。首先，将任务i的运量q(i)依次插入到R(M0)后的量记为g(R)，R(M0)包含的节点个数记为nR(M0)；然后，将g(R)的元素与车辆最大载重Q比较，若大于Q，则说明任务i在R(M0)的此节点不能搭载，反之，则可搭载；最后，将可搭载的节点个数记为H(i)。协同值r7的计算如式(19)：

(19)

2.1.2 影响因子权重

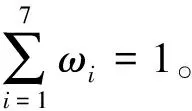
BP神经网络具有自我学习能力、自适应能力、强大的非线性映射能力以及高容错性，适合求解具有多因素的综合评价权重确定问题[18]。笔者选取BP神经网络解决因子权重确定问题。权重ωi的计算步骤如下：

步 骤 1：建立神经网络。将七个因子的值作为BP神经网络的输入层神经元，建立一个3层的BP神经网络。

步 骤 2：确定隐含层。采用文献[19]提出的试凑法确定其个数。

步 骤 3：计算承运人收益。采用EOPSO计算现货市场所有任务组合S与已有任务M0合并后的收益。

步 骤 4：确定输出层。将步骤3计算的结果进行归一化处理，并将结果作为输出层神经元。

步 骤 5：训练。利用BP神经网络工具箱进行训练，从而得到各因子的权重。

2.2 算法设计

2.2.1 任务选择

采用协同效益策略对现货市场任务进行选择。首先，计算承运人已有任务与所有现货市场任务组合的协同值；其次，将最大协同值所对应的组合作为承运人在现货市场上的选择。

2.2.2 车辆路径规划

针对标准粒子群优化算法易陷入局部最优、进化后期收敛速度慢和收敛精度低等缺点,笔者采用精英反向学习的粒子群优化算法对车辆路径规划求解。具体步骤如下：

步 骤 1：初始化，随机生成各粒子位置和速度。vi和pi都是一个N·2R的矩阵，其中R为任务个数，N为粒子个数。

步 骤 2：车辆运输路径规划。

1)将每个任务拆分为pickup任务和delivery任务，并重新编号；

2)根据pi前2R列，进行升序操作，确定任务拆分后的操作先后顺序；

3)标记P-D操作。

(a)按照优先顺序，寻找未拆分时相同任务编号的位置；

(b)将位置较小者标记为该任务的pickup点，较大者标记为delivery点。

4)规划路径。

(a)根据操作优先顺序，确定车辆首个任务；

(b)将当前节点加入到路径集合，并更新车辆剩余运力；

(c)根据顺序确定下一任务；

(d)判断该任务的操作性质，若为pickup点则进入步骤(e)，若为delivery点则进入步骤(f)；

(e)判断车辆剩余运力与任务量的大小关系。若剩余运力小于任务量，则将该任务标记后抛弃，并返回步骤(c)；否则进入步骤(f)；

(f)完成任务相应的装卸操作，更新车辆剩余运力和路径集合；

(g)判断未标记任务是否已经完成。若还存在未完成的任务，则返回步骤(c)。若不存在则进入步骤(h)；

(h)根据原有优先顺序，完成标记任务的路径规划；

(i)采用插入法确定最优的路线拆分位置，满足车辆行驶里程约束；

步 骤 3：求解路线载重、车辆载重率，计算运输成本，记录最优值。

步 骤 4：更新粒子。

1)判断每个粒子的上下界；

2)根据上下界和个体最优生成反向精英粒子，并规定其上下界；

3)判断反向精英粒子与各粒子上下界的大小关系。若反向精英粒子大于上界或者小于下界，则反向精英粒子为上下界之间的随机数。

步 骤 5：利用差分演化策略，更新全局最优解。

步 骤 6：判断是否达到最大迭代次数。若未达到则返回步骤4；反之，则进入步骤7。

步 骤 7：结束。

整体算法流程如图1。

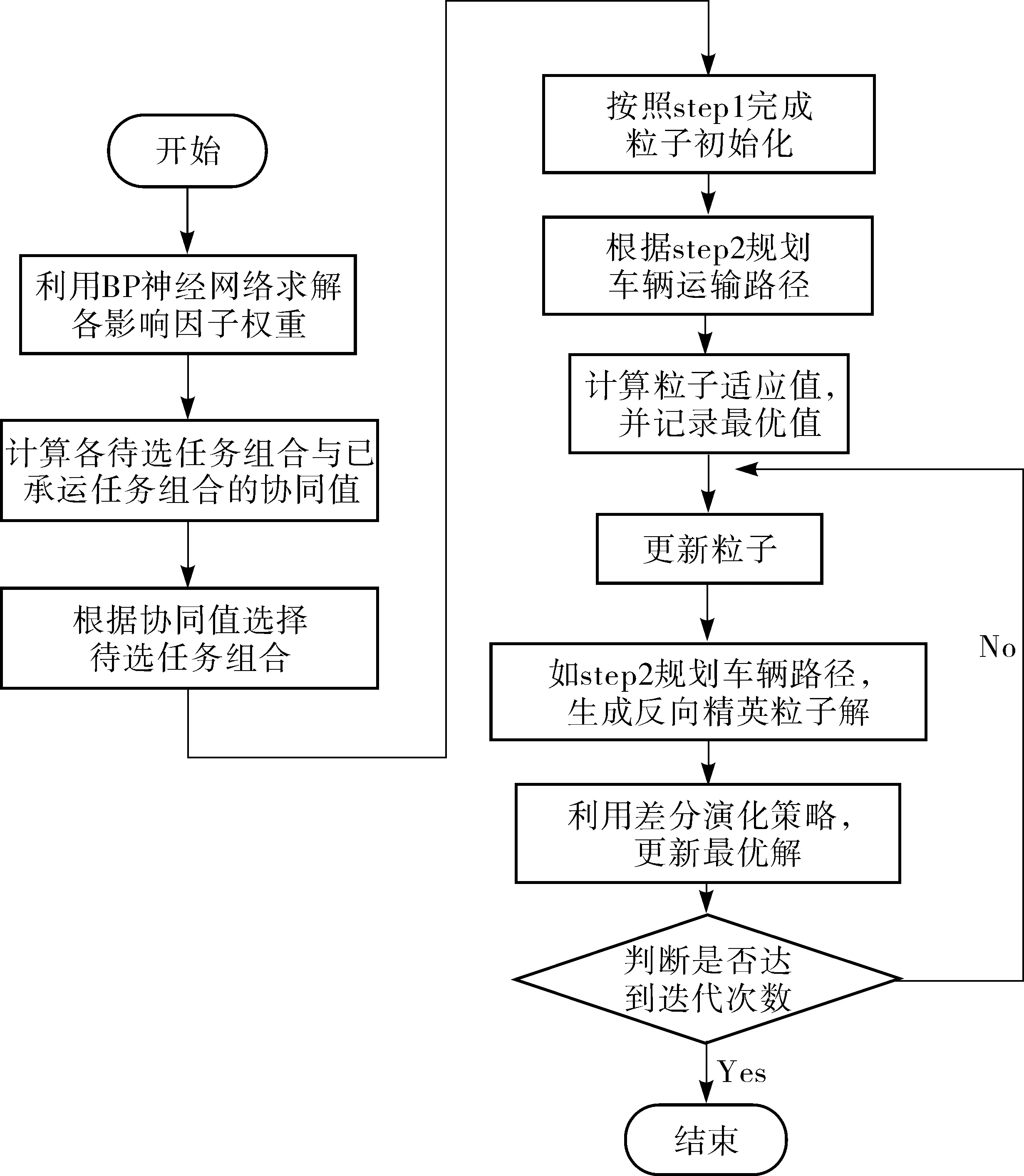
图1 算法流程Fig. 1 Algorithm flowchart

3 算例分析

为验证协同效应策略的有效性和可行性，笔者采用间协同效应策略和EOPSO[15]对两个算例进行分析讨论。

首先，计算现货市场所有任务组合与M0合并后的各因子的协同值；其次，利用EOPSO计算任务合并后承运人的收益(粒子群参数设置为：种群规模为20，迭代次数为200，学习因子c1=1.5，c2=0.3，ωmax=0.4)；最后，将协同值最大的组合包的收益与承运人的最大收益对比，如果二者相近，则证明协同效应策略在解决零担物流承运人选择任务组合时有较好的可行性和有效性。

车型和油耗资料来源于文献[12]，表2和表3中任务节点的距离和跳跃点数量来源于360地图，货物运输费用1.0元/kg。算例1和算例2任务数据都来源于互比物流网站(www.hubiwl.com)。

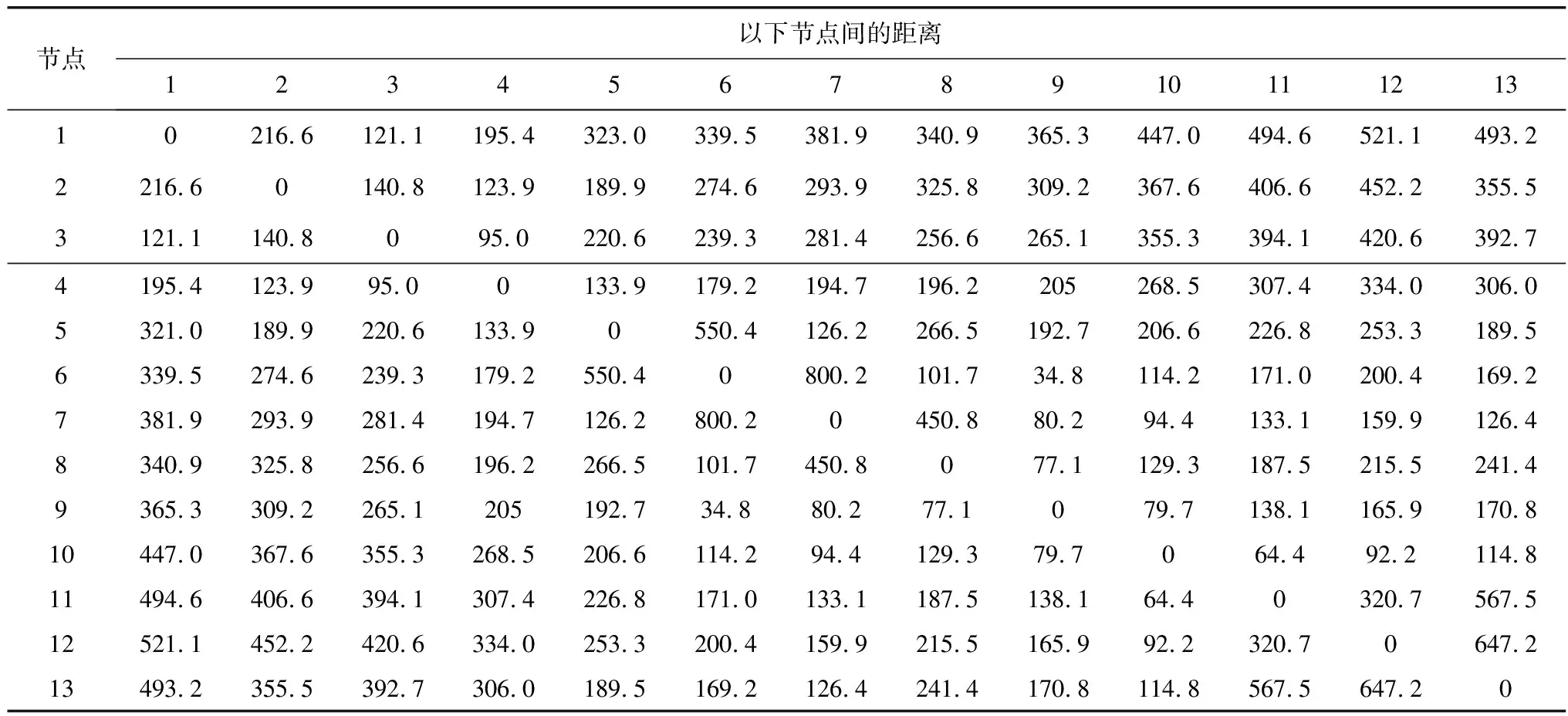
表2 节点间的距离Table 2 Distance between nodes km

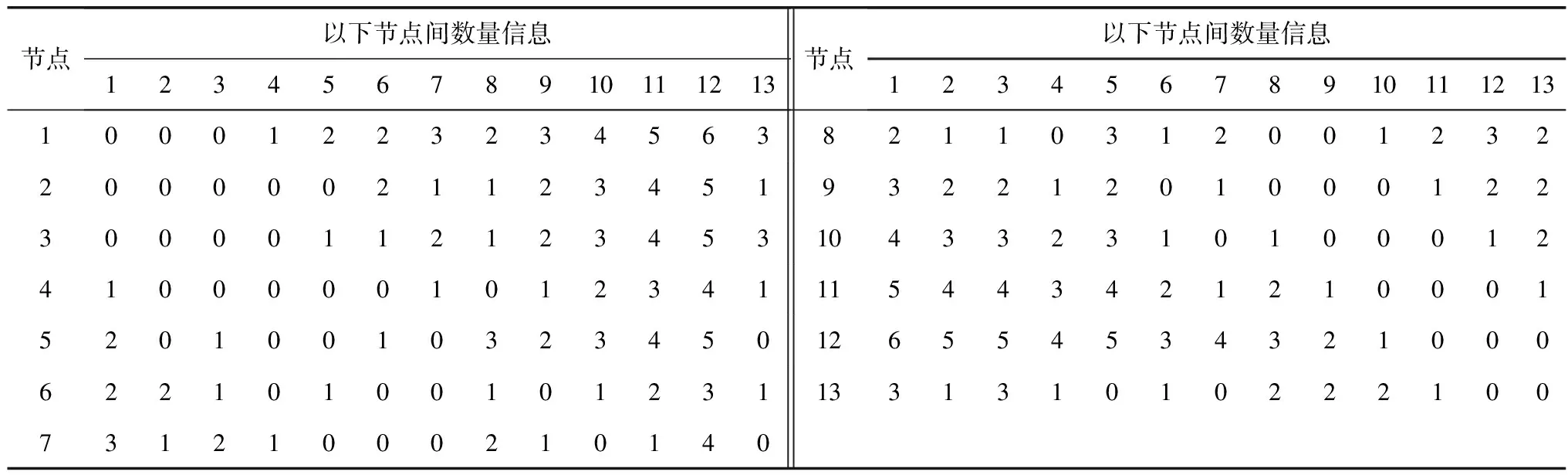
表3 节点间的跳跃点的数量信息Table 3 Number information of jump points between nodes

3.1 算例1

算例1任务信息如表4，现货市场托运任务M有24-1=15种组合，包含的任务如表5。首先，将所有任务组合S的收益归一化处理；然后，将15种任务组合中的70%(11种任务组合)作为训练样本，15%(2种任务组合)作为验证样本，剩下的15%作为检测样本，调用BP神经网络工具箱进行训练，训练结果如图2；最后，根据训练的结果求各因子的权重，其结果为：r1=0.36、r2=r3=0.18、r4=0.02、r5=0.03、r6=0.12和r7=0.13。

表4 算例1任务信息Table 4 Task information of example 1

表5 组合包S所包含的任务Table 5 Tasks included in the package S

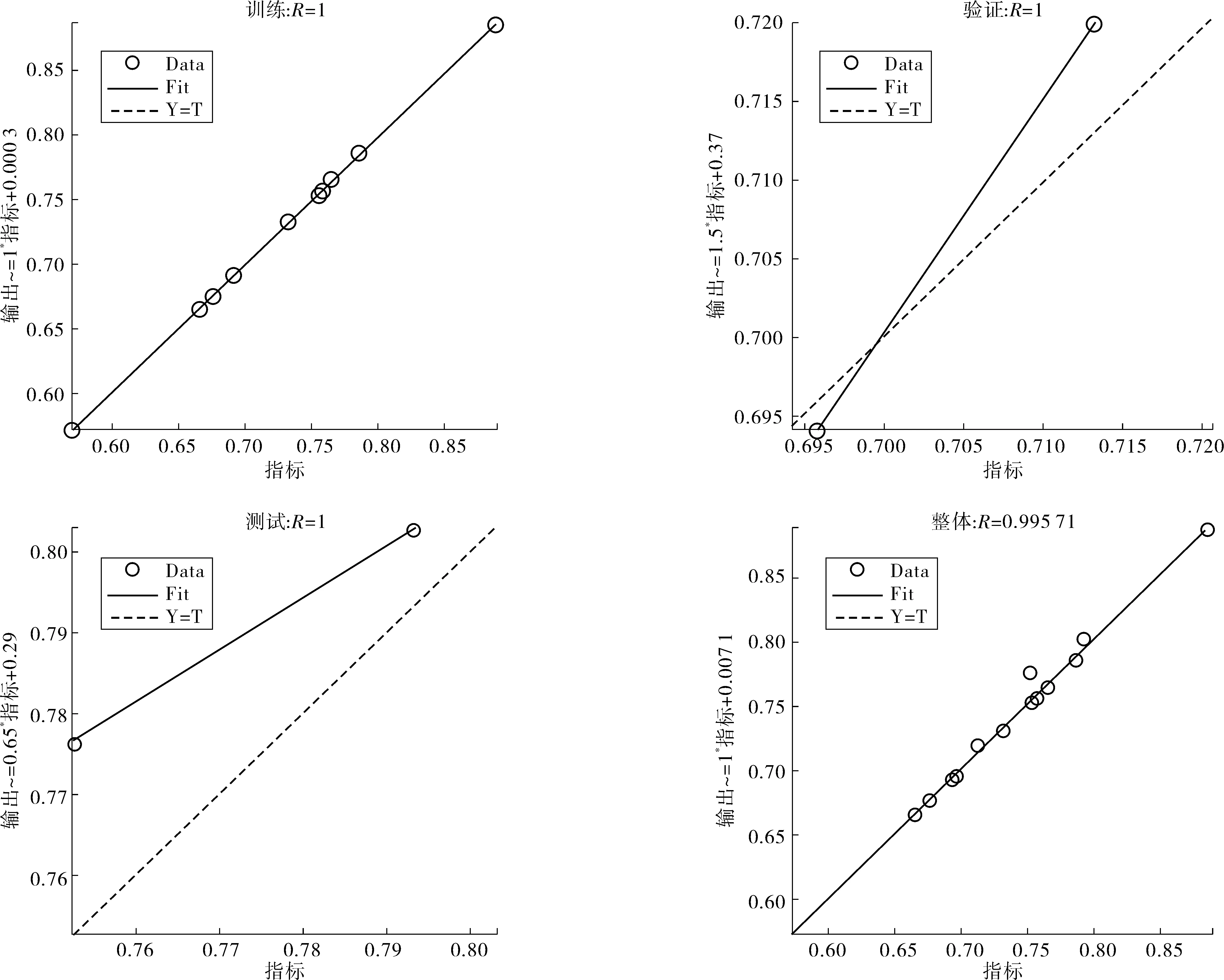
图2 BP神经网络训练结果Fig. 2 BP neural network training results

承运人只选择任务N2时，协同效应值最大为0.89，利用EOPSO计算承运人的收益最大为1 108元，如表6。将承运人已有任务集合M与新增任务N2合并，得到承运人的运输任务集合。在允许搭载的情况下，对其运输线路进行合理规划， 计算结果如表7。其中，第1列表示车辆的运 输路径，如车辆 1的路线为2-5-8-9-6，表示车辆从节点2出发，途径节点 5、8和 9，之后到达节点 6； 第2列表示在该节点相关运输任务的装货操作，第3行表示在该节点相关运输任务的卸货操作。如车辆2的行驶路线为3-1-3，表示车辆在节点3装载任务E2，行驶到节点 1后，卸载E2并装载新任务E1，最后返回到节点3，卸载任务E1。通过分析 发现，任务E4与任务E3存在相同节点。因此，综 合考虑各节点间的距离后，在搭载任务E4的同时，完成任务E3和任务N2能够最大程度上节约成本。因此，在此决策方案下，承运人总体收益最优，为1 108元。

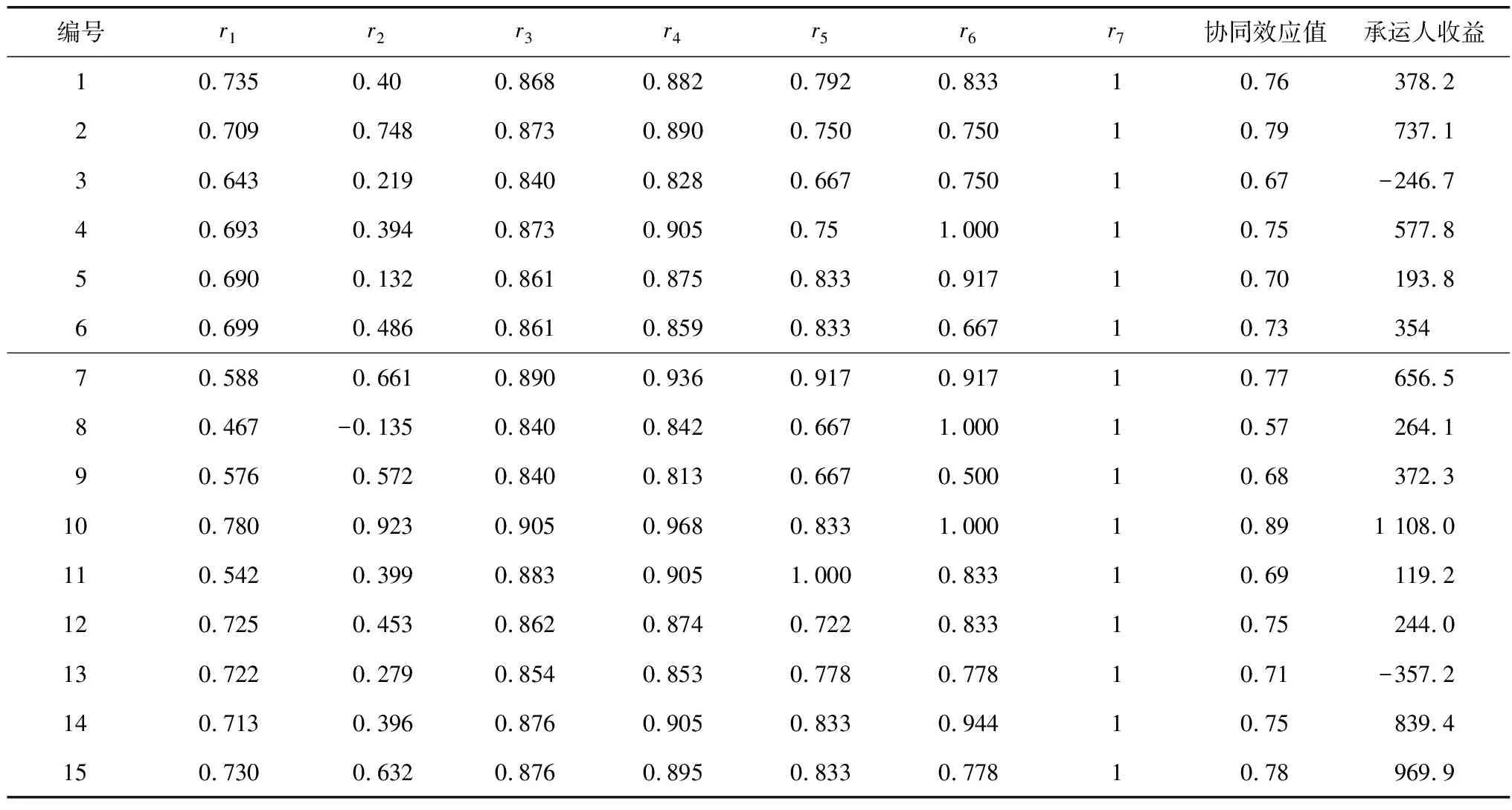
表6 算例1计算结果Table 6 Calculation results of example 1

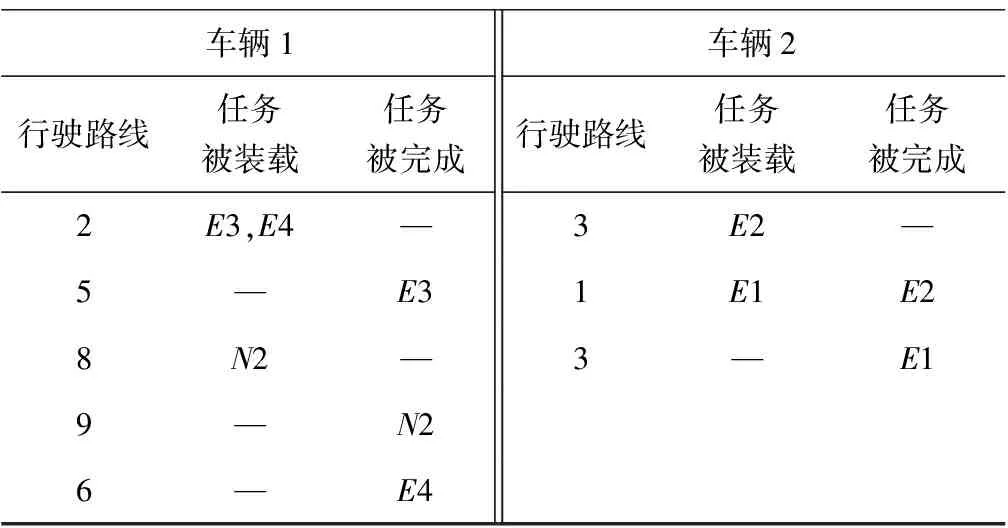
表7 承运人车辆行驶路线信息Table 7 Carrier vehicle driving route information

算例1中分别采用协同效应策略与EOPSO求解，2者最优方案相同，均选择N2作为承运人的新增线路，因此，协同效应策略与EOPSO在计算结果质量方面表现相同，但是在计算时间上，采用协同效应策略选择任务仅需120.6 s，而采用反向精英粒子群算法则需要1 895.7 s，前者节约了近93.64%的运算时间。在时间计算方面，采用协同效应策略选择现货市场任务组合更具有优势。

3.2 算例2

为了进一步验证模型、协同效应策略的适用性，算例2扩大了任务规模，包含31种任务组合，包含的任务如表8。通过计算，承运人在M0的基础上选择承运任务N2、N3和N4时，其协同效应值最大为0.927；利用EOPSO计算在此情况下承运人的收益为943.7元，其收益在所有任务组合里依然最大。因此，基于托运任务间协同效应的求解策略与EOPSO求解质量相同。

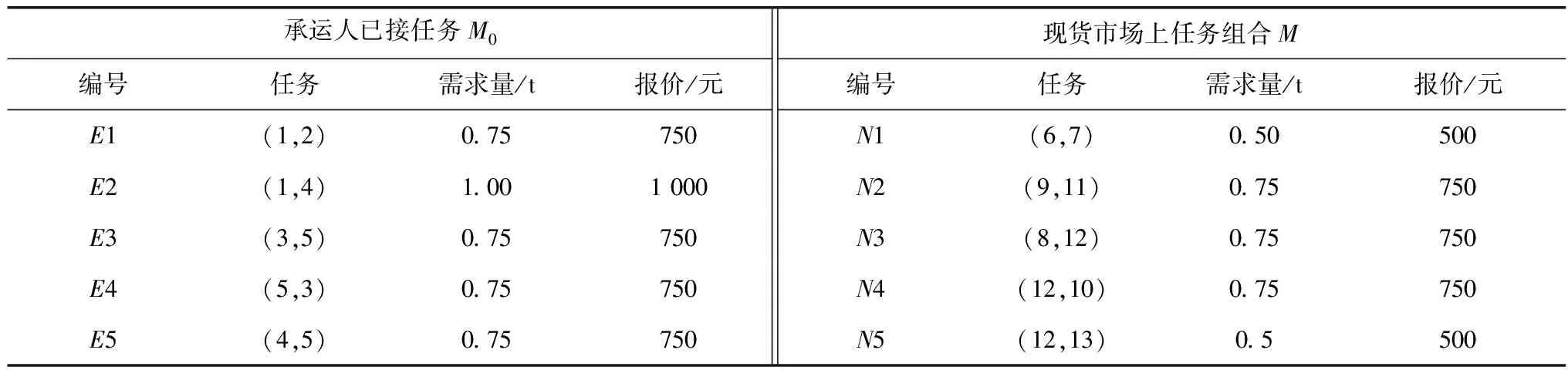
表8 算例2任务信息Table 8 Task information of example 2

选择任务N2、N3和N4作为新任务时，路径规划结果如表9。需要2辆车完成承运的8个任务，行驶路线分别为1-3-4-5-2-3和8-9-12-10-11。对路线分析可知，任务E1和E2在节点1同时被装载，所以将任务E1和E2进行了合并运输。综合考虑各节点间的距离、装载和卸载情况，通过计算可知，在搭载任务E1的同时，完成任务E2、E3和E5能够最大程度上节约运输成本。算例2在考虑承运人收益最大化的前提下，选择N2、N3和N4的任务组合作为新增任务，得出最大收益为943.7元。与算例1结果相似，两者在解的质量方面表现相同。但EOPSO耗时4 125.9 s，协同效应策略仅耗时148.6 s，节约了96.4%的运算时间。

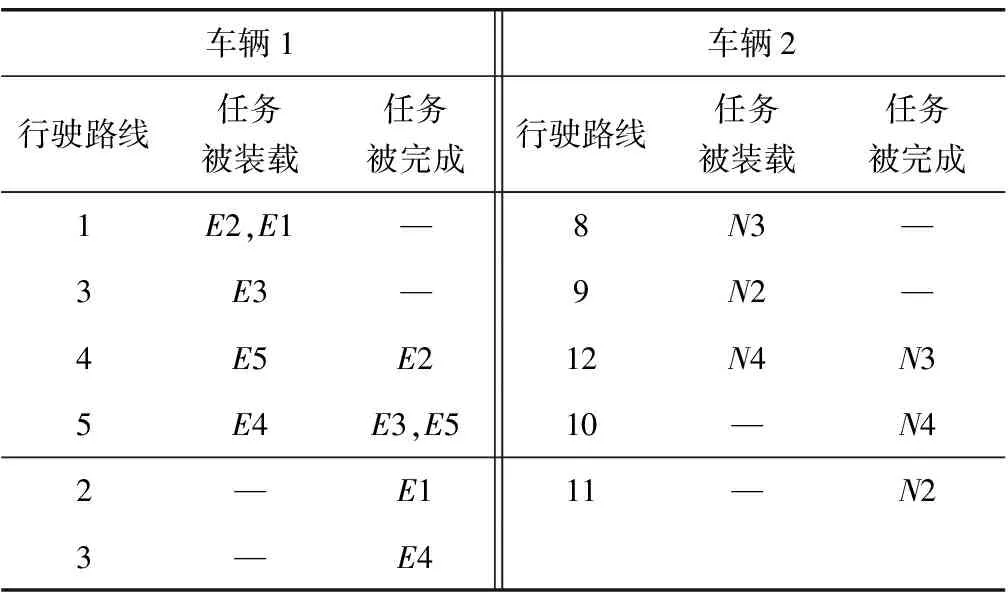
表9 承运人车辆行驶路线信息Table 9 Carrier vehicle driving route information

为说明算例2结果的有效性和合理性，将选择全部任务的收益与协同效应策略得到的最优解进行对比。如表10，后者车辆行驶的总距离比前者减少33.63%，且空载距离减少46.51%。因此当承运人放弃现货市场任务N1和N5时，其车辆行驶总里程和空载距离均不同程度的减少，且收益从-528.3元增加到943.7元。

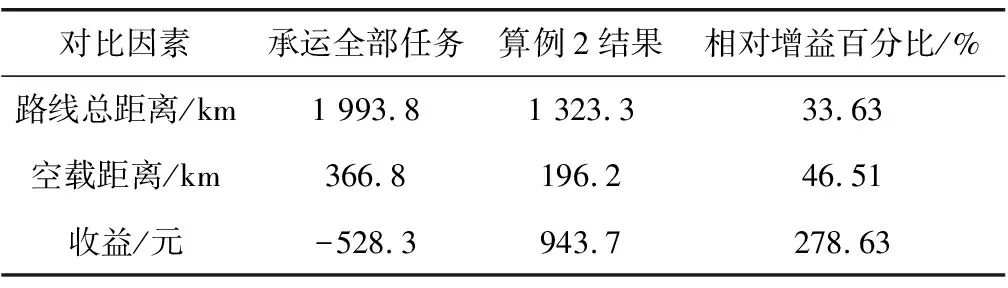
表10 结果对比Table 10 Comparison of results

综上可知，当不考虑线路间的协同效应而盲目选择增加托运任务，可能会增加承运人的运输成本，形成不合理的运输方案。因此，笔者所提模型和基于托运任务协同效应的求解策略可以帮助承运人在现货市场选择合适的托运任务，以实现承运人收益最大化。

4 结 语

笔者以承运人收益最大化为目标，以车辆最大装载货运量和最大行驶距离为约束条件，构建了零担物流选包和车辆路径优化的数学模型，提出了一种解决承运人选择市场上托运任务组合包的协同效应策略，并用2个算例验证了所建立模型及基于托运任务协同效应的求解方法的有效性和可行性。算例1中协同效应策略与反向精英粒子群算法求解方案相同，但协同效应策略运算时间仅需120.6 s，较后者减少1 775.1 s，求解时间缩短93.64%。扩大算例规模后，二者求解时间增加。在求解质量相同情况下，协同效应策略耗时148.6 s，反向精英粒子群算法则需4 125.9 s，后者运算时间增加96.4%。

通过计算结果可知，笔者提出的协同效应策略，不但可以快速的帮助承运人找到满意的现货市场托运任务组合，而且在求解结果相同的情况下，计算时间更少。所以本文研究成果求解可搭载零担物流组合包的选取问题具有一定的理论和应用价值。