综合小波分解和BP神经网络的交通小区生成交通短时预测
赵 顗,沈玲宏,马健霄,邱烜利
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
0 引 言
准确预知城市道路网未来短时交通状态是提前优化交通管理措施的基础,如提前发布道路网状态信息、实行超前交通诱导、调整信号协调控制方案等,从而提高城市道路智能化管理水平和道路网通行效率。但道路网未来短时交通状态受多方面因素影响,包括路网结构、当前信号控制方案、个体化出行特征等,其中各地块短时发生和吸引的交通生成量更是会直接影响到路网中的交通总量和交通分布状态。因此,有必要对各地块或交通小区的生成交通进行精确地短时预测,从而更好地掌握城市道路网未来短时交通状态。
现有短时交通预测主要以高速公路、一般公路和城市快速路为研究对象[1]。公路短时交通预测研究主要是预测交通流量[2]、出行时间[3]、延误时间[4]和行驶速度[5]等。城市道路短时交通预测研究主要是对交叉口排队长度[6]、路网交通拥堵[7]和各路段交通流量[8]等进行预测,对城市路网短时交通进行预测的研究成果较少,主要原因是城市道路网受干扰因素较多。
近年来,国内外涌现出的短时交通预测模型总体上可划分为基于统计分析的预测模型、基于非线性理论的预测模型、基于仿真的预测模型、基于知识发现的智能预测模型和基于混合理论的组合预测模型这5类[10]。B.L.SMITH等[11]提出了非参数回归模型,并与历史平均模型进行对比,验证模型的有效性;贺国光等[12]提出了基于小波分解和重构的短时交通预测方法;彭勇等[13]基于实际道路驾驶习惯的车辆跟驰策略,建立了连续性元胞自动机交通流仿真模型,并用实测数据验证了该模型的合理性;B.L.SMITH等[14]将BP神经网路应用于短时交通流预测研究;殷礼胜等[15]提出了一种整合移动平均自回归(ARIMA)模型和遗传粒子群算法优化小波神经网络(GPSOWNN)相结合的预测模型和算法。这些预测方法都有各自的优劣,而组合预测算法可根据不同模型优缺点进行组合以此提升模型预测精度,因此在短时预测方面得到关注。
基于现有研究进展,笔者拟采用组合预测算法探讨交通小区生成交通的短时预测方法。YANG Wen等[16]指出:相对于单个神经网络,使用小波变换对非线性时间序列先分解再预测能提高预测精度;WEI Yongtao等[17]提出:不同时间尺度上的流量变化是由不同网络机制引起的,小波变换能较好捕捉不同网络机制引起的流量相关结构。考虑到交通小区内包含有住宅、商业、教育、办公等不同用地性质建筑,而各类型建筑所生成的交通变化规律存在显著差异,笔者拟结合小波函数和BP神经网络模型对交通小区的生成交通进行分解后再预测,以提高交通小区生成交通短时预测精度。
1 交通小区交通数据采集
本研究使用高清智能卡口系统采集江苏溧阳主城区交通数据,通过车牌识别获取车辆行驶轨迹,从而提取车辆出行起终点信息。笔者选取江苏溧阳两个不同用地性质的交通小区作为研究对象,使用MySQL数据库筛选起终点位于目标交通小区交通量,获取交通小区生成交通量(包括发生交通量和吸引交通量)。
其中:1号交通小区是燕山南路—游子吟大道—育才南路—燕湖路围合范围,建筑以住宅用地为主,包括部分沿街商业和酒店,面积共计0.45 km2;2号交通小区是永平大道—昆仑南路—燕鸣路—南大街围合范围,建筑类型包括综合商业体、行政办公和教育建筑,面积共计0.42 km2。
采集时间为连续8 d,以15 min作为数据统计间隔,即每个交通小区可获取768条交通发生和交通吸引数据。两个交通小区的原始生成交通量数据如图1、 2。

图1 1号交通小区交通量数据Fig. 1 Traffic volume data of No.1 traffic zone
由两个交通小区原始生成交通量可看出:1号交通小区的早高峰为07:30—08:30,晚高峰为17:00—18:00,白天非高峰时段15 min发生和吸引交通量基本均不高于60辆;2号交通小区的早高峰为07:30—08:30,吸引交通的晚高峰为17:00—18:00,发生交通量不存在明显晚高峰时段,白天非高峰时段15 min的发生和吸引交通量基本不低于100辆。可见,两个交通小区短时生成交通特征存在显著差异。
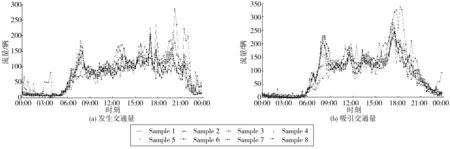
图2 2号交通小区交通量数据Fig. 2 Traffic volume data of No.2 traffic zone
2 短时预测模型构建
2.1 小波分解和BP神经网络基础理论
2.1.1 小波分析理论
小波函数基本思想是将原信号分解为一系列不同尺度的子序列。小波分解主要任务是构建标准化正交基,在该正交基下对信号进行分解,以便更好的提取信号特征;小波分解适用于非稳定信号,可用于信噪分离和提取弱信号。
在多尺度变换中存在多种小波函数,常见类型包括Haar小波、Mexican hat小波、Morlet小波和Daubechies(dbN)小波,一般根据小波函数自身的支撑集、正交性和消失矩等因素确定分析对象选用的小波函数。笔者使用小波函数对交通小区短时生成量进行多尺度分解,双正交小波基能放松正交性的要求保持线形相位,有利于实现小波分解的精确重构,紧支小波基能在离散小波分解过程中提供系数有限的、更实际的FIR滤波,因此需选择双正交性和紧支撑集的小波函数,满足需求的小波函数包括“Haar”、“dbN”、“coifN”和“symN”小波。其中:N代表小波函数的消失矩,消失矩越大其支撑长度就越长,对应的滤波器越平坦,即小波函数的消失矩大小决定了逼近信号能力。coif小波最大消失矩为5,随机选择一天出行交通量使用满足条件小波函数进行消失矩为5的2层分解,分解逼近信号如图3。
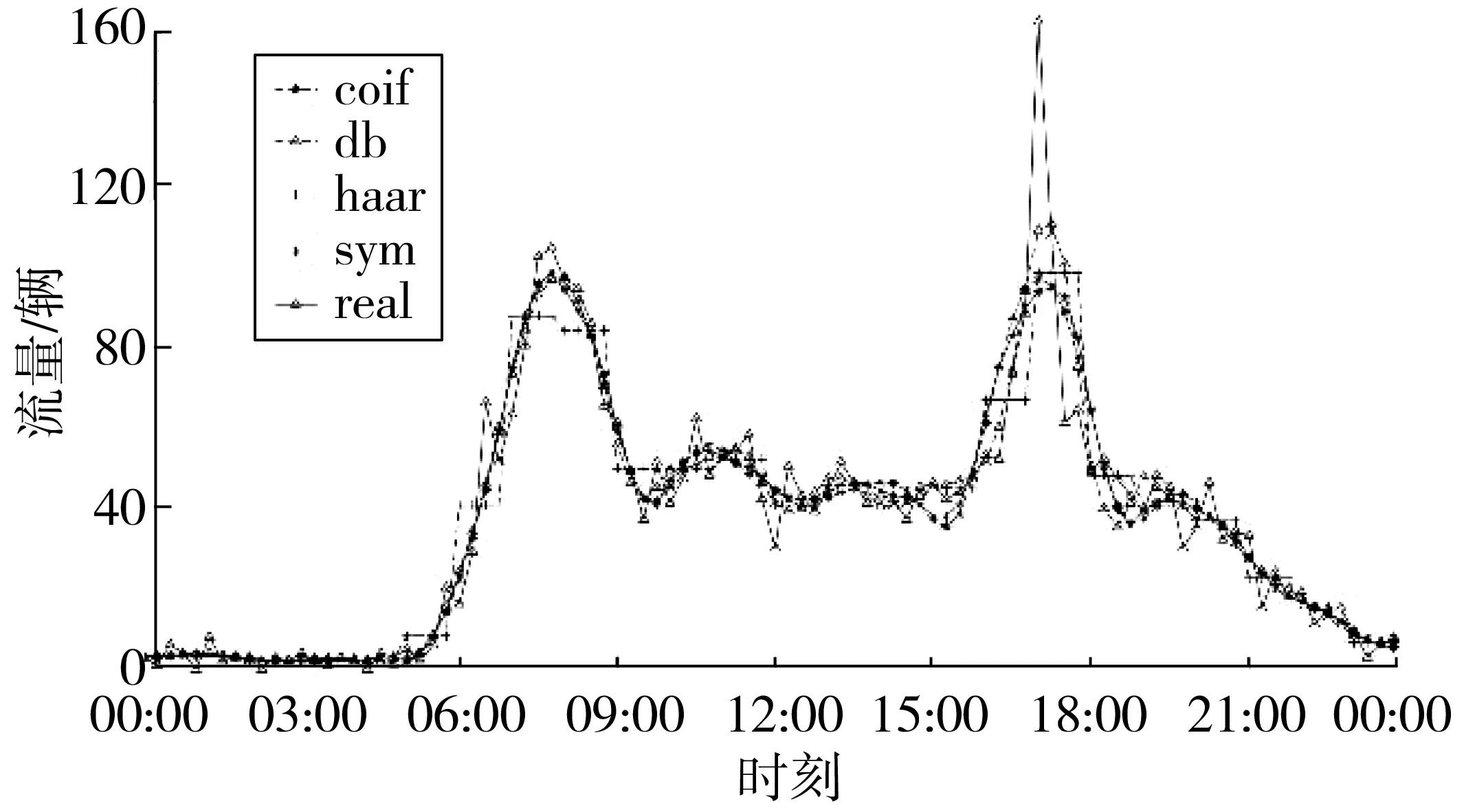
图3 不同小波函数低频逼近对比Fig. 3 Comparison of low frequency approximation of different wavelet functions
可见,haar小波存在严重的数据损失,coif小波和sym小波在低频逼近部分很相似,db小波能更好的逼近信号,尤其是在晚高峰时期比其他小波函数处理的好。因此,本研究将选择dbN小波对交通小区的短时生成交通量进行分解。
2.1.2 BP神经网络
神经网络可模仿人脑学习过程特征,进行分布式并行信息处理的算法数学模型[18]。神经网络模型包括BP神经网络、径向基(RBF)神经网络、感知器神经网络等多种类型。其中,BP神经网络又称误差反向传播网络,具有自学习、自适应特点,能以任意精度逼近非线性关系,在神经网络中应用广泛。B.L.SMITH等[14]等首次将BP神经网络应用于交通流短时预测中,刘静等[19]和LIU Zhongbo等[20]分别证明在短时交通流预测中BP神经网络预测精度优于RBF神经网络,在实际工程中具有良好的适用性。
BP神经网络主要是由输入层、隐含层和输出层构成,其中隐含层节点数的选择、训练数据规模、隐含层和输出层传递函数的选择对BP神经网络预测精度有着较大影响。隐含层节点数太少,不能构建复杂的映射关系,使得BP神经网络预测精度较低;当节点数过多时,学习时间增加易出现过拟合现象。传递函数用于输入和输出之间转换,也称为激活函数。传递函数通常分为线性传递函数和非线性传递函数两种类型;MATLAB中提供Logsig函数、Tansig函数和Purelin函数这3种传递函数,通常隐含层传递函数选用Logsig函数或Tansig函数,输出层节点传递函数选用Tansig函数或Purelin函数。
Logsig函数关系如式(1):
(1)
Tansig函数关系如式(2):
(2)
Purelin函数关系如式(3):
y=x
(3)
2.2 组合预测模型
2.2.1 模型构建
综合小波分析和BP神经网络的组合预测模型的逻辑结构如图4。
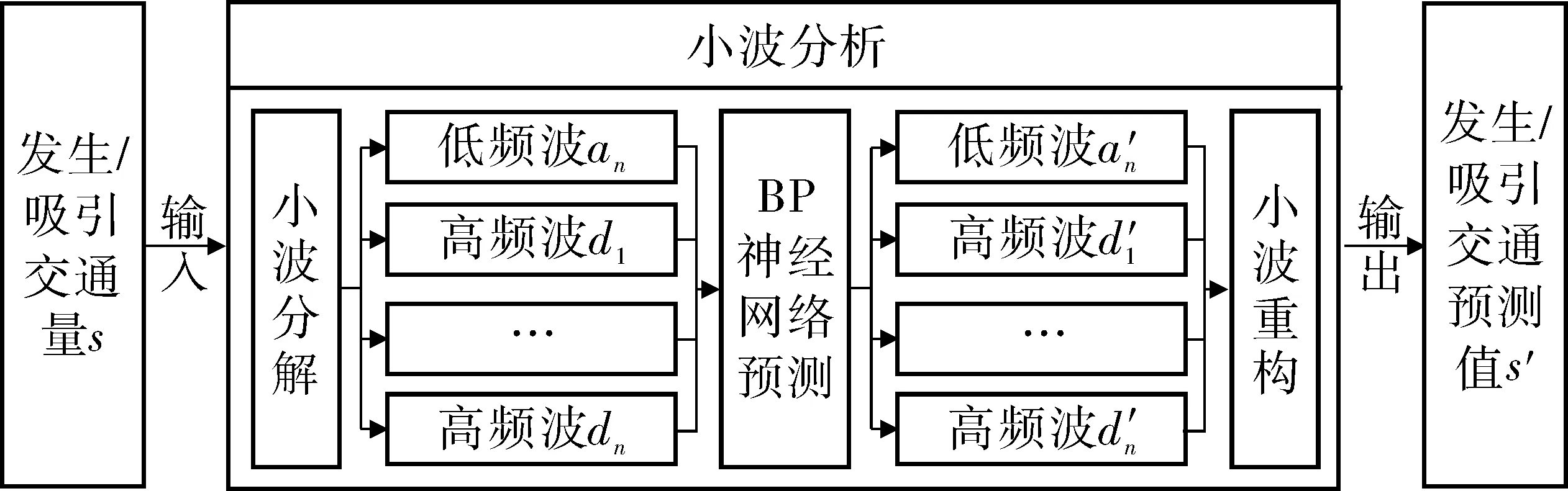
图4 组合预测模型逻辑结构Fig. 4 Logical structure chart of the combined forecasting model
在组合算法中,小波分析能将信号分为低频近似和高频细节两个部分,有效捕捉信号的时间位置和频率信息,对不同频率的时间序列进行特征提取,将交通小区生成交通量s剥离成不同类型的出行交通量an和di(i=1, 2,…,n);BP神经网络是短时预测的核心算法,用于对分解后的各波形进行短时预测,得到预测值a′n和d′i(i=1, 2,…,n);最后使用小波分析的波形重构得到交通小区生成交通量短时预测值s′。
在组合预测模型中,使用dbN小波函数进行数据分解,使用BP神经网络进行预测。本研究中,使用单隐含层的BP神经网络进行短时预测,直接确定参数有训练次数、训练目标为、学习概率。通过对比分析确定小波分解中的N值和分解层数及BP神经网络中的传输函数、训练函数和节点个数。
2.2.2 参数设置
1)评价准则选取
为评价预测结果的性能,采用均方误差(MSE)和决定系数(Rsquare)作为评价指标,指标定义如式(4)、(5):
(4)
(5)
式中:Yactual为时间序列的实际交通流数值;Ypredict为时间序列预测值;Ymean为时间序列实际交通流均值;n为预测样本长度。
2)小波分解层数设置
在对交通小区生成交通量进行分解时,主要参数是消失矩N和多尺度分解层数,其中消失矩决定低频细节分量光滑程度,分解层数则影响着预测精度。笔者在保证分解后各子序列均较为平滑且不存在严重信号损失同时,尽量减少模型复杂度,经过多次实验对比分析选择对交通小区生成交通量使用db4小波进行3层分解。以1号小区吸引交通量为例,其分解结果如图5。

图5 1号交通小区吸引交通量小波分解Fig. 5 Wavelet decomposition of the attracted traffic volume of No.1 traffic zone
3)传输函数及节点数设置
隐含层节点和输出节点的传递函数通过对比试验确定,随机选择统计数据中一天的生成交通量,使用BP神经网络进行短时预测,除传递函数以外,其他参数均保证一致,对比不同传递函数下预测的均方误差,选择均方误差最小的组合传递函数。不同传递函数下预测得到的均方误差值如表1。

表1 隐含层、输出层节点函数均方误差Table 1 Mean square error table of node functions in hidden layer and output layer
结果表明:隐含层节点和输出层节点的传递函数均选Tansig函数时预测误差最小。同理可确定训练函数为动量反传和动态自适应学习率的梯度下降BP算法。隐含层节点个数将在后续预测过程中根据预测精度需求进行选择。
3 预测效果分析
3.1 实验分组及参数设置
笔者将通过对比实验检验构建模型对交通小区生成交通的短时预测精度,实验组划分为模型组和对比组两组,其中模型组采用文中提出的综合小波分解和BP神经网络的组合预测模型进行短时预测,对比组采用单一的BP神经网络模型进行短时预测。实验组的主要参数设置如下:
1)小波分解函数设置:小波函数选择db4,分解层数为3;
2)BP神经网络模型基本参数设置:训练次数为1 000,训练目标为1E-7,学习概率为0.000 1;
3)BP神经网络模型学习函数设置:隐含层和输出层节点传递函数均选择Tansig函数,训练函数选择Traingdx,权重学习函数选择Learngdm;
4)BP神经网络模型隐含层和神经元数量设置:设置一个隐含层,隐含层神经元数量需通过训练和测试确定,神经元数量可变范围为[5,15];
5)实验数据设置:将交通小区前7 d的生成交通量作为训练样本,将第8天的生成交通量为预测目标。
3.2 预测结果分析
针对模型组和对比组中BP神经网络隐含层的神经元,通过设置不同的神经元数量,对比预测精度选择最优神经元数量。以1号交通小区吸引交通量为例,经对比分析得出:当设置9个神经元时,低频波a3和高频波d2的预测均方误差最小,分别为4.503和5.211;当设置8个神经元时,高频波d1和d3的预测均方误差最小,分别为8.590和7.211;对比组中,当设置8个神经元时,直接用BP神经网络进行短时预测的均方误差最小。模型组预测中,1号交通小区吸引交通量进行小波分解后各子序列的短时预测结果如图6。
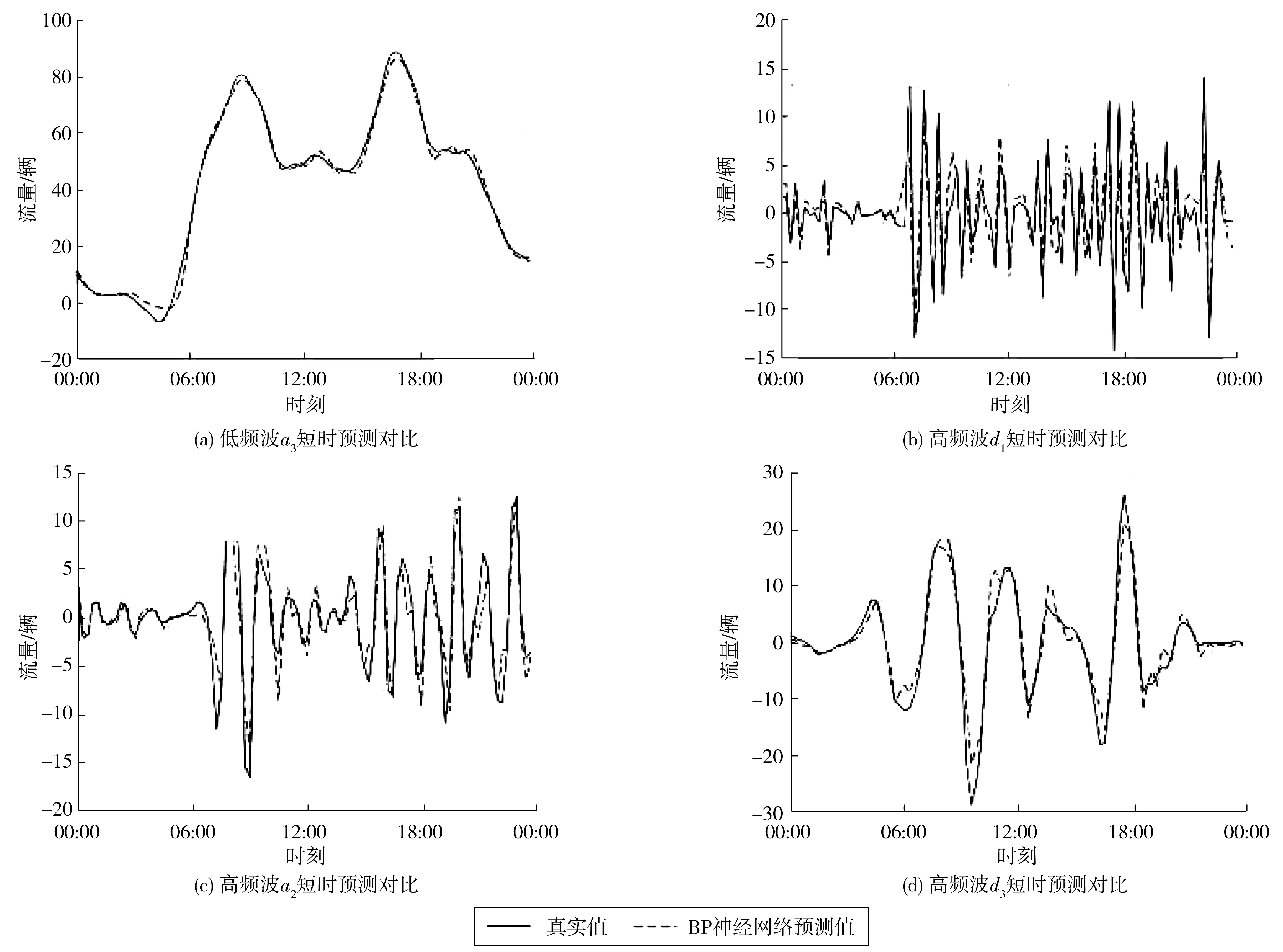
图6 1号交通小区吸引交通量各子序列短时预测结果Fig. 6 Short-term prediction results of subsequences of the attracted traffic volume in No. 1 traffic zone
将各子序列的预测值进行小波重构,得到1号交通小区吸引交通量短时预测值;对比组预测中,根据构建的BP神经网络模型直接对1号交通小区吸引交通量进行预测。模型组和对比组针对1号交通小区吸引交通量最终预测结果如图7。
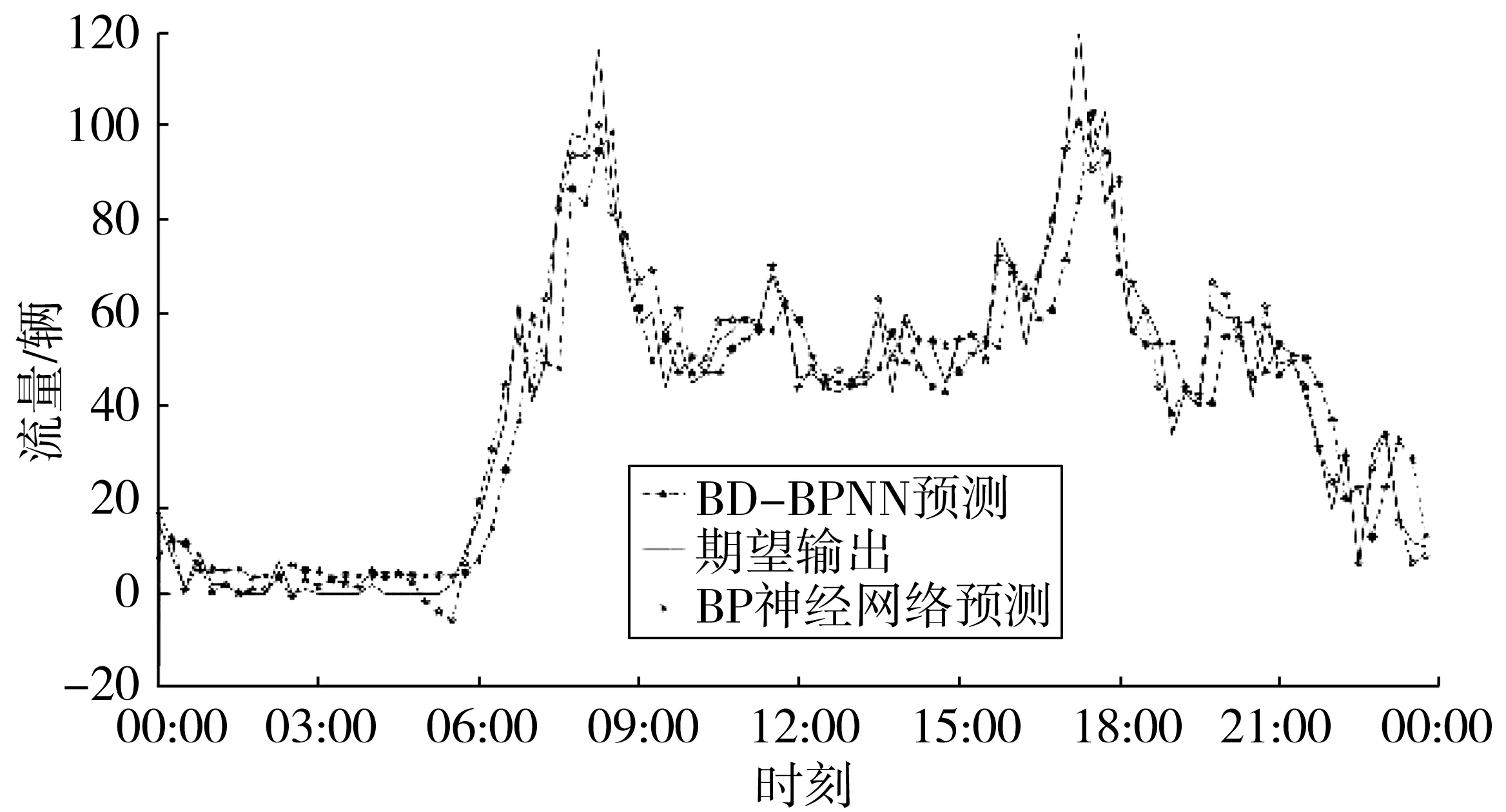
图7 1号交通小区吸引交通量短时预测对比Fig. 7 Comparison chart of short-term forecast of the attracted traffic volume of No.1 traffic zone
同理,对2个交通小区的发生交通量和吸引交通量分别采用模型组和对比组两种预测方式进行预测,利用均方误差(MSE)和决定系数(Rsquare)度量两种预测模型的预测结果。两种预测模型对不同交通小区生成交通量的短时预测结果如表2。根据表2可知:相对于单独使用BP神经网络对交通小区的发生和吸引交通量进行短时预测,本研究提出的综合小波分解和BP神经网络的组合预测模型预测精度更高。以MSE作为衡量指标,对不同交通小区,当采用组合预测模型进行预测时预测精度提高幅度最高可高达87%;以Rsquare作为衡量指标,对于不同交通小区,当采用组合预测模型进行预测时预测精度提高幅度最高可高达25%;且对任一交通小区,无论是预测发生交通量还是吸引交通量,组合预测模型的预测精度都高于单独使用BP神经网络时的预测精度。
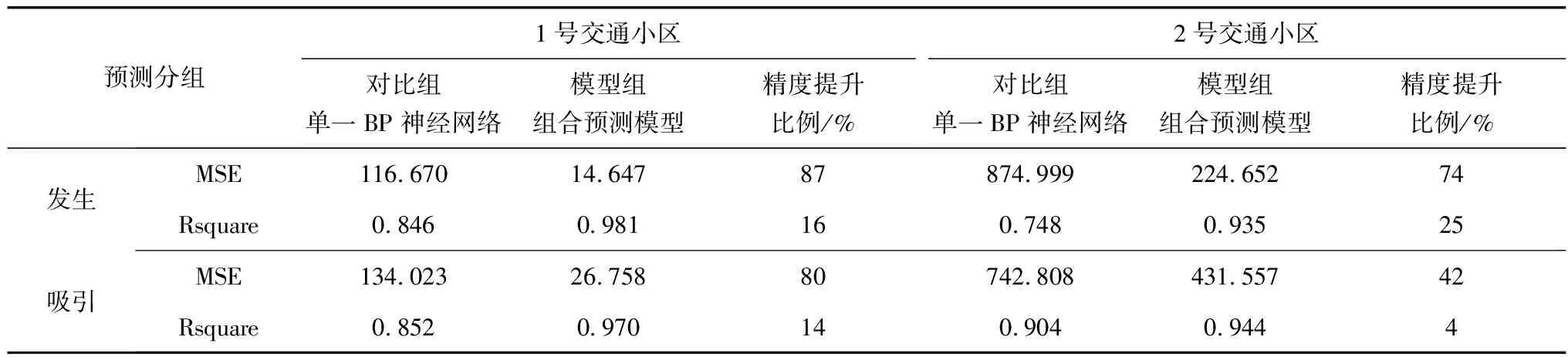
表2 交通小区生成交通量短时预测对比分析Table 2 Comparison and analysis of short-term forecast of traffic volume generated by traffic zone
4 结 论
笔者针对交通小区生成交通的短时预测需求,提出综合小波分析和神经网络的组合预测模型。经对比研究,采用dbN小波函数用于对交通小区的生成交通数据进行小波分解,BP神经网络用于对分解后的各频段波形进行短时预测,经小波重构后获得交通小区生成交通的短时预测结果。为检验构建模型的预测精度,将独立使用BP神经网络模型作为对比预测模型。采集实际交通小区的真实交通生成量,量化分析确定dbN小波函数的分解层数、BP神经网络的传输函数和节点数等参数,以均方误差(MSE)和决定系数(Rsquare)为度量指标,通过实验对比构建预测模型和对比预测模型的预测精度。实验结果表明:对不同类型的交通小区,对交通发生量和交通吸引量,综合小波分析和神经网络组合预测模型比单独使用BP神经网络预测模型的预测精度都要更好,说明文中构建的预测模型有效。
受限于数据规模,笔者仅对住宅为主的交通小区和商业为主的交通小区进行了验证分析,模型对其它类型交通小区生成交通短时预测的有效性还有待未来进一步检验。此外,在对小波函数和BP神经网络模型进行参数标定时,并未对逐一对各参数进行最优化检验,未来还可进一步深入研究。

