基于改进樽海鞘群算法的卸车调度优化

李长安，赵德隆，王国勇，吴忠强，张立杰

(1. 燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004; 2 .燕山大学 电气工程学院， 河北 秦皇岛 066004； 3.燕山大学 河北省重型机械流体动力传输与控制重点实验室，河北 秦皇岛 066004； 4. 神华天津煤炭码头有限责任公司，天津300457)

0 引 言

以往的港口作业调度多为人为决定，调度模式缺乏科学性，调度效率低，应变能力不足，经常造成火车长期滞留和煤炭积压等问题，削弱了港口的市场竞争力，是亟待解决的关键问题。

港口调度问题具有复杂、随机、多约束和多目标等特点，许多经典优化算法已被成功的应用到港口调度问题中。B. SKINNER等[1]以遗传算法为基础，结合使用了路径规划的方法将港口集成调度作业分组进行优化；张新宇等[2]建立双向通航港口调度优化模型，用多目标遗传算法寻找最优解；曾建智等[3]在对分段堆场调度的研究中，应用双层遗传算法优化分段出场时间和停放位置，并使用启发式规则搜索分段调度路径；陈文[4]构建了泊位岸桥联合调度模型，使用萤火虫算法求解调度方案；王诺等[5]将改进模拟植物生长算法应用于优化港口调度问题；陈红梅等[6]建立M/M/S排队模型研究卸车调度，并用实际港口实验验证了模型的有效性；刘文远等[7]构建了关联堆场作业动态卸车联合调度优化模型，使用禁忌搜索算法实现最优卸车调度；邰世文等[8]以卸车效率最大和列车在港时间最短为目标，设计了采用仿真推演策略解码的遗传算法求解此多约束多目标优化模型。

以港口的卸车作业为研究对象，以载煤列车在港滞留总时间最短为研究目标，构建了考虑多煤种、火车调度时间、工作机械可用性、作业流程可达性及其相互约束关系等因素的卸车作业模型。采用基于改进樽海鞘群算法(improved seyedali seyed andrew，ISSA)求解。改进的樽海鞘群算法引入自适应惯性权重，提高了算法收敛速度；引入柯西变异策略，提高了算法寻优能力，得到了到港列车的优化翻卸调度顺序，减少了列车在港等待时间，达到了提高港口工作效率，节省列车等待成本的目的。

1 卸车调度数学模型

以优化火车总在港时间为目标，卸车调度的数学模型为：①火车集P={p1,p2,…,pn}，pi表示第i列火车，i=1,2,…,n；②翻车机集C={c1,c2,…,cm}，cj表示第j台翻车机，j=1,2,…,m；③堆垛集S={s1,s2,…,sq}，sk为第k个堆场垛位，k=1,2,…,q。

火车pi开始被翻车机cj作业的时间为：

Sij=ai+wi+dij

(1)

式中：ai为火车pi的到港时间；wi为火车pi的等待时间；dij为火车pi与翻车机cj的对接所用时间。

第i列火车的牵空离港时间为：

li=Sij+Fij+Bij

(2)

式中：Fij为翻卸作业所消耗时间；Bij为火车pi与翻车机cj的拆离所用时间。

火车pi的等待时间为：

(3)

式中：Xij为火车pi是否在翻车机cj上作业；lα为火车pi在对应翻车机上开始作业的时间(等同于前一列火车完成作业的牵空时间)。

目标函数为列车总在港时间最少[7]：

(4)

约束条件为：

(5)

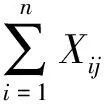
2 樽海鞘群搜索算法

樽海鞘群搜索(seyedali seyed andrew，SSA)算法是2017年由S. SEYEDALI等[9]提出的一种新型智能优化算法，是受到樽海鞘群体行为特征启发而开发的算法。SSA算法中樽海鞘以“链”的方式分布，群体中含有两种角色：领导者和跟随者，领导者是处于群链最前端的背囊生物，而剩下的生物为跟随者，领导者负责带领跟随者进行协调运动，在搜索空间中寻找更好的食物源作为群体运动目标[10]，两者在搜索过程中不断更新自己位置，不断向最优食物源移动。相比其他生物种群来说，樽海鞘群体中领导者对群体的影响力不高，领导者只直接影响紧挨着自己的第2个跟随者的位置更新，第2个影响第3个，由此类推，领导者对后面跟随者的影响力逐层递减，可以使得排在后面的跟随者在更新过程中保持多样性。

算法步骤如下：

1)初始化种群

xn=rand(N,D)×(u-l)+l

(6)

式中：xn=[xn1,xn2,…,xn1]T,n=1,2,…,N为第n只樽海鞘在搜索空间中的位置，N为樽海鞘群的规模；D为搜索空间维度，u=[u1,u2,…,uD]T为搜索空间的上限；l=[l1,l2,…,lD]T为搜索空间的下限。

2)领导者位置更新

(7)

式中:x1j(j=1,2,…,D)为领导者每一维的状态；Fj为食物所在位置；c2,c3为[0,1]内的随机数，作用是增强领导者位置更新的随机性，增强个体的多样性和加强全局搜索能力；c1为收敛因子，起到权衡种群勘探和开发食物源的作用，当其大于1时，算法进行全局搜索，当其小于1时，算法进行局部开发，得到精确的估计值，c1的取值通常是一个2～0的递减函数，表达式如式(8)：

(8)

式中：t为当前迭代次数；tmax为最大迭代次数。

3)追随者位置更新

(9)

式中：xmj(m=2,3,…,N)为第m个追随者第j维的位置。

3 ACSSA算法

针对SSA算法在函数寻优过程中存在的估计精度不高、收敛速度慢、容易陷入局部最优等问题，提出两点改进：①自适应惯性权重；②柯西变异策略，新算法记为ACSSA (adaptive cauchy SSA) 算法。

3.1 自适应惯性权重

张永等[11]提出了惯性权重线性下降策略并应用到WOA(whale optimization algorithm )算法中, 实验证明, 较大的惯性权重有利于粒子全局寻优，反之, 则利于局部开发、加快收敛速度。因此, 惯性权重对算法收敛速度和全局寻优能力都有重要影响，由于SSA在优化过程中是非线性变化的, 惯性权重线性下降策略无法体现实际的优化搜索过程, 又考虑到各搜索个体间的状态差异性, 为此笔者提出基于搜索个体当前状态的非线性自适应权重策略，将领导者位置更新表达式加入自适应权重，表达式为：

(10)

式中：g, h为常数；t为当前迭代次数。

将(10)式代入式(7)，得出领导者位置更新表达式为：

(11)

追随者位置更新表达式(9)加入反向非线性自适应权重，表达式为：

(12)

3.2 柯西变异策略

王永骥等[12]引入柯西变异策略并应用到PSO (particle swarm optimization) 算法中，有利于增加种群多样性以减小陷入局部最优的概率。为了提高SSA算法的寻优能力，笔者提出一种以当前最优樽海鞘位置为中心的随机柯西变异策略，协调全局搜索和局部开发能力，进而提高算法寻优能力，表达式为：

(13)

式中：xbestj为当前迭代过程中领导者第j位置，Cauchy(0,1)是服从标准柯西分布的随机数。

4 算法测试与分析

为了验证笔者所提出算法的优越性，选取5个标准测试函数将ACSSA与ASSA (adaptive SSA)、SSA算法性能进行比较。5个标准测试函数分别为：Ackley函数、Sphere函数、Quartic函数、Schwefel’s problem 22函数以及Griewank函数等，具体表达式和搜索空间如表1。种群规模n、迭代次数Tmax、粒子空间维数D统一设定为30、1 000、10。3种算法分别独立运行10次，并对运行所得的最优值、均值及方差进行比较，结果如表2。

表1 标准测试函数Table 1 Standard test functions

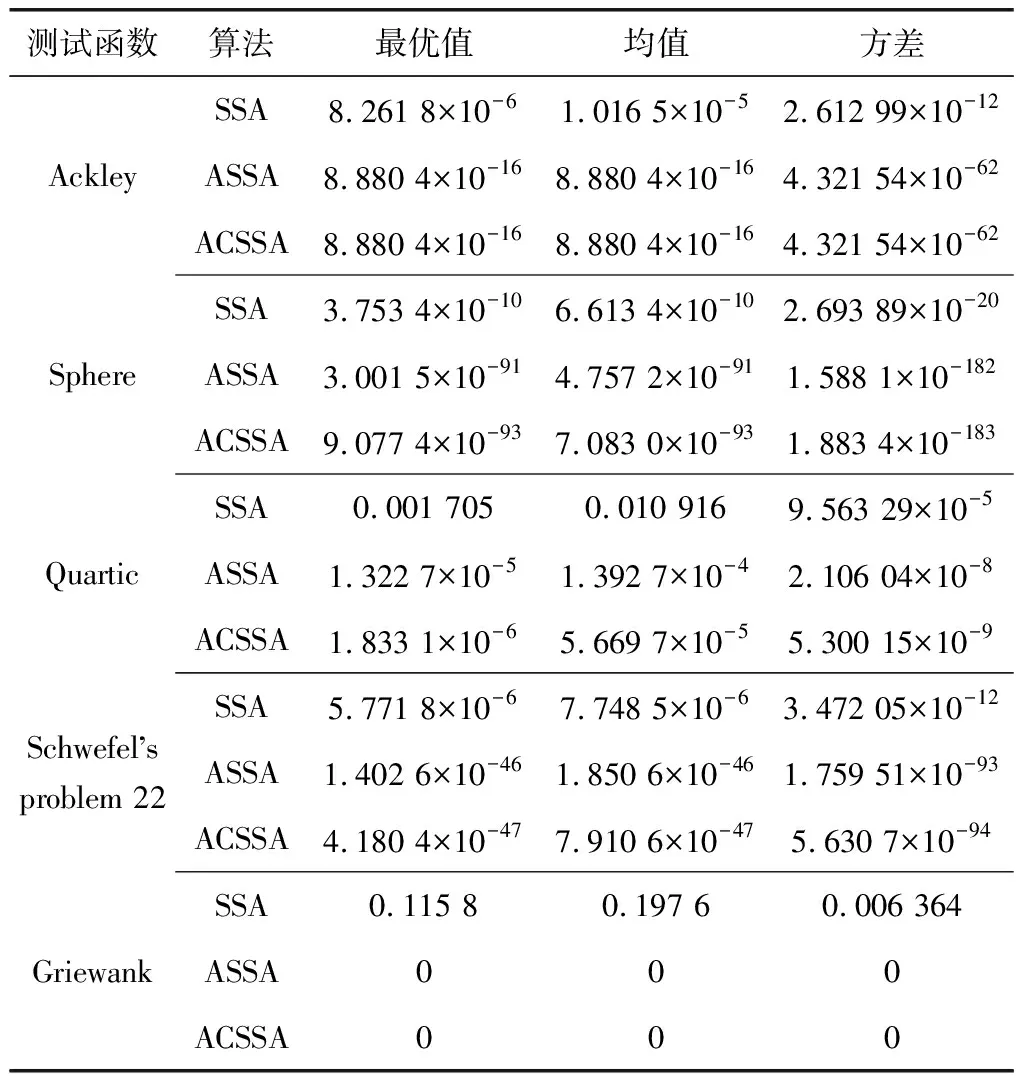
表2 3种算法估计精度Table 2 Estimation accuracy of three kinds of algorithms

从表2的最优值对比结果可以看出， SSA算法的最优值达到10-10， ASSA算法的最优值达到0，估计精度提高。从经典测试函数的均值和方差可以看出，SSA算法的均值和方差分别在10-5和10-11左右， ASSA算法的均值和方差分别在10-46和10-92左右，因此，ASSA算法具有较强的寻优能力和稳定性。从ASSA算法和ACSSA算法的对比结果可以看出，提出的自适应柯西变异策略对ASSA算法的估计精度略有提高。

下面对3种算法的收敛速度进行比较，将运行10次的适应度值取平均值，结果如图1～图5。

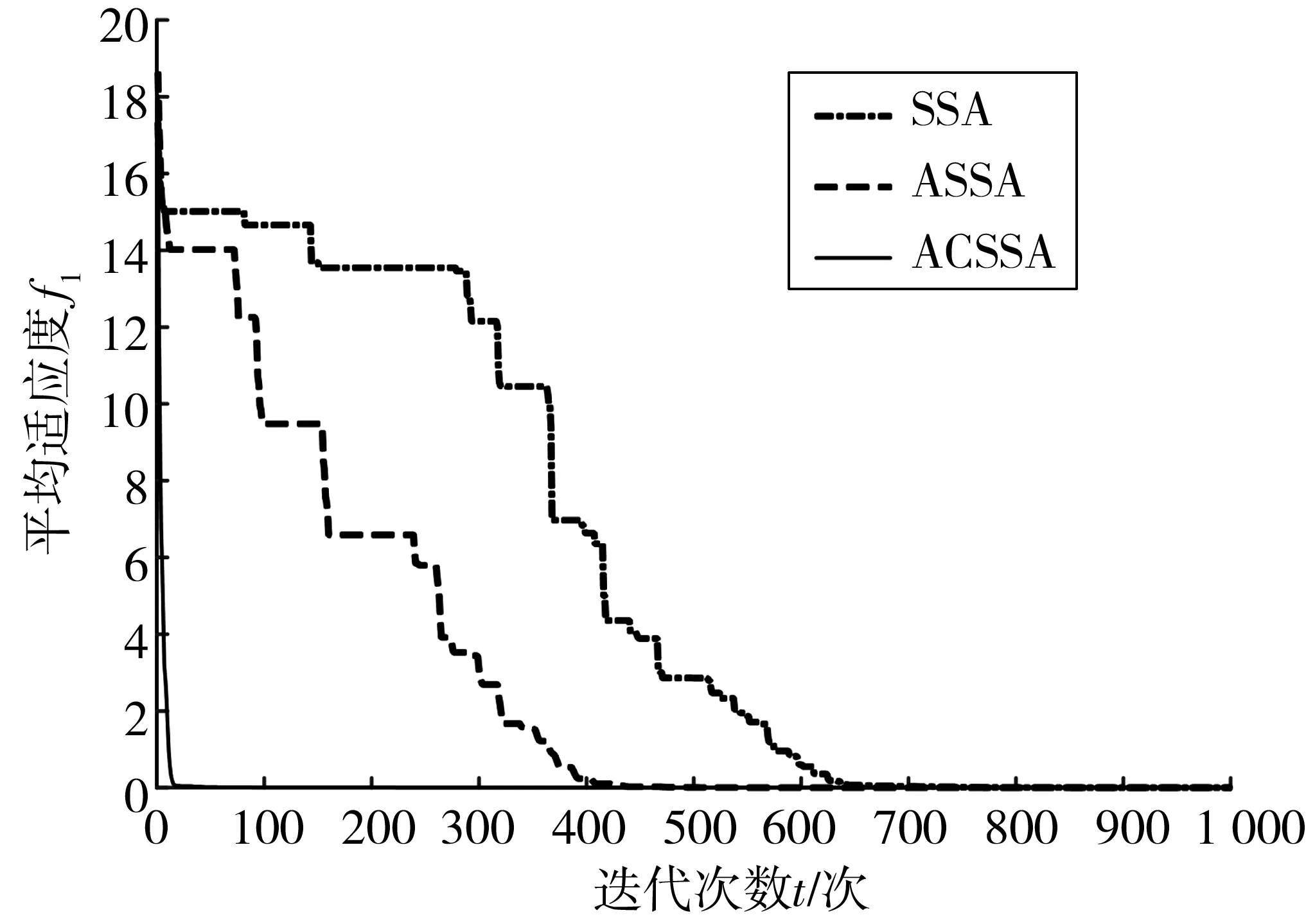
图1 Ackley函数Fig. 1 Ackley function

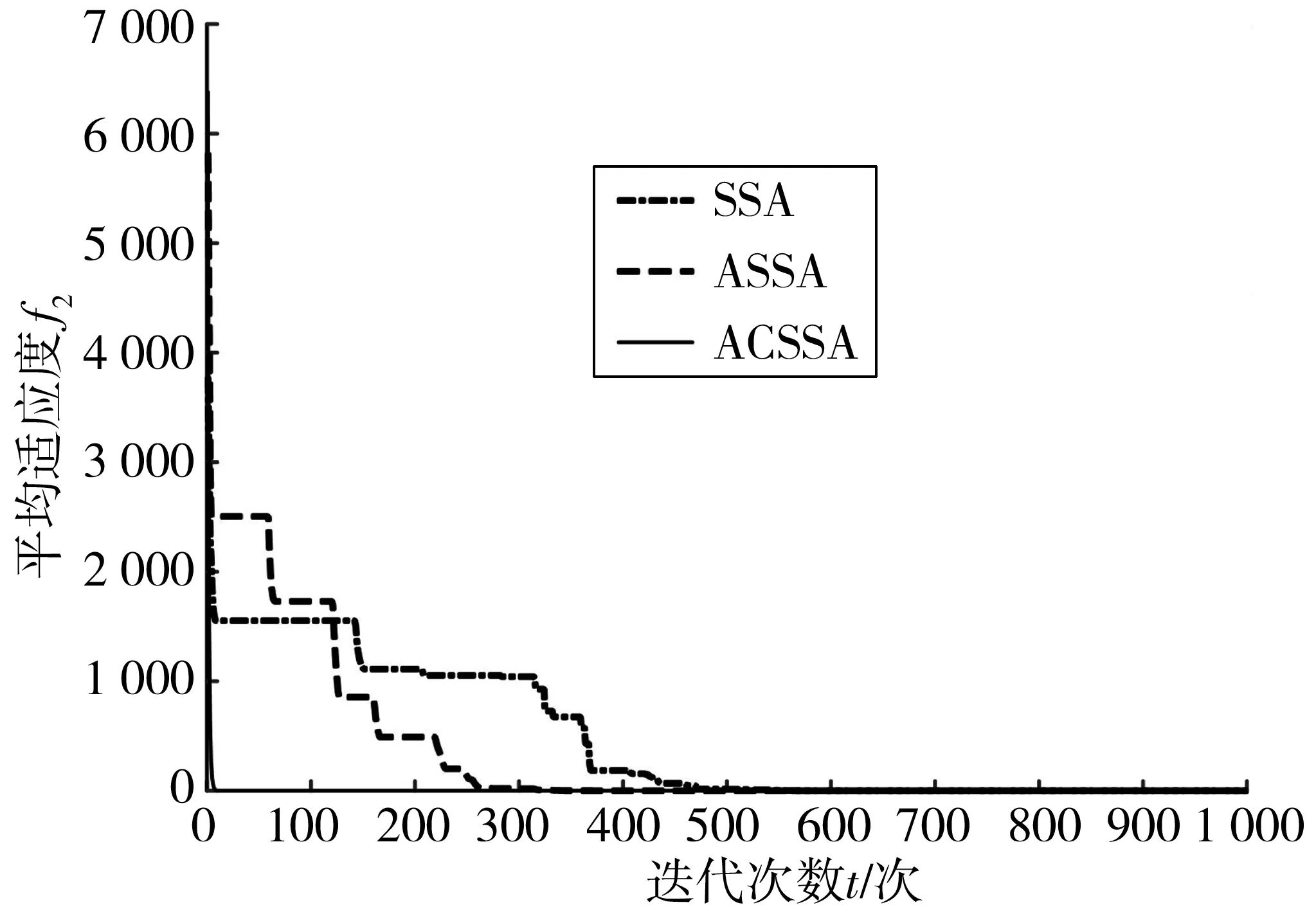
图2 Sphere函数Fig. 2 Sphere function

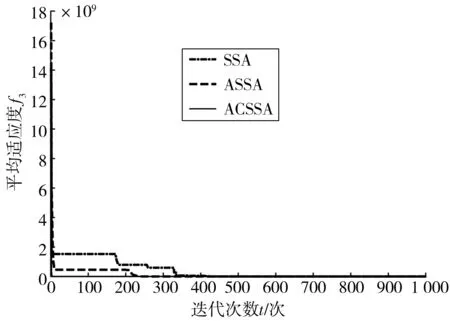
图3 Quartic函数Fig. 3 Quartic function

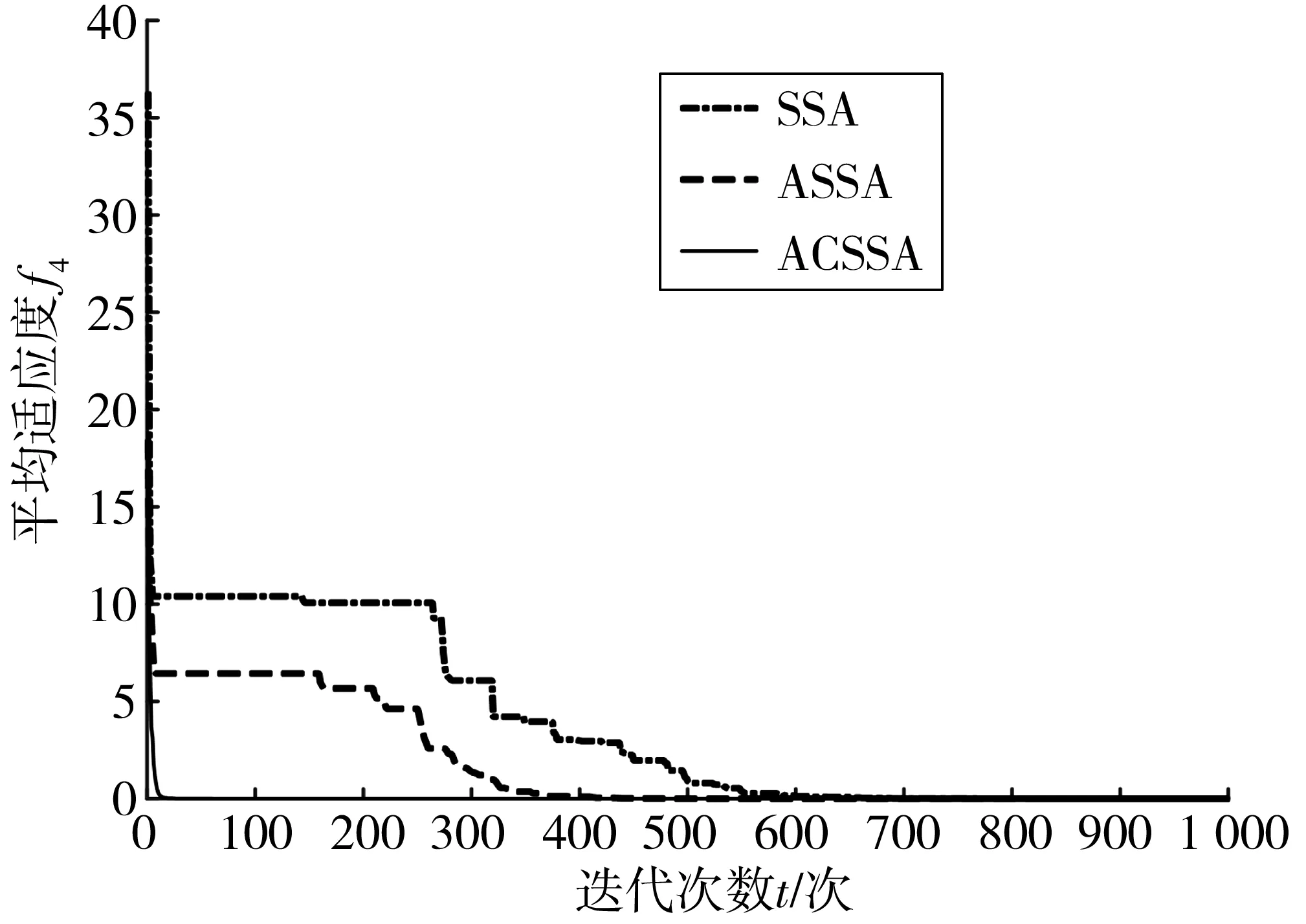
图4 Schwefel’s problem 22函数Fig. 4 Schwefel’s problem 22 function

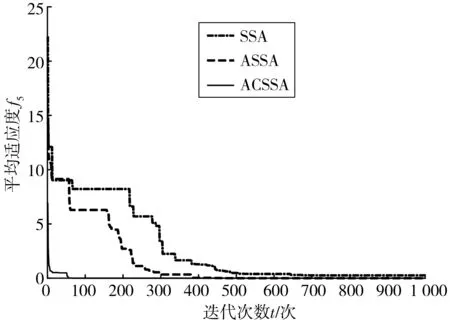
图5 Griewank函数Fig. 5 Griewank function

从图1～图5可看出， SSA算法迭代至少400次才可以达到收敛， ASSA算法迭代200～300次就能收敛，相比SSA算法收敛速度变快， ACSSA算法迭代20～50次就能收敛，收敛速度相比前两者有大幅提高。此外，如图5相比SSA算法对一些函数寻优容易陷入局部极值，ASSA算法与ACSSA算法不容易陷入局部最优，寻找全局最优解的能力增强。

将ACSSA算法与WOA算法、PSO算法进行对比，同样采用表1测试函数，种群规模n、迭代次数Tmax、粒子空间维数D统一设定为30、1 000、10。3种算法分别独立运行10次，并对运行所得的最优值、均值及方差进行比较，结果如表3。

从表3的最优值对比结果可以看出， PSO的最优值达到10-25， WOA最优值达到10-16， ACSSA最优值可以达到0，对于表中的测试函数，ACSSA的寻优精度优于前两种算法。从测试函数的均值和方差可以看出，PSO的均值和方差分别在10-10和10-19左右，WOA的均值和方差分别在10-10和10-20左右，而ACSSA的均值和方差分别在10-52和0左右，因此，ACSSA与PSO与WOA相比具有较强的寻优能力和稳定性。

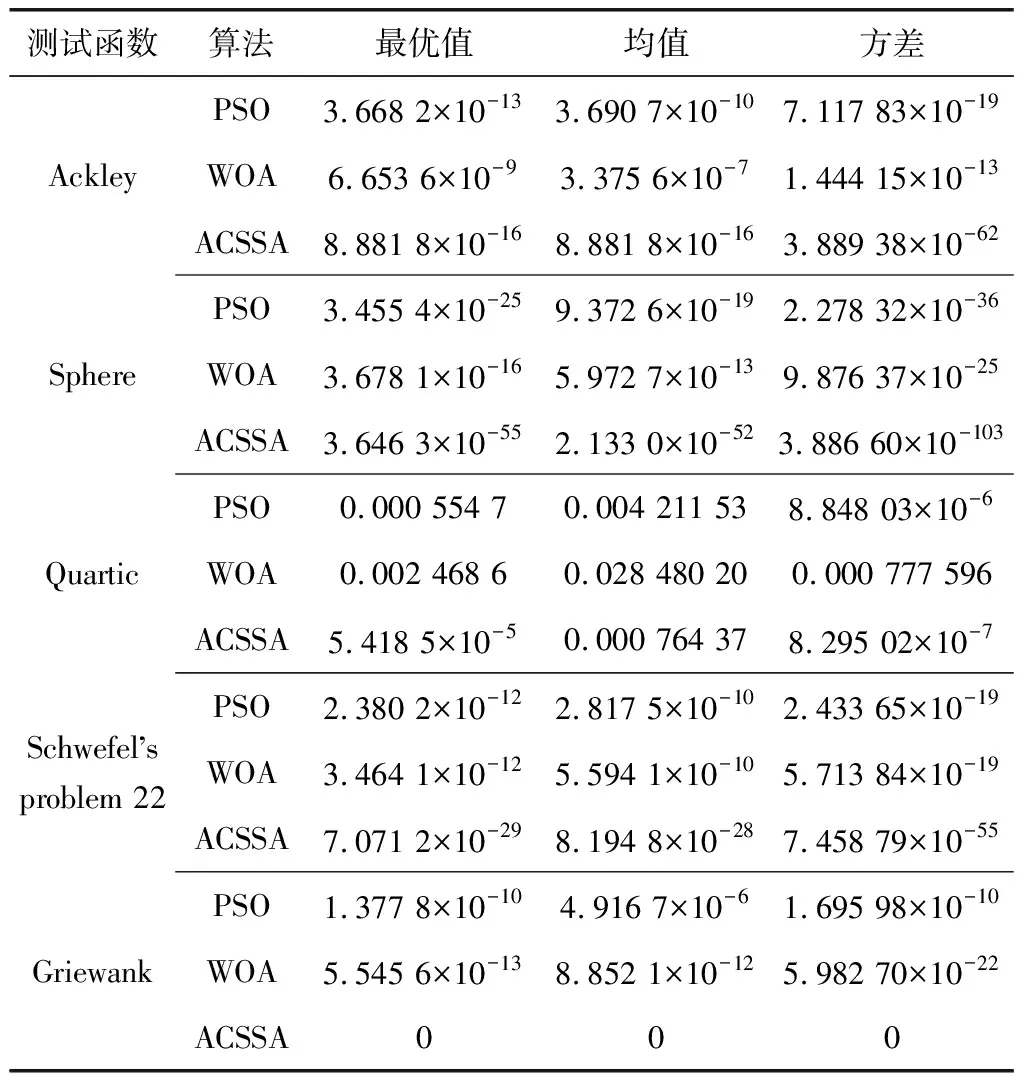
表3 ACSSA、WOA 和PSO的估计精度Table 3 Estimation accuracy of ACSSA, WOA and PSO

ACSSA、WOA 和PSO的收敛速度对比如图6～图10。

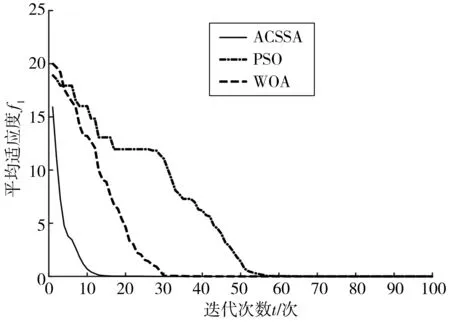
图6 Ackley函数Fig. 6 Ackley function

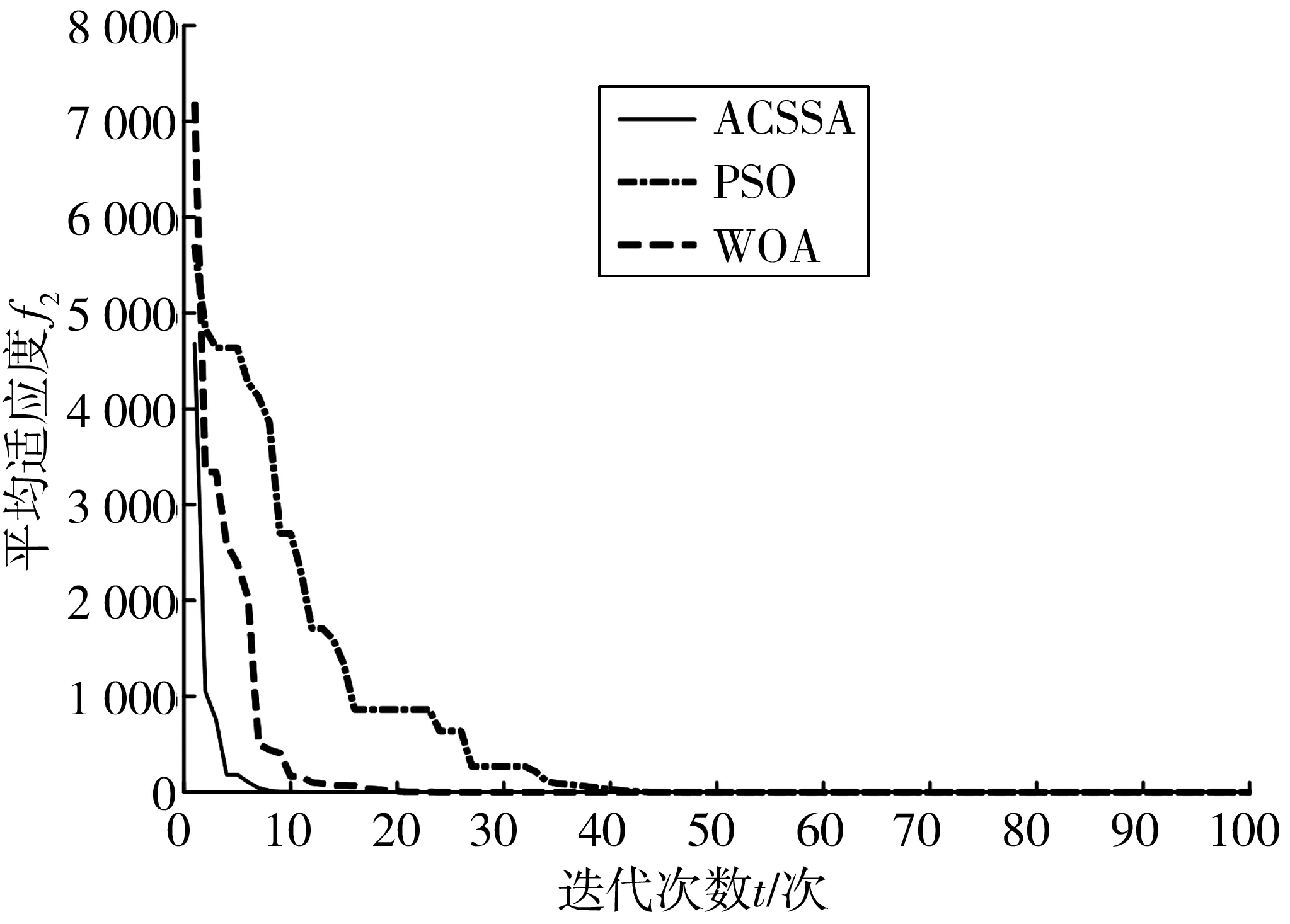
图7 Sphere函数Fig. 7 Sphere function

图8 Quartic函数Fig. 8 Quartic function

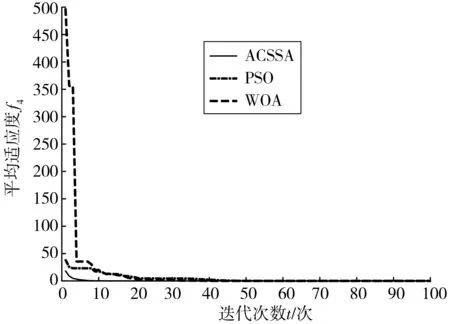
图9 Schwefel’s problem 22函数Fig. 9 Schwefel’s problem 22 function

从图6～图10可以看出， PSO迭代至少50次才可以达到收敛，WOA迭代20～40次能达到收敛，ACSSA迭代5～20次就能收敛，收敛速度相比PSO与WOA有大幅提高。

5 算 例

将改进算法应用到港口卸车调度中。港口卸车工序可描述为：火车运输煤炭至港口→经过专业化的翻车机卸车→通过皮带机转运→通过堆料机在堆场堆放。某港口目前有6条取装线，4台翻车机。 假设港口每个时间点驶入3辆列车进行卸车调度，其调度时间表及每列列车可选择的翻车机序号表，如表4(如6:30的列车1驶入港口后可选择的翻车机序号为1或2)，各列车在对应翻车机上卸煤所需的时间如表5，单位为min。

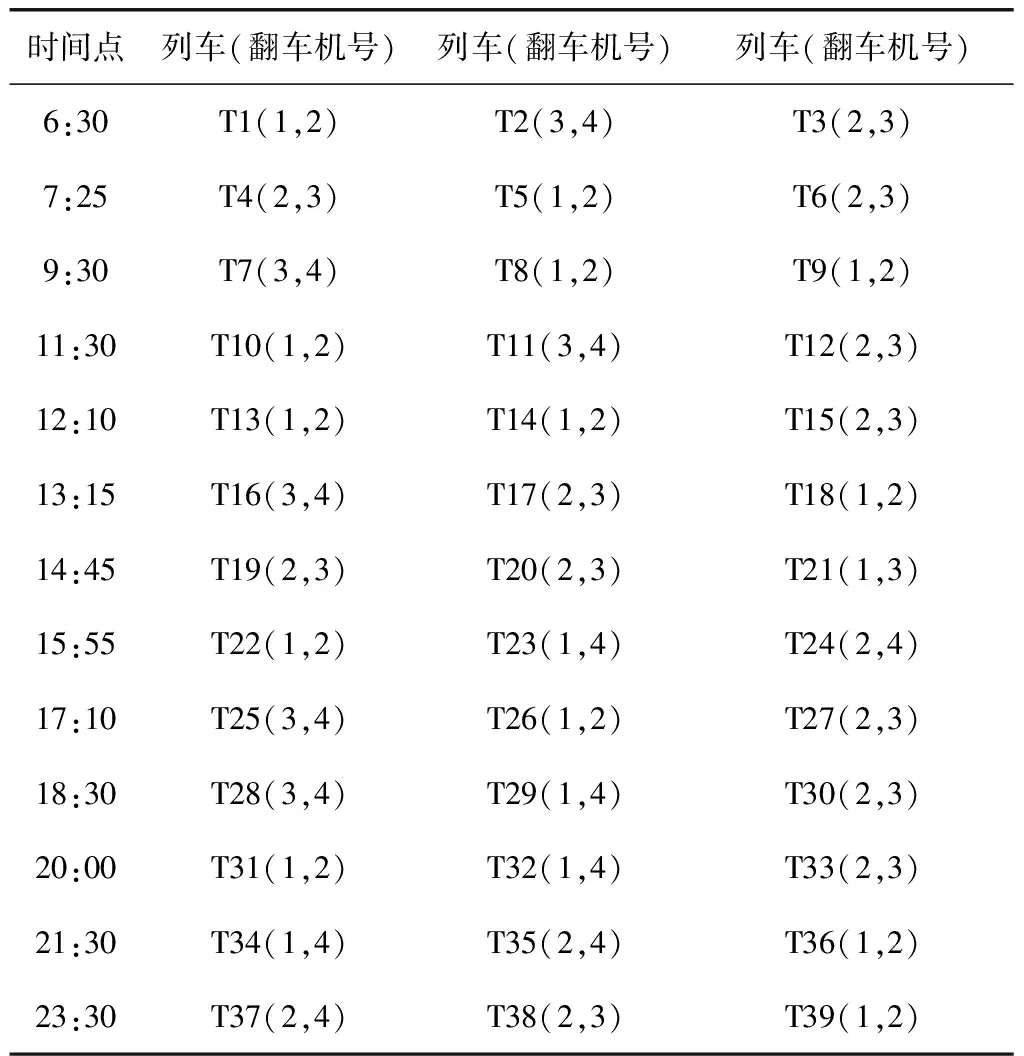
表4 列车调度时间及可选翻车机序号Table 4 Train dispatching time and optional dumper serial number

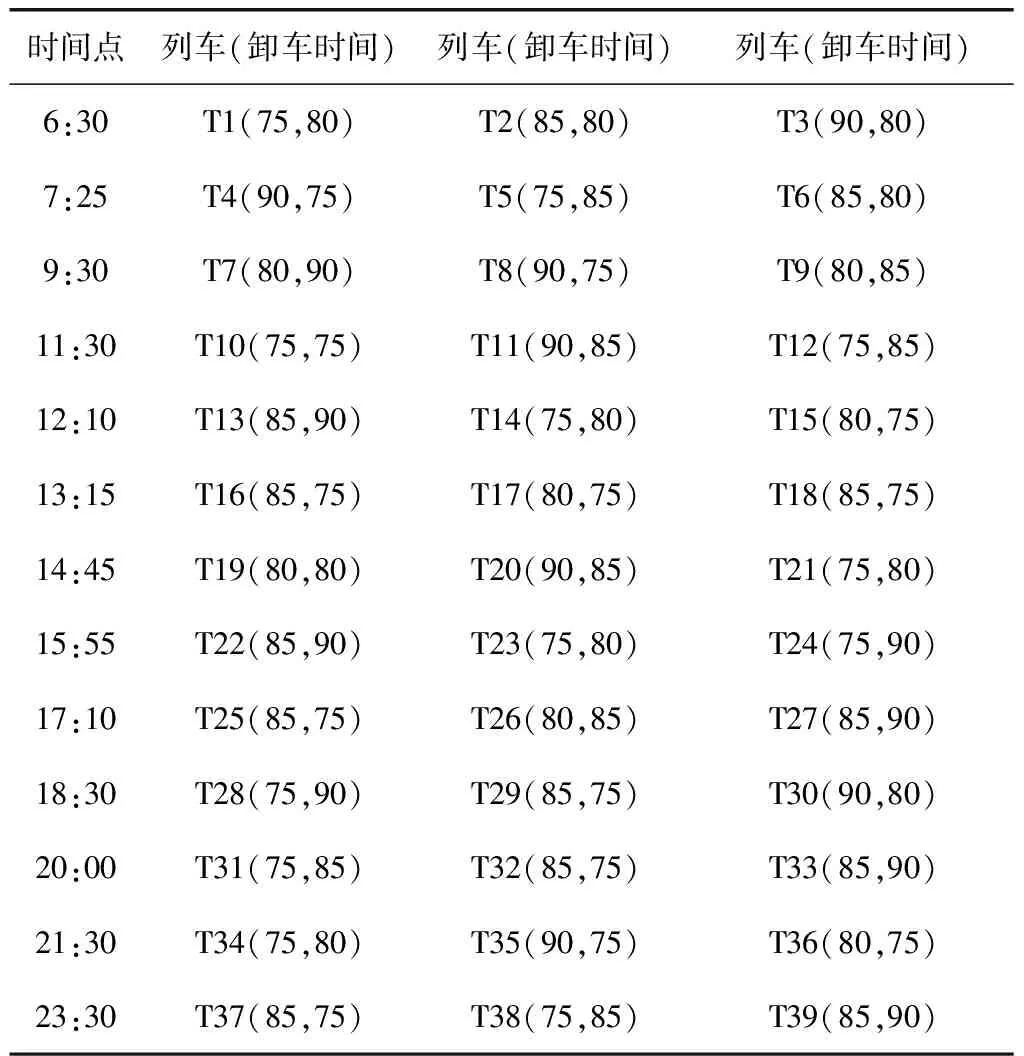
表5 卸车所需时间Table 5 Time required for unloading min

设置ACSSA算法的参数：种群规模n为30, 最大迭代次数Tmax为100，粒子空间维数D为20°。经优化的卸车调度方案甘特图如图11，其中横轴表示列车翻卸时间，纵轴表示4台作业翻车机。

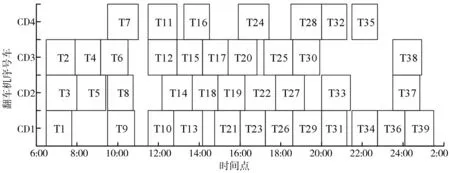
图11 最优调度甘特图Fig. 11 Optimal scheduling Gantt chart

由图11并结合表4和表5的数据分析可知，人为规划的列车调度方案使得列车总在港时间超过80多个小时，而采用优化算法解得的最优列车调度方案，列车总在港时间降低为62.250 3 h，大幅度提高了港口的卸车工作效率，节约了资源和人力消耗。ACSSA算法与ASSA和SSA比较，优化的调度结果相同，但是ACSSA算法只用100次迭代就得到了结果，而ASSA需要300次迭代，SSA需要500次迭代，可见ACSSA算法的收敛速度最快。

6 结 语

以港口的卸车作业为研究对象，以载煤列车在港滞留总时间最短为研究目标，构建了考虑多煤种、火车调度时间、工作机械可用性、作业流程可达性及其相互约束关系等因素的卸车作业模型。提出一种改进樽海鞘优化算法，引入自适应惯性权重，有利于提高算法收敛速度；引入随机柯西变异策略，有利于提高算法寻优能力。5个标准测试函数的寻优结果表明：ACSSA相比于PSO，WOA，SSA，ASSA算法寻优精度更高，收敛速度更快。采用改进樽海鞘优化算法对翻卸工序进行优化，使火车在港滞留时间得到很大的缩减，且算法运算速度快，能满足实际生产调度中的动态性要求，可使港口资源得到充分利用，大大提升港口的运行效率。