基于应用题的小学生画图能力的培养

朱忠立

【摘要】：应用题是小学数学中的重要教学内容，在教学活动中，常出现 “学生怕学，教师怕教”的现象。苏霍姆林斯基认为把应用题“画出来”，其用意在于保证学生有具体思维向抽象思维的过渡。画图法作为解决应用题的一种基本辅助方法，引导学生把抽象的数量关系用线段图画出来能开拓学生思路，帮助他们找到解题的途径和方法。因此，小学阶段培养学生画图和识图的能力非常重要。

【关键词】：画图法;小学数学;解题方法

应用题是小学数学的一个重要组成部分，纵观小学数学教材，从低年级的实物图、圆片、小棒到中高年级的线段图，示意图，画图的思想一直渗透在整个小学阶段的数学教学过程中。可以说，画图作为解决问题的一种基本辅助方法，它能化抽象为直观、化复杂为简单，能够让学生把抽象的数量关系通过画图转化为具体的、形象的表征。因此，教师应该将用画图的方法解决实际问题作为学生解决问题的一种重要的能力来培养。

一、有效转化：培养学生视图能力

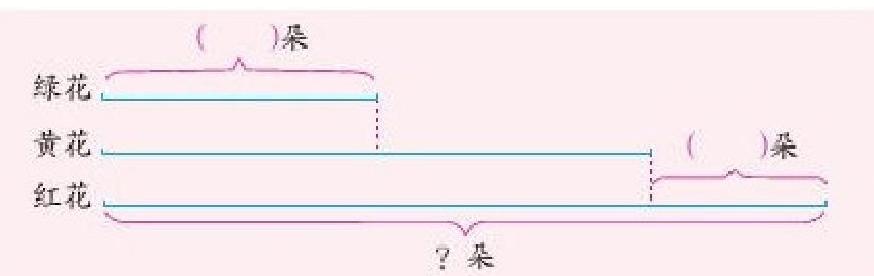
从苏教版的教材我们能够发现，在三年级就已经出现了线段图相关的内容，即三年级上册74页，例2：绿花有12朵，黄花的朵数是绿花的2倍，红花比黄花多7朵。问红花有多少朵？

教学时要引导学生认知3条线段分别表示什么？说一说线段图是怎样表示题中的条件和问题的？要让学生学会看图，能通过线段的长短分析对象之间的关系。接下来的学习中，通过做练习，坚持用线段图分析题目，学生就能有很强的视图能力。同时，也要培养学生将文字表征转换为图形表征的能力，促进学生画图能力的形成。

二、掌握方法：培养学生画图能力

在学生有了一定的视图能力后，下一步就是要培养学生把题目中的信息用图表示出来的能力。首先要鼓励学生尝试画图，低年级的学生对图的理解还停留在单个个体的认知水平，例如会用一个个小棒（竖线）来表示具体的对象，这是最早的抽象的数学符号，这时教师就要鼓励学生常见的几何图形（如：圆圈）来代替，然后用长方形条状，最终演变成用线段代替（如图示）。要引导学生比较这几种画图方法，感受到用线段图更加简洁明了。

然后要让学生都用画图的方式表示题中的条件和问题，用图说明解题思路，初步培养学生的画图能力，通过老师课上的讲解和课后的练习，最终，学生有在头脑中行进画图分析的能力。

在整个培养画图能力的过程中，教师的示范尤为重要。教师要在平时的课堂上、习题讲解时，坚持示范画图，一是让学生感受从繁琐的文字转化为数学图形的简洁，二是让学生时刻处在这样的认知中，体会到画图的重要性。

三、寻找关系：培养学生运用的能力

掌握了画图的方法，最终的目的是为了解题。利用画图解决实际问题，除了让学生借助直观的示意图将题目中的条件和问题以更加直观形象的方式呈现，更加重要的是让学生在实际的解题中，灵活应用画图的方法解决问题。

教材中的应用题，有一些是部分与整体的关系，表示部分是总数的几分之几或者几个部分合起来是一个整体（单位“1”），画图时，一般只要画一条线段表示它们之间的关系;另一种是两个量之间比较，表示A比B多（少）多少，或者A是B的几倍（几分之几），一般要画两条线段表示它们之间的关系。究竟选择哪一种，取决于对题意的理解。

1. 利用线段图解决两个量之间比较的题型

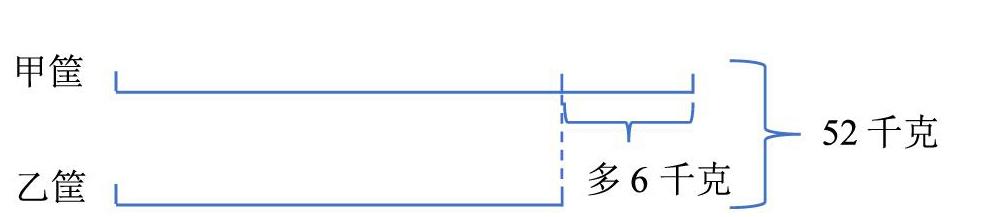
例1，有甲、乙两筐苹果共52千克，甲筐中的苹果比乙筐中的苹果重6千克，求两筐原有苹果各多少千克？

这是一道很典型的A比B多的两个量之间的比较，通过分析画图可以得到下图：

从图中可以很直观地看到甲、乙两筐的数量关系，可以先去掉多的6千克，或者给乙添加6千克，使甲、乙两筐的重量相等，从而计算出结果：

乙筐：（52-6）÷2=23（千克），甲筐：23+6=29（千克）

或者，甲筐：（52+6）÷2=29（千克），甲筐：29-6=23（千克）

2. 利用线段图解决部分与整体关系的题型

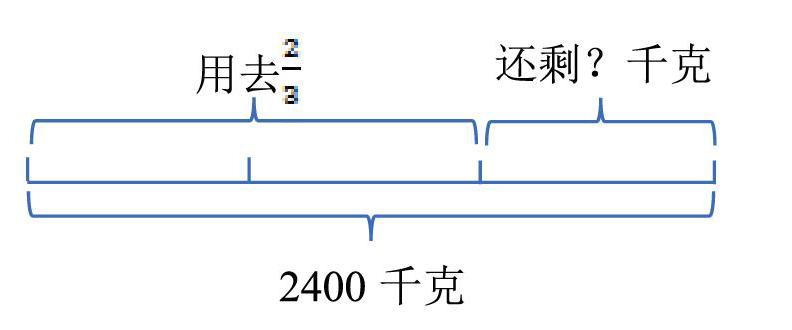
例2，食堂有大米2400千克，用去，还剩多少千克？

审题时，首先要明确2400千克是大米的总重量，用去的和剩下的都是总重量的一部分，通常只需要用一条线段来表示，然后在线段上画出部分和总量之间的关系：

画出图形后，即便是没有学过分数乘法也一样能得出计算结果：2400÷3×1=800（千克）。

3.利用矩形图示法解决问题

在实际的解题中，除了用画线段图的方法，也可以用矩形图表示题目的条件和问题，来帮助我们解题。可以用矩形的长表示一种量，用宽表示另一种量，面积表示这两种量的积。这样可以把抽象的数量关系变得具体形象，便于分析题目。

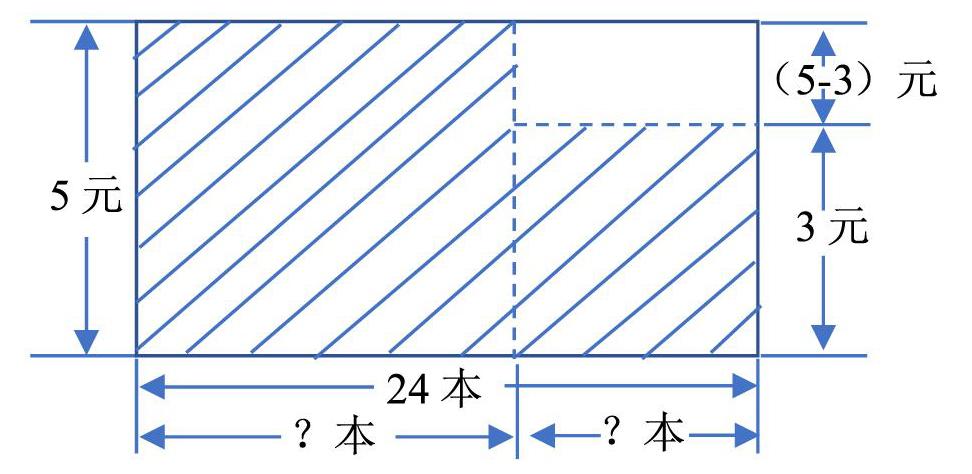
例3，学校采购奖品，李老师买回来5元一本的和3元一本的笔记本共24本，共用去90元。求李老师买回来的两种笔记本各多少本？

这题画线段图是很难表示出题目中的条件和问题，但可以用画矩形图的方法把题目表示正确。

画出来的矩形的长作为总的本书共24本，宽作为比较贵的笔记本的单价每本5元，把实际用去的总的钱90元用阴影描述。通过观察分析。我们知道整个大矩形的面積就是全部都买的5元的总的钱，而阴影部分的面积是实际用去的钱，所以可以得到空白部分的面积表示的是实际用去的钱与都买5元的笔记本花的总钱数的差。利用这个总钱数的差和每本笔记本单价的差，就可以求出3元一本的笔记本的本数，这样整个题目可以得出结果了。

24×5-90=30（元），3元一本的：30÷（5-3）=15（本），5元一本的：24-15=9（本）

所以，画图的方法有很多种，教师要让学生学会画图的同时，要能够灵活应用画图的方法解决问题。

四、巩固提升，培养能力

学生掌握了画图的方法后，教师要对学生的能力进一步的提升，形成技能和技巧。常用的方式有：

1.画图计算。让学生模仿例题和练习题自己画图并列式计算。

2.看图编题。让学生自己根据线段图，编写一个应用题并列式解答。

3.看算式编题、画图。例如老师给学生出示一个2步的四则混合运算算式，让学生自己分析，编一道应用题，并用画图的方法表示出来。

总之，画图作为解决问题中的一种有效的辅助方法，贯穿了小学整个解决问题的教学，要重视图像和画图方法教学的培养。在发现问题和提出问题的基础上，要让学生先说说自己从图中看到了什么，再到解题，感受画图能清楚地理解题意，提高学生解决问题的能力。能力的培养不是一朝一夕的事，需要通过练习不断地训练和强化。

【参考文献】：

[1]王莹.“画图”解决小学数学应用题的对策研究[J].华夏教师，2015（03）：78.

[2]徐向阳.巧画“图”解答应用题[J].课程教育研究，2013（09）：102-103.

[3]金淑芹.教会学生把应用题的题意“画”出来[J].中国校外教育，2010（15）：39+42.

[4]陈玉贤.教会学生把应用题的题意“画”出来[J].教书育人，2009（S3）：73-74.

[5]黄文选.刘梦湘.小学数学应用题解题思路训练[M].北京：北京师范大学出版社，1990：166-167.

[6]高建国.王舍.小学数学教学研究新探索[M].广州：暨南大学出版社，1999：129-132