借助信息技术 提高运算能力

冯维

笔算“两位数乘两位数”属于数与代数课程领域。之前学生已经学习口算乘法与笔算多位数乘一位数，有了一定的知识基础及学习经验，之后，学生还将学习笔算三位数乘两位数。而两位数乘两位数的笔算乘法是由实际问题引出“14×12=？”的计算问题，主要使学生初步掌握两位数乘两位数乘法的计算顺序，教材着重引导学生用两种解决问题的方法，体现解决问题方法多样化。同时，也让学生感受“转化”这一数学思想与方法。教材是由小精灵提出问题，要求用点子图表示计算方法。运用直观的“点子图”作为研究素材，将学生的思考从无意识地分一分、算一算，引导为有意识地思考。满足学生自主探究“算法多样化”的需求，又引导学生对不同方法的比较，从中筛选出与竖式计算相匹配的方法。同时借助现代信息技术，帮助学生理解两位数乘两位数的计算的过程和方法。让学生在理解算理基础上掌握算法，并明确竖式中每一步计算结果的含义，还通过引导学生交流互动，逐步归纳出计算法则。让学生经历计算法则的获得过程，渗透数学思想与方法。

一、借助新型微课，引领学生尝试计算，学习新知

微课是以视频为主要载体，记录教师在课堂教学过程中，围绕某个知识点或教学环节而开展的精彩教与导的全过程。借助微课，主要是答疑解惑，为学生学习新知、掌握基本的数学知识扫清障碍。在学生预习时，就将他们错误的想法消灭于萌芽状态，并借助微课进行尝试计算。

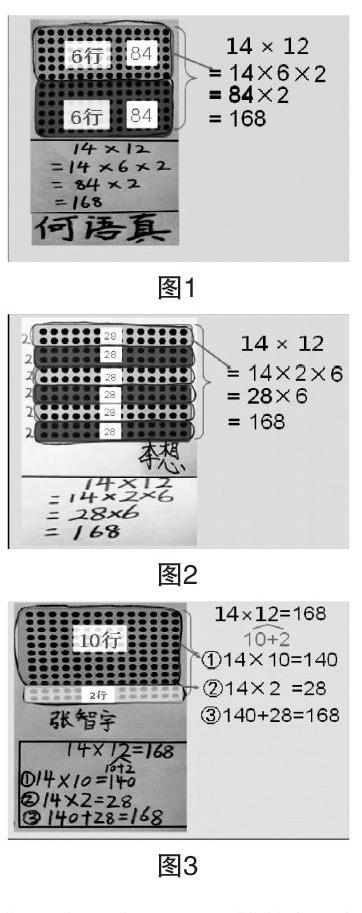
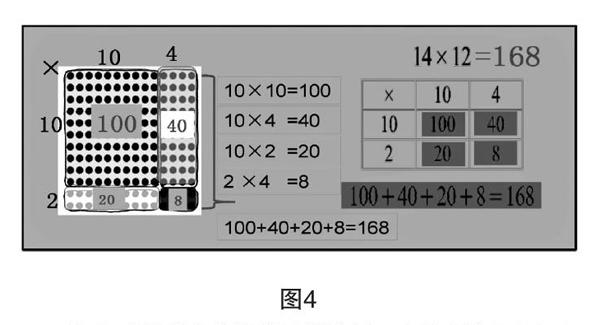
如，教学“两位数乘两位数的笔算乘法”一课时，首先把微课和导学提纲上传到教学助手平台，让学生在课外下载自学，并完成导学提纲上的几道练习，再进行上传，教师可以根据学生的答题情况，预设或调整教学方案。而本节课的重点就是看学生是否理解与正确运用点子图来理解算理，在点子图上“圈一圈”，目的是把点子图划分成若干个较小的点子图直观模型使未知转化成已知，以便分步计算，再累计结果。所以，教学时，教师可以在教学助手中精准展示学生作品（如图1、图2、图3），先让做对的学生亲自上台讲解，说清计算的过程，这时教师又可以借助提前做好的课件直观演示这位学生的计算过程，其实借助直观的点子图呈现算式的形成过程就是算理的形成过程，而有了现代信息技术的支持，就能够把图形到算式、从算理到算法的形成过程清晰地展示给学生，从而，算理的形成过程就会铭刻于学生们的心中。

在解決“12套书一共买了多少本？”这个问题时，让学生结合点子图通过自己圈一圈、画一画等方法，明确“14×12”计算思路。由于学生的知识背景与生活经验的不同，学生出现了不同的算法：把12套分成10套与2套、分成6套与6套、分成6个2套等，在体现了多样化的策略和个性化学习方式的同时，巧妙渗透数形结合思想与转化思想。再借助数形结合，引导学生比较“这3种方法有什么相同点？为什么要先把12拆分？”，为转化思想的渗透建立了直观模型，提高了解决问题的能力。

二、借助信息技术，促使图与表的结合，理解新知

三年级下册的两位数乘两位数的笔算乘法运用了点子图与表格法，而点子图与表格法之间的沟通需要借助图与表之间的直观演示，才能让学生更清晰地明白它们之间的联系。为此，借助信息技术，可以把这一环节制作成微视频方式在课堂上播放给学生观看，直观地演示它们之间的联系（如图4），使学生更深度地理解图表之间的关系，并能很好地沟通和转化两种算法，能够在点子图中找到表格法中数据的原型，在表格中找到点子图中的数据所在，实现了“表中有图，图中有表，图表一家”的理念。

然后，引导学生将笔算过程的每一步算式的含义与点子图联系起来，找出相应的点子图部分（如图5），沟通竖式与拆分计算方法的联系，从而理解竖式计算的算法;依托点子图这个直观模型的操作活动，让学生经历竖式的形成过程，从而清晰理解竖式计算的算理，也能很好掌握计算的方法。

这样，让学生充分体验由抽象算理到直观算法的演变过程，从而达到对算理的深层理解，促进学生对算法的牢固掌握。从而让学生经历运算形成过程中，去构建计算法则。

三、借助信息技术，促进学生互动交流，掌握新知

课中交流互动反馈环节，利用课堂练习对比功能可以再次巩固并提高讲评的效率，提升讲评的品质〔如图6、图7（错例）〕。现场拍照和现场摄像功能是教师的第二大法宝，教师可以现场拍照上传学生的练习，第一时间收集和捕捉最有用的信息进行反馈，让学生在辩错、纠错中巩固新知。教学助手中互动课堂的随机抽人功能，体现了教学的公平性;小组评比功能激发了学生的学习积极性。

最后，教师提出拓展延伸的问题让学生带回去解决，让学生做完后再次提交，教师通过平台了解学生的完成情况，了解学生对所学新知的掌握情况。