2020年中考数学文化试题的赏析与探讨

宋雯雯

【摘要】从古至今，数学从来都不是脱离社会文化发展而孤立存在的.我们要让学生在数学学习的过程中感受文化熏陶，形成数学核心素养，体会数学与文化的融合.《义务教育课程标准（2011年版）》中明确指出：“数学文化作为教材的组成部分，应渗透在整套教材之中.教材可以适时地介绍有关背景知识，激发学生学习数学的兴趣，欣赏数学的优美.”由此可见，数学文化发挥着重要的教育作用.近年来，各地中考试题中频繁出现蕴含数学文化的试题.我们选取2020年部分地区中考试题进行研究，发现主要涉及数学文化与数学思想方法、中国古代数学名著中的问题、数学文化与数学游戏、数学文化与社会生活四个方面.现就部分数学文化试题进行赏析.

【关键词】数学文化;教育;试题

1 试题分析

1.1 数学文化与数学思想方法

赏析 《孙子算经》是我国古代重要的数学著作.传本的《孙子算经》共有三卷：上卷讨论了算筹记数的制度和筹算乘除法;中卷叙述了筹算分数算法和筹算开平方法，以及面积、体积、等比数列等计算题;下卷包含了各种应用问题，如“物不知数”问题即为“大衍求一术”的起源，被称作“中国余数定理”或“孙子定理”.本题以《孙子算经》中绳长问题为背景，考查学生对二元一次方程组的理解，其不仅是建构方程模型的良好素材，还能很好地渗透数学史中的数学思想.

例3 （2020年宁夏银川卷第12题）我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小.用锯去锯这木材，锯口深ED=1寸，锯道长AB=1尺（1尺=10寸）.这根圆形木材的直径是寸.

赏析 本题考查垂径定理结合勾股定理计算半径长度，在与圆相关的题目中如果要求弦长或半径、直径，则需从题目中寻找是否有满足垂径定理的条件，然后构造直角三角形，通过勾股定理進行求解.《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著，是《算经十书》中最重要的一部，集合了战国、秦、汉时期的数学成就.全书分为方田、粟米、衰分、少广、商功、均输、盈不足、方程及勾股九章，共收录246个与生活实践相关的数学问题，是一本综合性的历史著作.它的出现标志着中国古代数学形成了完整的体系.以《九章算术》中历史名题作为中考试题，既可让学生领略我国古代的数学成就，也可以增强学生的民族自豪感和认同感.

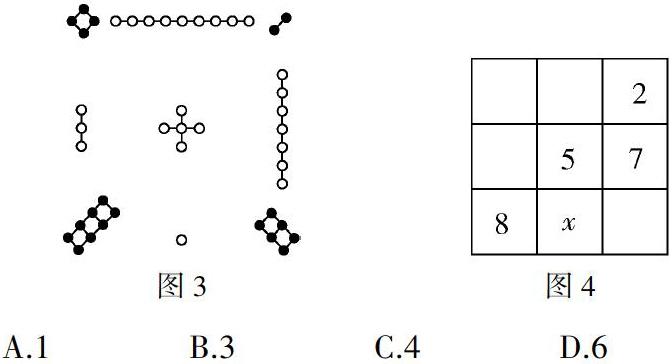
1.3 数学文化与数学游戏

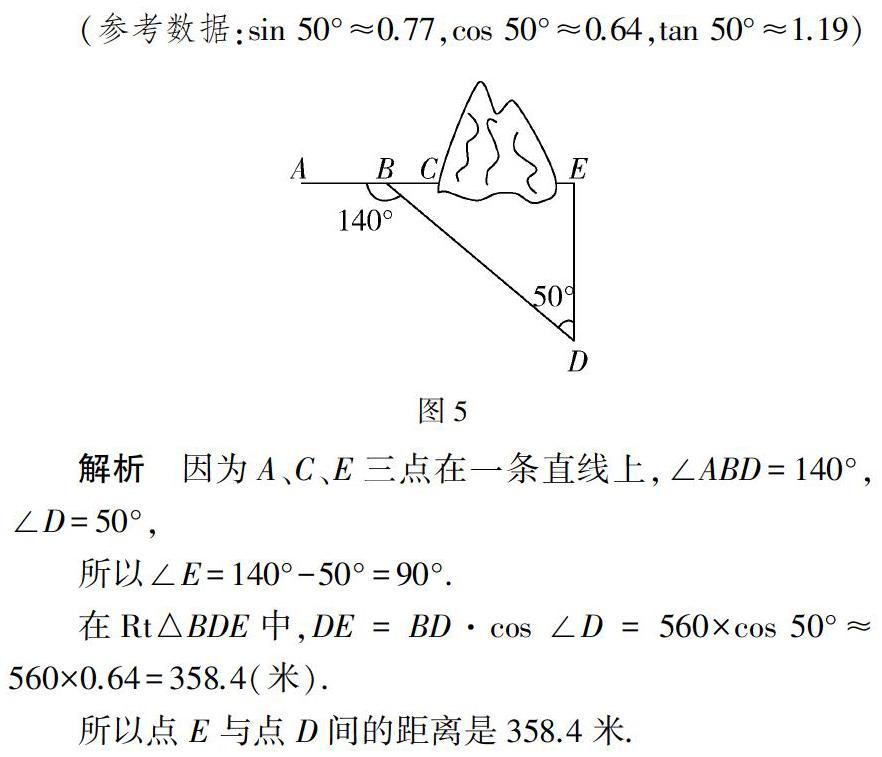
赏析 本题将生活中建立高铁站的问题改编成数学问题，将生活情境抽象为数学模型，考查学生运用三角函数和解直角三角形来解决实际问题的能力，有助于培养学生的数形结合思想、抽象思维以及建构数学模型的意识，同时让学生体会数学的应用价值.

2 反思与建议

数学文化已然成为教育工作者关注的一个焦点，也相应受到中考命题者的青睐.通过对国内部分地区中考数学文化试题的赏析与研究，我们发现数学文化试题类型丰富，在试卷的选择、填空、解答题中均有涉及，且题目难度适中.基于以上研究，本文给出如下几点建议：

第一，数学史的选取要符合学生认知.数学名著中的历史名题多以古文出现，对初中生来说难免晦涩难懂，这就需要给出相应的原文翻译，在避免学生误解的同时，仍可以融入相关数学史内容.但部分试题只是给出数学史背景，且考查方式过于单一，还需进一步提高数学文化与数学知识之间相关度.

第二，生活现实类试题的编制要结合时代特征，增强试题创新性.为避免试题的问题情境老套陈旧，出题人可结合当下社会热点问题来编制试题，所选取的素材不仅要贴近学生的现实，也要体现趣味性和创新性.

第三，改进教学方式，促进数学文化教育途径多样化.教师要根据学情，将数学文化知识有效地融于课堂.例如，可以用观看数学史视频、表演数学小话剧等方式增强学生的参与感，通过发生法使学生置身于历史情境，培养学生探索知识的能力及核心素养.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2]陈慧本.论历史时间的空间化及其与隐喻、叙事的关系[J].史学月刊，2019（04）：111-121.

[3]余小芬，闵蓉，刘成龙.2018年中考数学文化型试题背景赏析[J].数学教学通讯，2019（14）：79-81.