2阶瞬态提取变换在机械故障诊断中的应用

胡志峰，李志农，，毛清华，于 刚，张旭辉

(1.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063；2.西安科技大学 陕西省矿山机电装备智能监测重点实验室，西安 710054；3.济南大学 自动化与电气工程学院，济南 250022)

采煤机摇臂作为采煤机的重要部件，是采煤机直接承担截割煤壁与进行动力传递的关键环节，其运行状态正常与否成为煤炭开采产量高低的关键因素[1－3]。相对于一般行业齿轮箱的运行要求，采煤机摇臂齿轮箱的运行要求较高，摇臂齿轮传动系统既要随着截割煤壁高度的不同而上下调节，又要随着采煤机沿截割煤壁的水平方向移动[4－5]，此外，设备的老化和人停而机不停的生产运行模式以及工作人员非标准化操作等因素，采煤机摇臂齿轮传动系统极易发生故障。因此对采煤机摇臂齿轮传动系统进行有效快速的故障诊断，对煤矿高效及安全生产具有重要意义。而时频分析方法是进行故障诊断最为有效的方法之一，近年来，随着时频技术的不断发展，涌现了大量实用有效的时频分析方法，如短时傅里叶变换、小波变换、广义S 变换、魏格纳威尔变换（Wigner-ville distribution，WVD）等[6-12]，然而，这些时频分析方法由于自身算法的原因，易受到海森堡不确定性原理的限制（如小波变换、短时傅里叶变换），魏格纳威尔变换虽有较高的时频分辨率，但容易产生交叉项。为了获取更高的时频分辨率，许多学者将时频重排方法引入到传统的时频分析中，时频重排方法本质是在传统时频分析的基础上对能量进行二次重排，以改善时频谱的能量聚集性。Auger等[13]基于传统时频分析方法提出了一种后处理重排算法，利用时频相位信息，通过重排算子将发散的时频能量重排到时频脊线上，从而获取高分辨的时频谱，但不支持对信号的重构。Daubechies 等提出了一种同步挤压小波变换方法[14]，该方法仅考虑频率系数上的重排，牺牲一部分能量聚集性，但保证了多分量信号的拆解和重构性能。文献[15]在同步挤压小波变换的基础上，将原有小波变换框架转换为短时傅里叶变换框架，进而提出了同步挤压短时傅里叶变换方法，该方法在信号的低频部分和高频部分具有相同的分辨率。然而，同步挤压变换仅适用于分析瞬时频率较为恒定的谐波信号，当瞬时频率变化剧烈时，该方法的时频分辨率较为不佳。文献[16]在同步挤压变换算法的启发下，提出了同步提取变换（Synchroextracting transform，SET）方法，该方法是在短时傅里叶变换的基础上，构建出同步提取算子，提取出原始时频谱的时频脊线位置处的时频系数，从而显著提高了时频分析精度。最近，文献[17]提出了基于瞬态提取变换(Transient-extracting Transform，TET)的时频分析方法，该方法能够有效地表征和提取故障信号中的瞬态分量,且具有更高的时频精度。但由于上述方法是建立在1阶信号模态的基础上，故不能较好处理更为复杂的实际信号，为此，在文献[17]的基础上，一种高分辨的时频分析方法—2 阶瞬态提取变换(Second-order transientextracting transform，STET)[18]被提出，该方法能够分析更为复杂的信号，且具有更高的时频分辨率，能够有效克服传统时频分析方法能量发散、特征模糊的问题。因此，基于STET的独特优势，本文将该方法应用到采煤机摇臂传动系统的故障诊断中，并进行仿真和实验验证，能为有效表征出采煤机摇臂传动系统齿轮的瞬态故障特征提供一种有效的方法。

1 2阶瞬态提取变换原理

瞬态提取变换是一种短时傅里叶变换的后处理方法，首先考虑分析冲击信号z(t)=Aδ(t-t0)，通过短时傅立叶变换将其由一维的时间信号变为二维的时频信号：

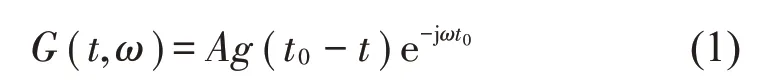
式中：，g(u-t)=e-(2σ)-1t2，通常为高斯窗函数。

由于||e-jωt0=1，狄拉克delta 函数的短时傅里叶变换的能量分布可表示为：

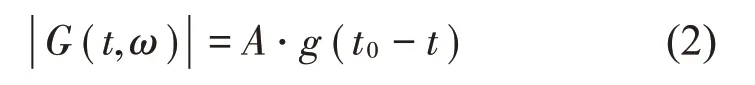
由于窗函数在时间上是紧凑的，其短时傅里叶变换的能量在时间t=t0达到最大值。狄拉克delta函数的短时傅里叶变换会导致群延迟的存在，为精确估计每个狄拉克函数的群延迟，首先计算其短时傅里叶变换的频率的导数，其计算式如下：

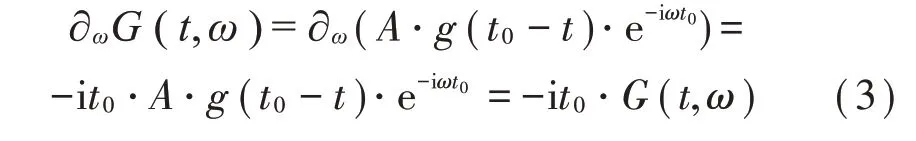
对于任意的(t,ω)，使得G(t,ω)≠0，二维的t0(t,ω)群延时可以计算为：

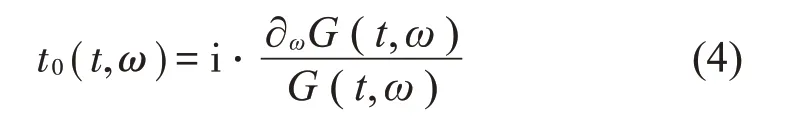
为了去除混叠的时频系数，只保留在时间t0上的时频系数，瞬态提取算子（Transient-extracting Operator，TEO）被提出：

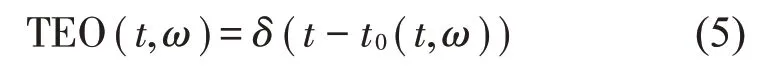
其中：

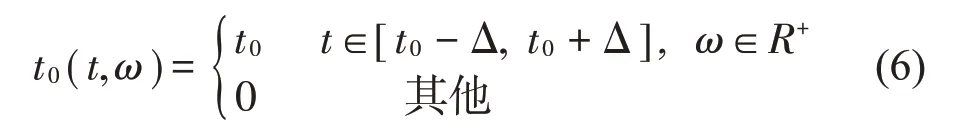
式中：Δ表示窗函数的时间支撑范围。于是，瞬态提取变换可以表示为：

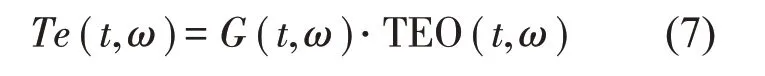
由于狄拉克δ(x)函数有以下性质：

因此上述瞬态提取变换可以表示为：

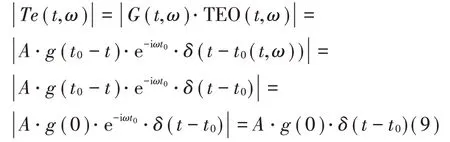
但由于瞬态提取变换本身算法限制，该方法在处理2 阶频变信号时，其时频能量聚集性能下降且增加了一个2 阶频率常量，其时频结果更为模糊[17]。因此需要构建2阶的瞬态提取变换。为更好分析如下信号：

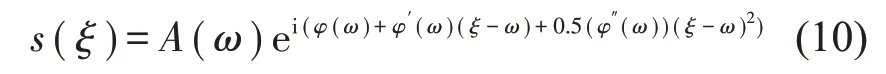
将上述信号进行短时傅里叶变换得到：

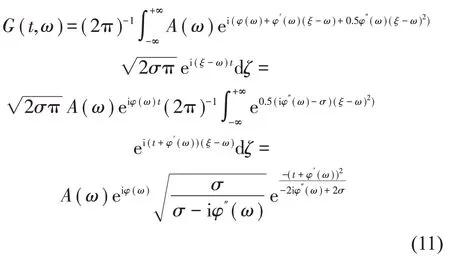
将式（11）代入式（4）得到二维时间群延迟估计：

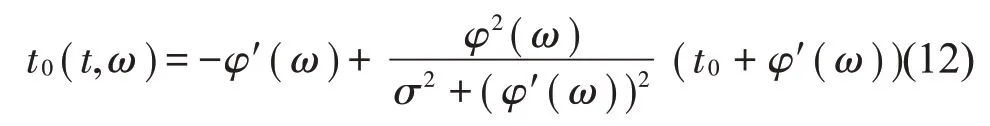
由式（12）推导得到：

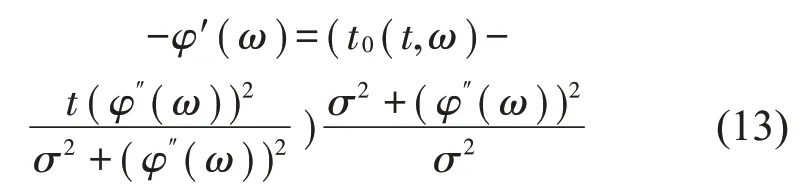
进而有：

从而得到了二维瞬态频率延迟估计。对式（12）和式（14）分别在时间域和频率域求导，得到如下表达式：

受式（13）启发，可以得到以下表达式：

其中：上标[2]表示2阶估计，将式（15）中各表达式代入到式（13）中，则得到：

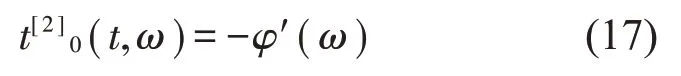
式(17)验证了对于一个2阶频变信号，其二维的群延迟估计是可以得到的。

但其前提是|∂t ω(t,ω)∂ωt0(t,ω)|≠0，因此，一种基于2阶信号模型的修正二维群延迟估计可以得到如下表达式：

为了精确提取信号短时傅里叶变换结果的幅值，在计算短时傅里叶变换时需采用群延迟脊线t=-φ′(ω)，从而得到：

由式（19）进而可以得到修正的2阶短时傅里叶变换结果：

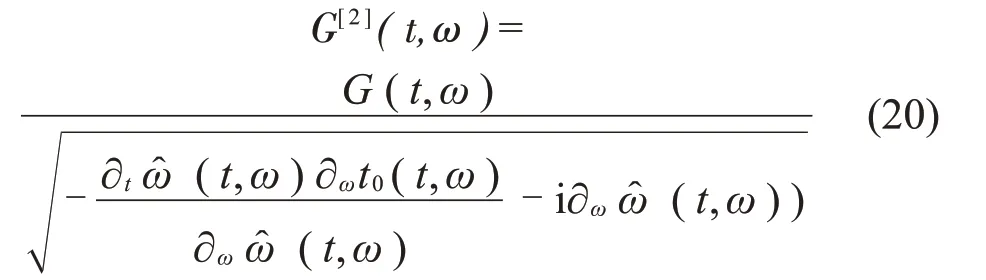
结合式（20）和式（18），可得到计算2 阶频变信号的改进型2阶短时傅里叶变换：

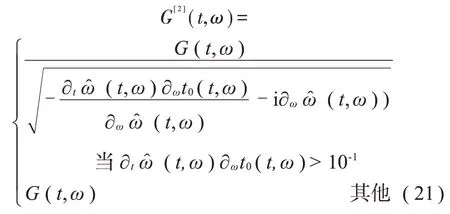
进而可以得到2阶瞬态提取变换表达式：

2 仿真研究

考虑如下调幅调频信号：

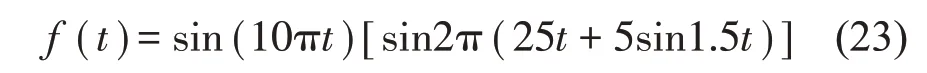
采样频率100 Hz，采样时间为4 s，仿真信号时域图如图1 所示。为验证2 阶瞬态提取变换方法的有效性，将该方法与同步挤压短时傅里叶变换(SST)、同步提取变换（SET）、瞬态提取变换（TET）进行对比分析，对该仿真信号分别进行同步挤压短时傅里叶变换、SET和2阶瞬态提取变换，得到时频分布分别如图2至图5所示。

图1 仿真信号时域图

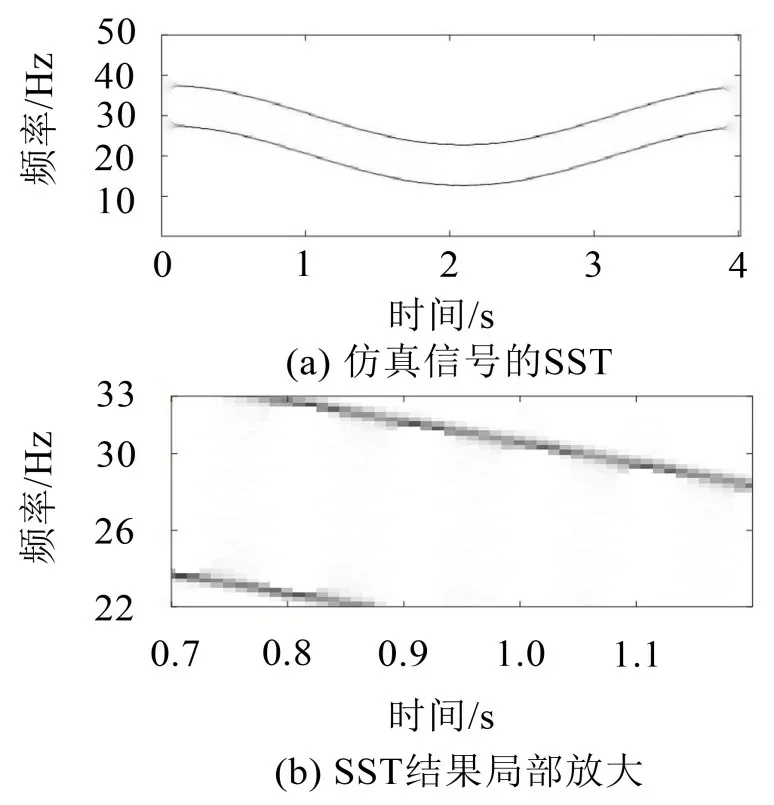
图2 SST方法

对比图2、图3、图4和图5，可以看到STET具有最高的时频分辨精度，在图3中，SET的时频精度虽然高于SST，但其结果存在频率混叠情况，对比图4与图5 可知，与TET 方法相比，STET 方法的时频结果得到了明显改善。

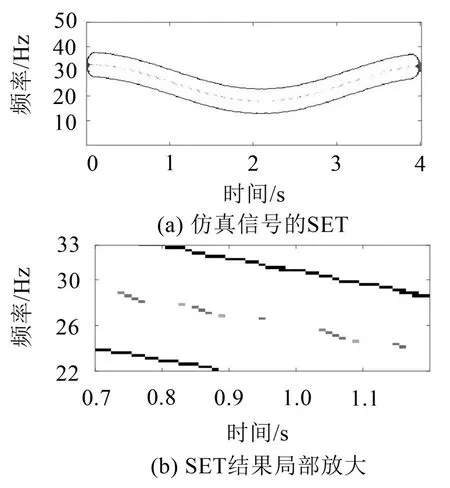
图3 SET方法

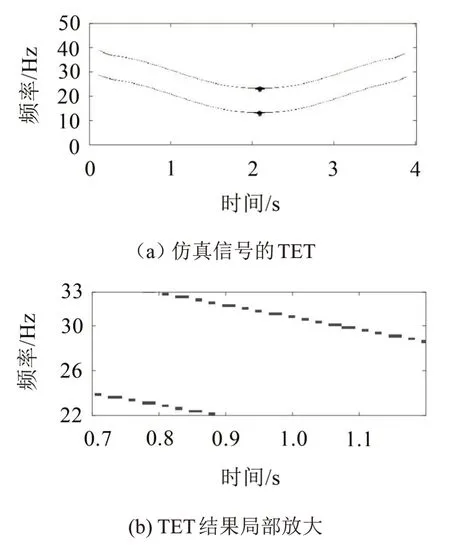
图4 TET方法

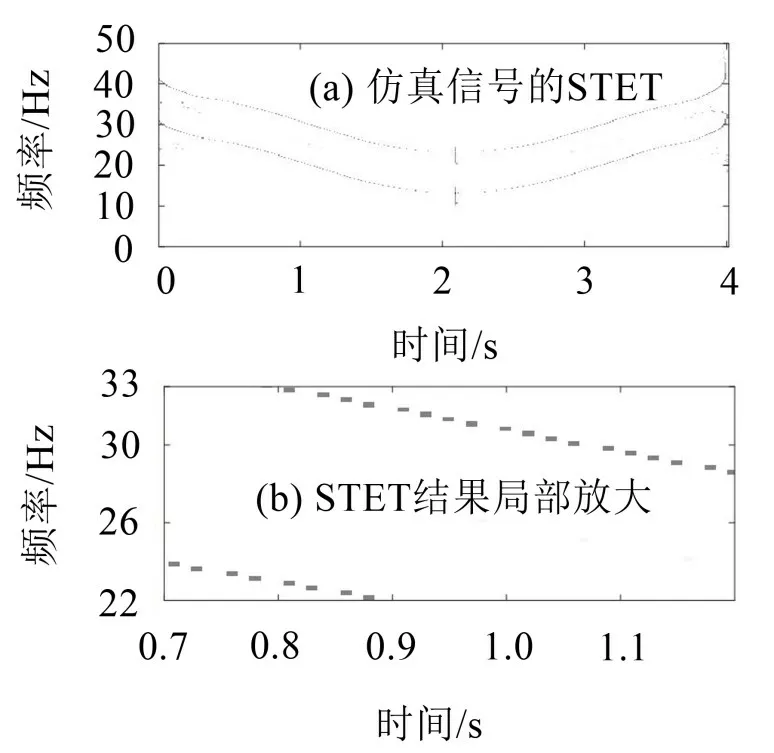
图5 STET方法

为了进一步验证STET的抗干扰性，在上述仿真信号中添加11.08 dB 高斯白噪声，设置相同采样频率和采样时间，图6为加噪的仿真信号时域图。

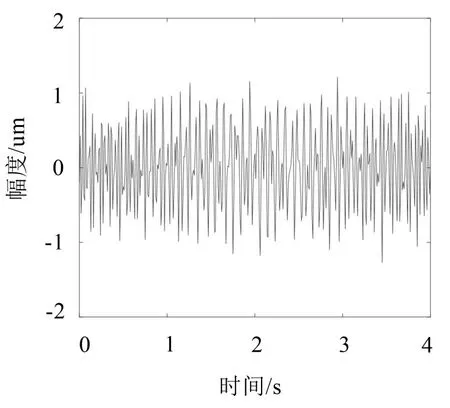
图6 仿真信号时域图(加噪)

将该含噪信号分别采用SST、SET、TET和STET方法进行分析，得到的时频分布分别如图7 至图10所示。由图7 可知，噪声的影响使得SST 的时频结果变得更为模糊，而在图8中，SET的时频结果存在频率混叠情况，且已受到噪声信号的干扰，而对比图9和图10可知，虽然有噪声成分的存在，但TET和STET的时频结果均保持了较高的时频精度，具有一定的抗噪性能，而STET 的时频结果与经TET 处理的结果相比，其时频精度得到了进一步的提高，因此，相比SST、SET、TET方法，STET方法在抗噪性、时频精度等方面具有更为明显的优势。

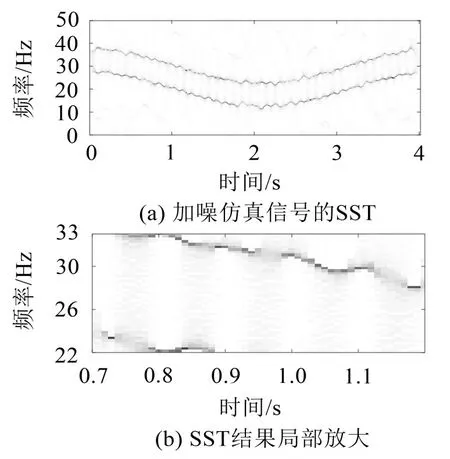
图7 SST方法

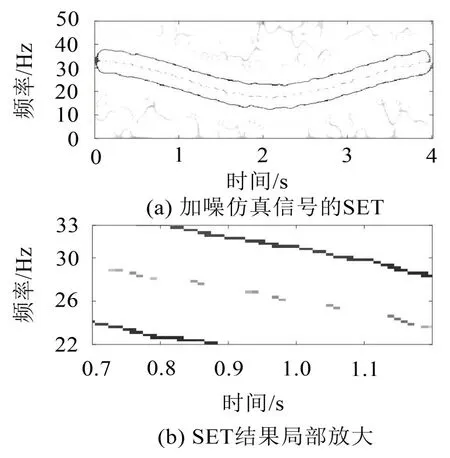
图8 SET方法

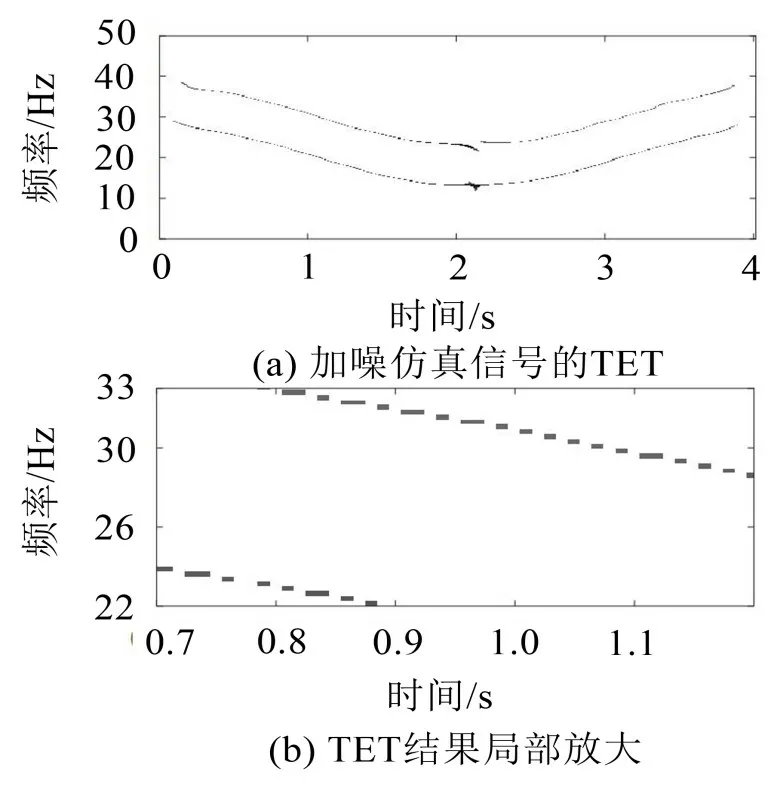
图9 TET方法

图10 STET方法

3 实验研究

为了进一步验证STET 方法的有效性，在此将该方法应用到采煤机摇臂传动系统的故障诊断中。本文采用的数据来源于陕西省西安市煤矿机械有限公司，采煤机型号为MG1480型，利用采煤机工作过程中获得的振动数据进行分析。该型号的采煤机摇臂机构具有左右两侧相互对称结构，右侧驱动配备有破碎机构，左侧摇臂传动系统运行过程中声音偏大。安装配套的振动信号拾取设备进行相关数据采集工作，传感器选取DH186E型ICP内置压电加速度传感器，该传感器有效工作频响范围为0.5 Hz～5 000 Hz，最大测量加速度为500 m/s2，安装谐振频率为25 000 Hz，灵敏度为10 mV/ms2，工作温度范围为-20 ℃～80 ℃。采集卡选用美国虚拟仪器公司生产的NI9375型采集卡，分辨率为24 bit，共有12个同步采集通道，设置的采样频率为51 200 Hz。通过底座磁铁吸附的方式将传感器分别安装在传动轴轴向及径向(1号和2号测点)、惰轮4轴向和径向(3号和4号测点)、滚筒轴向及径向(5 号和6 号测点)等位置处，用于采集摇臂工作过程中内部齿轮传动系统产生的振动信号，摇臂机构传动系统及传感器布设示意图如图11所示。

图11 摇臂机构传动系统及传感器布设示意图

右摇臂故障出现在Z4 齿轮上，对1 通道采集的故障振动信号进行处理，设置采样频率为512 000 Hz，采样点数为2 048，Z4 齿轮的理论啮合频率为472.5 Hz，旋转频率为17.5 Hz，其2 倍频为945 Hz，图12 为试验信号的时域图，图13 至图16 分别为采用上述4种方法处理的时频结果图。

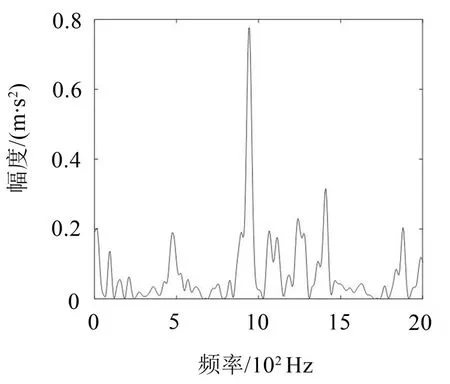
图12 故障信号时域图

图13 SST方法

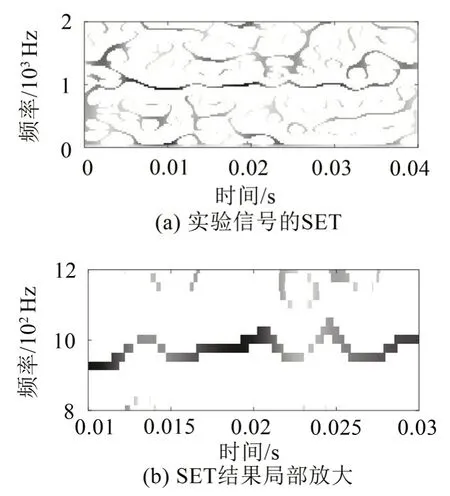
图14 SET方法

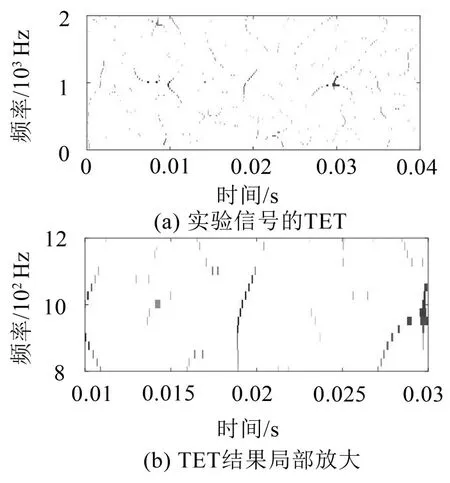
图15 TET方法

图16 STET方法

设置相同的窗函数宽度均为512，故每隔0.01秒对实验信号进行一次时频变换处理，采用上述4 种时频分析方法对采煤机摇臂传动系统的故障信号进行分析。图13（a）是采煤机Z4齿轮振动信号经SST方法得到的时频分布，而图13（b）是图13（a）在时间0.01～0.03秒的局部放大图，由图13（b）可知，在0.02～0.025秒的时间段内，采用SST方法虽然能表征出故障的特征频率，但不可避免将噪声成分“挤压”至故障特征成分中，造成时频结果模糊。而在图14中，由于同步提取变换算法实质是在短时傅里叶变换的基础上，通过同步提取算子在频率域脊线上提取短时傅里叶变换结果，图14(b)反映了频率成分在时间上的变化情况，由于窗函数的影响，加之原有故障信号噪声成分的存在，虽提取出了故障特征频率，但在时间域上不可避免受到了噪声的干扰，所以其时频能量分布在0.02 s～0.025 s的时域内，在时域方向上，呈现出线性变化。而由于瞬态提取变换算法实质是在短时傅里叶变换的基础上，通过瞬态提取算子在时间域脊线上提取短时傅里叶变换结果，故其提取的结果在频率域方向呈现出线性变化。图15是采用TET方法得到的信号时频能量分布图，图15（b）是图15（a）在0.01 s～0.03 s 内频域范围为800 Hz～1 200 Hz 的局部放大图，由图15（b）可知，采用TET 方法提取出了信号的故障频率，能够反映出某一瞬态的频率变化特征情况，即在0.015 s～0.02 s的某一瞬态，提取出故障特征频率二倍频945 Hz，但其时频精度特别是频率方向上的精度有待进一步提高。通过构建2阶瞬态提取算子在TET的基础上构造出STET方法，利用STET方法得到的时频分布如图16 所示。由图16(b)可知，采用STET 不仅表征出了故障特征频率，而且对于故障信号的2 倍故障频率也能够有效识别，进一步提高时频分辨率，能够提取出故障的特征频率。

通过上述分析可知，STET 方法相比SST、SET和TET 具有明显的优势，能够有效地表征采煤机摇臂传动系统故障信号的瞬时时频特性，得到的时频结果能反映故障的频谱特征，由此可见，STET 为采煤机摇臂传动系统的故障诊断提供了一种有效方法。

4 结语

(1)2阶瞬态提取变换是在短时傅里叶变换原理的基础上，引入2阶瞬态提取算子，能够处理更为复杂的多分量信号。本文将该方法引入到采煤机摇臂传动系统的故障诊断中，提出了一种新的故障诊断方法，并进行了仿真和实验验证。

(2)仿真结果表明，与现有同步挤压短时傅里叶变换、同步提取变换和瞬态提取变换相比，该方法不论在时频分辨率上还是在抗噪声方面都具有明显的优势，STET 具有最佳的时频精度，且具有一定的抗噪性能。

(3)最后将该方法应用到采煤机摇臂传动系统的故障信号分析中，该方法能够有效提取出故障频谱特征，时频精度显著高于传统的时频分析方法，能够体现出在瞬态提取故障特征方面的优势。