曲线超高率对跨座式单轨车桥耦合系统振动影响

肖 乾，高雪山, 周新建, 李子珺

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

近年来，跨座式单轨车辆凭借自身占地面积小、有较强的过陡坡及小半径路况转弯能力、污染及噪声小、成本低等优势成为众多城市所青睐的城市轨道交通方式之一[1-2]。跨座式单轨车辆不同于传统钢轮钢轨车辆，转向架上的走行轮、水平轮（包括导向轮和稳定轮）、橡胶充气轮胎组成了其独特的走行机构，车辆跨坐在特制的轨道梁上行驶[3-6]。车辆运行在曲线线路上时会产生离心力，而这种离心力的作用会使车上的旅客因向外倾斜而出现疲惫感以及不舒适感，因此在设计跨座式单轨车辆沿轨道梁运行的曲线线路时，需要在曲线轨道上设置一定的超高，再通过借助车辆重力的水平分力来与离心力相互抵消，达到内外轨道受力均匀，所设置的轨道线路超高率值会直接影响车桥耦合系统的振动，进而影响乘客的乘坐舒适性以及车辆的运行平稳性[7-9]。刘浪等[10-11]根据山地城市单轨交通系统的特点，提出车辆的颠簸强度可以通过降低线路的超高变化率来控制，即可通过其提高车辆运行的平稳性。许亮[12]针对一种新型的单轴转向架跨座式单轨车辆结构建立了“车-轮-轨”耦合动力学模型，探究了不同曲线超高率对车辆动力学曲线通过性能的影响，结果证实曲线超高率确实显著影响了车辆曲线通过性能。文献[13]通过编制VB 语言程序建立单轨动力学模型，研究了速度、载重以及线路曲率半径对跨座式单轨车桥耦合系统动力响应的影响。

综上所述可知，轨道线路的超高率、曲线半径等参数会直接影响到车辆系统的相关动力学性能，现有研究针对曲线超高率对单轨车辆及轨道梁振动的影响深入探究较少，且车桥耦合系统模型往往将轨道梁理想化为刚体，而忽略了其实际上的柔性变形。为此，本文将轨道梁作为柔性体，建立跨座式单轨车桥刚柔耦合模型，详细探究曲线超高率对车桥系统的影响。

1 跨座式单轨车桥耦合系统

1.1 车桥耦合系统振动理论

（1）单轨车辆子系统振动方程

将跨座式单轨车辆视为一个由车体及两个转向架3 部分所组成多刚体系统，忽略各刚体部分较小的纵向振动，考虑横摆、浮沉、侧滚、摇头及点头5个自由度。根据车体及转向架的运动，可推出单轨车辆运动微分方程为[14]：

式中：m、c、k分别代表车体、前转向架和后转向架间的质量、阻尼、刚度，下标c代表车体，下标ff1代表前转向架，下标rf2代表后转向架，q̈、q̇、q分别对应车辆加速度、速度以及位移列向量，等式右侧的Fc、Fff1、Frf2依次代表车体、前转向架和后转向架受到的载荷列向量。

（2）轨道梁子系统振动方程

跨座式单轨车辆走行轮和梁平面接触，导向轮和稳定轮与梁侧面接触，使得整车骑跨在轨道梁上运行，本文研究的单轨车辆所对应轨道梁主要参数如下：梁截面高宽为1 500 mm×800 mm，材料密度为2 650 kg/m3，弹性模量为3.75×1010Pa，泊松比为0.2。基于三维铁木辛柯梁理论，采用有限单元法[15－16]来描述轨道梁。柔性轨道梁振动微分方程如下：

式中：E为轨道梁的弹性模量，A为截面面积，ρ为材料密度，G为剪切模量，Iy为相对Y轴的惯性矩，Iz为相对Z轴的惯性矩，ky为Y平面上的剪切修正因子，kz为Z平面上的剪切修正因子，ys和zs分别为剪切中心距几何中心（重心）的横向及垂向距离，xw(t)为轮胎所处的纵向位置，轮胎作用在轨道梁上的纵向力、横向力及垂向力分别记为Fx(t)、Fy(t)、Fz(t)，u、ψ、θ为轨道梁重心处沿X、Y、Z轴的位移矢量，φ、v、ω为剪切中心处沿X、Y、Z轴的位移矢量。

（3）车桥耦合系统振动方程

根据跨座式单轨交通系统中车辆和轨道梁接触位置的位移一致性及两者相互作用关系，将车辆和轨道梁作为两个子系统，得出车桥耦合振动方程：

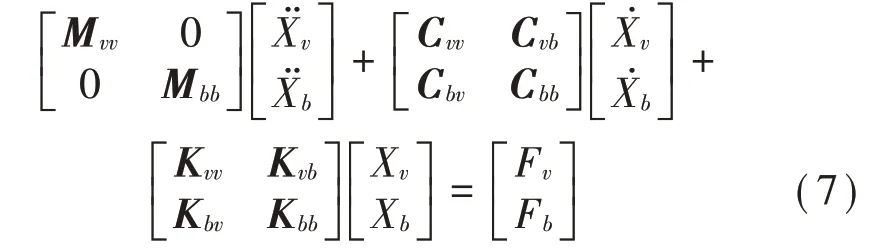
式中，分别用M、C、K表示车辆的质量、刚度和阻尼，下标vv、bb、bv、vb表示对应的车桥相互作用的量̈、、X表示加速度、速度和位移，Fv和Fb代表车辆和轨道梁相互作用时相关的作用力。车辆行驶于轨道梁上，轨道梁产生明显的振动变形，又将振动经由轮胎传递给车体，两者相互作用相互影响。

1.2 单轨车辆系统响应模型

图1所示为某型跨座式单轨车辆的系统输入至响应输出的整个过程，基于多体动力学软件UM 环境，最终建立了一个具有42个自由度的单轨动力学模型，对应该型车辆的主要结构参数如表1 所示。基于参数化建模功能，在后续研究中可实现任意输入量与输出响应的映射关系。下文将对本文研究的主要输入参数和系统输出响应进行介绍。

表1 车辆主要结构参数

图1 某型跨座式单轨车辆仿真模型

（1）曲线超高率

为了平衡车辆过曲线路段时所产生的离心力，通常需要在车辆运行的曲线线路上设置一定的超高率来保证车辆的曲线通过性能[17－18]。GB 50458－2008 跨座式单轨交通设计规范中定义超高率为：曲线段轨道梁绕其中心旋转后角度的反正弦函数值的百分数。曲线超高率示意图如图2所示。

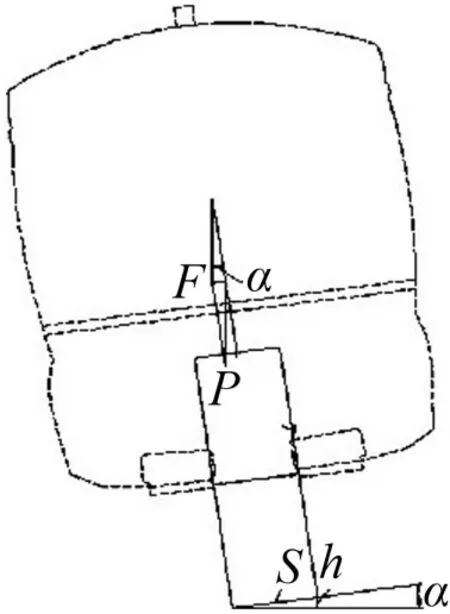
图2 单轨车辆超高示意图

曲线超高率的计算公式为：

式中，轨道梁的旋转角度为α，轨道提升高度为h，S表示轨道梁的宽度，F为向心力，P为单轨车辆的自重。

当车辆过曲线段时，由力学原理可知产生的离心力为：

当重力分量向心力F刚好平衡离心力F离时，车辆曲线运行状态最佳，因此不同工况下对应的最优超高率可由式（10）计算得到：

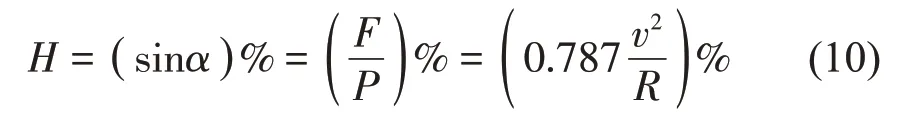
（2）系统响应

基于所建立的单轨车辆-柔性轨道梁动力学模型，相较于刚性梁，考虑不同曲线超高率下的柔性轨道梁特征响应，轨道梁跨中位移表现出车辆经过时车轨耦合作用下的轨道梁产生的形变情况，轨道梁跨中振动加速度则体现了在车辆运行时和外部激励下的轨道梁振动特性；从车辆角度出发，研究水平轮径向刚度、车体侧滚角、车体质心位移量等响应可以有利于判断车辆过曲线时的运行性能（车辆是否发生侧滚）及安全性（是否脱轨），通过监测车体质心振动加速度可以更好判定车辆的运行性能和平稳性。

2 超高率对轨道梁动力响应的影响

结合理论分析与工程实际，取曲线超高率为4%、6%、8%、10%、12%、14%、16%，曲线线路由直线段、缓和曲线段、圆形曲线段、缓和曲线段、直线段组成，具体线路参数如表2 所示。单轨车辆以40 km/h、50 km/h、55 km/h、60 km/h、65 km/h 速度行驶于轨道梁上并以确定性的轨道不平顺样本模拟不平顺激励，对各对应工况下的轨道梁跨中动力响应值进行仿真分析。

表2 轨道模型参数

由图3至图4可发现，在研究范围内当改变曲线线路的超高率时，轨道梁跨中竖向位移总体上先减小后增大；对于40 km/h和50 km/h速度工况，随着超高率的增大，与其理论超高率的差值越来越大，使得相比其他速度工况两者竖向位移的递减斜率更大，当单轨车辆以40 km/h速度行驶在轨道梁上时，横向位移响应值逐渐朝向弯道内侧增大，当速度为50 km/h～65 km/h时，横向位移响应值由弯道外侧向内侧先减小后增大，如对于50 km/h速度工况的变化线图，根据公式计算其最优超高率值约为6.56%，当设置的超高率小于该值时，为欠超高，随着超高率增加逐渐接近该值，振动渐趋于平衡，当设置的超高率大于该值时，为过超高，因此横向位移朝弯道内侧方向增加。

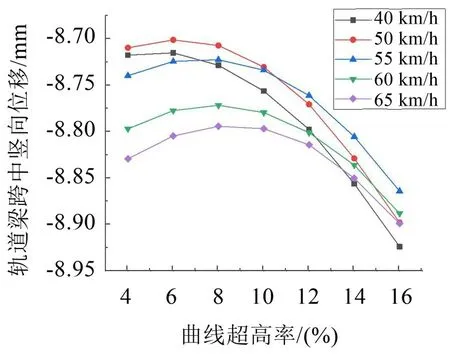
图3 曲线超高率对轨道梁跨中竖向位移的影响

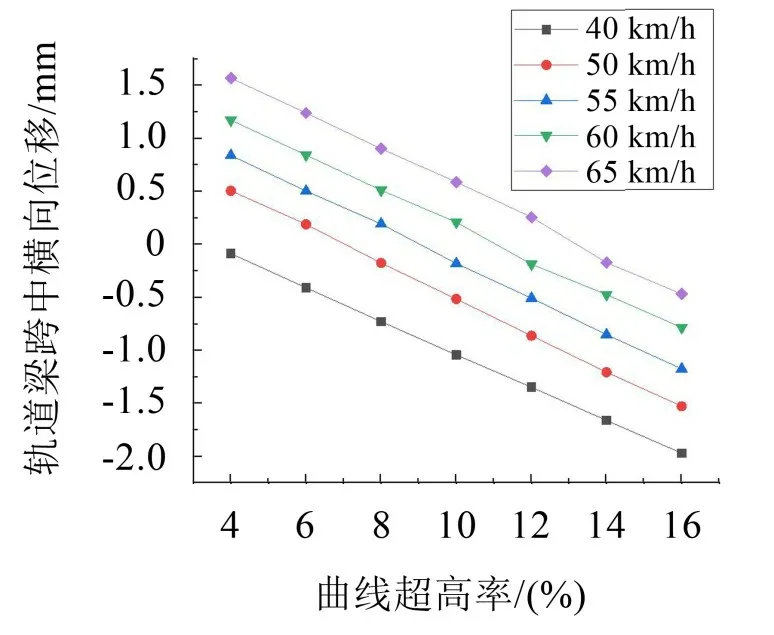
图4 曲线超高率对轨道梁跨中横向位移的影响

3 超高率对车辆动力响应的影响

3.1 超高率对水平轮径向力影响

由图5 至图8 可知，当速度恒定时，曲线超高率越大，导向轮FL的径向力越大，稳定轮FL的径向力越小；若曲线超高率为定值时，车辆行驶速度越快，朝外侧的导向轮径向力减小，朝内侧的导向轮径向力则增大，反之，朝内侧的稳定轮径向力减小，朝外侧的稳定轮径向力增大，这也说明了当行车速度增加时，车体的离心力随之变大，会导致转向架的倾覆力矩变大，内侧导向轮径向力与外侧稳定轮径向力形成抵抗倾覆力矩的抗倾覆力矩也相对应变大。在超高率为10 %的轨道上，车辆的运行速度为60 km/h时，该速度工况下的理论超高率为9.5%，与所设置的超高率较接近，此时轨道超高在较大程度上抵消车体离心力，导向轮和稳定轮径向力的变化幅度较小，若车辆以高于60 km/h 的速度行驶，轨道相比于所设的超高率则为欠超高，朝外侧的稳定轮径向力应该增大从而抵制车辆向弯道外侧倾斜，若车辆以低于60 km/h的速度行驶，轨道相较于所设的超高率为过超高，此时朝内侧的稳定轮径向力应增大来抵制车辆向弯道内侧发生倾斜，对于欠超高和过超高这两种状态，无论是导向轮径向力还是稳定轮径向力的变化幅值都会增大，将导致车辆行驶阻力增大。

图5 不同曲线超高率下的导向轮FL径向力

图6 不同曲线超高率下的导向轮FR径向力

图7 不同曲线超高率下的稳定轮FL径向力

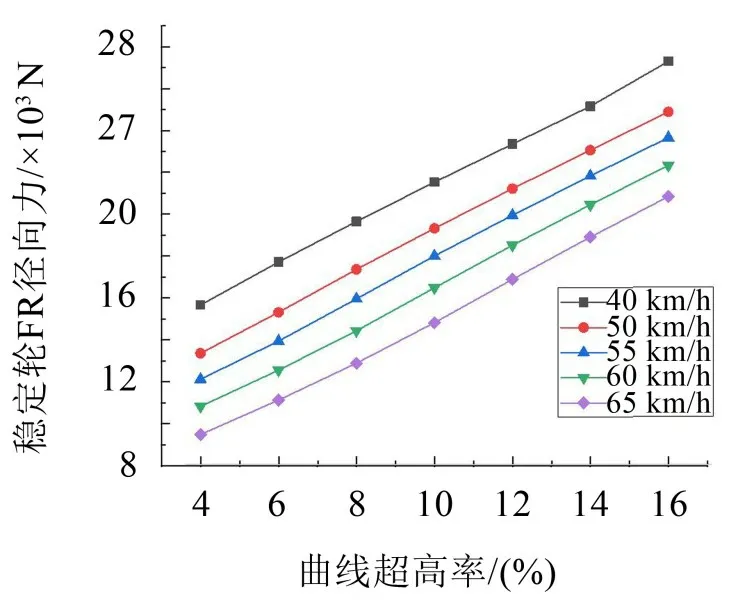
图8 不同曲线超高率下的稳定轮FR径向力

3.2 超高率对车体质心响应影响

图9至图10为不同曲线超高率下车体质心竖向位移响应值、车体质心横向位移响应值的变化曲线。从图中可发现，当曲线超高率增大时，车体质心竖向位移响应值先减小后增大；对于以40 km/h恒定速度行驶的车辆，曲线超高率越大，车体质心横向位移响应值朝着弯道内侧方向逐渐增大，50 km/h～65 km/h速度工况下，横向位移响应值先随曲线超高率增大由弯道外侧向内侧递减，而后位移响应值朝弯道内侧呈递增的变化趋势。综合比较，曲线超高率对于车体质心横向位移响应的影响大于对于竖向位移响应的影响。

图9 曲线超高率对车体质心竖向位移的影响

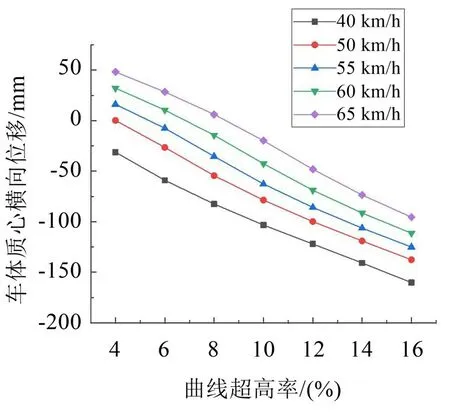
图10 曲线超高率对车体质心横向位移的影响

图11 和图12 为不同曲线超高率下车体质心竖向加速度响应值、车体质心横向加速度响应值的变化曲线。由图观察到，车体质心竖向加速度响应值随曲线超高率的增大而增大，横向加速度响应值先随曲线超高率的增大由弯道内侧朝向外侧减小，后朝弯道外侧方向增大。可发现，车体质心横向加速度响应相比竖向加速度受曲线超高率的影响更大，结合上述车体质心位移的分析可知，曲线超高率的变化对车体质心横向动力响应的影响更加显著。

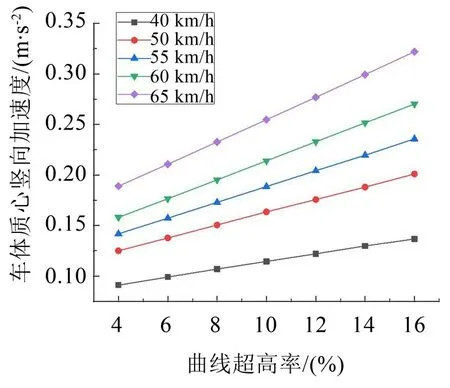
图11 超高率对车体质心竖向加速度响应的影响

图12 超高率对车体质心横向加速度响应的影响

3.3 超高率对车体侧滚角影响

车体侧滚角也是反映车辆曲线通过时安全性以及旅客乘坐舒适感的一个重要指标，图13体现了曲线超高率的改变对车体侧滚角的影响，由图可观察到，当曲线超高率增大时，车体侧滚角从向外侧倾倒逐渐过渡到向内侧倾倒，且随着车辆运行速度的提高，车辆从向内倾倒过渡到向外侧倾倒，这表现出由于车速的增大导致离心力的增大。

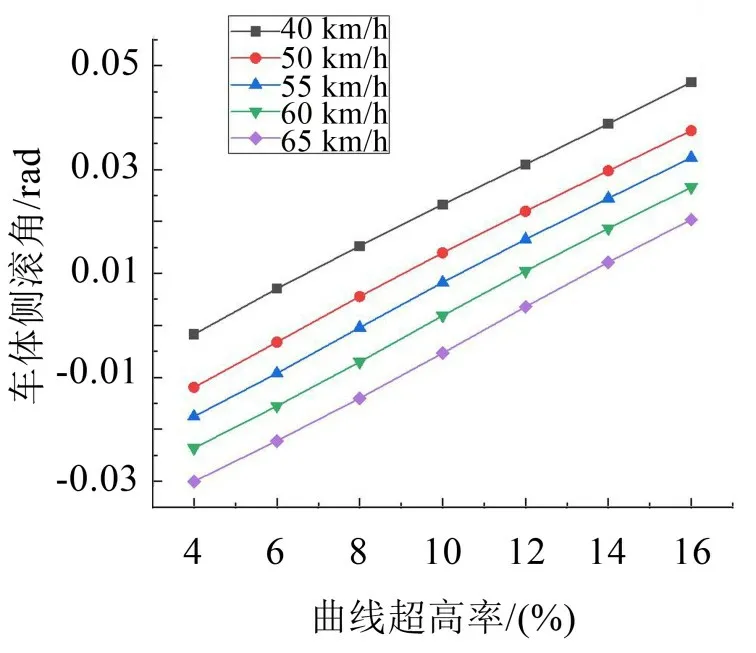
图13 曲线超高率对车体侧滚角的影响

4 结语

（1）曲线超高率增大时，轨道梁跨中竖向位移响应值先减小后增大，车辆以40 km/h速度工况运行时，横向位移响应值逐渐朝向弯道内侧增大；速度高于50 km/h时，横向位移响应值由弯道外侧向内侧先减小后朝内侧增加。轨道梁跨中竖向加速度随曲线超高率有递增的趋势，横向加速度响应值先减小后增大。

（2）曲线超高率对车体质心横向动力响应的影响比对竖向动力响应的影响更加显著，同时对系统横向动力响应的影响大于对竖向动力响应的影响。

（3）定速工况下，曲线超高率越大，朝弯道内侧的导向轮径向力增大，稳定轮径向力减小；曲线超高率为定值时，车辆运行速度越快，车体的离心力随之变大，导致转向架的倾覆力矩变大，此时朝外侧的导向轮径向力减小，朝内侧的导向轮径向力则增大，内侧导向轮径向力与外侧稳定轮径向力形成抵抗倾覆力矩的抗倾覆力矩变大。