基于布设障碍的人流控制方法对人群行走步频的影响研究

何 卫，崔 航，鲁宛杰

(中国地质大学（武汉）工程学院，武汉 430074)

近年来，以大跨度高铁车站、人行桥、体育场馆为代表的大跨度空间结构在我国大量涌现。这类结构自振频率低，阻尼小，在常规的人群荷载（步行1.6 Hz～2.4 Hz、跳跃3.0 Hz、跑步3.0 Hz 左右）[1]作用下结构响应十分显著，其振动舒适度问题较为突出。国内外学者围绕大跨度空间结构的人致振动舒适度与控制问题开展了一系列卓有成效的研究工作，这些工作主要集中在人致荷载模型[1－4]、结构精细化计算模型[5]、结构人致振动分析方法[6-9]、振动控制[10-11]等方面。

振源、传播途径和受振体构成一个完整的振动传播链条。目前国内外围绕大跨度空间结构的振动控制工作主要针对受振体展开，主要的策略有两类：一类是进行结构优化设计[12]，通过改变结构自振频率来避开人行荷载的主频段；另一类是通过施加被动式控制装置（如TMD 等）或（半）主动控制装置[13-15]，将振动能量转移至控制装置，并通过阻尼器耗散能量，以达到控制振动目的。事实上，从振源入手，通过减小荷载以降低结构响应，在风工程等领域已有较多的应用实例[16-18]。如超高层建筑往往需要进行结构外形优化以减小风荷载[16]；大跨度桥梁结构通过结构或断面优化、设置导流板等方式，减小结构风荷载所产生的效应[17]；飞机、高速列车等通过优化车辆外形，以减小气动效应[18]。

障碍布设是交通工程领域进行人流诱导的重要手段。与被动式或（半）主动式减振装置相比，采用障碍布设法进行人流控制具有方便灵活、障碍易于安装和拆卸、成本低和对主体结构影响小等优点。目前国内外运用人流控制手段从减小振源入手来进行结构减振的研究还鲜有报道。本文从振源入手，提出Bottle Neck（BN）和Lane Separation（LS）两种障碍布设方案，通过人为干预人群的运动行为，以降低人群的行走步频及同频比率，达到减小结构的人致振动响应的目的。基于数值模拟手段，系统研究了障碍布设方法及障碍参数对人群行走步频的影响，探索从振源入手进行结构减振的可行性并给出具体的障碍布设建议。

1 基本理论与方法

1.1 人群运动行为模拟

人群的运动既表现出个体之间的自主性、随机性，又具有一定的规律性。为了描述人群的运动，国内外已发展出许多数学模型，它们主要分为宏观和微观模型两类。宏观模型忽略了个体之间的差异，具有代表性的有流体模型、势能场模型等。微观模型考虑了行人个体之间的相互作用和差异性，目前应用较多的主要有社会力模型、元胞自动机模型、格子气模型、多智能体模型等。本文主要采用社会力模型来进行人群的运动行为模拟。

社会力模型中将行人考虑为质点，假定该质点满足牛顿第二定律。模型中考虑了行人到达期望位置的自驱力，行人之间、行人与障碍（边界）之间的排斥力（摩擦力）。考虑N个行人组成的人群，其中第i个人的平衡方程可用式（1）表示[19-20]：式中：下标i表示行人编号；mi表示行人的质量；v0i和e0i分别表示其理想速度和行进方向；vi表示其实际步行速度；τi表示由理想速度v0i变化至实际速度vi的反应时间。

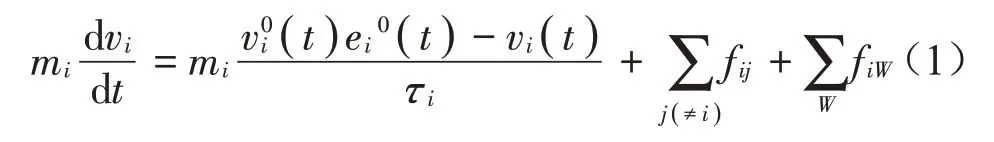
式（1）中方程右侧第一项表示由目标所牵引的自驱力，第二项表示行人i与其他人j（≠i）之间的相互作用力（排斥力），第三项表示行人i与边界（Wall）之间的排斥力。

1.2 基于障碍布设进行结构减振的基本原理

“瓶颈式”（Bottle Neck，BN）（如图1（a）所示）和“分道式”（Lane Separation，LS）障碍（如图1（b）所示）是交通工程领域两种常用的人流诱导方法。本文研究这两种障碍布设方法对人群正常行走特征的影响。BN 法通过减小过流断面的宽度造成局部阻塞，进而影响人群的整体行走速度；LS 式方法主要通过人为诱导人群流向以改变人群行走节奏。这两种方式旨在干扰人群的正常行走方式，从而减小人群的平均步频，并降低人群的同频率。通过有效布设障碍，可大大降低人群荷载与结构的共振概率，从而有效降低结构响应。

图1 障碍布设方式

2 计算参数

2.1 结构模型

结构模型采用如图2所示人行桥结构。其长度L=100 m，宽度D=3 m；桥梁线密度mb=1 500 kg/m；1阶频率fb=1.8 Hz，1阶阻尼比为0.005。显然，该结构的1 阶频率与人行荷载的主频率十分接近，且结构阻尼比很小，人致荷载作用下很容易诱发结构的过量振动。

图2 结构平面尺寸(单位:m)

2.2 人群模型

基于式（1）中的社会力模型，采用Massmotion软件[21]进行人群运动行为模拟。模型中的行人视为单独的个体，朝着目标位置按照理想速度行进。假定行人的理想行进速度服从均值为1.34 m/s、标准差为0.26 m/s 的正态分布[4]。假定单人平均步长为0.75 m，则单人的理想步频均值为1.34/0.75=1.787 Hz。显然，在本算例给定的计算参数条件下结构可能产生共振。

计算过程中考虑不同人群密度的影响，人群密度ρm=0.1 人/m2～1.0 人/m2。ρm上限取为1.0 人/m2，主要是考虑到当ρm大于1.0 人/m2时，人群处于稠密状态，此时人员自由行走受限，步行荷载的动力效应很弱，结构动力响应不大，而布置障碍将影响人群的正常通行。

假定人群从结构左侧上桥，右侧下桥。桥面入口处的边界条件可在Massmotion软件中通过时间T内进入桥面的总人数Ntot进行设置，假定入口处人员的到达时间服从均匀分布。计算时T取为10倍的单个行人的平均过桥时间Tm，即T=10Tm=10L/vm，式中vm为行人的平均速度。通过将T取较长的时间保证桥面上的人群处于近似稳定状态，从而桥面总人数Ntot≌10ρmLD。

2.3 障碍布置方式

考虑如图1 所示的BN 和LS 两种障碍布置方式。为增加障碍布设的灵活性，采用非连续布设方案，并假定单个障碍尺寸（长度和宽度）相等，障碍宽度ld=D/10（D为桥面宽度）。对于BN 式障碍，给定障碍横向间距Bn=D/2（D为桥面宽度）；对于LS式障碍，假定障碍沿桥梁轴线纵向布置。

3 结果分析与讨论

3.1 障碍长度的影响

以单个障碍为例，研究障碍长度对人群平均步频的影响。假定障碍以桥跨中点为对称轴沿纵向对称布置，人群密度为0.4人/m2（对应稀疏人群）。

图3 给出了无障碍、设置单个BN 式障碍和LS式障碍时桥面人群密度分布图。

图3 桥面人群分布密度示意图（ρm=0.4人/m2）

显然，无障碍时人群分布较为均匀，且分布密度趋于设定值（0.4 人/m2）；当设置BN 式障碍时，人群在断面缩小处聚集，产生拥堵，局部密度增大，当人群通过障碍后密度逐渐趋于均匀；LS式障碍对人群的密度分布影响不大。图4进一步给出了桥面人数随时间的变化曲线。显然，随着时间的增加（当t＞100 s 时），桥面人数逐渐趋于稳定（对应密度ρm=0.4人/m2，桥面稳态人数N=ρmLD=120 人）。随着人群逐渐下桥，桥面人数逐渐减小直至为零。此外，比较图4中不同工况下人群（1 200人）过桥时间可知，与无障碍情况相比，当设置BN式障碍时，人群总过桥时间增加，说明人群平均行进速度显著下降；LS 障碍对过桥时间的影响相对较小。

图4 桥面人数随时间的变化曲线

对人群中所有个体通过桥面的平均步频进行统计，并绘制其概率概率分布图。图5 给出了人群密度为0.4人/m2时，所有行人（Ntot=10ρm LB=1 200人）步频的概率密度分布图。显然，各工况下人员的平均步频均服从标准正态分布。因此，后续分析中，对人群步频的统计分析均以均值和标准差的形式给出。无障碍情况下人群的平均步频最大，方差最小，概率密度曲线最为“陡峭”，布置LS式障碍对人群的干扰效果有限，BN式障碍下人群的平均步频大幅下降，也更为离散，其概率密度曲线更为平缓。

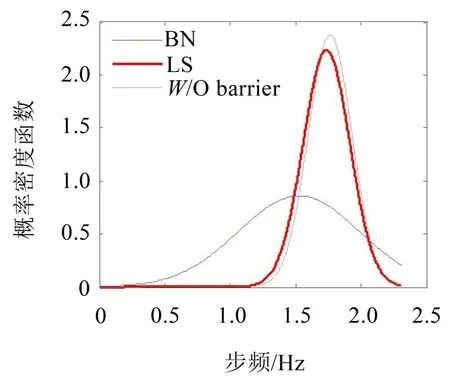
图5 人群步频的概率密度分布（ρm=0.4人/m2）

表1给出了不同障碍长度下人群行走步频统计值。由表1 可知，无论是在BN 式还是LS 式障碍条件下，人群的平均步频均对障碍长度变化不敏感，特别是当障碍长度小于10 m时。与无障碍组相比，LS式障碍对人群步行特征的影响很小；较LS式障碍而言，BN式障碍更为有效。此外，模拟结果表明，当障碍长度很小（如Ln=1 m）时，BN式障碍就能形成有效的阻塞，此时人群平均步频由1.776 Hz下降至1.689 Hz，标准差由0.156 Hz 上升至0.333 Hz。通过观察人员的行走过程发现，人员在断面收缩处出现阻塞，有效降低了人群的行进速率和步频。

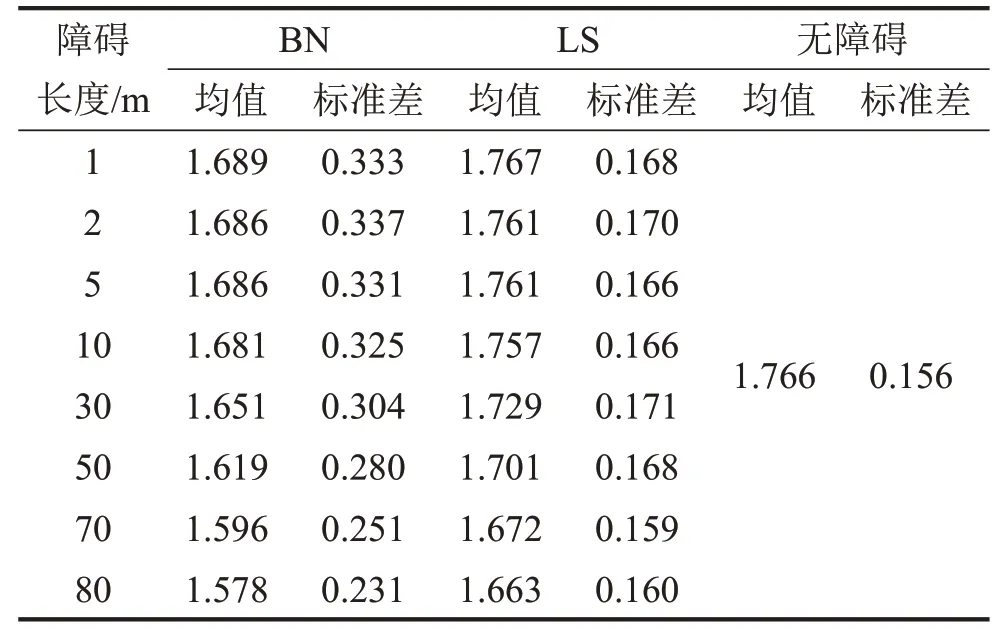
表1 不同障碍长度条件下人群行走步频统计值/Hz

3.2 障碍布置位置的影响

以单个障碍为例，研究障碍布设位置对人群平均步频的影响。障碍长度Ln=10 m；考虑图6所示x=11.667 m、28.334 m、45.000 m、61.667 m 和78.334 m 5 种布置位置(x为障碍起点距离桥面左侧入口的距离）；人群密度为0.4人/m2。

图6 障碍布置示意图

表2 给出了5 种障碍布置情况下人群步频的统计结果。显然，障碍的布置位置对人群的行走特征几乎无影响。LS式障碍对人群步频均值影响较小，BN式障碍效果较好。

表2 不同障碍布置位置条件下人群行走步频统计值/Hz

3.3 障碍纵向间距的影响

为考虑障碍纵向间距对人群行走步频的影响，给定计算参数如下：以桥跨中点为对称轴沿纵向对称布置两个障碍，单个障碍长度Ln=5 m，人群密度为0.4 人/m2，障碍纵向间距分别取为lw=1 m、2 m、3 m、4 m、5 m、10 m、20 m。

表3 给出了7 种障碍间距条件下人群步频的统计结果。显然，障碍间距对人群的行走特征影响很小，可以忽略。由表3可知，LS式障碍对人群步频均值影响较小，BN式障碍效果较好。

表3 不同障碍间距条件下人群行走步频统计值/Hz

3.4 障碍个数的影响

由于人群平均步频对障碍位置不敏感，假定障碍以桥跨中点为对称轴沿纵向对称布置，单个障碍长度Ln=5 m，障碍纵向间距为lw=5 m。不同障碍个数N对应的人群行走步频统计值列于表4。由表4可知，无论是BN式还是LS式障碍，随着障碍个数N的增加，人群的平均步频均逐渐下降，标准差逐渐增大并渐趋稳定。随着障碍个数N的增加，步频均值下降逐渐缓慢。通过增加障碍个数，可对人群的行走过程进行有效干预。本文研究表明，当N=5 时，BN式障碍已经可以起到较好的降低人群平均步频、增加人群步频离散程度的作用。此外，与BN 式障碍相比，LS式障碍对步频的阻碍很弱。

表4 不同障碍个数条件下人群行走步频统计值/Hz

3.5 人群密度的影响

为考虑人群密度ρm对人群行走步频的影响，给定计算参数如下：障碍个数N=5，单个障碍长度Ln=5 m，障碍纵向间距为lw=5 m。

表5列出了人群步频均值和标准差随人群密度ρm的变化情况。

表5 不同人群密度条件下行走步频统计值/Hz

图7 更为直观给出了3 种工况下人群步频均值随人群密度的变化曲线。显然，随着人群密度的增加，3种工况下的平均步频均逐渐下降。与无障碍情况相比，LS对步频的阻碍作用较为微弱，BN式障碍对人群平均步频的影响十分显著，曲线随密度增加逐渐下降且斜率十分陡峭。此外，在人群密度很小（如ρm=0.1 人/m2）的情况下，BN 式障碍就能起到一定的频率阻碍作用。

图8 中以BN 式障碍为例给出了桥面人员在密度分别为0.6 人/m2和1.0 人/m2时的分布情况。对于BN 式障碍，人群主要在障碍入口处聚集，平均密度越大，人群堵塞集度越大，当人群通过障碍后，人群密度又趋于均匀。

图8 BN式障碍在不同密度条件下的人群分布（N=5，Ln=5 m)

此外，图9 给出了布设单个BN 式障碍（以桥跨中点为对称轴沿纵向对称布置）时人群平均步频与密度的关系曲线。与图7 类似，随着人群密度的增加，人群的平均步频逐渐减小，各个体之间步频的离散程度增加，同频比率降低。当密度低于0.4 人/m2时，频率下降相对平缓；当密度大于0.4 人/m2时，随着人群密度的增大，平均步频下降加快，表现为曲线下降段更为陡峭，但步频标准差趋于稳定。

图9 平均步频与人群密度的关系曲线(N=1，Ln=5 m)

4 关于结论普适性的探讨

前文以图2 所示人行桥为例，分析了障碍布设对单向人流行走步频的影响。由于实际人行桥多为双向人流，限于篇幅，本节简要探讨人员流向及人行桥尺寸对结论普适性的影响。首先考虑双向人流，计算参数与障碍布设同3.5节。

图10给出了3种工况下双向人流步频均值随人群密度的变化曲线。所得结论与单向人流情况基本吻合。即，相较于影响较小的LS式障碍，BN式障碍对人群平均步频的影响更为显著，且在很小的人群密度下，BN式障碍就能起到一定的频率阻碍作用。

图10 平均步频与人群密度的关系曲线（N=5，Ln=5 m)

此外，为了验证人行桥平面尺寸对结论普适性的影响，考虑如下计算工况：人行桥长度L=60 m，宽度D=5 m；单个障碍长度Ln=3 m，宽度ld=0.8 m。以改变障碍个数的工况为例，所得计算结果如表6所示。

表6 不同障碍个数条件下人群行走步频统计值/Hz

由表6 可知，双向人流下的BN 式障碍与LS 式障碍的特征与3.4中结论相似。显然，本文的结论对于不同尺寸的人行桥均有普适性。

5 结语

本文从振源入手，通过布设障碍，人为干预人群的运动行为，降低人群的平均行走步频及同频比率，以避开结构的自振频率，进而减小结构的人致振动响应。重点研究了BN式和LS式障碍对人群行走步频的影响。主要结论如下：

（1）通过合理布设障碍，可有效降低人群的行走步频和同频比率，从而从源头上避开结构的敏感频率，起到减振的效果。此外，障碍布设法具有方式灵活、成本低、障碍容易安装和拆卸等优点，可供大跨度柔性空间结构的减振设计采用；

（2）BN式障碍较LS式障碍更为有效；

（3）BN 式和LS 式障碍对单个障碍长度、障碍布置位置、纵向间距不敏感，而对障碍个数较为敏感。根据本文算例，当障碍个数N=5 时，BN 式障碍已经可以起到较好的降低人群平均步频、增加人群步频离散程度的效果；

（4）BN 式障碍对人群的密度较为敏感。随着人群密度的增加，人群的平均步频逐渐减小，同频比率也随之降低。

本文仅研究了障碍布设对人群行走步频的影响，未进行后续的振动分析与减振计算，旨在从荷载源头上分析此种方法的减振潜力。对于大跨度柔性结构，人群与结构相互作用[22-23]是十分重要的课题，文中忽略了结构振动对人群行走特征的潜在影响以及人群生物力学特性对结构动力特性的影响，在今后的研究中将对此加以完善。