考虑任务行程时间的多载量自动导引车系统防死锁任务调度

武 星 翟晶晶 楼佩煌 胡 亚 肖海宁

1.南京航空航天大学机电学院，南京，2100162.盐城工学院机械工程学院，盐城，224051

0 引言

自动导引车(automated guided vehicle，AGV)是一种最具代表性的物流输送机器人，由多台AGV构成的AGV系统已广泛应用于各种制造系统以及仓储配送领域[1-3]。为了保证多台AGV在同一工作空间中有序运行，需要研究任务调度[4]、路径规划[5]和交通管控[6]三项核心的系统级使能技术。其中，AGV系统任务调度为：当系统中存在多个物料配送任务及空闲AGV时，在满足一定的约束条件下，确定各物料配送任务的执行顺序及其与空闲AGV的分配关系，使系统的某些性能达到最优。

针对AGV系统任务调度问题，当前国内外研究主要以单载量AGV为对象，其主要研究方法有：传统分析方法、建模与仿真方法、智能优化算法、混合优化方法[7-9]。相对于传统的每次装卸一个/组载荷的单载量AGV，多载量AGV(如一台牵引AGV拖带多个数量可变的挂车)可在一次物料配送任务中，分别从多个发料点进行多个载荷的装载，或到多个送料点进行多个载荷的卸载，显然具有更高的单车运输能力和更强的配送作业柔性。但目前关于多载量AGV任务调度问题的研究主要采用的是启发式规则，HO等[10-14]将多载量AGV系统任务调度问题分解为装卸载选择调度[11]、卸载点访问顺序调度[12]、装载点访问顺序调度[13]和装载任务选择调度[14]四个子问题，分别设计了相应的启发式规则。在此基础上，AZIMI等[15-17]借助计算机仿真工具分析了多种组合调度规则的实际调度效果，结合了线性回归、离散偶数模拟和线性整数规划三种数学方法，提出了一种用于优化多载量AGV系统吞吐量的启发式算法。LEE等[18]研究了系统资源配置对装载及卸载规则的影响规律。RAMANAIAH等[19]分析了启发式调度规则在不同导引路径布局下的性能表现。

上述研究主要关注设计多载量AGV系统任务调度规则或分析任务调度规则的实际调度效果，缺乏考虑应用环境中的各种约束条件，如多载量AGV装卸载顺序、AGV容量、工位缓冲区容量、配送截止时间等。大量实验结果表明[20-21]，忽略这些约束会使系统发生堵塞、死锁，从而显著降低整个调度系统的性能。AGV系统中的死锁可分为因缓冲区容量不足引发的缓冲区死锁以及因多个AGV之间路径冲突导致的环路死锁[22]。针对缓冲区死锁，XIAO等[23]提出了一种将死锁状态临界任务暂时禁止运行的死锁避免策略；KALINOVCIC等[24]通过禁止将工件送往已堵塞的工位来避免死锁，但保守的资源分配限制策略往往会降低系统运行效率。针对环路死锁，ZHAO等[25]提出了一种基于动态资源预留的多AGV调度和避碰方法；XIAO等[26]提出了一种基于交通序列优化策略的碰撞死锁预防方法，并通过仿真结果验证了上述方法的可行性和有效性。

实际上，环路死锁是AGV系统交通管控或路径规划时所需面临的问题，笔者所在团队已在文献[27]中进行了相关分析研究。而缓冲区死锁则是AGV系统任务调度时必须解决的重点和难点问题。因此，本文以多载量AGV系统为研究对象，针对某复杂军工产品装配线[27]下多载量AGV系统的任务调度和缓冲区死锁问题，建立了任务行程时间预测模型，提出了一种基于人工免疫-灰狼优化(artificial immune-grey wolf optimization，AI-GWO)算法的多目标防死锁任务调度方法。

1 总体方案

1.1 问题描述

该复杂军工产品的生产计划与物料配送过程既涉及机械、电气组件的外协与采购，也包含机械零部件、电子元器件、组件、套件等各种物料与在制品在不同车间、不同工位之间的配送、转运和出入库等。按照传统的装配生产线布局与装配人员工作安排，各工序操作现场分散，车间内部半成品周转耗时长，配送准时性差，装配工位可能待料停产。

针对传统配送准时性差的问题，考虑到装配工位物料种类多、配送要求差异性大的实际需求，本文采用多载量AGV在辅料库与装配工位之间配送标准机械零件和电子元器件，利用单载量AGV在半成品库与装配工位之间配送用于部装的套件、组件等。整条装配生产线包括：A舱部装线、C舱部装线和舱段总装线以及外协生产部装的B舱、D舱和E舱的三条输送线，装配生产线中的AGV系统采用单向导引路径网络。

装配线中每个工位都配有容量有限的关重件输入缓冲区、辅料输入缓冲区以及输出缓冲区。当某个工位需要物料时，AGV从物料仓库中装载物料，按照路径网络中的最优路径，在截止时间前将物料送往相应装配工位的输入缓冲区。当工位所需物料齐全后开始装配，装配完成后工件进入输出缓冲区。此时，装配工位向AGV调度系统发出工件搬运请求，依次输送到下一个工位或最终的成品库。为聚焦多载量AGV任务调度的研究，本文沿用文献[27]对物流配送过程的假设，并规定：多载量AGV从前往后依次装载挂车，并以先进后出的方式卸载挂车。

为保证整条装配线的高效有序运行，必须先保证各装配工位的装配物料准时配送。然而，各工位输入、输出缓冲区容量有限。当输出缓冲区中工件未及时运出时，工位会因输出缓冲区无剩余容量而堵塞；当装配物料未及时送达某工位时，工位会因物料缺乏而待产。因此，多载量AGV系统的任务调度需要确定物料配送任务执行顺序及其与空闲AGV的分配关系，并防止工位缓冲区死锁，从而保证AGV配送的准时性和装配物料的齐套性。

1.2 研究方案

为解决多载量AGV系统的任务调度和缓冲区死锁问题，本文构建了包含实际应用约束的任务调度模型，提出了一种考虑任务行程时间的多载量AGV系统任务调度方案，如图1所示，图中蓝色底纹所示内容为本文所要研究的关键内容。

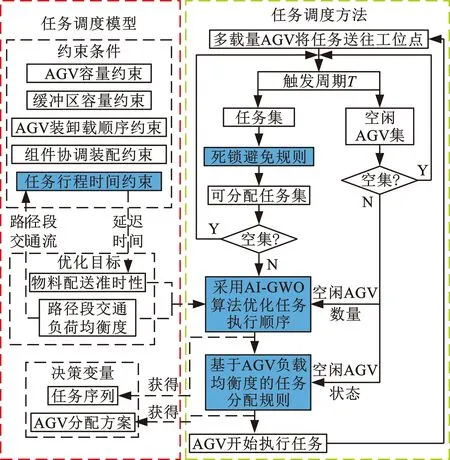
图1 总体方案Fig.1 General scheme

在任务调度模型中，多载量AGV装卸载顺序、AGV容量、工位缓冲区容量等约束相对易于建模，而任务行程时间因具有动态性和不确定性而难以预测，该约束还会直接影响准时性优化目标。因此，首先针对AGV运动特性和交通延误规律，构建任务行程时间预测模型。为了求解得到最优的任务执行序列和AGV分配关系以及避免缓冲区死锁，本文提出了一种带防死锁策略的任务调度优化方法，利用死锁避免规则禁止即将引发工位缓冲区死锁的任务运行，基于AI-GWO算法优化任务执行顺序，根据AGV负载均衡度进行配送任务分配。

2 任务调度建模

2.1 任务调度模型

多载量AGV调度是一个需要考虑多目标的数学建模问题。如图1所示，本文以关重件、辅料等动态配送任务执行序列及其AGV分配方案为决策变量，以物料配送准时率和路径段交通负荷均衡度为综合优化目标，并以任务行程时间、物料缓冲区容量、AGV装卸载顺序、组件协调装配等为约束条件构建任务调度模型。其中，该模型的目标函数为

(1)

(2)

式中，f1为物料配送延迟率；f2为交通负荷不均衡度(即路径拥堵率)；R为物料配送任务总数(即可分配任务的总数)；De为第e个物料配送任务的延迟状态；qi为第i条路径上的车辆平均长度；s1i为第i条路径段的长度；I为

(3)

(4)

其中，Te为第e个物料配送任务的延迟时间，其表达式为

Te=de-(Se+TCe)e=1，2，…，R

(5)

式中，de为第e个物料配送任务的交付时间；Se为第e个物料配送任务的开始时间；TCe为第e个物料配送任务的任务行程时间。

在任务调度模型中，任务行程时间因具有动态性和不确定性而难以预测，它不仅与单台AGV所通过的运行路径有关，还与整个系统的路网交通状态有关，因此，本文将任务行程时间分解为自由行程时间与交通延误时间，并建立相应的时间预测模型。

2.2 任务行程时间预测模型

任务行程时间分为自由行程时间和交通延误时间两部分。前者是指在没有其他AGV干扰的情况下，单台AGV在路径网络中的自由运行时间。后者是指由于受路网交通流分布及交通管控策略的影响，单台AGV通过路径网络额外所需的等待时间。

2.2.1自由行程时间预测模型

自由行程时间受运行路径、AGV 运动速度、装卸载时间等多种因素的共同影响。对于不同类型的AGV，各影响因素也存在较大差异。在运行路径方面，单载量AGV每次只配送一种零部件，其运行路径取决于该零部件的装卸载工位点。然而，多载量AGV每次输送多节拖车，其运行路径不仅取决于所有拖车的装卸载工位点，还与拖车的装卸顺序密切相关，远比单载量AGV的情况复杂。此外，AGV运动速度也非恒定值，受AGV运动学及动力学特性(执行速度、转弯速度、加减速特性等)、运行路径段特征(单路径段、直行路口、转弯路口等)、承载状态(空载、满载、拖车类型等)等众多因素的共同影响。为此，本文将所有装卸载工位点之间的最优单向路径分解为典型路径段，在考虑AGV加减速特性的情况下，假设AGV在路径段、直行路口、转弯路口的速度标量分别为v1、v2、v3，单载量AGV与多载量AGV自由行程时间的计算方法具体如下。

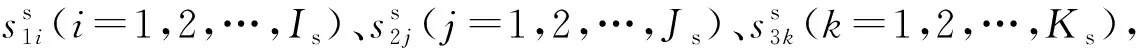
(6)

(7)

(8)

其中，γ为单载量AGV的速度因子。假设单载量AGV当前的负载量和额定负载量分别为Fs、Fes，单载量AGV负载系数为α，则

(9)

(10)

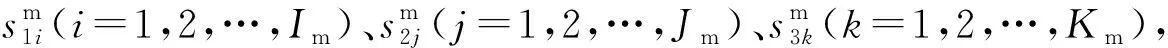
(11)

(12)

(13)

其中，δ为多载量AGV的速度因子。假设多载量AGV经过某路径段、直行路口或转弯路口时拖车的编号和数量分别为p、P，第p个拖车的速度因子为εp，则

(14)

(15)

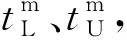
(16)

2.2.2交通延误时间预测模型

在AGV任务执行过程中，交通延误时间的影响因素包括AGV拖车的长度、AGV之间的安全距离、单路径段长度等。由于交通延误时间受路网交通流分布及交通管控策略的共同影响，则它主要体现为因路径堵塞而导致的路口等待时间。假设从当前任务装载到卸载期间所需经过的直行路口、转弯路口的数量分别为S和C，所需经过的直行路口、转弯路口的编号分别为s和c，所经过的第s个直行路口的长度和第c个转弯路口的长度分别为s2s、s3c，某AGV到达路口时已在路口排队的AGV编号和数量分别为a、A，则根据已在路口排队的第a辆AGV的长度la和安全距离系数β(通常取值为0.6～1.0，本文取0.8)可以得出该AGV在直行路口和转弯路口的累积延误时间t2d、t3d分别为

(17)

(18)

其中，τa为已在路口排队的第a辆AGV的速度因子，其表达式为

(19)

则任务的交通延误时间为

Td=t2d+t3d

(20)

2.2.3任务行程时间预测模型

由于任务行程时间包含任务自由行程时间与交通延误时间，因此根据式(10)、式(16)、式(20)可得第e个物料配送任务的任务行程时间TCe为

TCe=Tf+Td

(21)

根据任务行程时间数学模型，可确定待分配任务的执行时间，并对任务进行排序和分配。然而，多载量AGV系统任务调度除了要考虑任务行程时间外，还需考虑环路死锁、路径交通流等系统约束。因此，本文针对上述多目标任务调度模型，研究了求解任务最优执行序列及其AGV分配方案的多目标优化方法。

3 任务调度优化方法

大多数已有研究的调度系统主要针对单载量AGV，通常采用基于启发式规则的调度方法以降低问题复杂性。然而，本文研究的多载量AGV系统任务调度问题更加复杂，启发式调度规则已不能满足要求。

为了求解多载量AGV系统任务调度问题，本文结合人工免疫(AI)算法与灰狼优化(GWO)算法的优点，提出了一种基于人工免疫-灰狼优化(AI-GWO)算法的混合多目标优化方法。首先考虑工位缓冲区的容量，利用死锁避免规则暂时禁止引发死锁的任务运行，然后采用AI-GWO混合多目标优化方法确定任务的执行顺序，最后基于负载均衡度进行空闲AGV的任务分配，以提高系统的任务准时率和路径段的交通负荷均衡度。AGV任务调度的主要流程如下：

(1)当系统达到一个定时周期T时，进入步骤(2)。

(2)统计系统中所有的物料配送任务和空闲AGV，分别构成待分配任务集和待调度AGV集。若待分配任务集或待调度AGV集为空集，则转步骤(1)；反之，则进入步骤(3)。

(3)计算各工位的剩余容量和系统的可利用载量，根据死锁避免规则从待分配任务集中去除被禁止的任务，未被禁止的任务构成预分配任务集。若预分配任务集为空集，则转步骤(1)；反之，则进入步骤(4)。

(4)计算预分配任务的数量RC和待调度AGV的总载量G。若RC≤G，此时预分配任务集即为可分配任务集，并进入步骤(6)；反之，则进入步骤(5)。

(5)根据任务紧迫度进行排序，选择紧迫度排名前G的任务构成可分配任务集，并进入步骤(6)。

(6)采用AI-GWO混合多目标优化方法对可分配任务集进行任务排序，并进入步骤(7)。

(7)根据待调度AGV的工作负载状态，将排序好的任务优先分配给负载总量低的空闲AGV，并更新系统工位和AGV状态后转步骤(1)。

3.1 死锁避免规则

工位缓冲区死锁是指以下情形：当某工位及其输入缓冲区、输出缓冲区都被工件占满时，若无AGV运离其输出缓冲区的工件，则运送工件到输入缓冲区的AGV因无法获得释放空间而一直等待卸载，该状态称为工位缓冲区堵塞。若所有AGV都处于这种堵塞状态，则整个系统进入工位缓冲区死锁，这将严重影响物料运送效率与任务准时率。

为避免工位缓冲区死锁，笔者提出了多载量AGV死锁避免方法[28]。根据每辆AGV的堵塞任务数得到AGV可利用载量，对于可利用载量不大于死锁临界值(本文取4)的AGV，禁止分配同时满足以下两个条件的任务：①起始工位剩余容量大于或等于0；②目标工位剩余容量小于或等于0。

所有未被禁止的任务构成预分配任务集。如果预分配任务的数量RC大于待调度AGV的总载量G，则存在RC-G个任务缺乏空闲AGV进行搬运。为了保证任务准时率，以交付时间de来评价任务紧迫度，距离交付时间越近，任务越紧急。因此，在预分配任务集中选取交付时间de排名前G的物料配送任务构成可分配任务集。

3.2 任务排序优化算法

本文提出的AI-GWO混合多目标优化方法的具体流程如图2所示。

图2 AI-GWO算法流程Fig.2 AI-GWO algorithm flow chart

(1)编码。采用任务排序为算法编码，可表示为B={b1，b2，…，br，…，bR}，其中r为任务br在所有可分配任务排序中的位置，R为可分配任务的总数。然后将B中元素依据排序位置(从前至后)和AGV的载量Av分成Z=RoundUp(R/Av)簇，以便于按簇将任务分配给AGV，其中RoundUp(·)表示向上取整函数。例如：假定系统中可分配任务序号为任务1至任务7，各任务的排序位置如表1所示，则对应的编码B={5，3，6，1，7，4，2}，若多载量AGV的载量Av=4，则任务1至任务7可被分成2簇，其中{5，3，6，1}被分配给空闲AGV1，{7，4，2}被分配给空闲AGV2。

表1 可分配任务集及排序示例

(2)种群初始化。在种群初始化过程中，选取可分配任务的总数R作为种群规模。为了尽可能地将所有卸载工位点距离相近的任务分配给同一辆AGV，本文采用最大最小距离聚类算法[29]对前R/2个种群进行种群初始化，其余种群随机产生。

(3)适应度计算。根据物料配送准时率(即1-f1)和路径段交通负荷均衡度(即1-f2)，构建多目标优化的种群适应度函数，其表达式为

F=wa(1-f1)+wb(1-f2)

(22)

其中，wa、wb为两个目标的权重系数，其取值由仿真分析获得。

(4)社会等级分层。GWO算法优化中最核心的操作是确定种群中最佳的三个个体，并让其带领其他个体往最优解方向进行搜索。根据个体适应度从高到低的排序，将适应度前三的灰狼个体设置为α狼、β狼、δ狼，并以它们为首领对其他灰狼位置进行更新。

本研究中混合式学习班及传统授课班期末均采用手机在线无纸化测试，按照试题库随机选题的方式进行考核，题型、题量及难易程度相当于助理会计师考试，试卷采用百分制，考核结果显示，两种授课班级平均成绩分别是58.46分和47.75分，混合式学习班成绩高于传统授课班级22.45%；但最高、最低成绩均出自于传统授课班级，我们认为这可能与个别同学的基础和个人的努力有关，不影响混合式学习的优势。

(5)位置更新操作。GWO算法虽然具有较好的搜索性能，但随着迭代次数的增加，容易陷入局部最优。因此，本文采用AIA算法的克隆变异操作进行种群位置更新，以增加种群多样性，避免算法过早收敛。按照适应度从高到低排序选择R1个(R1=R/4)精英个体进行克隆变异。其中，由社会等级分层得到的α狼、 β狼和δ狼必须参加克隆变异操作。

克隆操作如下：克隆精英种群中的所有个体并得到新的克隆种群，克隆后种群规模RG的表达式为

(23)

其中，g为精英种群中个体的编号；R1为精英种群规模，克隆种群种群规模RG与R1成正比；Round(·)表示取整函数；φ为0～1之间的随机数；Eg为精英个体g在降序排列的精英种群中的序位。由于精英个体在种群中的序位是按个体适应度的高低排列的，因此精英种群中每个个体克隆的数量与个体自身的适应度有关。并且式(23)可以确保精英种群中的每个个体都有一定数量的克隆体。

变异操作如下：变异算子可以增加种群的多样性，防止算法陷入局部最优解，本文对常用的高斯变异算子进行了改进，表达式为

(24)

因为种群个体中每个基因在基因排序中的位置(即可分配任务的排序位置)为1～R中的不重复正整数，所以新基因在高斯变异后需要进行取整和取余操作，并形成临时子代。为了保证临时子代每个基因的排序不重复，临时子代的基因需从第一个基因到第R个基因依次调整：若待调整基因与变异成功的基因不重复，则变异成功；否则舍弃此结果，并根据相近原则从1～R中选择一个与前面结果不重复的整数作为该基因的变异结果。临时子代个体经过基因调整后可成为种群子代个体。

变异算子是通过采取某种基因突变的方式来实现局部搜索的，然而单级变异(即只进行一次变异操作)的搜索范围较小，不容易跳出局部最优解，因此，本文提出了一种多级变异策略，即以单级变异形成的子代为多级变异的父代，再次执行变异操作形成新的子代，并从单级变异与多级变异的子代中选择最优的子代作为该次变异操作的子代。由于多级变异会消耗更多的资源，因此只有陷入局部最优解时才启用多级变异策略。本文以迭代次数来评价算法是否陷入局部最优解，当迭代次数φ≤50时，采用单级变异；当迭代次数φ>50时，则采用多级变异策略，该策略可以增加种群多样性，促进算法寻找全局最优解。

(6)精英保留策略。将种群规模为R的父代种群和种群规模为RG的子代种群合并为一个大小为R+RG的新种群。在新种群中，对适应度相同的个体进行拥挤距离[30]排序，从中选择出最优的R个个体作为下一代的父代种群。

(7)终止条件。若种群规模不同，则得到最优解的迭代次数也不同。为了在得到近似最优解的同时避免算法陷入无限循环，本文以完成100次迭代过程为终止条件。

3.3 任务分配规则

可分配任务经过排序后，本文采用AGV负载均衡度评价方法进行任务分配。首先计算每个空闲AGV已搬运完成的任务总距离，并按照搬运总距离升序的方式进行排列，将可分配任务按簇方式优先分配给搬运总距离小的AGV。

4 仿真实验

4.1 仿真模型创建

为验证本文防死锁任务调度方法的有效性，采用仿真软件Plant Simulation创建装配线物流系统的仿真模型，仿真界面参见文献[27]。AGV和导引路径分别使用Transporter和Track对象表示，工位点的输入缓冲区、工位、输出缓冲区分别用Buffer、SingleProc和Store对象表示。工位点功能通过在Track对象增加Sensor对象来实现，各种任务调度方法通过在Method对象中编制Simtalk程序来实现。多载量AGV系统的生产节拍为15 min，装配工位点的输入、输出缓冲区容量为4，多载量AGV载量Av=4，AGV在各情况下的运行速度为：v1=1 m/s，v2=0.5 m/s，v3=0.5 m/s。仿真运行时，通过统计任务状态来分析任务调度方法的性能(如求解速度、收敛性能等)。

4.2 仿真实验数据分析

4.2.1任务行程时间预测实验

任务行程时间受到AGV运动特性、任务路程、路网交通流等多因素影响，其中，路网交通流与路径网络中并发运行AGV的数量有关，AGV数量越多，路径段交通流越大。因此，本文通过对比不同AGV数量下某一物料配送任务的任务行程时间预测值与实际值，以验证上述任务行程时间预测模型的准确性，实验结果如表2所示。

表2 任务行程时间预测实验

由表2可知，当系统中AGV数量较少(小于或等于10辆)时，任务行程时间预测值与实际值相同，说明当路径网络交通不太拥堵时，预测模型的准确度很高。然而，随着系统中AGV数量的增加(大于10辆)，任务行程时间预测值与实际值的误差逐渐增大，但预测误差最大不超过1%，且该误差不随AGV数量的增加而持续增大。实际上，该误差主要来源于当发生拥堵时AGV需要与调度控制系统频繁通信而耗费的时间。可见，上述任务行程时间预测模型是有效的。

4.2.2任务调度实验

为了验证本文任务调度方法的有效性，将AI-GWO算法与传统的遗传算法(GA算法)、GWO算法进行了对比，以适应度值来衡量各算法性能。本文以GA算法为优化方法，通过仿真得到了适应度计算公式(式(22))中的权重系数wa、wb。假设某个调度周期内，空闲AGV的数量为8，可分配任务数量为32(即种群规模为32)，算法的交叉概率为0.6，变异概率为0.2，分别设置5组取值不同的权重系数，实验结果如表3所示。

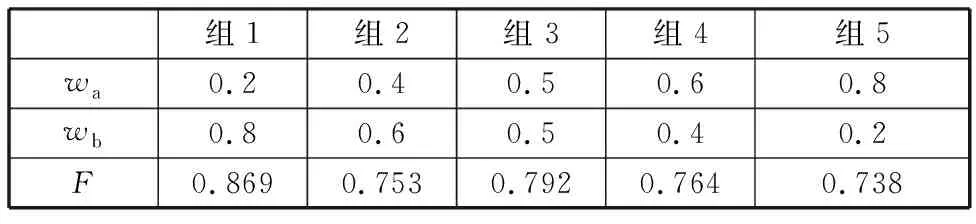
表3 不同wa和wb取值下的适应度值

由表3可知，当wa、wb的取值分别为0.2、0.8时，种群的适应度值最高，此时系统的任务准时率和路径段的交通负荷均衡度达到较优值。因此，本文取该组权值计算适应度。

为了比较三种算法的调度效果，本文采用缓冲区死锁避免规则设置了4组不同的可分配任务数和空闲AGV数量，如表4所示，采用仿真软件Plant Simulation进行装配线物流系统的运行仿真，各算法的适应度最优解如图3所示。

表4 系统环境参数

图3 各算法的最优解Fig.3 The optimal solution of each algorithm

由图3可知，当系统中任务数量与AGV数量较少(可分配任务数不超过24)时，GA算法、GWO算法和AI-GWO算法求解出的最优解是相同的，此时系统的任务调度问题比较简单，说明所提新算法在处理小规模调度问题时优势不突出。然而，随着系统中任务数量和空闲AGV数量的增加(可分配任务数大于24时)，相对于传统的GA算法和GWO算法，本文AI-GWO算法所获得的最优解适应度值最高，所以准时率最高、路径拥堵率最低。因为随着多载量AGV系统任务调度问题复杂化，传统的GA算法和GWO算法容易陷入局部最优解，而AI-GWO算法具有较强的全局寻优能力，用于求解较大规模的多载量AGV调度问题是有效的。

为了比较三种算法的收敛性能，以表4中第3种环境参数为例，采用仿真软件Plant Simulation进行装配线物流系统的运行仿真，适应度值收敛曲线见图4。

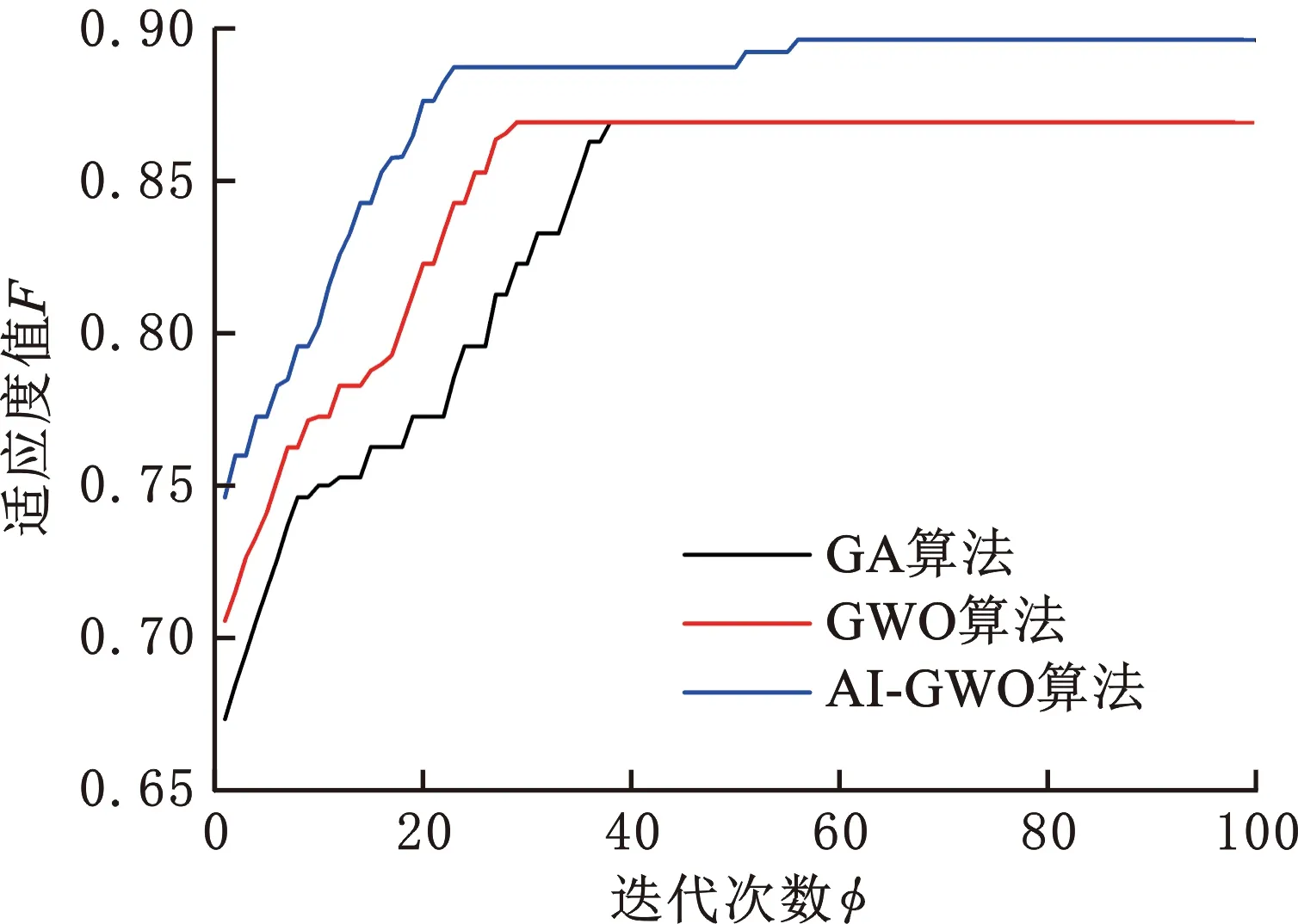
图4 适应度值收敛曲线Fig.4 Fitness value convergence curve

由图4可知，当系统可分配任务数为32和空闲AGV数量为8时，AI-GWO算法较传统GA算法和GWO算法具有更好的收敛速度和寻优能力。在前40次迭代过程中，AI-GWO算法采用最大最小距离聚类算法初始化，这有利于该算法更快地寻找到最优解。在迭代后期，GA算法和GWO算法均陷入局部最优解，而AI-GWO算法在迭代50次后使用多级变异，具有更强的全局寻优能力，足以跳出局部最优解的限制，有利于搜索适应度更高的个体。并且，与传统的GA算法和GWO算法相比，AI-GWO算法的最优解适应度值提高了3%以上，进一步表明该算法具有更强的全局寻优能力。

为进一步比较三种算法的运行速度，在第3种环境参数条件下，通过软件仿真获取算法的实际运行时间，实验结果如表5所示。

表5 算法运行时间

由表5可知，AI-GWO算法较传统的GA算法和GWO算法具有更快的运行速度，分别提高了约22%和31%。这将有利于提高整个AGV调度控制系统的实时性和运行效率。

5 结语

针对多载量AGV复杂任务调度控制问题，本文以最小化延迟率和交通负荷不均衡度为目标，建立了任务调度模型；分析了任务调度中的实际约束，并针对任务行程时间约束构建了预测模型；针对任务调度模型提出了一种基于人工免疫-灰狼优化(AI-GWO)算法的多目标防死锁任务调度方法，利用死锁避免规则禁止即将引发工位缓冲区死锁的任务运行，并融合AI-GWO算法对任务执行顺序进行多目标优化；最后根据AGV负载均衡度进行AGV任务分配，以提高系统的准时率和路径段交通负荷均衡度。仿真结果表明，AI-GWO算法具有较好的寻优能力和收敛速度，相比传统的遗传算法(GA算法)和灰狼优化算法(GWO算法)，AI-GWO算法的运行速度分别提高了约22%和31%，可以保证系统的准时率，防止系统发生堵塞。