氚深度分布对β射线诱发X射线光谱法测量能谱中Ar(Kα)强度的影响

陈 杨，陈志林，杨 阳，瞿金辉，程胜寒，李 余

(中国工程物理研究院核 物理与化学研究所，四川 绵阳 621900)

氚是未来聚变堆主要的燃料之一，ITER(国际热核聚变实验反应堆)中将循环处理多达2～3 kg的氚，进入真空室的氚也在102g量级[1]。在真空室中，等离子体会直接轰击偏滤器的靶板，预计将在其中滞留数g的氚，等离子体和PFMs(面向等离子体材料)相互作用产生的溅射产物也会与氘氚结合形成共沉积层，滞留在真空室室壁上；在相应的处理设施中，氚会通过渗透和扩散的方式进入结构材料中[2]。大量氚在PFMs和结构材料中的滞留，将影响聚变装置的安全稳定运行，也将直接影响结构材料的操作安全和服役寿命[3]。为燃料衡算和人员安全，有必要对滞留在材料中的氚进行准确测量，以研发更合适的材料和回收滞留氚的方法。迄今为止，已开发了诸如离子束分析[4]、LIBS(激光诱导击穿光谱法)[5]、金属化学蚀刻法[6]、成像板法[7]和BIXS(β射线诱发X射线光谱法)[8]等技术用于测量材料表层氚的含量或分布。BIXS由于具有无损和探测深度大的特点，还可区分表层和基体中的氚，近二十年来逐渐获得重视，也被ITER采用为候选技术之一。

BIXS的原理是使用超低能X射线探测器测量氚衰变产生的β射线和材料相互作用产生的轫致辐射和特征X射线的能谱，其中就包含了材料中氚的信息[9-10]。Matsuyama等[11]在样品和探测器之间引入氩气，通过测量材料表层的氚发出的β射线与氩气相互作用诱发的X射线来确定表层的氚含量，这样改进后测得的能谱中就包含了Ar在2.95 keV(Kα)和3.15 keV(Kβ)的两个特征峰。也就是说，只要结合β射线在材料中的衰减规律和Ar特征峰(特别是能谱中高且尖的Kα)的强度，一定程度上就可确定样品表面在β射线射程范围内的氚含量。氚衰变产生的β射线平均能量为5.7 keV，最大能量为18.6 keV，由于能量较低所以其在材料中的射程也相对较短，有机物中为～1 μm，金属中为～0.1 μm[12-13]。如果在β射线射程范围内连续分布着一定形式的氚，则使用BIXS方法测得的能谱中Ar(Kα)的强度与这个范围内的氚含量有着简单的线性关系，Matsuyama等[14]考虑了光电效应、X射线的吸收等影响，确定了每个电子3.1×10-4个光子的本征转换效率。毛莉等[15]详细研究了材料表面粗糙度对BIXS测量结果的影响，并对氚在材料体中深度分布反演方法开展了深入研究；杨阳等[16]研究了氚在样品中的面分布对BIXS能谱的影响。在前期研究中，对于在氩气中诱发X射线的材料表层氚的分布，均采用均匀分布，并未研究该层氚的分布对结果的影响。低能β射线在材料中衰减迅速，位于射程末端的氚可能对Ar(Kα)强度的贡献很小，将氚在材料表层的分布视作均匀将会对结果带来一定误差。本文主要计算氚在5种典型材料表层(β射线射程范围内)不同位置时β射线诱发的Ar(Kα)强度，量化不同位置的氚对总Ar(Kα)强度的贡献，并计算在4种典型的氚分布形式下Ar(Kα)强度的差异。

1 研究方法

本文关注β射线射程范围内氚的深度分布对BIXS测量中Ar(Kα)强度的影响，将分两个部分对其进行研究。BIXS方法测得的Ar(Kα)强度是所有在β射线射程范围内的氚贡献的总和，由于不同位置的氚衰变产生的β射线穿透到氩气中的情况不同，所以可通过对其量化，研究不同位置氚对总强度的贡献。为获得氚在不同位置时的Ar(Kα)强度，将射程范围内的样品分为一定厚度的薄层，通过计算就可获得各薄层中β射线诱发的Ar(Kα)强度和其对总Ar(Kα)强度的贡献。另外，以往在测量或计算过程中通常认为氚在材料β射线射程范围内的分布是均匀的，但实际上即使是在这样小范围内氚的深度分布也有各种形式，可通过在射程范围内的样品中设置几种典型的氚深度分布形式的方法，比较不同深度分布形式下Ar(Kα)强度的差异。

1.1 β射线射程范围内各位置氚对Ar(Kα)强度的贡献

首先可通过式(1)[17]得到低能电子在不同单质中的外推射程Rex。式中：A为质量数；Z为原子序数；T为电子的动能；m为电子静止质量，求得的Rex单位为g/cm2。外推射程的大小介于投影射程和最大穿透深度之间，可作为设置射程的参考。

Rex=a1[(1/a2)ln(1+a2τ)-

a3τ/(1+a4τa5)]

(1)

a1=0.233 5A/Z1.209

a2=0.000 178Z

a3=0.989 1-0.000 3Z

a4=1.468-0.011 8Z

a5=1.232/Z0.109

τ=T/mc2

将β射线射程范围内的样品从上至下分为若干个薄层，如图1所示，使用蒙特卡罗程序计算每个薄层中β射线穿透到氩气并与之相互作用产生的Ar(Kα)强度，就可获得氚在不同位置时Ar(Kα)的强度和每个薄层中氚对总强度的贡献。

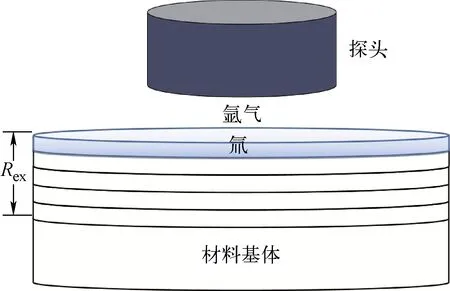
图1 样品分层示意图Fig.1 Diagram of sample stratification

1.2 连续不均匀的氚分布形式对Ar(Kα)强度的影响

氚进入材料的方式通常有吸附扩散和离子注入两种方式，吸附扩散进入材料的氚首先在材料表面吸附和聚集，然后沿浓度梯度在材料内部扩散，通常呈现递减的深度分布形式；离子注入的氚能到达材料内部的深度与其入射方向和能量以及材料类型有关，若是使用一定能量的离子束注入，氚会在某个深度附近聚集，随着时间推移，氚将向两侧扩散，呈现在某个深度集中，一侧递增、一侧递减的分布形式。在样品的β射线射程范围内分别设置随着深度均匀、二次集中、指数递减和指数递增的4种氚深度分布形式，使用蒙特卡罗程序计算Ar(Kα)的强度，就可比较不同深度分布形式对Ar(Kα)强度的影响。

2 结果和讨论

2.1 测量模型的建立

使用MCNP5按照真实的实验条件建立BIXS测量模型，样品表面距HPGe(高纯锗探测器)探头5 mm，之间充有常压的氩气，测量室的支撑材料为玻璃，铍窗厚度为3 μm，圆柱形的锗晶体的有效区域厚4.4 mm、半径4 mm、距铍窗1.5 mm，模型如图2所示。样品的材料分别为316LSS(不锈钢)、锆、CFC(碳纤维复合材料)、5083铝合金和钨，这些样品均是半径为1 cm的圆柱形薄片。氚β射线在5种典型材料中的外推射程分别为0.87、1.08、4.00、2.55、0.32 μm。将样品β射线射程深度范围内的表层分为若干个薄层，每次只计算在同一薄层内的β射线，氩会被从薄层中穿透出的β射线激发并产生特征X射线，记录其强度。

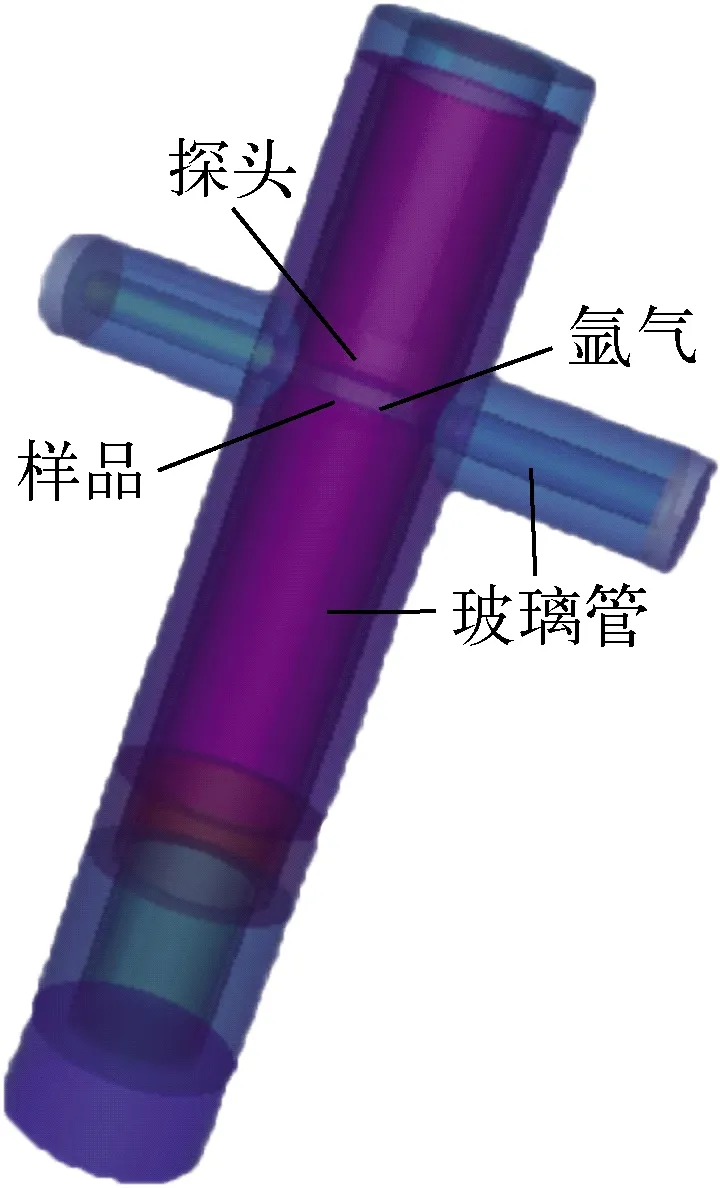
图2 MCNP计算模型Fig.2 MCNP calculation model

在MCNP5中，电子输运问题和电子在厚靶中运动产生轫致辐射的问题需用到电子与物质相互作用的数据，电子的数据库由ZAIDs以ZZZ000.nnE形式标识，包含el(截止至.01e结尾的ZAID)和el03(截止至.03e结尾的ZAID)。由于电子在输运过程中损失能量的方式以长程库仑力相互作用为主，导致电子损失相同能量所需进行的计算较光子和中子多几个量级，极大增加了计算时间。为简化计算，MCNP5使用了几个重要的理论，包括Goudsmit-Saunderson的角偏转、Landau的能量损失涨落以及Blunk-Leisegang对Landau理论的改进，这些理论使用了大量的近似，在MCNP中，使用多重散射理论将电子的多个能量损失累计成一次计算的影响，即“condensed history”。

2.2 不同材料中各薄层β射线诱发的Ar(Kα)强度

将在β射线射程范围内的样品均匀分成数个薄层。

316LSS样品的计算结果如图3所示。对于316LSS样品，表层总共分为8个薄层，每层厚度为0.1 μm，计算结果表明，第1层强度为7.23×10-6(±1.2%)，占总强度60%，第8层强度为2.37×10-8(±19.6%)，占总强度0.2%，第1层强度是第8层的305倍。

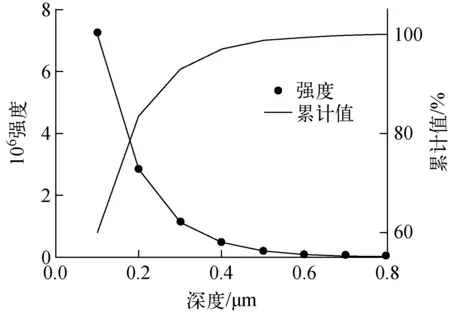
图3 316LSS样品各层的Ar(Kα)强度和累计值Fig.3 Ar(Kα) intensity and accumulative value of each layer of 316LSS sample

此外，还计算了锆、CFC、5083铝合金、钨样品中氚在表层分布的影响情况。在锆样品的计算结果中，第1层强度为8.30×10-6(±1.1%)，占总强度52%，最后的第10层强度为2.91×10-8(±17.7%)，占总强度0.2%，第1层强度是第10层的285倍。在CFC样品的计算结果中，第1层强度为6.78×10-6(±1.2%)，占总强度44.5%，第10层强度为2.82×10-8(±18%)，占总强度0.2%，第1层强度是第10层的240倍。在5083铝合金样品的计算结果中，第1层强度为7.45×10-6(±1.1%)，占总强度47.9%，最后1层第10层强度为2.73×10-8(±18.3%)，占总强度0.2%，第1层强度是第10层的273倍。在钨样品的计算结果中，第1层强度为8.83×10-6(±1.1%)，占总强度53.3%，最后1层第10层强度为3×10-8(±17.4%)，占总强度0.2%，第1层强度是第10层的294倍。

不同材料的计算结果显示，一系列相同厚度薄层的位置和Ar(Kα)强度符合指数衰减的规律，样品中第1层和第10层的计算结果之间会有接近300倍的差异。5种材料均存在相似的计算结果，这种结果是由于激发Ar(Kα)需能量在2.94 keV以上的粒子，一方面氚β粒子的平均能量仅5.6 keV，最大能量仅18.6 keV，以最大能量的β粒子射程进行计算时，内表层的大部分β粒子实际上均无法运动到材料表面与氩气作用，另一方面在与材料相互作用的过程中，β粒子损失动能，使得内表层的多数电子即使运动到氩气中也没有足够的能量激发Ar(Kα)。所以，实际上Ar(Kα)的总强度很大程度上是由最表面的那部分氚提供的，计算结果表明，在均匀分布氚的情况下，1/10射程内的氚贡献了约1/2的Ar(Kα)的强度。

2.3 不同氚深度分布形式下β射线诱发的Ar(Kα)强度

在5种材料中分别计算了β射线射程范围随深度呈二次集中型、指数递减型和指数递增型3种典型氚分布形式下的Ar(Kα)强度，并与均匀分布的情况进行对比，4种分布的概率密度函数如图4所示。

以氚均匀分布形式下的Ar(Kα)强度为标准进行对比，在316LSS样品β射线射程范围内不同分布的计算结果如图5所示。

计算结果表明，对于316LSS，均匀、二次集中型、指数递减型和指数增加型的计算结果分别为1、0.6、2.96和0.11，指数递减型的计算结果是递增型的27倍，集中在中部的二次分布和均匀分布计算结果相差40%。

另外4种材料也获得了类似规律。在锆样品β射线射程范围内，均匀、二次集中型、指数递减型和指数增加型的计算结果分别为1、0.62、3.06和0.12，指数递减型的计算结果是递增型的26倍，集中在中部的二次分布和均匀分布计算结果相差38%。在CFC样品β射线射程范围内，均匀、二次集中型、指数递减型和指数递增型的计算结果分别为1、0.71、2.77和0.14，指数递减型的计算结果是递增型的20倍，集中在中部的二次分布和均匀分布计算结果相差29%。在5083铝合金样品β射线射程范围内，均匀、二次集中型、指数递减型和指数递增型的计算结果分别为1、0.67、2.93和0.13，指数递减型的计算结果是递增型的23倍，集中在中部的二次分布和均匀分布计算结果相差33%。在钨样品β射线射程范围内，均匀、二次集中型、指数递减型和指数递增型的计算结果分别为1、0.57、3.04和0.11，指数递减型的计算结果是递增型的28倍，集中在中部的二次分布和均匀分布计算结果相差43%。

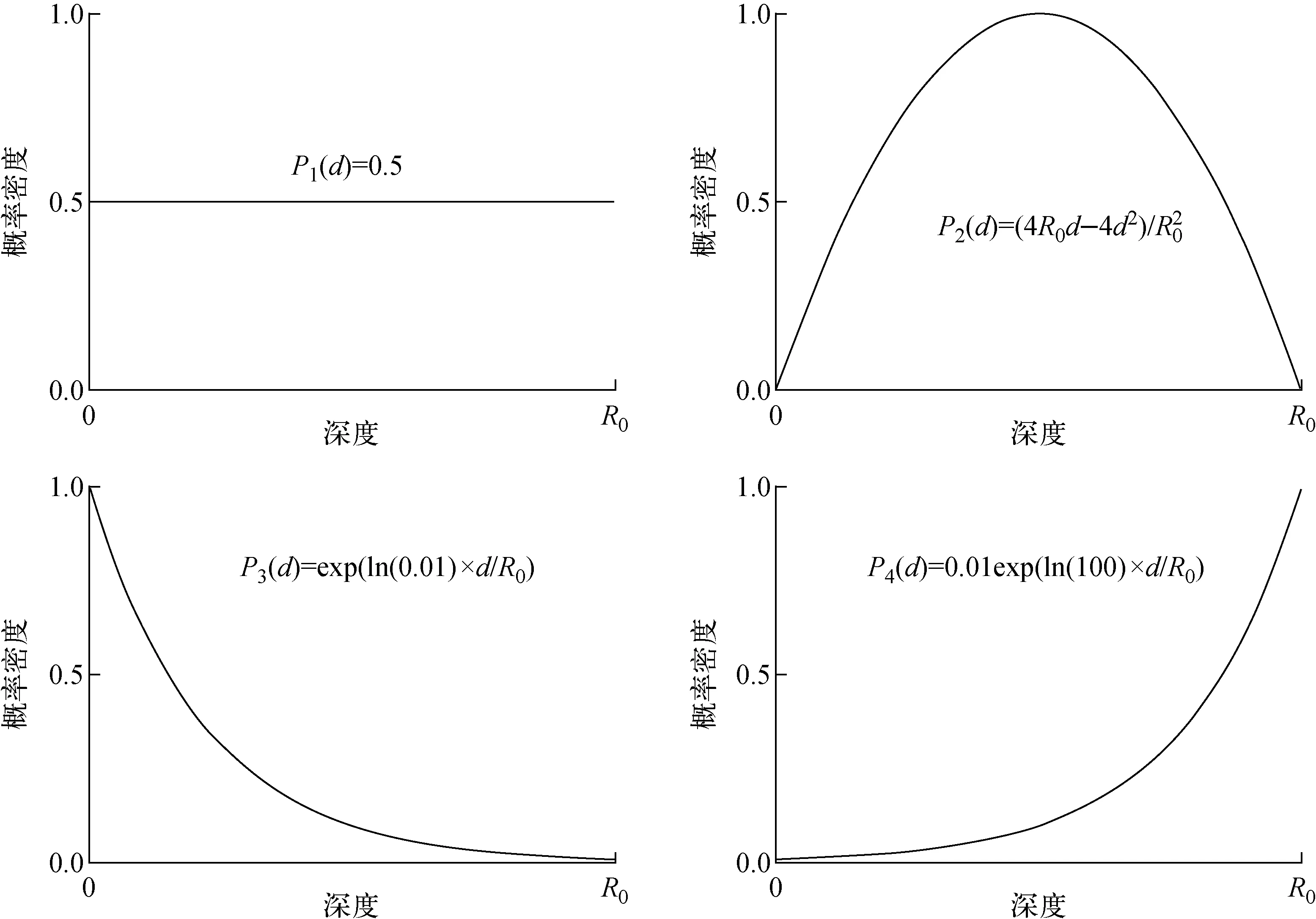
图4 均匀、二次集中型、指数递减型和指数递增型的概率密度Fig.4 Probability densities of uniform, quadratic, exponential decline and exponential increase distribution

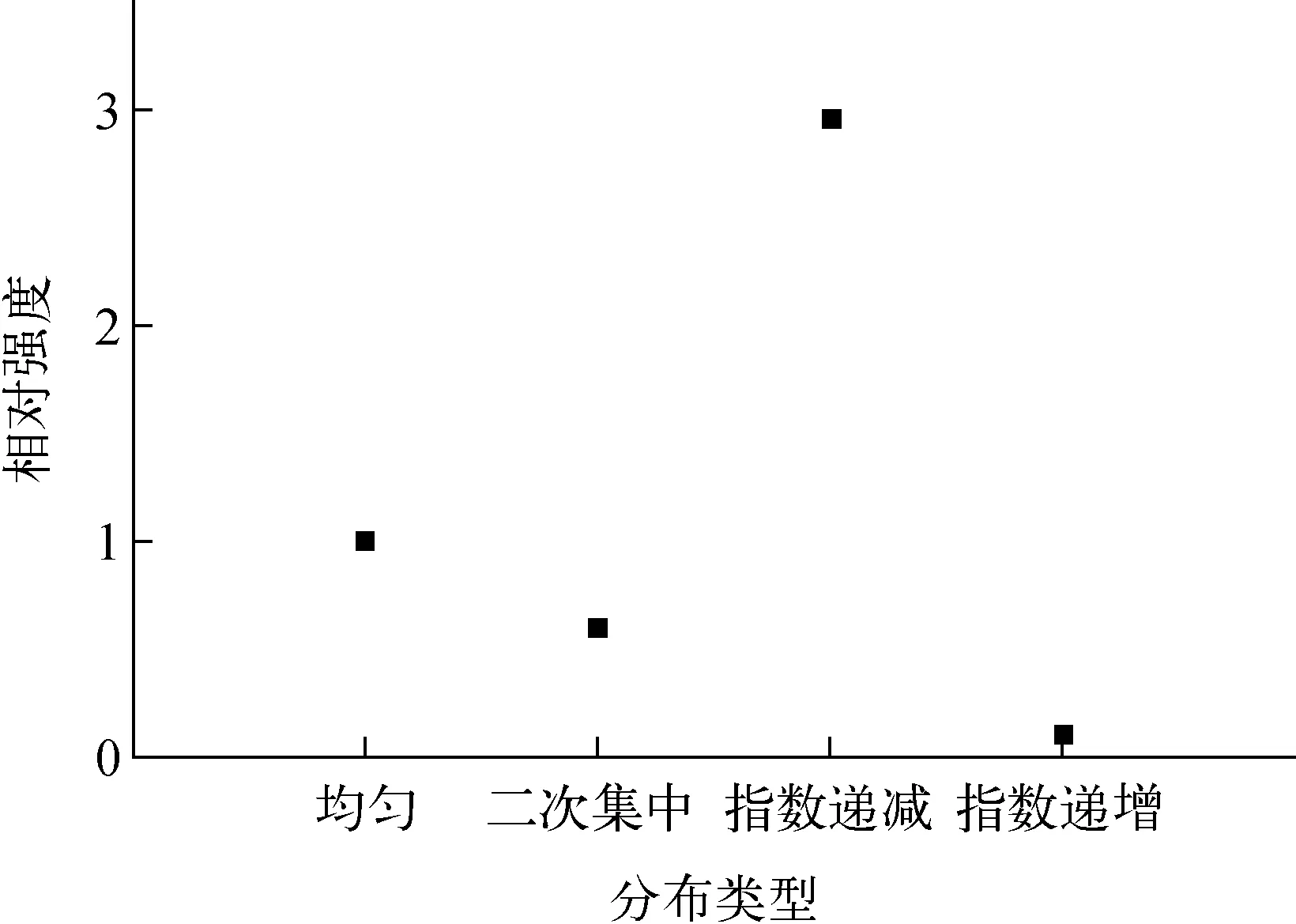
图5 316LSS样品β射线射程范围内 不同氚分布形式下的Ar(Kα)强度Fig.5 Ar(Kα) intensity of 316LSS sample in different tritium distribution forms within range of β-ray

5种材料的计算结果相近，且都显示氚在β射线射程范围内中几种分布的计算结果有明显的差异，且指数递减型和递增型之间的差异很大。在这些分布下，集中在表面的计算结果约为均匀分布的3倍，集中在中部的计算结果约为均匀分布的60%～70%，集中在底部的计算结果约为均匀分布的10%。所以如果在实验或计算过程中单纯将β射线射程范围内氚的分布看成是均匀的，可能会导致结果相差1个量级。

3 结论

通过使用MCNP5计算5种样品β射线射程范围内不同位置的Ar(Kα)强度可看出，随着深度的增加，Ar(Kα)强度呈指数衰减的规律，且越接近表面的氚对Ar(Kα)总强度的贡献越大，在表面和底部计算结果会相差300倍左右；在均匀分布氚的情况下，1/10射程内的氚贡献了约1/2的Ar(Kα)的强度。另外在β射线射程范围内，氚集中在表面、中间和底部的分布也与均匀分布得到的计算结果也有数倍的差异。也就是说在测量或计算过程中，若是将这部分的氚都按照均匀分布来考虑，则有必要对结果进行修正。