H-1NF仿星器标准磁场位形分析与高能量离子运动轨道模拟

向 东，夏彦博，宋泽宸，曹锦佳，杜 丹，管沪楠，龚学余

(1.南华大学 核科学技术学院，湖南 衡阳 421001；2.南华大学 数理学院，湖南 衡阳 421001)

仿星器和托卡马克装置是目前国际上研究最多的两大磁约束可控热核聚变装置类型。由于建造仿星器的成本高、技术难度大等诸多原因，从20世纪70年代开始，大多数核聚变研究都聚焦于托卡马克。目前中国拥有EAST、HL-2M、J-TEXT等托卡马克装置，还没有仿星器装置，因而在仿星器方面的理论研究相对较少。然而，由于仿星器内等离子体全部依靠外部磁场约束，易于实现自然稳态运行，激发大破裂的可能性非常低，这些优点在聚变界一直备受青睐[1-3]。特别是在2015年12月，目前世界上最大、设计最复杂、版本最新的德国W7-X仿星器成功实现高参数等离子体放电而轰动全球[4]。W7-X仿星器设计的远景目标是实现1 800 s超长脉冲稳态运行[5]。目前，建造中国聚变工程实验堆(CFETR)已被列为国家聚变能源发展的路线图[6]。仿星器作为未来聚变反应堆备选方案之一，其相关研究同样也受到了国内科学界的关注。西南交通大学和日本国立聚变研究所合作在中国设计筹建一个新型准轴对称仿星器CFQS[7-8]，浙江大学、中国科技大学等高校聚变研究团队也开始了关于仿星器的理论研究[9-10]。为了在国内广泛开展H-1NF仿星器的实验和理论研究，本文对H-1NF仿星器的磁场线圈组成和分布特征进行分析，研究其磁场位形特点及单粒子运动轨道特征，并模拟计算高能量离子在一种标准磁场位形中的典型运动轨道。

1 H-1NF仿星器磁场线圈分布

H-1NF仿星器的磁场沿大环方向三周期120°对称分布[11-13]，如图1所示，其磁场线圈系统共包括36饼环向场线圈(TFC)，1个中心环导体，即极向场线圈(PFC)，1条螺旋线圈(HCW)，1对内垂直场线圈(IVFC)，1对外垂直场线圈(OVFC)。其中，环向场线圈、极向场线圈、螺旋线圈和内垂直场线圈均安装在仿星器真空腔体内，外垂直场线圈安装在真空腔体外。

a——三维视图；b——俯视图图1 H-1NF仿星器磁场线圈分布Fig.1 Distribution of magnetic field coil of H-1NF stellarator

36饼环向场线圈的大小规格相等，每饼环向场线圈内部绕有10圈铜导线，其平均等效半径RTFC=0.38 m。这些环向场线圈的圆心不在同一平面上，若采用大柱坐标(R，φ，Z)来描述各线圈的分布位置，则每个环向场线圈的圆心坐标(Rc，φc，Zc)满足以下关系式：

Rc=R0+ρscos(3φc)

(1)

Zc=ρssin(3φc)

(2)

φc=φ′-0.009 7sin(3φ′)

(3)

(4)

其中：R0为大半径，R0=1.00 m；ρs为摆动半径，ρs=0.22 m。

中心极向场线圈位于Z=0.00 m的赤道面上，其内部绕有36圈铜导线，其线圈等效半径RPFC=1.00 m。1对内垂直场线圈分别对称分布于赤道平面Z=±1.07 m的平面上，每个内垂直场线圈内部绕有16圈铜导线，其线圈等效半径RIVFC=0.72 m。1对外垂直场线圈分别对称分布于赤道平面Z=±0.70 m的平面上，其内部绕有12圈(通过外部引线可设置成4、8、12圈3种，其标准配置为8圈)铜导线，其线圈等效半径ROVFC=2.13 m。螺旋线圈内部并排4条铜导线，它们沿环向呈3周期缠绕中心极向场线圈，缠绕的等效小半径rHCW=0.10 m。

H-1NF仿星器线圈标准接线方式是将环向场线圈、极向场线圈、内垂直场线圈、外垂直场线圈中的铜导线全部串联，由ABB电源的主回路供电，而螺旋线圈由ABB电源的从回路供电。通过设置ABB电源主、从两路输出的电流强度，可获得不同的磁场位形。H-1NF仿星器标准运行模式是外垂直场线圈设置为8圈铜导线，且螺旋线圈不供电。在标准运行模式下，当主路输入的铜导线电流强度为13 889 A时，若将中心极向场线圈等效看作是一圈圆电流，则其电流强度约为5.0×105A，此时磁轴上的磁感应强度约为1 T。本文以此种H-1NF仿星器标准运行模式下磁场位形为例，分析其位形特点，并模拟计算研究高能量离子在该标准磁场位形中的典型运动轨道特征。

2 标准配置下的磁场位形

H-1NF仿星器运行时，磁面将围绕中心极向场线圈沿环向呈三周期麻花状分布，令最外层磁面为等离子体边界，绘制出其等离子体位形如图2所示。基于H-1NF仿星器标准运行模式参数，采用HELIAC程序追踪计算各磁面的磁场线[13]，分别绘制出不同环向角φ=0°、15°、30°、45°、60°、75°、90°、105°、120°等真空磁场的庞加莱图，如图3所示。由图3可看出，仿星器真空磁面沿环向螺旋状分布，这与托卡马克磁面为环向对称分布有很大不同，且仿星器的磁轴不在一平面上。另外，图3a和图3i显示出φ=0°和120°磁面的极向截面完全相同，这说明H-1NF仿星器的磁场分布是沿大环方向3周期120°对称。

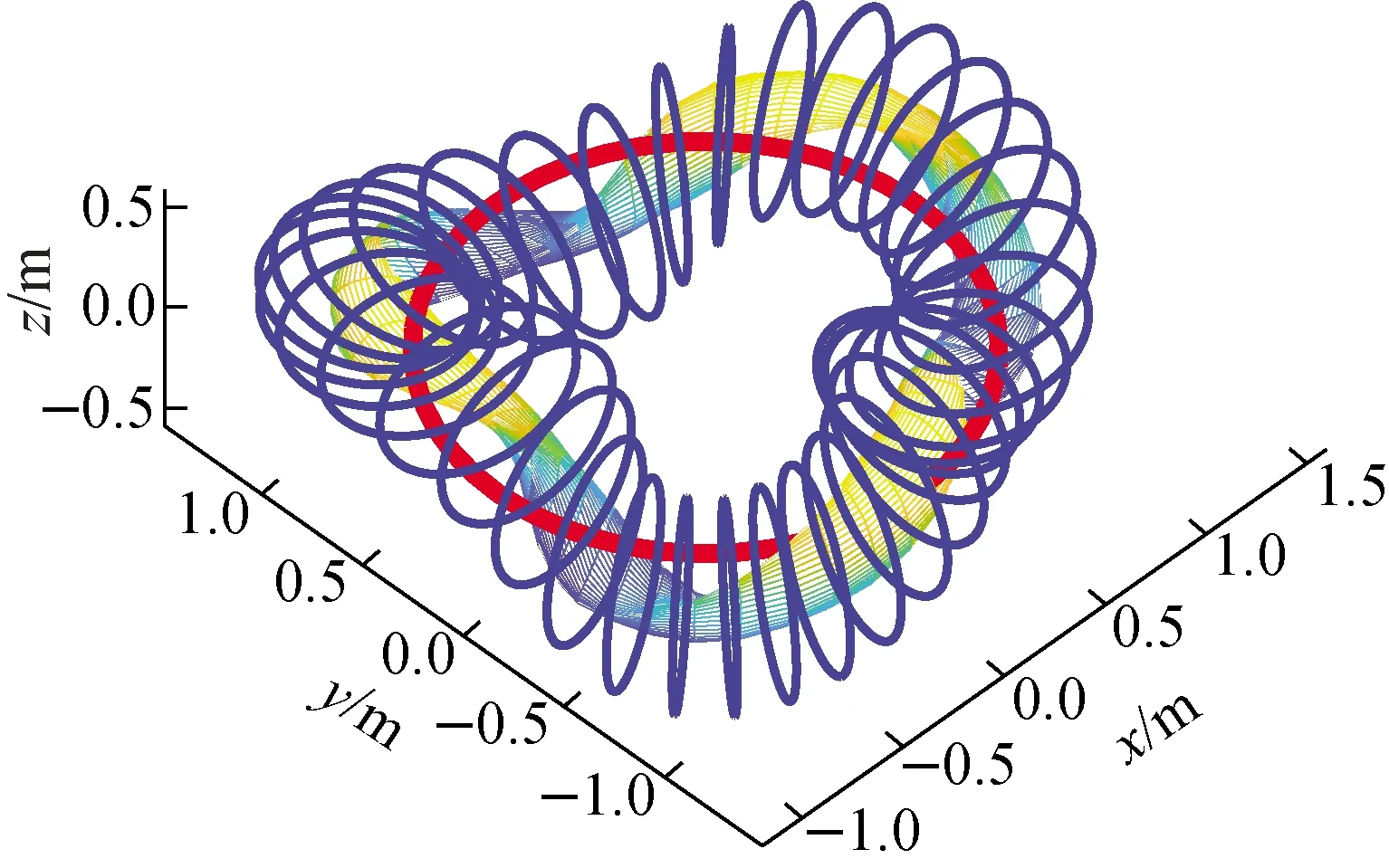
图2 H-1NF仿星器内等离子体位形Fig.2 Plasma shape in H-1NF stellarator

虽然仿星器磁面沿环向螺旋状分布不具有环向对称性，但是不同环向角的磁面极向截面除了沿磁轴旋转一定角度外，其形貌特征相近。因此，基于磁轴的位置和磁面沿环向角的变化规律，以磁轴为旋转轴，将图3所示的不同环向角的极向截面的磁场庞加莱图在原有截面坐标(R，Z)内，围绕磁轴旋转一定的角度，并将坐标原点平移至磁轴的位置，定义旋转后的极向截面坐标为(R′，Z′)，此截面称为旋转坐标系下的等效标定极向截面。因此得到了一种旋转坐标系下等效标定极向截面上的磁场庞加莱图，图3所示的各种极向截面的磁场庞加莱图经过旋转变换后对应的等效标定极向截面的磁场庞加莱图如图4所示。

在H-1NF仿星器标准运行模式下，螺旋线圈不通电，而环向场线圈、极向场线圈、内垂直场线圈和外垂直场线圈均可看作是一个等效的单匝圆形线圈导体。圆形导体产生的磁场可用第二类椭圆积分来表示，而这种积分可采用Hastings型多项式来计算[14]。因此，基于圆形导体产生磁场的计算方法和场强叠加原理，可实现H-1NF仿星器内任一点的磁感应强度计算。根据这一原理，HELIAC程序计算磁场以实现任一磁场线的追踪。本文采用此方法，利用Matlab编程计算出环向角φ=0°时极向截面的磁场分布特征(图5)。图5a为旋转坐标系下环向角φ=0°时等效标定极向截面的磁场庞加莱图；图5b为图5a中示意磁面(极向截面为一个环)随极向角变化的磁感应强度分布；图5c为旋转坐标系下Z′=0直线上沿R′方向的磁感应强度分布。

a——φ=0°；b——φ=15°；c——φ=30°；d——φ=45°；e——φ=60°； f——φ=75°；g——φ=90°；h——φ=105°；i——φ=120°图3 不同环向角的极向截面的磁场庞加莱图Fig.3 Poincaré map of magnetic field in poloidal cross-section with different toroidal angles

3 高能量离子的典型运动轨道模拟

忽略重力场等次要因素，离子在真空磁场B中的运动遵循动力学方程：

(5)

其中：m、q和v分别为离子的质量、电荷和运动速度；t为运动时间。

计算运动轨道的数值算法采用四阶龙格库塔算法[15]。另外，数值精度还与每个离散时间步Δt所对应的空间尺寸有关，因此计算前必须估算离子在计算区域内磁场中的拉莫尔半径(rL=mv⊥/qB)，以保证离子在磁场中运动1个回旋周期的数值模拟经过了足够多的时间步数演算。在磁场中运动离子的漂移速度与离子的能量、荷质比、投掷角和背景磁场均有关系。若离子的初始位置不同，其所在位置的磁场就可能不同，且在运动中由于离子位置处于不停地变化中，因此其轨道上每一点的磁场会不停地变化，投掷角也会不断地改变。对于低能量离子，其漂移速度很小，回旋运动的导心基本会沿磁力线走，因此，以下主要研究高能量离子的运动轨道特征。

a——φ=0°；b——φ=15°； c——φ=30°；d——φ=45°；e——φ=60°； f——φ=75°；g——φ=90°；h——φ=105°；i——φ=120°图4 旋转坐标系下不同环向角的等效标定极向截面的磁场庞加莱图Fig.4 Poincaré map of magnetic field in equivalent calibrated poloidal cross-section with different toroidal angles in rotating coordinate system

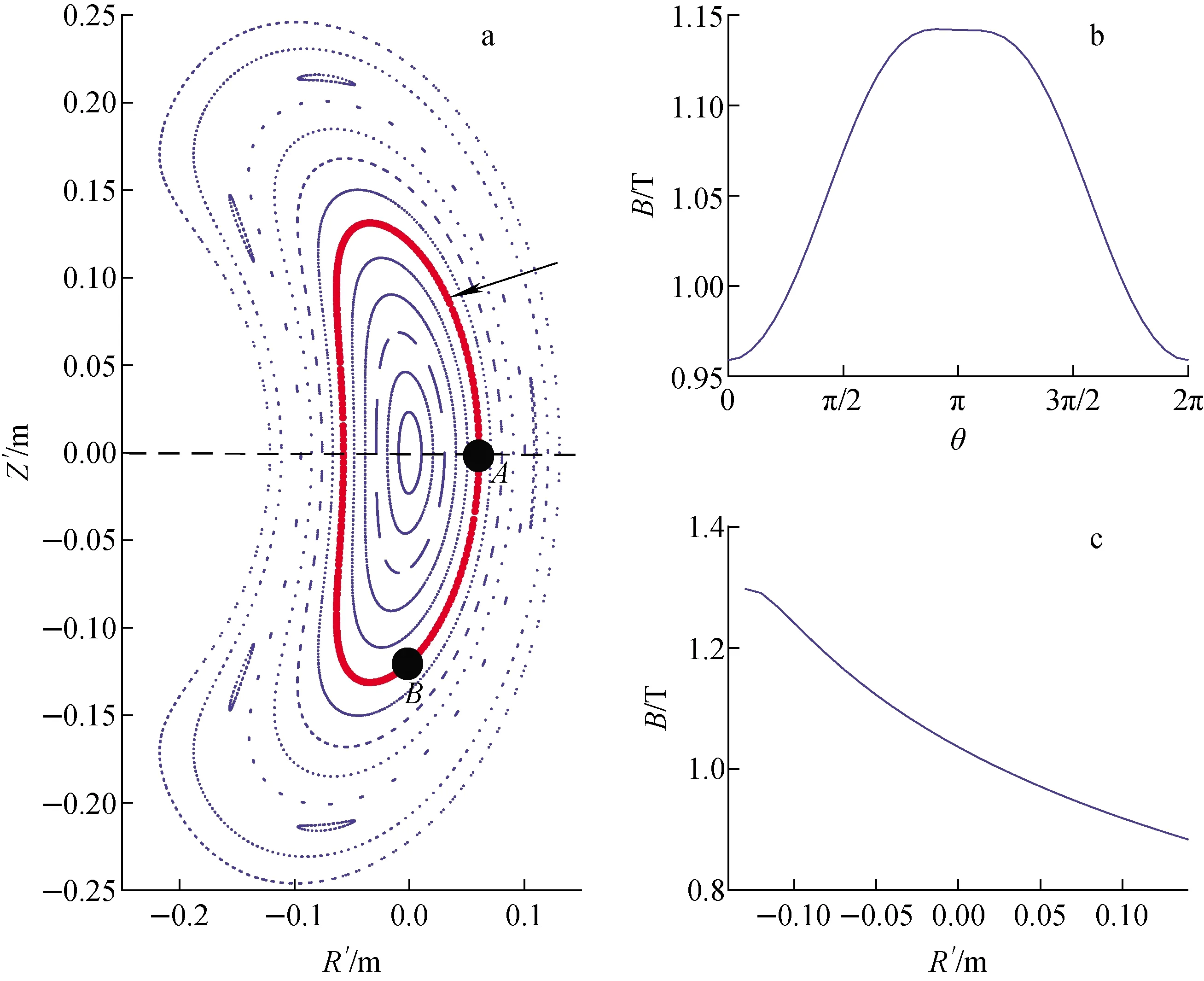
图5 环向角φ=0°时极向截面的磁场分布特征图5 Distribution characteristic of magnetic field in poloidal cross-section with toroidal angle φ=0°

不失一般性，本文令测试离子为质子，能量为10 keV，假设其初始位置的导心在环向角为φ=0°时图5a所示磁面上的点A，其极向截面坐标为(R=1.30 m，Z=0.00 m)，相应旋转坐标系中等效标定极向截面坐标为(R′=0.06 m，Z′=0.00 m)。令离子的初始投掷角为η，则cosη=v∥/v，v∥为离子速度平行磁场方向的分量。通行粒子轨道和捕获粒子轨道间的临界投掷角ηc满足：

(6)

其中：Bs为离子初始位置的磁感应强度；Bm为离子运动轨道上的最大磁感应强度。在0°～90°范围内，当离子的初始投掷角η<ηc时为通行粒子，反之为捕获粒子。根据图5b的磁场数据可初步理论估计ηc，但因为仿星器磁场分布不具有环向对称性，在不同环向角对应的旋转坐标系中标定极向截面上的磁感应强度沿极向角分布会有一定的差异，所以实际的ηc与根据图5b简单理论的估计值不同。经过精细计算，得到ηc=57°。若令离子的初始投掷角η=30°，则模拟计算出其运动全轨道如图6所示，显然这是一种典型的通行粒子轨道。若将离子的初始投掷角增加到η=60°，则可得到一种典型的捕获粒子轨道，其模拟计算出的全轨道如图7所示。

由于仿星器磁面不具有环向对称性，因而无法像研究托卡马克中的粒子轨道一样将三维粒子轨道直接投影到二维极向截面上观察。从图6、7中无法直接观察离子运动轨道相对于磁面的位置，也不能直接判断离子是否飞出最外层闭合磁面。然而，H-1NF仿星器内不同环向角的极向截面沿磁轴旋转一定角度后形貌特征相近(图4)。因此，基于磁轴位置和和磁面沿环向角的旋转变化规律，可将高能量离子的三维运动轨道投影到类似图4所示的旋转坐标系中不同环向角的等效标定极向截面上，从而可更加直观清晰地显示出高能量离子在仿星器磁场位形中的运动轨道特征。虽然旋转坐标系中不同环向角的等效标定极向磁面不完全相同(图4a～i)，但是差别不大。为了简化，统一取φ=0°的标定极向磁面作为背景，分别绘制出图6、7所示的三维粒子轨道对应在旋转坐标系中等效标定极向截面的二维轨道投影(图8、9)。从图8可看出，仿星器中的通行粒子轨道与托卡马克中的通行粒子轨道特征相似，但仿星器中的通行粒子在旋转等效标定极向截面上绕几圈后才闭合。从图9可看出，仿星器中的捕获粒子与托卡马克中的捕获粒子类似地形成了香蕉轨道，但在旋转等效标定极向截面上仿星器中香蕉轨道并未闭合，且轨道逐渐向外侧漂移，最终有可能飞出最外层闭合磁面导致粒子损失。

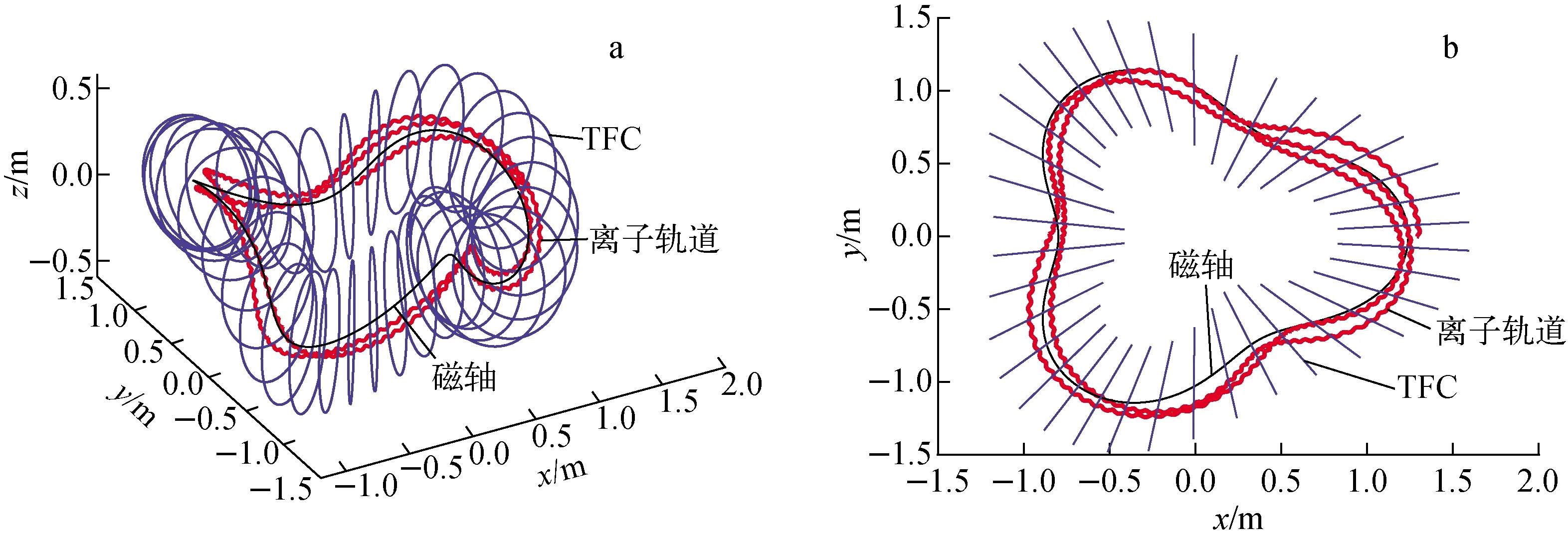
a——三维视图；b——俯视图图6 高能量通行粒子全轨道模拟图Fig.6 Full-orbit simulation of energetic passing particle

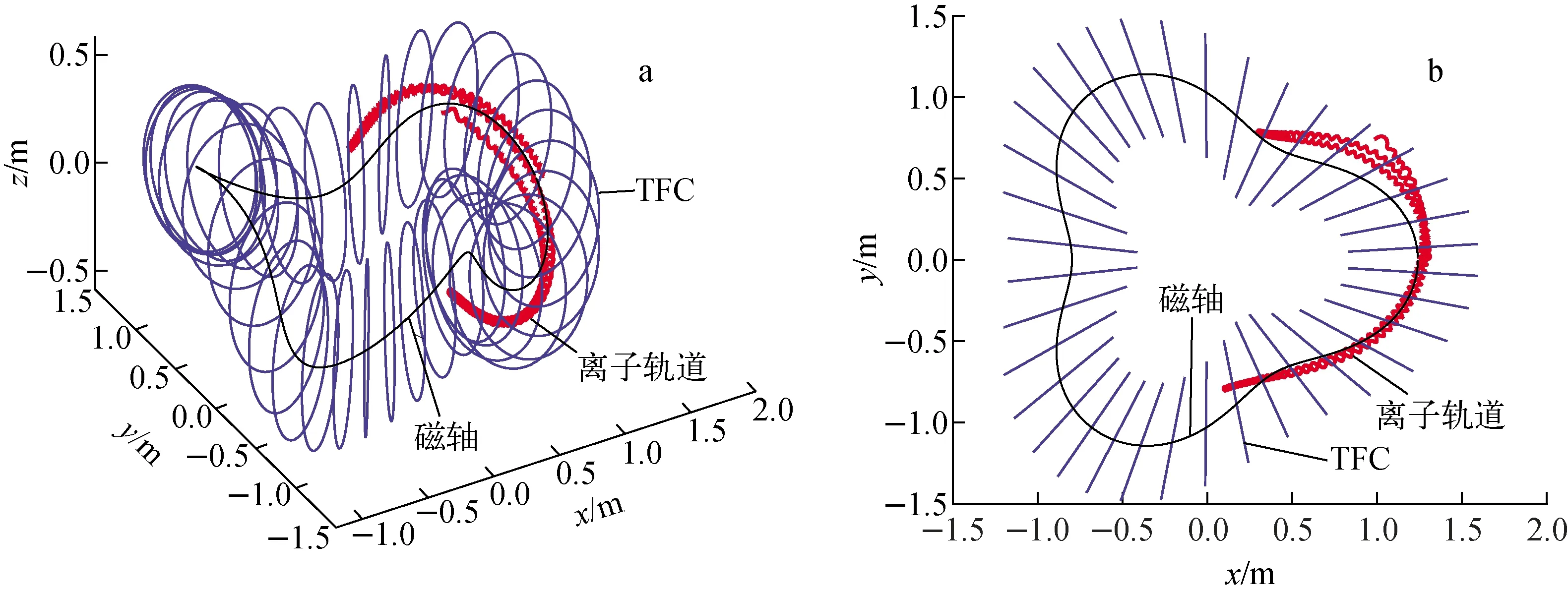
a——三维视图；b——俯视图图7 高能量捕获粒子全轨道模拟图Fig.7 Full-orbit simulation of energetic trapped particle

图8 高能量通行粒子轨道在旋转坐标系下的 等效标定极向截面上的轨道投影Fig.8 Orbit projection of energetic passing particle on equivalent calibrated poloidal cross-section in rotating coordinate system

采用上述方法对不同初始位置的测试离子进行大量试算，以进一步证明此方法的有效性。例如，设置测试离子的初始位置的导心是环向角为φ=0°时图5a所示磁面上的点B，其旋转坐标系中的标定极向截面坐标为(R′=0.00 m，Z′=-0.12 m)，初始投掷角为η=60°，则该测试离子在旋转标定极向截面的轨道投影如图10所示。虽然该测试离子的初始投掷角仍为60°，但其所在初始位置的磁感应强度变大，则其临界投掷角ηc相应变大，从而满足条件η<ηc，此时该测试离子就变为通行粒子。

图9 高能量捕获粒子轨道在旋转坐标系下的 等效标定极向截面上的轨道投影Fig.9 Orbit projection of energetic trapped particle on equivalent calibrated poloidal cross-section in rotating coordinate system

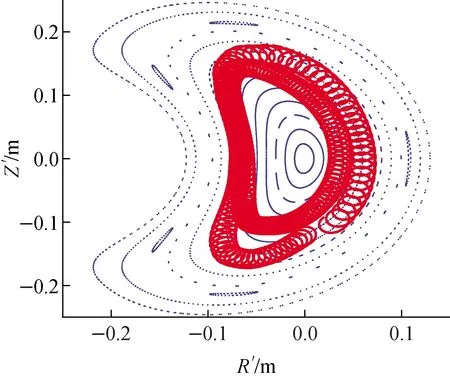
图10 高能量粒子轨道在旋转坐标系下的 等效标定极向截面上的轨道投影Fig.10 Orbit projection of energetic particle on equivalent calibrated poloidal cross-section in rotating coordinate system

4 结论

本文采用HELIAC程序计算了H-1NF仿星器在标准运行模式下不同环向角的真空磁场庞加莱图，研究其磁场位形特点，并模拟计算出高能量离子在该标准磁场位形中典型的通行粒子和捕获粒子三维运动全轨道。基于H-1NF仿星器标准磁场位形的磁轴位置和磁面沿环向角的旋转变化规律，以磁轴为旋转轴，按照旋转规律将不同环向角的极向截面旋转后得到旋转坐标系下的等效标定极向截面，并将高能量离子的三维运动轨道投影到此等效标定极向截面上，从而能更加清晰地显示出高能量离子在该磁场位形中的运动轨道特征。结果表明，H-1NF仿星器中的通行粒子轨道特征与一般托卡马克中的通行粒子轨道特征相似，不同之处是仿星器中的通行粒子轨道在等效标定极向截面上绕几圈后才闭合；H-1NF仿星器中的捕获粒子类似于一般托卡马克中的捕获粒子形成的香蕉轨道特征，但H-1NF仿星器中香蕉轨道并未闭合，且轨道逐渐向外侧漂移，最终可能导致粒子损失。

感谢澳大利亚国立大学Boyd Blackwell博士和Clive Michael博士为本工作提供的HELIAC程序代码及建议。