宇宙射线缪子核材料快速检测算法研究

钱祎剑，张立军，陈灵新，王冠鹰,*

(1.中国科学院 微电子研究所，北京 100029；2.中国科学院大学 微电子学院，北京 100190)

核材料走私威胁着世界和平发展，有效监管核材料、打击核走私一直是世界各国的关注重点。宇宙射线缪子具有穿透性强、无额外辐照等特点，相比γ射线等传统射线探测技术，能穿透Pb等屏蔽材料，不会破坏待测物质和危害人员安全，是核材料的理想检测技术。2003年，美国LANL根据缪子在物质中的库伦散射特性，提出用于核材料检测的PoCA[1](point of closest approach)算法，成功对两条钢轨和钨块进行成像。随后LANL基于极大似然估计开发了成像精度更高的MLSD(maximum likelihood scattering and displacement)[2-4]算法，主要应用于对核反应堆和核燃料存储状态的监测[5-6]。对这两类算法的改进研究[7-9]主要以高精度成像为目的，为保证成像区域有足够的缪子探测数据进行观测，需较长的探测时间，在港口、铁路等货运量大，需快速检出待测物是否为核材料的场合并不适用。近几年，为提高核材料检测速度，不通过成像来判别是否存在核材料的宇宙射线缪子快速检测算法被提出[10-13]。2019年，中国科学技术大学的何伟波用灰色关联分析[13]实现了仅用缪子散射角数据即可对U、Pb、Fe进行分类，2 min的探测时间对U和Pb的区分可达到95%以上的准确率。

为进一步提高用宇宙射线缪子检测核材料的速度，研究采用较少的缪子探测数据实现核材料检测，本文利用Geant4[14]软件仿真缪子库伦散射数据进行分析验证，研究缪子探测数据的概率分布函数和高阶统计量，使用支持向量机测试这些参数对核材料和检测干扰物的分类性能，并提出一种新的宇宙射线缪子核材料快速检测算法。

1 原理

使用宇宙射线缪子对核材料进行检测成像是根据缪子在材料中的库伦散射特性实现的。宇宙射线缪子产生于宇宙射线与地球大气的粒子反应，在地球海平面处平均通量约为10 000 min-1·m-2。缪子穿过物体时会发生能量损失和库伦散射，其中缪子在材料中多次库伦散射后偏转角度近似于零均值的高斯分布，其平面角和立体角时的分布均方根RMS(mrad)分别为式(1)[1]和式(2)[2]。

(1)

(2)

其中：βcp为缪子入射能量，MeV；x为缪子穿过物体时的路径长度；X0为物体材料的辐射长度(g·cm-2)，其定义[2]为：

(3)

其中，Z、A分别为材料的原子序数和相对原子质量。式(2)在10-3>x/X0>102时能较好描述缪子穿过材料的库伦散射角分布，其误差好于11%[15]。

式(1)～(3)表明，缪子在穿过物体时库伦散射角分布与物体材料原子序数有关。通过统计缪子探测数据，计算出穿过待测物体的缪子库伦散射角分布均方根值，即可据此判断空间内是否存在核材料。检测算法所需的缪子探测数据量越少，对应所需的探测时间就越少，核材料检测速度就越快。

2 仿真环境的建立和数据获取

为快速获取大量缪子穿过不同材料的散射数据，进一步开展宇宙射线缪子核材料快速检测算法研究，使用Geant4软件包获取缪子穿过待测材料时的库伦散射角仿真数据。Geant4仿真环境设置如下：在空气环境中以坐标原点为中心放置一块厚度10 cm、底面为100 cm×100 cm的待测材料，在待测材料中心上、下50 cm处放置3层间隔5 cm、厚度为1cm、面积为100 cm×100 cm的塑料闪烁体(材质为聚苯乙烯，密度为1.05 g/cm3，H/C比为1.12)作为缪子探测器。仿真环境如图1所示，处于上、下两组缪子探测器中间部分的1 m3立方体为探测空间。通过记录缪子穿过上、下两组探测器的位置，分别拟合入射和出射直线，计算其夹角即可得到缪子穿过探测空间时的散射角。

式(2)描述的缪子库伦散射角分布均方根包含缪子入射能量，对于不同入射能量、入射角度的缪子散射数据，忽略式(2)中较小的对数项，可将其归一化得到相同入射能量、垂直入射缪子的散射角：

(4)

其中：pin为缪子入射动量；θin为缪子入射角度；θs为缪子穿过探测空间时的累积库伦散射角。式(4)是归一化入射天然源缪子的有效方式，参照已有研究[4,13]，假设探测器的接收效率为100%，在Geant4仿真环境中，直接采用能量为3 GeV、垂直入射的缪子点源代替天然缪子源项，位于最上层探测器中心上方5 cm处，点源与探测器之间的空间为真空环境。该设置简化了天然源缪子的数据处理流程，利于快速获取不同材料中的缪子库伦散射数据，开展对缪子散射探测数据分布的研究。

图1 仿真实验环境示图Fig.1 Illustration of simulation experiment environment

选择元素U(Z=92)作为被检测的核材料，用Pb(Z=82)作为检测干扰物，另外选择生活中常见的Fe(Z=26)作为一般物。将U、Pb、Fe分别设置为上述环境中的待测材料，分别仿真获取500 000个缪子散射数据，作为不同材料的缪子库伦散射角数据集；同时在不放置待测材料时，获取相同数量的缪子散射数据作为空气的库伦散射角数据集。最终仿真得到各材料缪子库伦散射角数据集，其统计均方根列于表1，由于仿真环境的探测空间中为空气背景，实际在Geant4中测得的缪子库伦散射角为空气和待测材料共同作用的结果，不同材料的库伦散射角数据集均方根略大于式(2)计算的理论值。

3 缪子库伦散射探测数据特征分析

已知探测空间内的材料情况，则可理论推导缪子散射探测数据的统计量和概率分布函数；反之，通过缪子散射探测数据估计概率分布函数参数或计算其统计量，可反演出探测空间内的材料情况。结合机器学习分类算法，可根据这些数值对不同材料进行分类，将这类数值称为缪子散射探测数据的分布特征。分别利用缪子散射探测数据估计概率分布函数参数和高阶统计量作为分布特征进行分析，使用支持向量机(SVM)测试分布特征对不同材料分类的性能。

表1 Geant4仿真的10 cm厚度材料 缪子库伦散射角数据均方根Table 1 RMS of Geant4 simulation data for Muon Coulomb scattering angle of 10 cm thick material

3.1 基于概率分布函数参数的分布特征分析

穿过探测空间的缪子可分为两类：穿过待测物体发生了库伦散射的缪子和未穿过待测物体在空气中散射的缪子。因此探测得到的缪子散射数据的概率分布函数为高斯混合模型(GMM)，由待测物体的缪子库伦散射分布和空气中缪子库伦散射分布组合而成。探测空间内仅1种材料时，缪子散射探测数据服从2分量混合的GMM：

P(θ)=(1-ρ)G0,σair(θ)+ρG0,σobj(θ)

(5)

其中：σair为空气背景中缪子库伦散射分布均方根；σobj为穿过待测材料的缪子库伦散射分布均方根；G0，σ(θ)为高斯分布函数；ρ为混合高斯分量的占比，表示了缪子探测数据中穿过待测物体的数据占比，根据GMM的定义，有：

(6)

其中：N为探测到的缪子探测数据总量；Nobj为N个探测数据中来自待测物体的缪子数据量。待测物体体积越小，ρ越低，分辨待测物的难度就越大，如图2所示，ρ可近似用待测物体在探测器上的投影面积与探测器面积之比表示。在1 m3立方体的探测空间中，探测10 cm边长的立方体时，ρ=0.01。因此ρ可描述探测空间和待测目标之间的大小关系，以及在此条件下探测获取的缪子散射探测数据构成，同时也可作为区分不同材料时分辨率的指标。

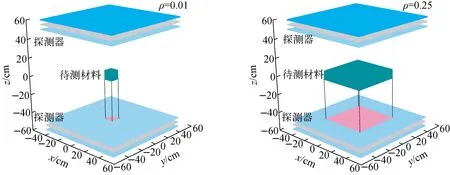
图2 探测空间和待测物体大小关系Fig.2 Size relationship of detection space and object to be measured

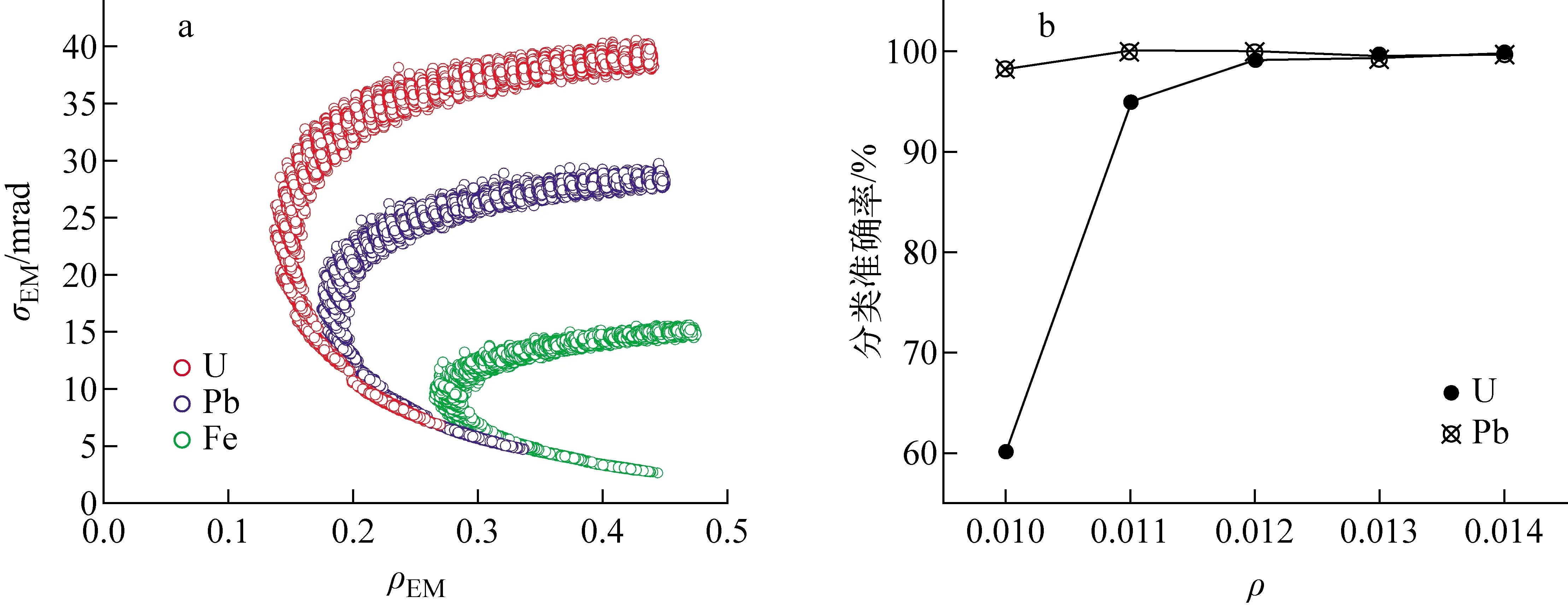
a——U、Pb、Fe的σEM和ρEM ；b——使用σEM和ρEM分类不同材料的准确率图3 使用σEM和ρEM分类不同材料Fig.3 Classification for different materials by σEM and ρEM

(7)

其中：θi为缪子探测数据；Qi为隐变量，计算式为：

Q(n)=

(8)

空气中的缪子散射分布均方根σair已知，最终σobj收敛结果即为EM算法对待测物体的缪子库伦散射分布均方根估计σEM。ρ也可由EM算法估计的σEM进一步计算隐变量得到：

(9)

由式(7)～(9)，使用EM算法可直接估计出式(5)的所有未知参数得到σEM、ρEM。根据式(6)，代入ρ和N计算出缪子散射探测数据中分别来自空气和材料的数据量，从Geant4仿真获取的不同材料库伦散射数据集抽样得到缪子仿真探测数据。取0.01≤ρ≤0.4，N=10 000的U、Pb、Fe的缪子仿真探测数据并用EM算法计算(σEM，ρEM)，如图3a所示。对于标签已知的分类问题，使用SVM对图3a中不同材料的分布特征计算分类模型并测试，结果如图3b所示。(σEM，ρEM)对Fe的分类准确率为100%；在ρ>0.01时，对U和Pb的分类准确率大于95%；而在ρ=0.01时，由图3a可见，U和Pb的(σEM，ρEM)存在较多重叠，Pb的分类准确率为98.3%时，U的准确率仅60.1%，两种材料分布特征无法区分。

为进一步分析U和Pb的(σEM，ρEM)出现重叠的原因，用Geant4仿真数据测试EM的估计效果。取0.01≤ρ≤0.4，N=10 000的U的缪子仿真探测数据计算(σEM，ρEM)并与实际值对比。如图4所示，由于(σEM，ρEM)随着ρ趋近于0收敛于(σair，0.5)，相当于无材料的情况，使得ρ<0.05时EM估计结果主要受空气中的缪子库伦散射数据影响，这与图3a中U、Pb、Fe的(σEM，ρEM)随σEM减小趋向同一方向并出现重叠一致。综上所述，使用(σEM，ρEM)作为分布特征对不同材料进行分类，在缪子散射探测数据中来自待测材料的数据占比大于1.2%(ρ≥0.012)时，对U、Pb、Fe的分类准确率可达到95%以上。但在实际检测中ρ通常会更小，对10 cm边长的立方体待测材料(ρ=0.01)，(σEM，ρEM)并不能有效区分U和Pb。

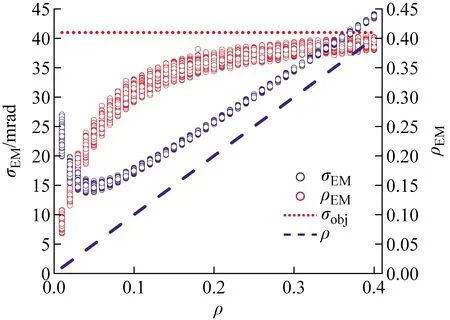
图4 U缪子探测数据σobj和ρ的EM估计Fig.4 EM estimation of U Muon detection data of σobj and ρ

3.2 基于高阶统计量的分布特征分析

上述讨论主要使用缪子散射探测数据二阶统计量对不同材料进行分类，然而二阶统计量局限于对高斯假设的分析，对非高斯数据的估计存在偏差。更高阶的统计量相比均值和方差包含有更丰富的非高斯信息[16]，其中峭度是描述数据分布峰的四阶累计量，对于零均值分布的数据，峭度计算式[17]为：

(10)

对于ρ不同的缪子散射探测数据，待测材料的缪子散射探测数据分布峰存在不同。而峭度常用于与正态分布比较数据分布峰的大小，在信号处理领域中已有广泛应用[17]，对于GMM这类非高斯分布，尝试将高阶统计量作为分布特征进行分类。为简化计算，一般用归一化的四阶矩代替式(10)计算峭度。式(5)描述了缪子散射探测数据分布的GMM，其峭度理论值KGMM可由ρ和σobj表达：

(11)

由式(11)，代入U、Pb、Fe的σobj计算KGMM取最大值时ρ为0.001 4、0.002 7和0.009 1，据此推测峭度在ρ≥0.01时其值仍主要受σobj的影响，可较好描述缪子散射探测数据分布。根据式(11)可得出ρ≥0.01时与缪子散射探测数据理论峭度KGMM的关系(取表1中U的σobj=40.98 mrad，N=10 000)，并将其与同等条件下的缪子仿真探测数据用式(10)计算的峭度值Kdata对比，如图5所示。Kdata与KGMM基本符合，但Kdata离散程度较大。由于ρ=0时数据分布为高斯分布，此时KGMM=3。但相比于σEM和ρEM，ρ较小时KGMM和Kdata均有出现明显减小，据此进一步测试ρ≥0.001时使用σEM、ρEM和Kdata作为分布特征分类不同材料的准确率。

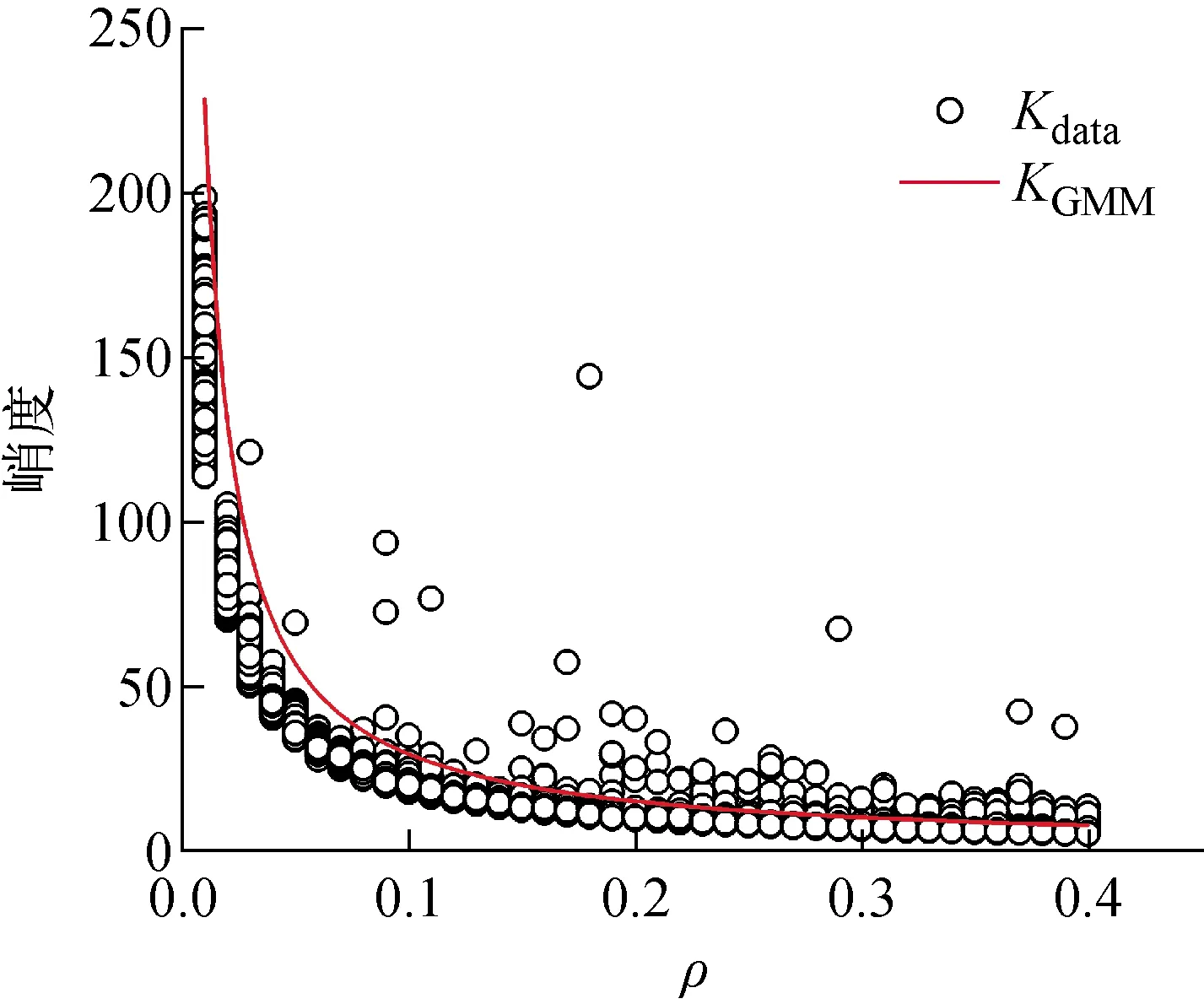
图5 ρ和2分量高斯混合模型峭度的关系Fig.5 Relationship between ρ and kurtosis of 2-component Gaussian mixture model

取0.001≤ρ≤0.4，N=10 000的U、Pb、Fe的缪子仿真探测数据并计算(σEM，ρEM，K)。如图6所示，不同材料的K在(σEM，ρEM)重叠的部分具有明显区分。同样使用SVM对U、Pb、Fe的(σEM，ρEM，K)计算分类模型并测试，结果如图7所示。在ρ≥0.01时，U、Pb、Fe的分类准确率均在99%以上，在ρ=0.001时，由于Fe作为一般物与U和Pb的缪子库伦散射能力差异较大，其分类准确率仍有96.2%，U和Pb两种相近的物质随着K收敛分类准确率下降到71.5%和71.1%，在ρ≥0.006时，3种材料的分类准确率均在95%以上。相比使用(σEM，ρEM)，增加K作为分布特征，达到相同分类准确率所需的缪子散射探测数据中来自待测材料的数据占比减小了50%。

图6 不同材料的σEM、ρEM和K分布Fig.6 σEM, ρEM and K distributions of different materials

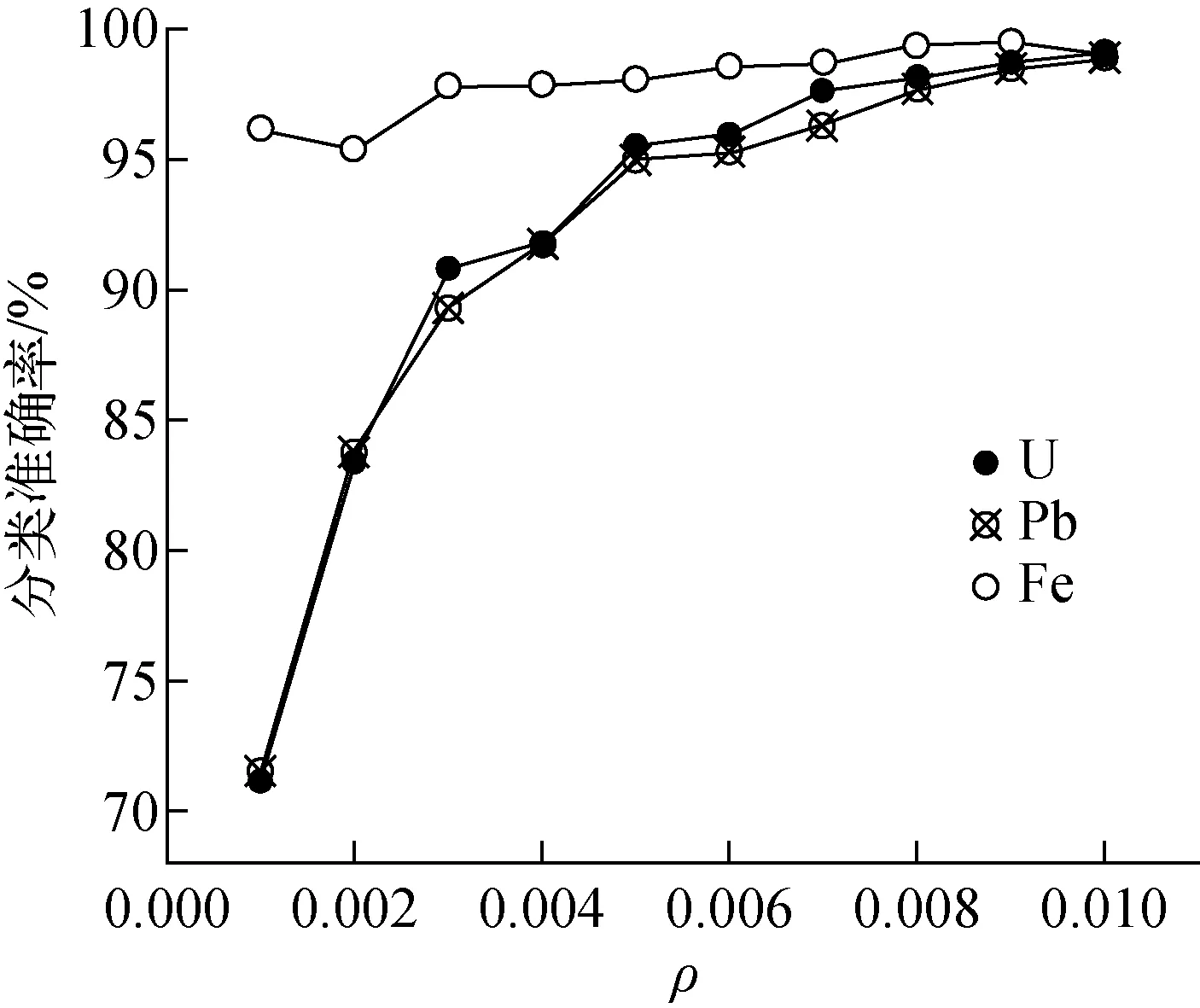
图7 使用σEM、ρEM和K分类不同材料的准确率Fig.7 Accuracy of classifying different materials using σEM, ρEM and K

综上所述，将缪子散射探测数据的概率分布函数参数和统计量作为分布特征可以对U、Pb、Fe 3种材料实现准确分类，选取的分布特征应在待测材料的缪子散射数据较少时仍能较好描述缪子散射探测数据分布的参数或统计量。前述仿真环境中设置了上下各3层的1 m×1 m的缪子探测器、探测空间为1 m3的立方体，以此构成的一个探测器单元，对于更大体积的探测空间，可用阵列的方式扩展缪子探测器的覆盖范围，数据处理时可将每个探测器单元的数据单独处理，如图8所示(图中1 GP=0.304 8 m)。由此提出基于分布特征的宇宙射线缪子核材料快速检测算法，通过Geant4仿真构建当前环境下一个探测器单元内不同材料的缪子库伦散射数据集，计算各材料缪子散射探测数据的分布特征并使用SVM计算获得材料分类模型，实现对核材料的快速检测。该算法可用N=10 000的缪子散射探测数据对100 cm2×10 cm的U、Pb、Fe进行区分，分类准确率在98.9%以上。

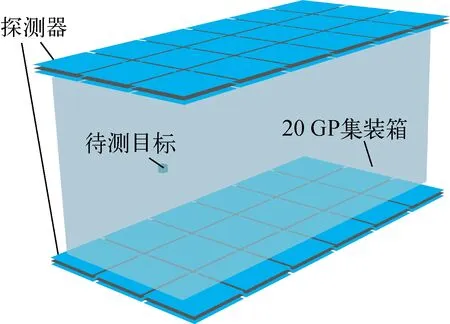
图8 用于20 GP集装箱的 宇宙射线缪子核材料探测系统Fig.8 Cosmic ray Muon nuclear material detection system used in 20 GP container

4 总结

本文分析了缪子散射探测数据的分布特征，探究了使用缪子散射探测数据的高斯混合分布模型参数和峭度对不同材料的分辨能力。为大量获取缪子仿真数据，利用Geant4仿真获取不同材料的仿真缪子库伦散射数据集，并以此提出一种快速获取缪子仿真探测数据的方法。基于上述分析和仿真数据，提出一种基于分布特征的宇宙射线缪子核材料快速检测算法，并对U、Pb、Fe的缪子仿真散射探测数据进行测试。最终用数据量为10 000的缪子散射探测数据实现对核材料(U)和检测干扰物(Pb)的区分，证明了使用缪子散射探测数据的分布特征作为材料分类依据的有效性。下一步将引入缪子入射能量和能量损失信息，进一步探究分布特征的选取方法，对多材料情况下不同厚度的材料分类进行研究，并逐步展开在现实环境下的测试实验。