橡胶支座预制浮置板轨道静动力学研究

杨文茂，周华龙，蔡文锋，刘锦辉，王 森

(1.中铁二院工程集团有限责任公司，成都 610031； 2.深圳地铁集团有限公司，深圳 518172； 3.北京交通大学，北京 100044)

近年来，轨道交通所诱发的环境振动问题不时出现[1-3]，与居民生活居住之间的矛盾愈加显著。为减小其影响，常常采用多种浮置板轨道结构[4-5]。在轨道系统设计时，轨道板强度与系统减振效果成为两大核心问题。

国内地铁在进行轨道结构设计时多参考对高速铁路无砟轨道的研究成果。张鲁顺[6]和向俊[7]分别对路基上建CRTSⅠ型板式无砟轨道结构在路基冻胀和不均匀沉降条件下的受力进行了分析。唐宇等[8]利用有限元软件建立了桥上无砟轨道静力学模型，研究桥墩沉降、梁体徐变及桥墩沉降和梁体徐变组合效应对无砟轨道线路的静力学影响。陈帅[9]和张鹏飞[10]分别针对路基和桥上CRTSⅡ型板式无砟轨道的纵向受力与变形问题进行了研究。但专门针对地铁轨道板，尤其是双向预应力预制板的研究较少。

关于浮置板轨道的减振问题，陈鹏[11]和刘克飞[12]等借助理论仿真方法，对橡胶减振垫浮置板轨道的振动传递特性进行了系统分析。赵才友[13]和王刘翀[14]分别通过现场试验表明橡胶减振垫和钢弹簧浮置板轨道的减振效果能够达到10 dB以上。杨文茂[15]通过建立车辆-轨道-隧道耦合动力学模型，对120 km/h地铁减振垫浮置板动力学特性及减振垫刚度的合理取值问题进行了研究。马蒙[16]等通过试验方法研究了钢弹簧浮置板轨道在移动列车荷载与定点锤击荷载作用下减振效果的差异。赵才友[17]等基于现场试验研究了预压质量对新型局域共振橡胶减振垫振动传递特性的影响。然而，以上研究多针对现浇浮置板道床，专门针对预制浮置板的减振性能研究尚不多见。

橡胶支座预制浮置板轨道系统是一种全新设计的点支撑式双向预应力预制板轨道。预制板受力较为复杂，需对预制板的强度进行系统检算，以保证结构安全；同时，由于预制板较现浇板更为轻质，有必要对预制浮置板系统的减振效果进行仿真，以检验其减振性能，将重点从这两个方面开展研究。

1 桥上橡胶支座预制板轨道系统

深圳市地铁6号线起自深圳北站综合交通枢纽，终于松岗站。线路全长约37.623 km，设计时速100 km[18]。全线以高架U形梁敷设方式为主，考虑到沿线环境敏感点较多，在桥上部分地段设计了橡胶支座浮置板轨道系统进行减振，其中，浮置板采用双向预应力预制板。

橡胶支座预制板轨道系统主要由钢轨、扣件、预制板、橡胶支座、钢筋混凝土基底组成。其中，预制板采用单元结构，混凝土强度等级C60，内设普通钢筋和预应力筋，板宽2 400 mm，板厚260 mm，为匹配梁长，板长设计为3 500，4 100，4 700 mm三种型式。橡胶支座采用天然橡胶材质，刚度取8～12 kN/mm，主要负责提供弹性，起到减振作用。基底采用C40钢筋混凝土结构，通过梁面预埋筋与桥梁实现牢固粘结。线下基础为U形梁，以30 m跨简支梁为主。主要结构如图1所示。

图1 U形梁上橡胶支座预制板轨道系统

2 预制板配筋检算

考虑到预制板板长分多种型式，为简化内容，以最长预制板(板长4 700 mm)为例进行分析。

2.1 设计荷载

根据Q/CR 9130—2018《铁路轨道设计规范(极限状态法)》，桥上单元结构类无砟轨道的设计作用包括列车荷载、温度梯度作用、梁体挠曲变形作用3种。

(1)列车荷载

深圳6号线采用A型车，轴重160 kN，静轮重Pj=80 kN。列车竖向荷载标准值：Pk=2Pj=160 kN；横向荷载标准值：Qk=0.8Pj=64 kN。

为计算竖向列车荷载作用弯矩，利用有限元软件建立空间实体模型，其中，钢轨、预制板、基底均采用实体单元模拟；扣件系统、橡胶支座考虑一定的宽度和长度，采用均布线性弹簧单元模拟，弹簧刚度根据扣件、橡胶支座的刚度计算得到。有限元模型如图2所示。

图2 橡胶支座预制板轨道系统空间实体模型

利用上述模型，计算得出竖向列车荷载作用下，预制板内最大纵向拉应力为3.135 MPa，最大横向拉应力为0.434 MPa。预制板内弯矩如表1所示。

表1 列车竖向作用弯矩 kN·m

横向列车荷载作用弯矩Mh=0.3Qk·h。其中，Qk为前文提到的列车横向荷载标准值，取64 kN；h为道床顶面至轨面的距离，取决于扣件组装高度、预制板上承轨台厚度等因素，本工程中h为246 mm。由此计算得出Mh=4.723 kN·m。

(2)温度梯度作用

温度梯度是指板温随板厚而出现的阶梯式递增或递减的现象，温度梯度作用效应可按式(1)计算。

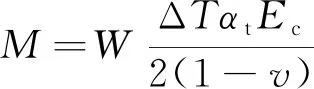
(1)

式中，W为弯曲截面系数；αt为混凝土线膨胀系数；ν为混凝土泊松比；Ec为混凝土的弹性模量；ΔT为上下表面的温差。

根据Q/CR9130—2018《铁路轨道设计规范(极限状态法)》，最大正温度梯度为90 ℃/m，最大负温度梯度为45 ℃/m，且当板厚为260 mm时，板厚修正系数取0.89，由此计算得出预制板的上下表面温差ΔT分别为20.826 ℃和10.413 ℃，相应的温度梯度作用弯矩如表2所示。

表2 温度梯度作用弯矩 kN·m

(3)梁体挠曲变形作用

根据《铁路轨道设计规范(极限状态法)》，基础变形作用效应可按式(2)计算。

M=EIκ

(2)

式中，EI为预制板抗弯刚度；κ为下部基础变形曲线的曲率。对于简支梁桥，可将桥梁挠曲形状假设为半波余弦型曲面，进而推导得出

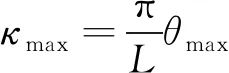
(3)

式中，L为桥跨长度；θmax为梁端转角最大值。

根据桥梁专业提供数据，深圳地铁6号线U形梁梁端转角θmax最大为1.5‰。代入式(2)、式(3)即可得出基础变形作用弯矩，如表3所示。

表3 桥梁挠曲变形作用弯矩

考虑到橡胶支座预制板轨道系统在25～35 m桥跨上均有分布，故选取最不利荷载23.854 kN·m进行检算。

2.2 荷载组合

(1)承载力极限状态下的荷载组合

在承载力极限状态下，单元结构的承载力极限状态设计应符合以下要求

γ0M≤MR

(4)

式中，γ0为结构重要性系数，对于除道岔区、伸缩调节器以外的正线轨道，γ0取1.0；MR为正截面受弯承载力；M为构件承受的弯矩组合设计值。

根据深圳地铁6号线工程特点，参照Q/CR 9130—2018《铁路轨道设计规范(极限状态法)》、Q/CR 9130—2015《铁路轨道极限状态法设计暂行规范》中的系数取值，确定弯矩M的基本组合、偶然组合分别如下。

基本组合：

M=1.5Mdk+0.5Mtdk+Mnqk

(5)

偶然组合：

M=Mdk+0.5Mtdk+Mnqk

(6)

式中，Mdk为列车荷载弯矩标准值；Mtdk为温度梯度作用弯矩标准值；Mnqk为梁体挠曲变形作用弯矩标准值。

(2)正常使用极限状态下的荷载组合

根据Q/CR9130—2018《铁路轨道设计规范(极限状态法)》，标准组合的弯矩设计值按下式确定

MQ=0.75Mdk+0.5Mtdk+Mnqk

(7)

式中，Mdk、Mtdk、Mnqk含义与前文相同。

(3)荷载组合汇总

将2.1节计算结果分别代入式(5)～式(7)，即可得出基本组合、偶然组合、标准组合的弯矩设计值，如表4所示。

表4 承载力极限状态下的弯矩组合 kN·m

2.3 配筋设计

预制板采用双向先张预应力结构，其中，混凝土强度等级为C60；预应力筋采用φ10 mm螺旋肋钢丝，其抗拉强度≥1 570 MPa，屈服强度≥1 420 MPa；普通钢筋采用HRB400级钢筋，其抗拉强度≥400 MPa，屈服强度≥360 MPa。以4 700 mm长预制板为例，预制板内钢筋汇总如表5所示。

表5 预制板钢筋汇总

2.4 预应力损失计算

以4 700 mm长预制板内的纵向预应力筋为例，进行预应力损失计算。

根据GB 50010—2010《混凝土结构设计规范》(2015年版)，先张预应力构件的预应力损失分为以下几种。

(1)锚具变形和预应力内缩引起的预应力损失为

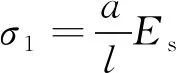
(8)

式中，Es为钢筋弹性模量；a为张拉端锚具变形和预应力内缩值，对于支承式锚具，a取1 mm；l为张拉端至锚固端之间的距离，本工况下l取4 630 mm。由此算出σ1=44.276 MPa。

(2)设备温差引起的预应力损失

设备温差引起的预应力损失为

σ2=2Δt

(9)

式中，Δt为混凝土加热养护时，预应力筋与承受拉力的设备之间的温差，本工程取35 ℃。故由此算出σ2=70 MPa。

(3)预应力筋的应力松弛

设备温差引起的应力松弛为

(10)

式中，fptk为预应力筋极限强度标准值，本工程取1 570 MPa；σcon为预应力筋的张拉控制应力，本工程预应力筋的张拉力为80 kN/根，对于直径为10 mm的预应力筋，其张拉应力为1 018.592 MPa。由此计算出σ3=18.944 MPa。

(4)混凝土收缩徐变引起预应力损失

混凝土收缩徐变引起的预应力损失为

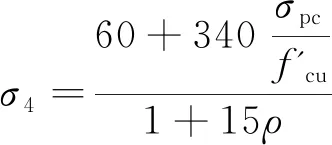
(11)

由以上计算得出预应力损失为：σl=σ1+σ2+σ3+σ4=200.288 Pa；则预应力筋有效应力σp0=σcon-σl=818.303 MPa。

2.5 承载能力极限状态检算

以4 700 mm长预制板内的纵向钢筋为例，进行承载力极限状态检算。

(1)混凝土受压区高度计算

根据GB50010—2010《混凝土结构设计规范》(2015年版)，轨道板截面受弯承载力计算图示如图3所示。

图3 轨道板截面受弯承载力计算图示

混凝土受压区高度为

(12)

(2)截面受弯承载力检算

由于受压区高度x<2a＇=107 mm，故根据GB50010—2010《混凝土结构设计规范》(2015年版)中6.2.14节要求，采用下式计算受弯承载力

(13)

其中，as、ap分别为受拉区普通钢筋、预应力筋至受拉边缘的距离。根据式(13)计算得出，截面受弯承载力M=262.418 kN·m。

采用同样的方法进行计算，得出4 700 mm长预制板内纵向、横向的截面受弯承载力如表6所示。由于预制板采用上下对称配筋，故同一截面的正、负弯矩承载力值相同。

表6 预制板截面受弯承载力汇总 kN·m

对比表4与表6可以看出，预制板纵向、横向的受弯承载力远大于弯矩的基本组合与偶然组合，表明承载力极限状态检算满足规范要求。

2.6 正常使用极限状态检算

深圳地铁6号线高架桥上轨道工程处于“干湿交替环境”，对应混凝土结构的环境类别为“二b”类，该环境类别下的预应力混凝土结构裂缝应按二级控制。即：按荷载标准组合计算时，构件受拉边缘混凝土拉应力应满足

σck-σpc≤ftk

(14)

式中，σck为荷载标准组合下的抗裂验算边缘混凝土法向应力；σpc为由预加力产生的混凝土法向应力；ftk为混凝土轴心抗拉强度标准值，对于C60混凝土取2.85 MPa。

预制板属受弯构件，荷载标准组合下的边缘混凝土法向应力为

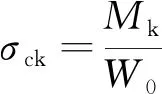
(15)

式中，Mk为按荷载标准组合计算的弯矩值。以纵向正弯矩为例，根据2.2节的计算结果，Mk=119.371 kN·m。W0为截面受拉边缘的弹性抵抗矩，根据预制板横截面尺寸，计算得到W0=0.027 m3。则可计算得出σck=4.415 MPa。

预制板采用对称配筋，由预加力产生的混凝土法向应力σpc可按下式计算

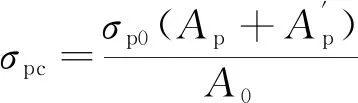
(16)

针对4 700 mm长预制板，采用同样的方法进行计算，分别得出纵向、横向截面受拉边缘混凝土拉应力如表7所示。

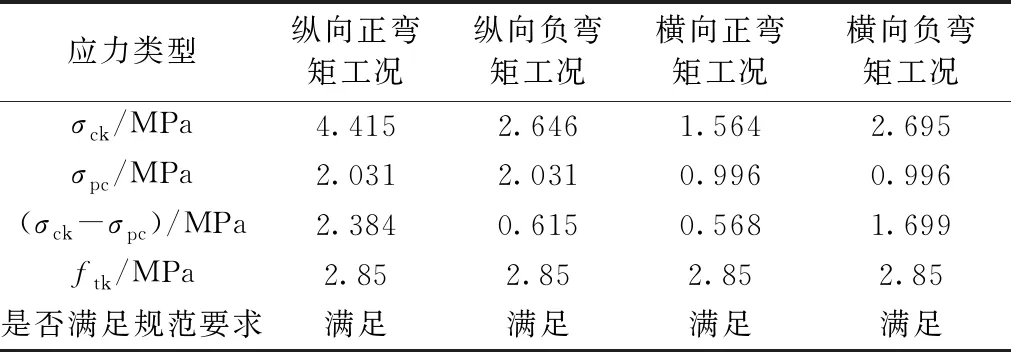
表7 预制板受拉边缘混凝土拉应力汇总

从表7可以看出，构件受拉边缘混凝土拉应力均小于C60混凝土轴心抗拉强度，表明正常使用极限状态满足规范要求。

3 系统减振效果分析

运用耦合动力学思想，建立了“车辆-轨道-桥梁”耦合系统动力分析模型，对桥上橡胶支座预制浮置板轨道系统进行动力学仿真分析。

其中，车辆模型简化为由车体、转向架以及轮对组成的多刚体系统[19]；钢轨单元在横向和垂向上均看作弹性点支承等截面梁[20]；扣件及橡胶支座采用线性弹簧模拟[21]，预制板和基底采用实体单元进行模拟，桥梁结构采用梁单元模拟[22]。根据Hertz非线性弹性接触理论[23-24]计算轮轨法向力，采用Kalker线性理论[25]求解轮轨蠕滑力。建立耦合系统模型，如图4所示。

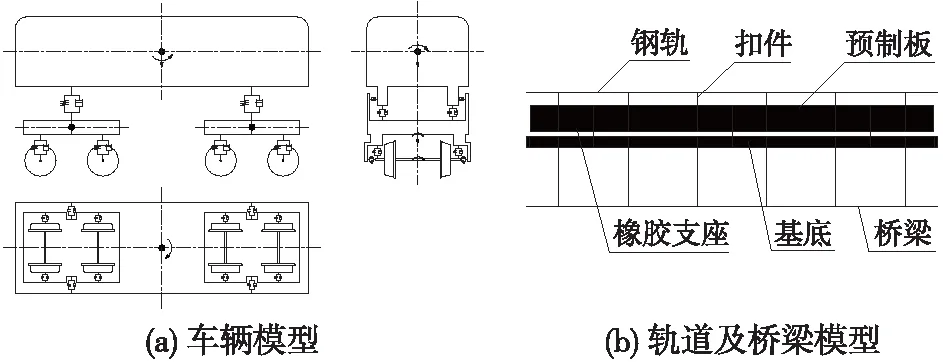
图4 “车辆-轨道-桥梁”耦合动力学模型

利用上述模型，分析了速度100 km/h条件下，橡胶支座预制板轨道系统在不同跨度U形梁上的减振效果。以30 m跨高架U形梁为例，采用普通道床与橡胶支座预制浮置板道床工况下，基底垂向加速度分频振级如图5所示。

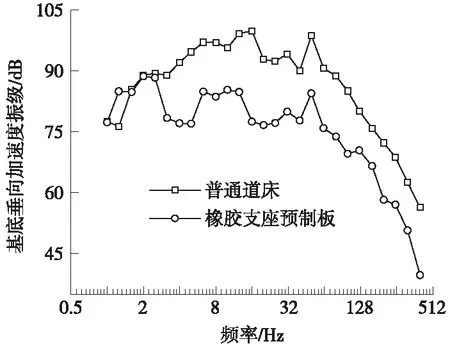
图5 普通道床与橡胶支座预制板基底加速度振级对比

根据CJJ/T 191—2012《浮置板轨道技术规范》，对25～35 m不同桥跨工况下，基底垂向加速度在1～200 Hz内的分频振级均方根值进行统计，结果如表8所示。

表8 不同桥跨工况下橡胶支座预制板系统的减振效果

从表8可以看出，不同桥跨工况下，橡胶支座预制板轨道系统的减振效果为10～13 dB。

4 结论

深圳地铁6号线首次在高架线上设计和实施了橡胶点支撑的双向预应力浮置板轨道系统。这种新型轨道结构的预应力板受力强度问题和浮置板系统的减振效果问题成为轨道结构设计中的重点和难点。通过空间实体模型及“车辆-轨道-桥梁”耦合动力学模型对上述问题进行了系统研究，结论如下。

(1)依据《铁路轨道设计规范(极限状态法)》，预制式橡胶支座浮置板轨道系统在列车荷载、温度梯度作用和梁体挠曲变形作用下，满足承载能力极限状态和正常使用极限状态设计要求。

(2)在车辆-轨道-桥梁耦合作用下，行车速度为100 km/h时，预制式橡胶支座浮置板轨道在不同跨度的高架桥梁上起到10～13 dB的减振效果，满足设计要求。

(3)配筋设计检算和减振效果分析证明了所设计的橡胶支座预制板系统能够满足深圳6号线的使用需求。所采用的“静动结合”的分析方法为后续地铁新型轨道结构的设计具有一定的借鉴意义。