广义极值分布在计算风险价值中的应用

王 震

（上海邮电设计咨询研究院有限公司，上海 200093）

0 引言

在现实世界中，对个别不常发生的事件通常称为极值事件。这些极值事件很重要，其中在金融市场，一些黑天鹅事件的发生对社会经济产生巨大的影响。对这类事件引起金融市场风险，使用风险价值（Value at Risk， VaR） 进行度量。一般计算VaR方法[1]有风险度量制（RiskMetrics）、波动率模型的经济计量模型、经验分位数以及极值理论等。该文讨论的广义极值（Generalized Extreme Value， GEV） 分布是基于极值理论的方法，该理论专门研究很少发生，然而一旦发生却产生重大影响的随机变量极端变异性的建模及统计分析方法，它提供了一种优良稳健的渐近模型对分布的尾部进行建模[2]。

该文从风险价值的概念出发，说明VaR度量方法的核心问题，讨论广义极值方法及其背后的统计理论和厚尾性质，并结合实例说明GEV估计VaR的过程、结论，进一步验证GEV具有较好的厚尾性，并通过与波动率模型的经济计量模型以及经验分位数方法的比较，说明当尾概率较小时，GEV对VaR的估计更合理的。

2 风险价值

金融市场风险包括信用风险和市场风险等[3]，VaR主要讨论市场风险。概率框架下，定义一个持有期为l、尾部概率为p的金融头寸的VaR如公式（1）所示。

式中：L（l）为金融头寸中从时刻t到时刻t+1时资产价值量变化时相关损失函数（t为时间指标）；Fl（x）为L（l）的累计分布函数（Cumulative Distribution Function， CDF）；VaR为分位数，Pr是概率函数的缩写。

公式（1）表明VaR关注的是Fl（x）损失的尾部行为。

CDF在实际应用中往往是未知的，对VaR的研究主要关心的是CDF及其分位数的估计，尤其是CDF的尾部性质[4]。因此，Fl（x）对的拟合是经济计量模型的焦点，而不同的方法估计Fl（x）产生了不同VaR的度量方法[5]。除了该文讨论的极值方法计算VaR外，还有风险度量制、波动率模型的经济计量模型以及经验分位数等。

3 计算VaR的极值方法

3.1 极值理论

极值理论研究随机变量极端值，即最大值或最小值的分布性质[5]。记某资产收益率为rt，n个收益率构成序列该序列中最小收益率记为r（1），最大收益率记为r（n）。该文以最大收益率r（n）进行理论说明， 最小收益率r（1）的情况，只需采取进行转换。

假设时间序列{rt}nt=1独立或弱相关，具有同CDF的F（x），设rt的变化范围。由概率论可知，设r（n）的CDF，记为Fn，n（x），如公式（2）所示。

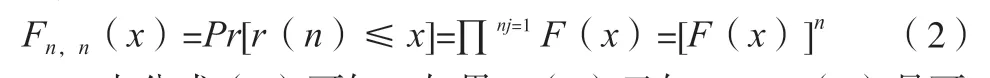
由公式（2）可知，如果F（x）已知，Fn，n（x）是可求得的，但实际中，该F（x）往往是未知的，而且最大值分布Fn，n（x）是退化[1]，这样的CDF是没有实际价值的。由 Fisher-Tippett极值类型定理[2]推得，存在2个常数列{αn}（αn＞0）和{βn}，使r（n*）≡（r（n）-βn）/αn分布当n→∞收敛到一个非退化分布，其中{αn}是尺度因子序列，{βn}是位置序列。在序列{rt}nt=1独立或弱相关的假设下，标准化的最大收益率r（n*）的极值分布函数如公式（3）所示。

式中：ξ为形状参数，exp是以e为底的指数函数。

ξ控制极值分布的尾部行为，根据ξ不同，公式（3）这种一般形式的广义极值分布可分为3种类型的极限分布[1]，当ξ=0， 为Gumbel族分布；当ξ＞0，为Fréchet族分布；当ξ＜0，为Weibull族分布。

3.2 GEV的参数估计

由式（3）及rn标准化公式知，GEV包括3个参数：形状参数ξ、尺度参数αn、位置参数βn，该文采用MLE方法[1]进行参数估计。对给定的观察样本，一般无法直接估计参数。因此将由T个收益率构成序列分成g个互不相交的子样，每个子样有n个观测值，即

将子区间内观测到的最大收益率记为rn，i，0≤i≤g，i表示第i个子区间，n表示子样大小，最后用子样最大值集合{rn，i}来估计极值分布未知参数。

设子区间最大值{rn，i}服从GEV，满足xi=（rn，i-βn）/αn的概率密度函数由式（3）求导后给出，可得rn，i的概率密度函数f（rn，i），如公式（4）所示。

式（4）中的形状参数βn有下标n表示它的估计依赖于n的大小。在rt独立性假定下，得到子区间最大似然函数如公式（5）所示。

基于公式（5），利用非线性估计程序得到3个参数估计。MLE方法估计出参数后，代入式（4）构建拟合GEV概率密度函数。为确定所拟合的模型的正确性，进行残差检验，定义残差如公式（6）所示。

在公式（6）中，代入所求的估计的形状参数、尺度参数、位置参数，求出各个rn，i的残差值wi，作残差序列图，并作{wi}对指数分布Q-Q检验图。如果GEV模型拟合正确的话，首先残差序列图中的散点不会有特定规律或趋势，其次{wi}对应指数分布Q-Q检验图中，散点应该落在45°参考直线上。通过以上检验，说明该GEV模型设定没有错误，参数拟合效果较好。

3.3 GEV计算VaR

将MLE方式估计的参数代入式（3），并再考虑式（1），得到一个空头头寸的潜在损失超过一定限制的可能性p*如公式（7）所示。

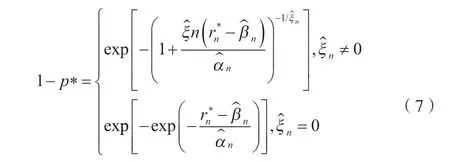
解得分位数如公式（8）所示。

式（8）的分位数是子样本最大值在极值理论基础上计算的VaR。进一步确定子区间最大值与观测值收益率序列rt的关系。由于假设时间序列是序列独立或者弱相关，由式（2）得公式（9）。

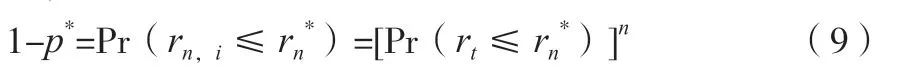
式（9）表明，概率之间的这种关系可得到原始的资产收益率序列的VaR，即对一个特定的很小的上尾概率p，且1-p=Pr（rt≤rn*），持有一个对数收益率为rt的资产，其空头头寸的VaR如公式（10）所示。

式中：n为子区间的长度。

综上，对GEV计算VaR的问题，先通过尺度参数αn和位置参数βn规范化随机变量的极值以避免极值分布退化，建立GEV分布函数。进一步，将整个序列等分成g个子区间，由各区间的极值观测值，作GEV模型的MLE参数估计，求得所拟合的GEV模型参数后，可通过式（10）求得一个特定概率p的VaR。

4 实证研究

该文选取上海某银行连续每日收盘价价格作为数据，共2694个交易日收盘价为实证分析的原始样本，设Pt（t= 1，2，…，2694）是股票在第t个交易日的价格。对长期持有股票主要考虑损失大小，因此研究最小收益问题，分别采用GEV、计量经济方法和分位数估计3种方法进行VaR估计。所有数据来源于网易财经，使用R语言对样本数据进行处理。

4.1 数据的基本统计分析

为使数据在统计上更容易进行处理[1]，该文采用股票日对数收益率，记为rt。rt= ln （Pt+1） - ln （Pt），t= 1，2，…，2693，经计算，该股票日收益率简单的统计描述，见表1。

表1可知该股票日对数收益率均值接近于0；样本标准差不大；日对数收益率的具有较高的超额峰度与偏度问题。进一步对数据进行正态性相关检验。首先构建Jarque-Bera （JB）检验统计量[1]，计算日对数收益率数据，结果JB49332，P值＜0.0001，拒绝原假设，即日对数收益率不服从正态分布。图1（a） 中，实线是该股票日对数收益率的经验密度函数，虚线是该样本均值和样本标准差决定的正态概率密度函数，两者相比，经验密度函数在均值附近有更高的峰、尾部更厚。图1（b） 中45°直线是参考线，本例来看，散点与参考线偏离程度较大，两端弯曲程度比较明显，说明该样本不服从正态分布，具有厚尾。

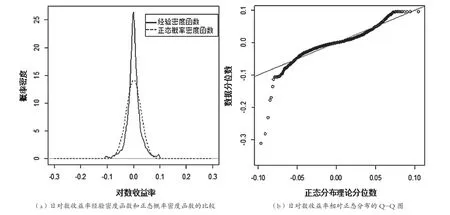
图1 上海某银行股票样本的日对数收益率的图像

表1 上海某银行股票样本日对数收益率简单统计描述

图2所示是该股票日对数收益率样本自相关函数（Autocorrelation Function， ACF），该图表明日对数收益率序列相关性很小，样本ACF值基本都在两个标准差之内，说明在5%水平下他们与0没有显著差别。进一步，该日对数收益率Ljung-Box统计量为[1]，P值分别为0.704和0.09，这说明该股票对数收益率没有显著的序列相关性。

图2 上海某银行的日对数收益率样本自相关函数图

以上检验分析指出，本例日对数收益率的样本并不服从正态分布，其分布呈现“尖峰厚尾”且数据不具有显著的序列相关性，因此该数据应用GEV计算VaR是合理的。

4.2 拟合GEV分布函数

根据式（3）的形式，建立GEV模型。利用MLE法估计GEV模型的参数，对不同的子样区间，取值不同的n得下表2。

由表2的计算结果，当10≤n≤63，形状参数ξn的估计是稳定的，近似等于0.4，但当n为126时（n为每个子样观测值的个数），由于子区间被分割为仅22个互不相交的子样，其结果具有高度可变性，估计值不稳定。由形状参数可知，该股票日对数收益率的分布属于Fréchet族。

表2 上海某银行股票样本的最小日对数收益率极值分布的最大似然估计

子周期长度选取21个交易日，由式（3）建立极值分布函数，并采用式（6）的定义，计算拟合GEV分布的残差，即负的日对数收益率拟合GEV分布时残差。作该残差图（图3），左图为残差序列图，右图为对指数分布的Q-Q图，其中，残差序列图没有显示出模型误设的问题，同时，对指数分布的Q-Q图基本在理论指数分位数的直线上，因此认为GEV分布拟合是合理的。

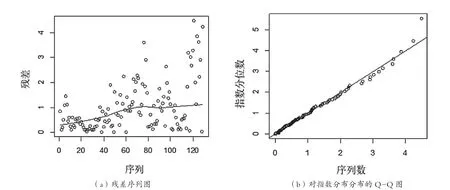
图3 上海某银行股票样本的负的日对数收益率拟合GEV分布时的残差图

4.3 计算VaR

将4.2节的参数估计结果代入式（10），计算不同置信水平下的该VaR值，见表3。

由表3表示，GEV中VaR的值对子区间长度n的选取较敏感且不同置信水平下的结果差异很大，应考虑选择对应GEV分布拟合较好的子区间长度。

表3 用广义极值分布（GEV）计算VaR结果

为进一步分析，选取子区间长度n=21的结果下，假设持有一个1000万人民币的多头头寸，考虑运用GEV、计量经济方法和分位数估计3种方法计算样本数据的VaR，求得在下一个交易日中的损失。VaR概率分别取为5%、1%、0.1%，即损失将以概率95%、99%、99.9%低于或等于VaR，各种方式计算的结果如表4。

表4看出，不同的方法结果有区别。首先，高斯AR（2）-GARCH（1，1） 模型在各VaR概率下均低估了损失，这主要是因为上海某银行股票日对数收益率的分布具有厚尾性，所以基于正态分布假设的计算VaR不是很合理。然后，对经验分位数估计VaR时，5%和1%的经验分位数的估计结果可以当作真实VaR的一个保守估计（下界），但当尾部概率很小（例0.01%） 时，经验分位数是真实分位数的一个不太合理的估计[1]。再比较自由度为3的标准化学生t-分布AR（2）-GARCH（1，1） 模型计算结果，对VaR概率5%估计较为合理，但概率较小时，会出现低估损失的问题。最后，在GEV计算VaR值时，当尾部概率较大时（例如5%），GEV方法出现低估的情况，但随着尾部概率的减小，特别是到0.01%时，估计结果都大大高于正态分布假定下的VaR，这主要是因为，当VaR概率较小时，GEV分布的厚尾性发挥作用，估计结果更合理。

表4 各方法计算持有1千万人民币的多头头寸时下一个交易日各概率VaR结果 （单位：元）

5 结语

由于极值事件在社会经济中有很重要的影响，风险价值（VaR）评估受到越来越多的关注。在金融市场风险管理中，VaR确定的关键在于其损失函数累积分布函数的确定。基于极值理论的广义极值（GEV）分布方法，通过构建非退化的最大或最小值统计量，建立综合模型研究极值分布情况，再通过转换得到一定p值的分位数，那就是所求VaR。

在实例分析时，实际收益率呈现“尖峰厚尾”，所以运用基于正态分布的模型在估计VaR存在不合理性。相比之下，GEV方法能很好刻画出极值数据分布的厚尾性，特别是Fréchet族分布形式。另外，当VaR尾概率p减小时，GEV方法能更好发挥出厚尾作用，所得VaR估计更精准合理。