面向高校 的共享单车存量调度系统设计

顾偲雯 谢陈佑 王加安 句爱松

（1.常州工学院光电工程学院，江苏 常州 213032；2.大连理工大学化工学院，辽宁 大连 116024）

共享单车具有低碳环保、占用公共资源较少等优点[1]。但由于气候、节假日等原因导致某些租赁点的单车数量出现大幅度波动，“借车难”和“还车难”问题逐渐凸显。而有的地方会因“退潮”现象而在个别租赁点遗留过多的共享单车，导致出现路面堆积、秩序混乱等不良现象[2]。甚至在多次使用后，共享单车也会出现损耗，这就需要后期的保养和补充。上述问题给企业增加了不必要的调度和维护费用[3]。在该背景下，通过调度共享单车的方式来维持供需平衡，降低共享单车企业的调运成本，提高调运效率，具有非常好的现实意义。

该文通过调查分析所在学校周围多个租赁点的实时数据，解决周边的车量调度问题。针对节假日或其他缘故造成的学校门口每到夜晚共享单车堆积过多、而学校周围其他场所的车辆数量严重不足的问题，建立多周期、多阶段线性规划模型，以共享单车企业的调度成本最小化为目标函数，科学、合理地对各个租赁点的车辆进行规划。

1 确定数据结构

该文采用稳态不含时间窗的调度模型[4]，同时为了科学、合理地考虑共享单车的数量，特地连续5 d在特定的时间点前往学校附近的7个共享单车租赁点，对共享单车的数量进行统计，并清点学校附近7个租赁点的租赁桩，得出每个租赁点的需求量，见表1、表2。通过人工观察，计算出东一门和东二门等租赁点需要调度的共享单车的数量，见表3。为方便下文介绍对学校附近的7个租赁点进行标识记号，见表4。

表2 租赁点单车需求量表（单位：辆）

表3 租赁点单车的调度量（单位：辆）

由表1～表4可以看出，在学校附近的几个租赁点中，只有东一门和东二门的租赁点在第二天早高峰来临前，共享单车的数量是有剩余的，而北站、地铁口1、地铁口2、新桥大街和四院的租赁点都是处于缺车的状态，因此，就需要在第二天的早高峰到来之际，完成对这7个租赁点的调度工作。在该背景下，确定了调度路线，以得到一个合理的调运量和需求量，有利于更好地贴近生活，使该文的研究具有现实意义。

表1 租赁点单车数表（单位：辆）

表4 标识表

2 共享单车存量调度方法论

2.1 问题描述

针对共享单车调度问题，研究人员首先将目光聚集于调度总距离，从共享单车系统需求和调度路径入手进行优化分析[5-6]。随后，考虑单车调度的静态操作模式，最小化单车节点的最终库存量[7-8]。基于此，建立单车静态平衡问题的模型，研究关于最小化不平衡状态下站点的运营成本和等待时间[9-10]。并通过Benders分解算法求解规模较大的调度模型，得到最优调度路径。相比于采用智能算法求解模型，多个投放点所需要的单车数量相互影响，导致调度路径不一致、整体调度分布不均匀，甚至会造成调度过程中出现严重的不合理现象，这种复杂情况急剧增加了共享单车存量调度问题的难度。

在学校附近通常有多个共享单车的租赁点，大多数学生出行购物、聚餐或者去乘坐地铁都会选择方便、价格便宜的共享单车。但往往到 22：00左右，由于在外的学生都要回到学校，因此会导致学校东一门、东二门的2个租赁点的共享单车数量剧增，而在新桥大街、四院、北站以及地铁口的共享单车骤减。学校附近的7个租赁点如图1所示。

图1 共享单车区域调度图

因为要在第二天早高峰前保证市民的正常生活秩序，所以一定要在22:00到第二天6:00前完成调度工作，并且要保证东一门、东二门2个租赁点的存量单车能够满足学生一天的骑行量。从公司运营角度出发，在系统调度费用最少的情况下，该文获取了最优调度方案，从而解决共享单车存量调度问题。

2.2 模型建立

该文研究共享单车存量调度问题，即研究在系统调度成本最少情况下，调度人员驾驶调度卡车对需要调度的租赁点进行调度选择时的最优路径问题，由此建立线性规划模型。同时，该文合理简化学校调度情况，将供需平衡的运输问题嵌入原单一共享单车调度问题中。

该文面对较复杂的运输系统调度问题，建立以下2个启发式规则。要求在满足这2条调度运输原则的条件下建立一个综合调度运输方案的数学模型，并且要给出共享单车从被调运点到调运点之间的具体的调度安排。

规则1： 调运的总费用最低。

规则2： 各个租赁点的共享单车的数量满足第二天的使用需求。

基于此，建立模型，如公式（1）所示。

式中：f为调运的总费用；q为共享单车单量每千米运输费用；x为共享单车的调运量；S和D均为需要调运出去的车的数量，分别面向标识A和B地；k为标识A地到标识B地的路程；i和j分别表示租赁点间共享单车的调来和运走，i∈m，j∈n。

假设有若干辆卡车参与调度，并且卡车的容量足够大，能够满足共享单车的日常调用需求。需要调出租赁点的单车数量要满足需要调入车辆的租赁点的需求，同时也要保证调出共享单车的租赁点所剩单车能够满足第二天的正常使用。

上文已经系统地对学校附近的7个租赁点每天的供应量和需求量进行数据分析，更加贴近于生活。通过数据分析可知，东一门与东二门在每天22:00到第二天的06:00分别多出68辆、75辆共享单车，而北站、地铁口1、地铁口2、四院以及新桥大街在每天22:00到第二天的06:00分别缺少30辆、33辆、16辆、17辆和47辆共享单车。现负责调度的卡车司机将要在每天22:00到第二天的06:00将东一门和东二门的共享单车分别调往北站、地铁口1、地铁口2、四院和新桥大街。并要满足这7个租赁点第二天的供应需求，同时也要将调运费用降为最低。

共享单车在调度时是用卡车进行调用的，因此，在调度的过程中会产生一些费用。该文列举了3种费用，分别是人工工资、汽车保养以及油费。为了便于更好地计算，现通过大数据、互联网和科技论文对调度费用进行经济系数化处理，形成单辆车每公里的费用。这样可以更好地分析共享单车存量调度时所产生的费用，方便求解数学建模。租赁点之间的费用列举见表5。

表5 费用表

3 结果与讨论

该文在MATLAB中构建了线性规划模型且通过linprog函数求解该模型，采用GUI模块建立共享单车调度人机界面。所涉及的程序均运行于Intel Core 3.6 GHz CPU、4 GB内存的计算机上。计算结果见表6。

表6 计算结果数据表

由MATLAB对数据进行分析处理以后，可以从数据中看出，从东一门分别向地铁口1、新桥大街调运21辆、47辆共享单车；从东二门分别向北站、地铁口1、地铁口2和四院调运30辆、12辆、16辆和17辆共享单车。由此，该文采用的调度方法所需要的最低调运成本为373元。

该方法是在7个租赁点的共享单车数量保持不变的前提下，为保证调度费用最小而求解出最优路径的方法，可是在现实生活中肯定会存在不同的情况，因此，下文针对生活中不同的共享单车数量情况对调度路径进行优化。

首先，对第一种情况进行优化。假设由于十一假期的到来，由调度中心分别向学校附近的东一门和东二门调运20辆和10辆共享单车，以供学生使用；而为了缓解地铁口1、地铁口2、北站和新桥大街假期内的出行需求，每个租赁点分别最多可以增加10辆、10辆、10辆和20辆共享单车。影响车辆增加数量的原因是租赁点的租赁桩是有限的，不可随意改动。由此该文对该优化方案进行数学建模和最优求解。建立模型如公式（2）所示。

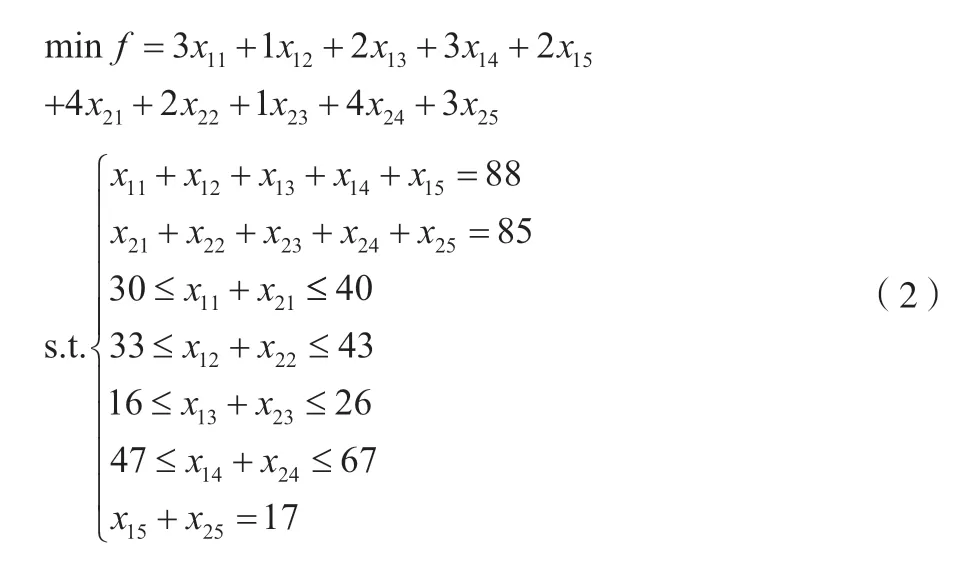
根据优化处理后得出调度数据，见表7。

表7 计算结果数据表

通过上述最优解可知，从东一门分别向地铁口1、新桥大街运送41辆、47辆共享单车，从东二门分别向北站、地铁口1、地铁口2和四院调运40辆、2辆、26辆和17辆共享单车。由此，该文采用的调度方法所需要的最低调运成本为423元。

但是经常会出现一些特殊情况，例如东一门和东二门的共享单车因为使用频次较高，所以就会导致共享单车的损坏，从而影响其他租赁点的共享单车的租用情况。在该背景下，从实际情况出发，因为四院租赁点靠近第四人民医院，一定要保证四院租赁点的共享单车数量不能减少，可以适度地减少地铁口、北站和新桥大街这几个租赁点共享单车的数量，但是又考虑到新桥大街的人流量比较大，因此北站、地铁口1和地铁口2最多可以减少10辆共享单车，一定要保证新桥大街租赁点的共享单车的数量不少于30辆。

对东一门和东二门的共享单车损坏情况进行假设，假设东一门和东二门租赁点分别损坏了20辆和10辆共享单车，针对这种优化情况进行建模求解，如公式（3）所示。

得出的调度数据，见表8。

表8 计算结果数据表

通过MATLAB的求解可以得出，从东一门分别向北站、地铁口1和四院调运1辆、30辆和17辆共享单车；从东二门分别向北站、地铁口2和新桥大街调运19辆、16辆和30辆共享单车。由此，该文采用的调度方法所需要的最低调运成本为279元。

为了简化操作以及提高系统的商用价值，该文采 用GUI模块制作共享单车调度人机界面，如图2所示，调度人员可以更直观地了解调度方案，提高了调度效率。

图2 共享单车调度GUI页面

4 结论

提高共享单车调度效率是企业提高收益的重要因素，然而调度所带来的单车投放量间的强耦合性会导致出现“借车难”和“还车难”的问题，同时调用费用可能会偏高。基于此，该文开展面向高校的共享单车存量调度研究。首先，对所在学校周围的多个租赁点进行实时数据调查分析，结果表明由于节假日或其他不确定性因素导致学校门口夜晚共享单车堆积过多，而学校周围的其他场所（例如地铁口、第四人民医院等其他场所）的共享单车数量严重不足。其次，基于上述分析建立以系统调度成本最少为目标函数的线性规划模型，对22：00～6：00各个租赁点的车辆进行合理规划。计算结果表明，该调度方法既能满足第二天的正常使用，又能提高共享单车企业的收益。此外，还可以将该方法运用到更多城市，从经济性角度解决面向政府、社会和企业的调度问题。