具有Robin自由边界的坏死核双曲型肿瘤生长模型的定性分析*

胡蝶，卫雪梅，冯兆永，刘成霞

1. 广东工业大学数学与统计学院，广东广州 510520

2. 中山大学数学学院，广东广州 510275

3. 南方医科大学口腔医院，广东广州 510280

本文研究了具有坏死核肿瘤生长模型的Robin 自由边界问题。在文献［1-2］中，Byrne 和Chaplain 提出的关于肿瘤生长的自由边界问题已被广泛研究。肿瘤生长的偏微分模型主要分三类：一是只含反应扩散方程的Byrne-Chaplain 型肿瘤模型，二是含有反应扩散方程和守恒律方程的King-Ward 型肿瘤模型，三是含有反应扩散方程、守恒律方程和Stokes方程的流体型肿瘤模型（由Franks等提出）。崔尚斌［3］介绍了肿瘤生长自由边界问题的研究内容和进展状况。在文献［4-13］中讨论了肿瘤生长细胞在Dirichlet边界条件下解的适定性和解的性质，其中文献［12-13］讨论了带有坏死核的肿瘤生长细胞在Dirichlet 边界条件下解的适定性。

2015年，文献［14］讨论了带有Robin边界条件的Byrne-Chaplain 型肿瘤生长模型的自由边界问题，得到了解的适定性和解的渐近性态。关于Robin 自由边界问题的定性分析在文献［15-20］已获得了相应的结果，其中文献［18-20］中研究了带有坏死核的肿瘤生长细胞在Robin边界条件下的定性分析。

事实上，肿瘤生长主要包括两个阶段。假设CD（正常数）表示坏死阈值：当C＞CD时，营养足够使肿瘤存活；当0 ≤C≤CD时，营养不足以使肿瘤细胞存活，所有细胞将死亡［2］。本文在文献［6］的基础上考虑营养物浓度C带坏死核的线性椭圆方程的Robin自由边界问题。具体模型如下

其中|x|≤R(t)(x∈R3)表示肿瘤在时刻t所占的空间区域（即肿瘤呈球状且R(t)为时刻t的肿瘤半径）。ρ(t)为时刻t的肿瘤坏死核半径，H( ⋅)为Heaviside 函数，P，Q和D分别代表增殖细胞、休眠细胞和死亡细胞的密度，N（正常数）代表这三类细胞混合体的密度，v代表肿瘤细胞的运动速度，KˉB(C)，KˉP(C)，KˉQ(C)分别表示增殖细胞的繁殖速率，休眠细胞变为增殖细胞的转换速率和增殖细胞变为休眠细胞的转换速率，KˉA(C)和KˉD(C)分别表示增殖细胞和休眠细胞的死亡速率，KR是与C无关的正常数，表示死亡细胞的消解速率，其中KˉB(C)，KˉQ(C)随着C的增大而增大，KˉA(C)，KˉP(C)，KˉD(C)随着C的增大而减小。另外，由于增殖率大于凋亡率，所以KˉB(C)＞KˉA(C).θ为肿瘤表面的压力即表面张力，κ表示肿瘤表面的平均曲率，C0，P0，Q0，D0，R0为初始值。

其中Ki(c)=Kˉi(Cˉc)，(i=A，B，D，P，Q).

本文的主要结果如下：

定理1 当0 ≤r≤R(t)，0 ≤t＜∞时，方程组（2）～（11）有唯一解，并且具有以下性质

1 解的存在唯一性

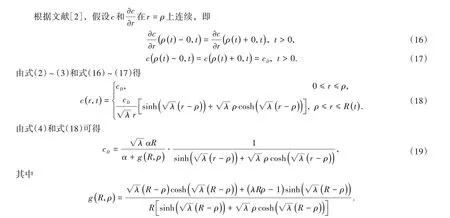
由式（19）得

若R＞R*，方程（23）的解为

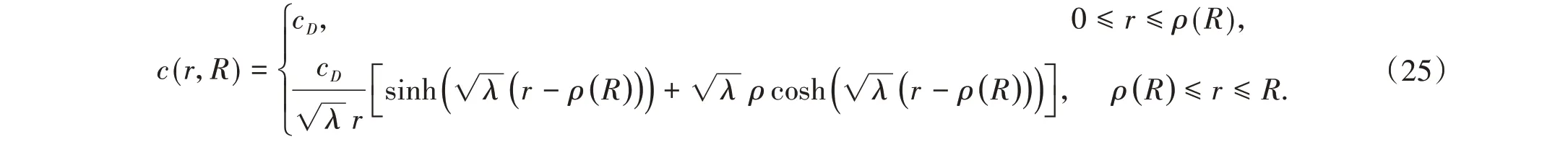
2 转换方程组

为了能够更简便地求解以上方程组，我们将其转换为一个与之等价的固定区域进行求解。作变量替换

证明σ(z，R)关于z和R的单调性可由求导直接得出。利用L'Hospital 法则易知式（40）成立，再由式（21）知式（41）显然成立。由式（19）和式（27）可知，0 ≤z＜1时，

3 等价方程组局部解的存在唯一性

我们先作出如下假设：

显然XT是一个完备的度量空间。

定义映射F：XT→XT的具体形式如下

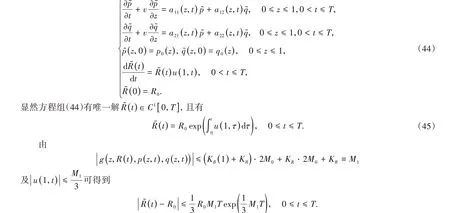
因此，当T足够小时R͂(t)满足式（43），即R͂(t)满足条件（i）。

由文献［11］中的引理4.2和引理4.3得，当T足够小时有∞

因此，p͂(t)，q͂(t)满足条件（ii）。由（i）和（ii）的结论可知：对于足够小的T，F是XT自身到自身的映射。

则对于0 ≤z≤1，0 ≤t≤T，只要T足够小，方程组（28）～（36）存在唯一解。

4 定理1的证明

证明 根据定理5，要证明方程组的解在0 ≤t＜T成立（其中T＞0且是任意的），只需证明

即式（12）成立。式（49）可由式（12）直接推出。而由文献［11］的引理4.2可知式（50）成立。证毕

5 定理2的证明

KR= 0意味着肿瘤中的死亡细胞完全没有消解，则通过式（38）有

因为R(t)关于t单调递增，同时营养物浓度σ(z，R(t))随着R(t)的增加而减少，故增殖率KB(σ)降低。从而当t→+∞时，无法得知R(t)趋于+∞还是保持有界。本节主要证明在假设（13）～（14）的基础上，R(t)趋于+∞. 假设（13）与实验事实相符，即死亡细胞倾向于集中在肿瘤的内部区域，而繁衍细胞倾向于集中在肿瘤的外部区域。而假设（14）基于事实：休眠细胞的死亡速率大于繁衍细胞的死亡速率。

首先我们需要给出以下初步引理：

引理4 令KR= 0并假设（13）～（14）成立，则

因为∀t≥0，有v(0，t)=v(1，t)= 0，故由比较原理可得v≤0. 证毕

令pˉ=pˉ(z，t)是下列初值问题