基于快速稀疏正则化的旋转梁损伤识别*

杨达豪，吕中荣，汪利

中山大学航空航天学院，广东广州 510006

在工程中，风机叶片［1］、直升机叶片［2］等是相关结构的重要部件，并且可以简化成旋转梁模型。在长期的工作环境下，这些重要部件容易产生裂纹、发生损伤、甚至断裂，严重地影响使用安全和经济效益。为此，有必要对旋转梁实行结构健康监测，维护整体结构正常运作。已有的研究表明，旋转梁会发生大幅运动和微弹性变形［3］；在科氏力和离心力的作用下，容易产生刚度效应［4-5］。为此，引入非笛卡尔坐标系变量延伸变形s（stretch deformation）与笛卡尔坐标系变量翼弦变形v（chordwise deformation）、挥舞变形w（flapwise deformation），以建立可以反映旋转梁更为真实运动的线性偏微分方程，并且使用有限单元法进一步得到离散方程［6］。

结构损伤识别是典型的反问题，在噪声影响或者数据不足的情况下，该反问题往往是一个病态的待求解目标方程。为了克服该弊端，需要引入正则化约束，如Tikhonov 正则化［7-8］，稀疏正则化［9-11］。Tikhonov 正则化是L2 范数并具有连续可导性质。目标方程在引入Tikhonov 正则化之后，可以通过SVD 分解，获得解析解，但正则化参数仍然由L-curve 曲线确定［7］。实际上，结构损伤数目是具有稀疏性的，即损伤数目应该是少量的，这与稀疏正则化所呈现的性质一致。为此，本文使用稀疏正则化求解目标函数，以呈现更好的鲁棒性。稀疏正则化项即L1 正则化项，由于不具有连续可导性质，使得目标方程求解显得较为困难。目前已有较为成熟的算法［10］，如LASSO 法（least absolute selection and shrinkage operator）、内点法（interior point method）、主动集法（active set method）。但这些方法都需要确定一个合适的稀疏正则化参数。已有的稀疏正则化参数确定方法有［11］：L-curve曲线法，差异原则法（method of discrepancy principle）以及广义交叉验证法（GCV，generalized cross-validation method）等。这些方法应用较为广泛，但容易受到噪声的影响且不可避免地有着计算代价高的缺点。为克服此类缺点，本文提出一种受摩擦模型启发的快速稀疏正则化方法。该方法指出，引入稀疏正则化相当于引入摩擦效应，其中稀疏正则化参数对应于静摩擦力。基于摩擦模型的物理意义，可直接选定某个摩擦力为正则化参数，从而快速求解目标函数，识别损伤程度和位置。数值算例表明，该方法具有效率高、鲁棒性强的优势。

1 旋转梁动力模型

如图1所示，旋转梁的长度为L，质量密度为ρ，杨氏模量为E，截面面积为A，关于y轴和z轴的极惯性矩为Iy，Iz，且有Iy=Iz。给定旋转速度Ω，旋转梁上一点从P运动到P'，其位移向量设为dr。在笛卡尔坐标系下，该点的运动速度（证明见附录）为［12］：

图1 旋转梁模型Fig. 1 Configuration of a rotating cantilever beam

其中dw、dsv分别是挥舞运动变形向量，翼弦变形向量；Sw、Ssv是由旋转运动所产生的刚度矩阵，Gsv是陀螺矩阵（gyroscopic matrix）；Msv、Mw是质量矩阵；Kw、Ksv是刚度矩阵。显然，方程（4）、（5）分别表征旋转梁的挥舞运动方程、翼弦运动方程。考虑匀速旋转的情况，即Ω̇ = 0，通过求解方程（4）、（5）的特征值问题［13］，可以获得旋转梁的模态数据，包括固有频率λ（特征值）和模态φ（特征向量）。

2 目标函数

结构损伤通常表现为系统刚度的局部减小，即相关单元刚度发生折减。设损伤系数为pi，pi⊆(-1，0]，其中i表示的是第i个单元。pi= -1时表示第i个单元断裂，即完全损伤；pi= 0时表示第i个单元完好。一般，损伤位置是稀疏的，即系统的损伤参数p=[p1，p2，p3，...，pn]具有少量非零元素，即具有稀疏性。

系统刚度可以写成关于损伤参数的函数，即

取最小值，其中W是一个权重矩阵。

方程（9）是一个非线性目标函数，可以通过迭代法进行求解，即：

①给定初始值p0=[0，0，0，...，0]。

②基于第（k- 1）步迭代结果，求解第k步的迭代值，即pk=pk-1+ Δp，其中Δp是在第k步求解得到的增量，k=[1，2，3，...，n]。

③当满足收敛条件的时候，结束迭代求解。

为了求得增量Δp或参数pk，在第k- 1步时，对R(pk)在pk-1处进行泰勒级数展开，即线性化处理

其中γ是正则化参数。通过求解方程（13）的最小值，即可求解得到增量Δp或参数pk.

3 快速稀疏正则化

为求解最终目标方程（13），首先要确定稀疏正则化参数γ。为此，可从一个由质量块、库伦摩擦单元、弹簧单元组成的多自由度摩擦模型出发，如图2 所示。基于该模型，可推导出正则化参数γ的表达式，即快速稀疏正则化。

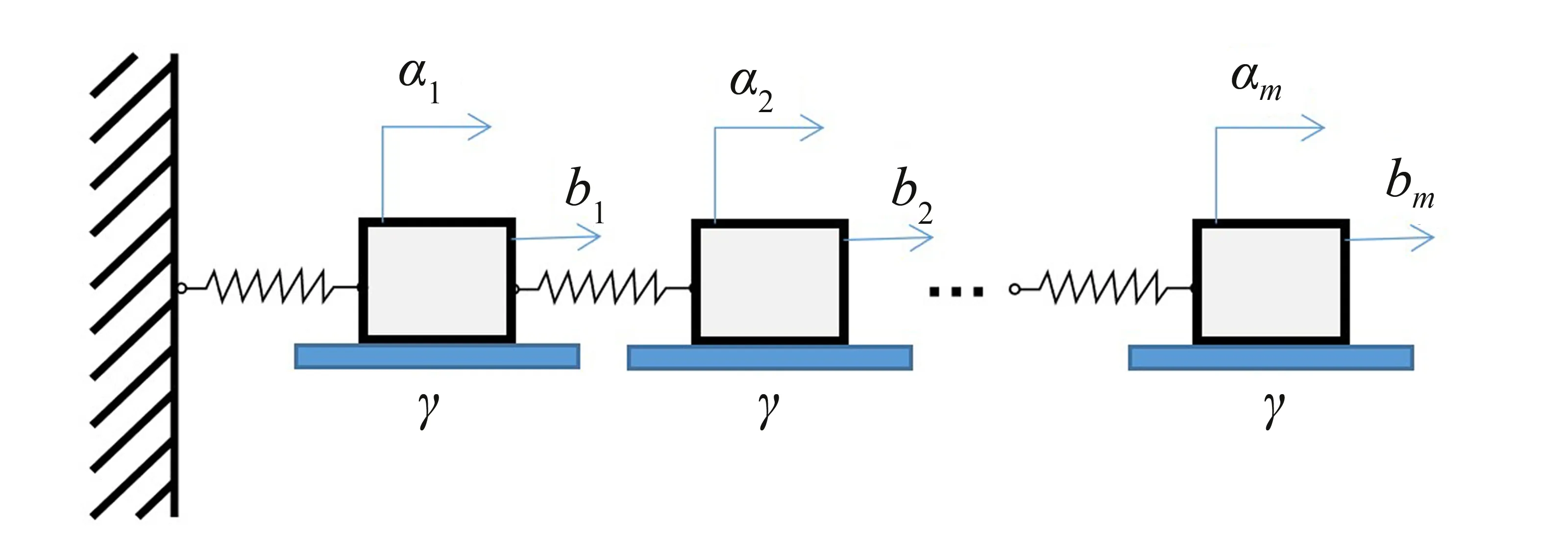
图2 快速稀疏正则化的物理摩擦模型Fig.2 Illustration of fast sparse regularization as a friction model

设整个物理摩擦模型系统所作的功为fγ(α)，即其中α、A、b、γ分别是质量块的位移向量、系统的刚度矩阵、外荷载向量、库伦摩擦单元的静摩擦力。方程（14）第一项表示弹簧存储的能量，第二项为外力做的功。方程（15）的第二项为摩擦消耗的能量，也就是说稀疏正则项的物理意义为能量耗散或外力做功［14］。

通过以上“摩擦力”的选择方程，即方程（20），可以有效控制解的稀疏性。方程（21）中的La在初始迭代时具有较大值，即正则化参数γ具有较小值，即“更多的滑块可以滑动”，这可以避免损伤程度和位置信息的丢失。在迭代一定次数之后，La具有最小值，此时γ取得最大值，即“只有个别的滑块可以滑动”，从而保证了最终结果的稀疏性。

4 数值算例

考虑一旋转梁，其长度L= 0.5 m，质量密度ρ= 2 700 kg/m3，杨氏模量E= 71GPa，截面面积A=10-4m2，关于y轴和z轴的极惯性矩Iy=Iz= 8.33× e-12m4。转台半径a= 0.1m。将旋转梁离散成11 个单元，设第3个单元发生损伤，损伤稀疏为pi= -0.3。考虑转速Ω= 30 rad/s。考虑特征值噪声为0.25%，特征向量噪声为5%。对于方程（21） 中La的选择，令d= 1，Lmin= 1，Lmax= 11。在无噪声情况下，N= 10；有噪声情况下，N= 100。基于快速稀疏正则化识别方法，只取前四阶模态数据即可取得较好的识别结果，基于挥舞模态数据和翼弦模态数据的损伤识别结果分别如图3-4 所示。为了进一步突出本文所提方法的有效性、快速性，选取L2正则化方法［7］进行识别结果对比。为了取得较好的识别结果，需要使用前六阶的模态数据。基于挥舞模态数据和翼弦模态数据的损伤识别结果分别如图5-6所示。

图3 基于挥舞模态数据的识别结果Fig. 3 The identification results based on the flapwise modal data

图4 基于翼弦模态数据的识别结果Fig. 4 The identification results based on the chordwise modal data

图5 基于挥舞模态数据的识别结果（使用L2正则化）Fig. 5 The identification results based on the flapwise modal data(with L2 method)

图3- 4 表明，在没有噪声的情况下，基于两种模态数据，快速稀疏正则化方法在第7 次迭代之后，识别结果已经接近于准确值。在有噪声的情况下，基于挥舞模态数据的识别结果要优于基于翼弦模态数据的识别结果，这是因为翼弦运动方程含有延伸变形，同时含有广义阻尼项2ΩGsv，使得翼弦运动方程更加复杂，容易受到转速的影响，求解相应的模态灵敏度也更加困难。在受到噪声的影响情况下，基于快速稀疏正则化的迭代收敛次数也仅20次。相比L-curve曲线方法等选择不同的正则化参数，快速稀疏正则化方法可以基于摩擦模型，直接选取“摩擦力”为正则化参数，在效率上具有显著优势［11］。此外，如图5-6 所示，L2 正则化在无噪声情况下，可以取得较为准确的识别结果，但是所需要的模态数据和迭代求解次数显著增加，这对数据采集的传感器、计算机性能提出了更高的要求。在噪声影响下，L2 正则化方法错误地识别若干单元具有损伤，并且p3的识别精度显著下降。由于翼弦模态响应更加复杂，L2 正则化识别方法在识别过程中也更加容易受到噪声数据的影响，如图6所示。

图6 基于翼弦模态数据的识别结果（使用L2正则化）Fig. 6 The identification results based on the chordwise modal data(with L2 method)

为了确定快速稀疏正则化方法的识别精度，各工况的识别结果列于表1。基于快速稀疏正则化的识别结果，最大的相对误差发生在基于翼弦模态数据（噪声）的第3个单元，仅为6.57%，表明所提方法具有较高的损伤识别精度和鲁棒性。基于L2 正则化的识别结果，该方法容易错误地识别单元损伤，最大误差发生在基于翼弦模态数据（噪声）（L2）的第六个单元，错误识别值为-0.053 6；最大相对误差发生在基于挥舞模态数据（噪声）（L2）的第3 个单元，为16.4%。综上，基于快速稀疏正则化方法不仅可以利用损伤位置和程度的稀疏性特性，提升识别结果的精度；还能准确地选择合适的正则化参数，提升收敛速度。

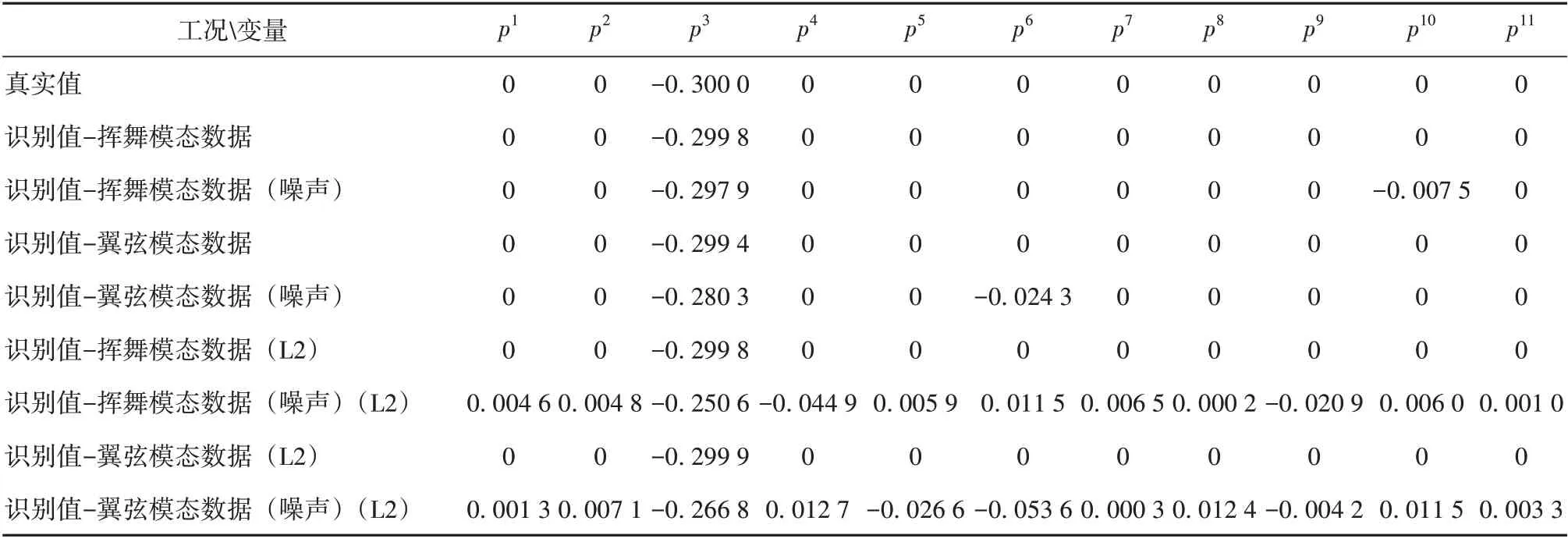
表1 基于快速稀疏正则化的旋转梁损伤识别结果Table 1 Identification result of rotating beam with the fast sparse regularization approach

5 小 结

本文提出一种快速稀疏正则化方法识别旋转梁的损伤。该方法从摩擦模型出发，指出正则化参数可以通过“摩擦力”大小直接确定，并能控制解的稀疏性。数值算例表明，通过对比L2 正则化方法和L-curve 方法，所提方法不仅计算效率高且可以准确快速地识别出旋转梁的损伤程度和位置。同时，所提的快速稀疏正则化方法表明，基于挥舞模态数据的识别结果要优于基于翼弦模态数据的识别结果，这是因为翼弦运动方程更为复杂，容易受到旋转速度的影响，且模态的灵敏度分析更为困难。

附 录

公式（1）是建立在旋转坐标系下。设惯性坐标系为oij，由于轴保持不变，平面发生旋转可表示成图7。图1中，P点运动到P'，P'的坐标rp为

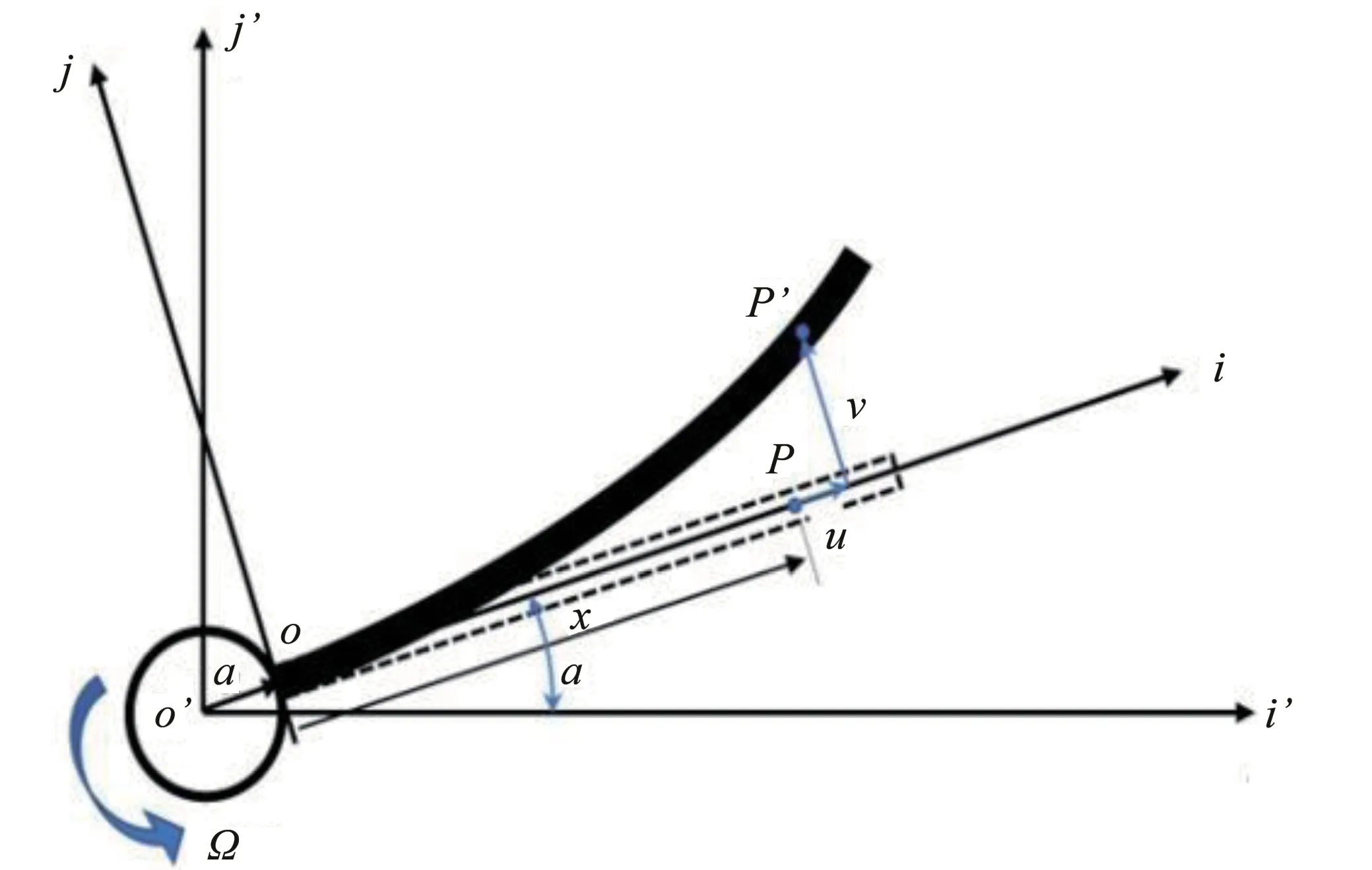
图7 旋转梁平面示意图Fig.7 Configuration of a rotating flexible cantilever beam in-plane deformation

其中α是转过的夹角，既有α̇=Ω，对公式（24）关于时间t求导，可得

将公式（25）带入公式（23），可得公式（1）。