基于自适应Kriging模型的人行斜拉桥有限元模型修正*

秦世强，廖思鹏，黄春雷，唐剑

武汉理工大学土木工程与建筑学院，湖北武汉 430070

在结构设计、施工、养护管理等领域，建立能够代表实际结构行为的有限元模型尤为关键［1］。由于建模过程简化和误差、结构参数的不确定性等因素［2］，导致有限元模型计算响应与实测响应之间存在一定差异；为此，通常需要对初始模型进行修正，从而获得能够代表实际结构的有限元模型。模型修正可看作优化问题，其目标函数由结构响应计算值和实测之间的残差构成。由于结构响应与设计参数之间为隐函数关系，在修正过程中需不断调用有限元模型来评估目标函数；若有限元模型复杂、单元数量多，这一过程会非常耗时。因此，利用代理模型显式地表达结构响应和设计参数之间的隐式关系，从而替代有限元模型进行目标函数评估，能够显著提高模型修正的效率。

常用的代理模型包括多项式响应面［3］、Kriging模型［4］、径向基函数［5］、支持向量回归［6］等，其中以地质统计学为基础的Kriging 模型因对所有样本点的精确插值具有比多项式响应面更高的近似精度［7］，且兼具局部与全局的统计特性，具有一定的代表性。Kriging 模型是一种方差估计最小的无偏估计模型，能够在给出未知函数的预测值的同时给出相应的误差。胡俊亮等［8］以频率和模态置信准则（MAC，modal assurance criterion）为修正目标，结合Kriging 模型对一大跨度钢管混凝土连续梁拱结构模型进行了修正；Khodaparast 等［9］利用Kriging 模型进行了区间模型修正；Liu 等［10］利用试验模态参数构建目标函数，结合Kriging 模型对一复杂结构进行了模型修正。以上研究在构建Kriging 模型时均采用一次性构建方法，即利用试验设计，一次性生成所有样本点。这种方法有2个缺点：1）样本点数量确定完全凭借分析者的经验；传统试验设计方法如中心复合设计，其样本点数量是由参数的维度确定的，但由于其样本点位置有重复，并不适用于模型修正这一类确定性的计算机试验；现代试验设计方法如拉丁超立方设计（LHD，latin hypercube design），其基本思想是均匀随机抽样，样本点的数量与参数的个数无关；而标准Kriging 模型样本点的数量是根据分析者经验确定的；样本点数量过大时，不仅导致计算工作量增大，而且会导致过拟合问题；若样本点数量过小，可能导致精度不足。2）在样本点数量合适的前提下，由于其空间位置的随机性，标准Kriging 模型即便通过均方根误差精度检测，也不能保证对目标函数极值区域的预测精度。本文采用自适应Kriging 模型进行模型修正，基本思路是通过先前少部分样本点构建的Kriging 模型对目标函数极值分布进行学习，控制后续增加的样本点分布在目标函数极值附近，使样本点在设计空间的位置更为合理，从而提高基于Kriging 模型的模型修正精度。

在可靠度评估方面，Chen 等［11］提出一种局部自适应采样方法，用于自适应地构建Kriging 模型；利用三个测试函数及一个蜂窝状结构的可靠度优化设计表明，自适应Kriging 模型同时具备精度和效率。在注塑成型优化设计方面，高月华等［12］提出一种同时考虑预测响应值及其不确定性的加点准则，自适应地构建了Kriging 模型，验证了自适应Kriging 模型的有效性。在桥梁动力可靠度方面，贾布裕等［13］将自适应策略加入到Kriging 模型，并首次建立了动力可靠度极限状态方程。然而，自适应Kriging 模型在模型修正领域的应用却相对较少。李永乐等［14］在进行车-线-桥耦合振动分析时，将自适应Kriging 模型用于修正无砟轨道的有限元模型，并对其进行了精度检验；杨修铭等［15］利用频响函数构建目标函数，结合自适应Kriging模型进行了模型修正。在上述研究的基础上，本文利用自适应Kriging 模型进行桥梁结构模型修正，通过CCD 估算初始样本点的数量，然后利用EI 准则和收敛准则控制新增样本点的位置和数量。同时，结合一座人行斜拉桥，分别利用标准Kriging模型和自适应Kriging 模型构建人行桥的代理模型，并基于环境振动试验获得的频率和振型，对该桥进行了有限元模型修正，验证了自适应Kriging 模型在实际工程应用中的可行性和优势。

1 理论基础

1.1 模型修正理论

有限元模型修正是通过修正结构设计参数，不断减小结构响应计算值和实测值之间的差异。模型修正是一个优化问题，其目标函数J(x)为

式中x表示待修正参数组成的向量，修正参数包括弹性模量、边界条件、材料容重、截面惯性矩等；ri(x)表示第i个响应计算值与实测值的残差函数；ωi为ri(x)的权重系数；nr表示模型修正中考虑的响应类型数量。常用于结构模型修正的响应类型包括静力位移、应变、频率、模态振型等。以位移为例，其残差函数rd(x)可表示为

1.2 Kriging模型

为了避免在修正过程调用复杂的有限元模型，需要将结构响应和修正参数之间的隐函数关系拟合成显函数。利用试验设计获得待修正参数和结构响应的样本后，可以进一步拟合结构响应关于修正参数的Kriging 模型。Kriging 模型由两部分组成：线性回归和非参数部分。即

式中ŷ(x)表示结构响应的Kriging 模型预估值；f(β，x)为多项式函数，用于模拟样本点的总体趋势；β为多项式回归系数矩阵；z(x)为一随机过程，服从均值为0、方差为σ2的正态分布，用于模拟样本点局部近似。由于z(x)的存在，Kriging 模型更适合于近似具有复杂非线性的结构输入、输出模型。Kriging 模型常用的精度测试指标如R2、均方根误差RMSE 等［4］，关于Kriging 模型完整的理论推导过程可参考文献［16］。

2 自适应Kriging模型

2.1 试验设计及样本点数量确定

为了获取结构响应和待修正参数的样本，首先需要通过试验设计获得待修正参数在设计空间内的样本，然后结合有限元模型计算结构响应。目前，试验设计方法可分为传统试验设计方法，和现代试验设计方法两类。传统试验设计方法适用于物理试验，其特点是样本点位置相同，但试验结果仍有可能不同。现代试验设计方法主要采用了空间填充的思想，其样本点数量不固定且位置不重合，更适合于计算机试验。本文选用拉丁超立方设计用于生成修正参数样本点。LHD 是一种多维分层抽样试验设计方法，其样本点H(i)j为

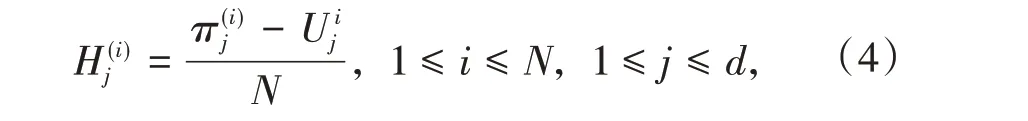
式中π为1到N的独立随机排列数；U为在［0，1］之间独立于π的随机数；下标j为修正参数的维数，上标i为修正参数的水平数。

对于LHD 样本点数量的确定，自适应Kriging模型首先需要确定一个初始样本集，然后根据最大期望准则控制后续新增加点的数量。韩忠华［17］曾指出，自适应Kriging 初始样本集数量的选择，并不受设计空间维度的限制，只需满足代理模型精度要求即可；可见，目前并无明确的方法确定现代试验设计方法及Kriging 模型的样本点数量。为此，本文采用CCD 来估算自适应Kriging 模型的初始样本集数量；并结合收敛准则自适应地控制新增样本点数量，即样本点总数由算法自身确定。为了保证可比性，标准Kriging 模型的样本点总数与自适应Kriging模型相等。

2.2 自适应加点准则

自适应Kriging 模型是通过初始样本集获取目标函数在设计空间的分布状况，使得后续新增的样本点位于目标函数极值处或预测误差较大的位置，不断提升Kriging 模型的精度；当达到一定的条件时，新增样本点的过程终止，Kriging 模型构建完毕。本文通过初始样本集得到Kriging 模型对未知点x的预测值和预测标准差后，根据最大期望改善（EI，expected improvement）准则，将EI 函数值作为评价指标，来代表设计空间内任意点对当前样本集中的最优值的改善程度I(x)，选择使EI函数值最大点所对应的样本点作为最佳样本点，将该样本点添加到最初的样本集中更新Kriging 模型，如此循环迭代直至收敛。假设当前样本集内最优值为ymin，Kriging 模型对未知点的预测值ŷ服从均值为-y、方差为s2(x)的正态分布。I(x)定义为

函数I(x)的期望（即EI函数）可表示为

式中Φ和ψ分别代表标准正态累积分布函数和标准正态分布概率密度函数。通过优化算法寻找到EI函数值最大点所对应的样本点作为更新点添加到样本空间中，不断更新模型，使得Kriging 模型根据不同的工程实际问题的特性来自适应地选择样本点；其收敛准则为

即当最大EI 值与当前最优响应值yopt小于收敛阈值σ时，不再新增加样本点；σ可根据问题的精度需求确定；若取为1× 10-3，则表示新增样本点后的最大EI 值与当前最优值之比＜1× 10-3，此精度水平对结构模型修正而言已经足够。

2.3 基于自适应Kriging模型的模型修正流程

基于自适应Kriging模型的模型修正流程为：

1）根据设计图纸建立结构有限元模型，基于工程经验和敏感性分析选择待修正参数；同时，完成实际结构测试，并建立目标函数；

2）根据修正参数的个数，结合CCD 确定初始样本点数量；利用LHD 生成初始样本点，并结合初始有限元模型计算样本点对应的结构响应；

3）利用初始样本集构建Kriging 模型，以标准遗传算法（GA，genetic algorithm）［18］进行迭代，寻找在当前模型基础上使EI 函数值最大的样本点作为新增样本点；

4）结合有限元模型计算新增样本点对应的结构响应，并用于更新Kriging模型；

5）重复第3～4步，直至满足式（7）中的收敛要求；

6）对构建的Kriging 模型进行精度测试；若满足精度要求，进入第7 步；若不满足，重复3～5步；

7）利用优化算法寻找目标函数在设计空间内的极值；目标函数中的响应计算值由构建好的Kriging模型提供，实测值由试验数据提供；

8）评估模型修正效果。

3 测试函数

为了测试自适应Kriging 模型相对于标准Kriging 模型的精度，本文选取了六背驼峰函数以及Goldstein-Price（GP）函数作为测试函数。六驼峰函数为

式中F（x）表示测试函数的函数值；x表示自变量；对六驼峰函数，-2 ≤x1≤2，-1 ≤x2≤1；在（0.089 8，-0.712 6）和（-0.089 8，0.712 6）有相同的全局最小值为-1.031 6；对GP 函数，-1 ≤x1，2≤1；在（0，-1）处有全局最小值0.477 12。

采用LHD 构建初始的样本点，在构建的初始Kriging模型的基础上，利用GA对EI函数进行寻优来更新模型直到满足收敛条件为止。GA 参数设置为种群数目为500，迭代次数为200，交叉几率为0.9，变异几率为0.1。

根据Matlab 中的命令ccdesign，对CCD，当问题维度为2时样本点数量为16。因此自适应Kriging模型的初始样本点数量取为16；由于测试函数有明确的函数形式，计算精度较高，因此自适应Kriging 模型的收敛阈值σ取为1× 10-6；最终，六驼峰函数和GP 函数在初始样本点的基础上，分别新增加了28 和33 个样本点，即总样本点数量分别为44 和49。对于标准Kriging 模型，则保持总样本点数量与自适应Kriging 模型相同，利用LHD 一次性抽取44 和49 个样本点；图1 和图2 分别给出了两个测试函数的标准Kriging 样本点和自适应Kriging 样本点，可以看到，通过自适应地添加样本点的方式，两个测试函数新增加的样本点主要位于边界和函数极值附近。

对构建好的两种Kriging 模型，采用标准粒子群优化算法（PSO，particle swarm optimization）［19］寻找测试函数在定义域内的最小值，PSO参数为种群数目为30，最大迭代次数为100，速度惯性取0.729，学习因子为2。为获得统计上有意义的比较结果，避免算法的不确定性，对每个测试函数进行了200 次独立运算。表1 给出了利用不同Kriging 模型的精度评价和PSO 优化结果。从表1 可看出：（1）在样本点总数相等的前提下，对两个测试函数，构建的标准Kriging 模型和自适应Kriging模型的R2均大于0.97；RMSE 最大不超过0.039 3；表明标准Kriging 模型和自适应Kriging 模型均具备较高的精度；（2）进一步地，利用PSO 去寻找两个函数的最小值，并进行200次独立计算，分析计算结果的均值和标准差；对六驼峰函数，标准Kriging 模型和自适应Kriging 模型的均值较为接近，且均接近于理论解，但自适应Kriging 模型的结果精度和稳定性更高；对GP 函数，Kriging 模型的均值为0.47，偏离理论解较多；而自适应Kriging 模型的均值为0.84，接近理论解。这主要是因为标准Kriging 模型一次生成的样本点具有一定的随机性。从图2 可看出，在函数极值（0，-1）附近区域点数较少，导致无法准确预测目标函数极值；而自适应Kriging 模型则较好地避免了这个问题。测试函数结果表明，自适应Kriging 能够避免样本点在空间分布的随机性，提高模型对目标函数极值区域的预测精度。

图2 标准Kriging和自适应Kriging样本点（GP函数）Fig.2 Standard Kriging sample points and Adaptive Kriging sample points(GP functions)

表1 不同Kriging模型的函数值搜索结果Table 1 Function value search results of different Kriging models

4 人行斜拉桥模型修正

4.1 工程概况

理工一桥是一座主跨为45.0 m 的独塔人行斜拉桥，桥跨布置为（20.0+45.0+21.3）m。主梁为钢箱梁结构，高0.7 m，如图3 所示。主梁由直线段和U 型曲线段组成，直线段桥面宽7.0 m，曲线段桥面宽分别为3.5 m 和4.0 m。桥塔采用变截面矩形钢箱结构，高25.0 m，在桥塔两侧各布置4根拉索。主塔上最高拉索的锚固点距离桥面16.98 m，最低拉索的锚固点为6.48 m，锚固点相互间距为3.50 m。8 根斜拉索中，最长拉索长为34.761 m，最短拉索长为10.618 m，采用主塔端固定和主梁端张拉。根据设计图纸，基于ANSYS 软件建立了理工一桥的初始有限元模型（图4）。主梁及主塔采用Shell63单元模拟，其弹性模量为210 GPa，质量密度为7 900 kg/m3；斜拉索采用Link10 单元模拟，其材料弹性模拟为202 GPa，质量密度7 900 kg/m3。边界条件按照图纸设置，主梁与主塔采取固结方式，边墩处设置两个板式橡胶支座。

图3 理工一桥立面图及平面图（单位：m）Fig.3 The elevation and plan view of Ligong First Bridge(unit:m)

图4 理工一桥ANSYS有限元模型Fig.4 The ANSYS finite element model of Ligong First Bridge

4.2 环境振动试验

为了获得理工一桥的模态参数，对其进行环境振动试验。环境振动试验利用5个无线加速度传感器，测试桥面在环境荷载下的竖向和横向加速度，并结合协方差驱动的随机子空间识别算法识别桥梁的频率和振型。在桥面两侧平均每隔3 m 布置1个测点，共计布置了53个测点，其中2个为参考点，其余测点通过移动传感器分17 个测试组完成；每个测试组采样时间约为15 min，采样频率为200 Hz。表2 对比了试验识别的前4 阶频率的计算值和试验值，并给出了振型的MAC值；可以看出，前4 阶模态振型试验值与计算值的MAC 值均大于0.93，表明振型识别结果较好。频率方面，试验值和计算值的相对误差均未超过10%，最大相对误差为7.02%，表明初始有限元模型与实际结构吻合较好，但频率计算值仍有修正空间。

表2 频率和振型实测值与计算值Table 2 The frequencies and mode shapes of experimental identified and analytical values

4.3 修正参数与目标函数

修正参数的选择上，一方面考虑到理工一桥主梁、主塔为钢箱梁，其截面制造精度较高，因此截面惯性矩未作为修正参数；另一方面，初始模型建立过程中忽略了一些局部加劲肋、焊缝和螺栓，这些会影响到结构的刚度和质量分布，因此修正参数的选择范围主要是结构的弹性模量、质量密度；此外，由于斜拉桥的索力对结构响应影响较大，因此斜拉索的初始张拉力也纳入修正参数的选择范围。在上述思路下，首先选了13 个结构设计参数作为待修正参数，然后进行参数的频率和模态振型灵敏度分析，选择灵敏度高的参数作为最终的修正参数。这13 个待修正参数分别是：主塔、T 型桥墩、主跨箱梁、边跨箱梁、圆弧段箱梁和斜拉索的弹性模量（用E1-E6 表示）和质量密度（用P1-P6 表示）；斜拉索的初始拉应变（用stra 表示）。除了E6的设计值为202 GPa 外，其余构件的弹性模量设计值均为210 GPa；所有质量密度的设计值均为7 900 kg/m3；斜拉索的初始拉应变为7.47×10-3。

对上述13 个待修正参数进行频率灵敏度和振型灵敏度计算，计算结果如图5 所示。可以看出，主跨箱型梁的弹性模量E3 和其质量密度P3、圆弧曲线端箱梁的弹性模量E5和其质量密度P5对理工一桥的模态频率fi敏感性相对较高；主跨箱型梁质量密度P3和圆弧曲线端箱梁的质量密度P5对理工一桥的模态振型敏感性相对较高。综合考虑，选择E3、E4、E5、P3 和P5 五个设计数作为修正参数进行模型修正。按照式（1），目标函数由前4阶频率和模态振型的MAC 构建。为保证修正后的参数物理意义，修正过程中各参数的上下界分别为其初始值的1.25和0.75倍。

图5 设计参数敏感度分析Fig.5 The sensitivity analysis of design parameters

4.4 自适应Kriging模型

对于5参数问题，CCD的样本点数量为46，因此自适应Kriging 模型的初始样本点数量为46。利用LHD 获得初始样本点的空间分布后，结合有限元模型计算样本点对应的频率和振型；后续新增样本点则由EI 准则控制，收敛阈值取为0.01。最终，共计新增了28 个样本点，即总样本点的数量为74。为保持样本点总数一致，Kriging 模型的样本点数量取为74。以一阶频率关于修正参数E3 和E5 的函数关系为例，标准Kriging 和自适应Kriging拟合的Kriging 响应面分别如图6 所示。可以看出，标准Kriging 模型的样本点基本上随机地布满设计空间；自适应Kriging 模型的初始样本点也是随机布满空间，但新增的样本点则一部分集中于边界，另一部分位于E3［0.7， 0.9］的区间内；这表明自适应Kriging 模型的新增样本点更具有指向性，即更多分布于RMSE 较大的位置和函数极值区域。表3 给出了标准Kriging 模型和自适应Kriging 模型的R2和RMSE，以评价二者的精度。可以看出，两个模型的前四阶频率的R2＞0.99，RMSE 值均小于1.07×10-3；除第四阶振型外，前三阶的振型的R2均大于0.97；RMSE 均小于0.54×10-3；表明标准Kriging和自适应Kriging模型的拟合精度较高。

图6 标准Kriging和自适应Kriging拟合的一阶频率响应面Fig.6 The 1st order frequency response sufarce fitted by standard Kriging and Adaptive Kriging

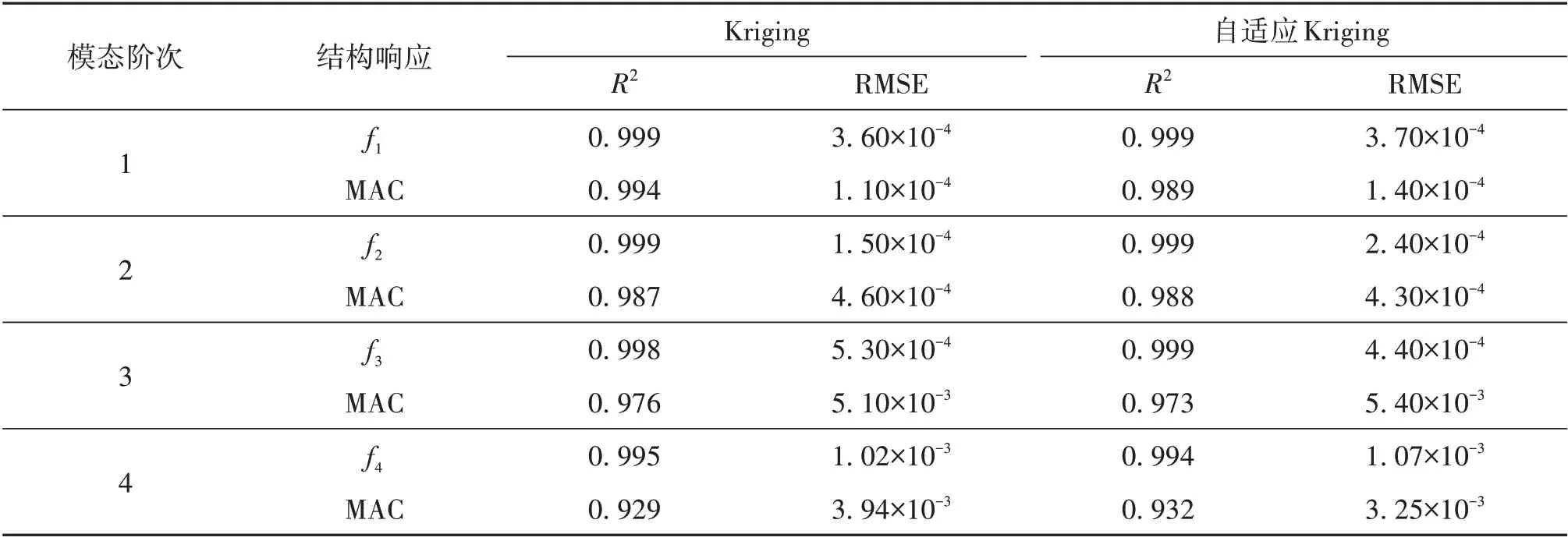
表3 Kriging模型和自适应Kriging模型的精度Table 3 The accuracy of Kriging and Adaptive Kriging model

4.5 结果分析

采用PSO 算法在设计空间内搜索目标函数的最小值；其中，目标函数的计算值分别由标准Krigin 和自适应Kriging 模型预测，试验值根据实测结果确定。PSO 算法的种群数量取为30，最大迭代次数取100，速度惯性取0.729，社会和认知系数均取为2.0，上述参数均为标准PSO 的默认参数，其合理性已经得到大量工程算例验证。

表4列出了各修正参数在修正前后的对比，可以看出：（1）除E4 外，两种模型的修正结果变化趋势基本一致；（2）自适应Kriging 模型的修正结果中，E3 相比其初始值降低了20.9%，即为其初始值的0.79 倍，这与前述自适应Kriging 新增样本点的位置是一致的，表明自适应Kriging 通过评估初始样本集，找到了目标函数极值所在的区域，并对其该区域的样本点数量进行了增加。需要说明的是，修正参数在修正前后的变化，并非代表材料特性发生了变化，只是表征初始模型和实际结构之间的质量或刚度差异；因此可以理解为等效弹性模量或等效密度；类似的修正幅度在现有文献中也有描述，如文献［20］对一座斜拉桥的模型修正，主梁的密度修正幅度达到17.9%。

表4 模型修正前后的修正参数值Table 4 The updating parameters before and after model updating

表5 给出了修正前后的频率和MAC 与试验值的对比，可以看出：（1）经过模型修正，相比初始模型，两种Kriging 模型的修正结果均与试验值更为接近；例如第一阶频率相对误差由修正前的7.02%降低到修正后的3.08%和2.81%；其余各阶频率精度均有不同程度的提升；相比修正前，修正后的MAC 也有小幅提升；（2）相比标准Kriging 模型，自适应Kriging 模型获得了更好的修正精度。上述修正结果表明，在样本点数量一致的前提下，自适应Kriging 模型能获得比Kriging 模型更好的修正精度。图7给出了前四阶实测振型和自适应Kriging 修正后的模型计算振型对比图，可以看出，经过模型修正，各振型与实测振型吻合良好。

图7 模态振型试验值和自适应Kriging修正值Fig.7 The mode shapes of experimental values and updated values obtained from Adaptive Kriging

表5 修正结果对比Table 5 The comparison of the updating results

5 结 语

本文构建了一种基于自适应Kriging 模型的有限元模型修正方法，并且提出了一种样本点总数的确定方法。与标准Kriging 模型一次性生成所有样本点不同，该方法首先通过CCD 估算初始样本集的数量，利用LHD 生成样本点的空间位置，并初步构建Kriging 模型；然后利用EI 准则自适应地控制新增样本点的位置，直至满足收敛准则。通过测试函数和理工一桥模型修正对比了标准Kriging 模型、自适应Kriging 模型精度以及修正结果，可得到如下结论：

1）测试函数表明：在样本点总数一致的情况下，通过计算R2和RMSE，可知自适应Kriging 模型和标准Kriging 模型具有相近的预测精度；但由于自适应Kriging 模型中后续增加的样本点多位于目标函数极值附近，因此在函数极值附近，自适应Kriging 能够提供比标准Kriging 更高预测精度；此外，GP 测试函数还表明，即便Kriging 模型通过R2和RMSE 精度测试，由于样本点分布的随机性，Kriging 模型对函数极值区域预测精度可能不足，从而导致后续优化结果不正确。

2）理工一桥模型修正案例表明：通过CCD 初步估算样本点数量，并结合收敛准则控制新增样本点数量，确定的样本点总数基本合理。在样本点总数一致的情况下，自适应Kriging 模型和标准Kriging 模型的精度基本相仿，但自适应Kriging 模型能够避免样本点空间分布的随机性，提高对目标函数极值区域的预测精度，从而获得更好修正结果。