奥氏体不锈钢应力腐蚀微裂纹的非线性表面波检测

(大连理工大学 材料科学与工程学院，大连 116024)

在石油、核工业等领域中，奥氏体不锈钢因具有良好的性能而被广泛应用，但其长期处于应力及腐蚀的环境中，材料内部会发生位错、滑移等微观损伤，这些微观损伤会逐渐孕育形成微裂纹，当应力或腐蚀达到一定程度时，微裂纹将进一步扩展形成宏观裂纹，显著降低设备的力学性能，严重时还会导致金属材料的突发性脆断。通常，微裂纹孕育阶段占据结构由正常使用到失效破坏的总寿命的90%[1-2]。因此，及时检测出结构中的微裂纹等损伤显得尤为重要。

随着无损检测技术的发展，非线性超声检测凭借其灵敏度高、对微裂纹敏感等优点得到了广泛的应用。非线性超声检测是利用超声波在材料中传播时，其与介质或微观缺陷相互作用而产生的非线性响应信号对早期损伤进行评价，以反映材料应力-应变的非线性[3]。非线性超声检测现在已被用于金属构件的疲劳微裂纹检测、金属基结构界面黏接强度评价、力学性能退化评估[4]等领域中。ZEITVOGEL等[5]研究使用非线性瑞利波来表征碳钢中的应力腐蚀开裂(SCC)损伤，试验发现，在SCC的早期阶段，所测量的声学非线性有所增加，表明了使用非线性超声检测碳钢中的SCC损伤具有可行性。

数值模拟技术的发展拓宽了非线性超声检测的研究思路。梁泽龙[6]基于ABAQUS软件，提出了一种建立应力场与声场联系的分析方法，实现了受载条件下的混凝土超声传播模拟。

利用非线性超声检测微裂纹的研究多数是在无应力状态下进行的，对于恒应力作用下的微裂纹检测则少有报道，目前所实现的受载条件下对超声波传播特性的研究分析步骤也相对复杂。笔者利用COMSOL 多物理场仿真软件，优化创建了奥氏体不锈钢应力腐蚀微裂纹的非线性表面波检测模型，探讨了不同参数设置对模拟结果的影响，结合试验分析验证了COMSOL软件在求解非线性表面波检测应力腐蚀微裂纹问题上的可行性与优越性。

1 基于COMSOL软件构建并优化微裂纹表面波检测模型

1.1 构建几何模型

结合奥氏体不锈钢设备服役过程中可能发生的缺陷腐蚀情况，简化设备结构，按照以下基本参数绘制尺寸(长×宽)为35 mm×5 mm的二维模型，材料为奥氏体不锈钢，微裂纹的初始大小为50 nm ×0.3 mm(长×宽)。微裂纹的模拟选择直接在几何模型上去除自定义大小的实体单元，该方法能够在后续的网格划分中，在微裂纹附近加密网格，获得较高的仿真精度。利用COMSOL软件建立的非线性表面波检测微裂纹的二维模型如图1所示。奥氏体不锈钢材料参数如表1所示。

图1 非线性表面波检测微裂纹的二维模型

弹性模量/GPa密度/(kg·m-3)泊松比抗拉强度/MPa屈服强度/MPa1957 9300.28540230

1.2 激励信号

在采用COMSOL软件模拟时，将激励信号以指定位移的形式施加在几何模型中距离左边界5 mm处，作为检测的发射声源。

选取合适的激励信号进行超声波模拟，能提高缺陷检测的准确性。针对表面微裂纹损伤，选择能量集中于固体表面及近表面传播的表面波进行检测。单脉冲信号、连续正弦信号、正弦调制信号这3种信号都能激发产生表面波，其中正弦调制信号结合了单脉冲信号与连续正弦信号的优点，既能产生检测所需的连续振动，又能保证超声波能量集中，具有较高的振幅，能与微裂纹相互作用产生明显的非线性效应。选择汉宁窗调制的连续正弦信号作为模型的激励信号，激励信号的中心频率根据实际超声检测探头的频率选定为2.5 MHz，周期数为10，激励信号如式(1)所示。

(1)

式中：X(t)为激励信号对介质的指定位移；A为信号的幅值；f为中心频率；t为时间,且t<4 μs。

1.3 网格的划分

网格划分是生成计算所需的节点和单元，建立有限元模型的一个重要环节，所划分的网格形式对计算精度和计算规模将产生直接影响[7]。网格尺寸过大会降低计算精度；网格尺寸过小，则需要大量的计算资源[8]，增加模型计算时间。COMSOL软件下固体力学弹性波接口的默认设置是使用四次(四阶)形函数，每个波长仅需要约 1.5 个网格单元。

采用最大频率分量f为5 MHz，CR为表面波的波速，则计算出最大的网格尺寸L≤0.38 mm(L为网格边长)。

综上所述，为了保证结果更加精确，运算时间更加合理，模型设置最大网格边长为0.1 mm，网格的类型为自由三角形。

1.4 时间步长

时间步长的选取直接影响求解精度，时间步长过大会导致计算结果精度低；时间步长过小，则需要较大的电脑内存和过长的运算时间。为使求解过程准确，时间步长必须满足奈奎斯特定理和Moser定理[9]。

奈奎斯特频率是指允许的最低抽样率，即采样频率应不小于实际信号频率的2倍[10]，则时间步长∇t1≤10×10-8s。

Moser定理是指一个周期的时间内至少包含20个时间步，则时间步长∇t2≤2×10-8s。

综合考虑，设置瞬态求解器的时间步长为2×10-8s，求解的总时间应大于表面波传播至接收点的时间，设置为2×10-5s。

1.5 边界条件

1.5.1 低反射边界

由于模型的计算域尺寸很小，当表面波传播至模型的边界时，会发生很强的反射，反射波与激励信号产生混叠，对接收信号产生干扰。因此，为了降低模型边界反射信号的干扰，在模型边界处设置低反射边界。图2为某一时刻有、无低反射边界的位移云图和接收信号时域对比图，可以明显看出，设置低反射边界有效地减少了模型边界处的反射波效应，使得各种模式波的波阵面更加连续顺畅，保证了仿真结果的精确度。

图2 有、无低反射边界的位移云图和接收信号时域对比图

1.5.2 接触

结构中非线性的主要来源有经典声非线性和接触声非线性[11-12]。经典声非线性是材料本身的固有属性，主要与材料固有的物理特性有关。接触声非线性反映了材料局部的缺陷特征，其主要来源于界面、裂纹缺陷、接触面的非线性应力-应变等，检测过程中超声波振动使微裂纹界面发生周期性的张开或闭合，两个接触面相互撞击和摩擦，这种裂纹张开或闭合的状态导致其界面间存在各种应力-应变关系，其叠加会使得超声波信号产生非线性失真[13]，出现高次谐波。笔者所研究的非线性超声检测应力腐蚀微裂纹问题则属于接触声非线性范畴。因此，在创建微裂纹损伤的非线性表面波检测模型时不能忽略微裂纹的接触声非线性，需将微裂纹的两条边界定义为接触对(分别为源边界与目标边界)，以确保创建的非线性超声波检测微裂纹模型更合理，较好地实现非线性表面波对微裂纹的检测识别。

1.6 应力场与超声场的耦合

实际情况下，无论是应力腐蚀还是疲劳腐蚀，都是处于受力状态下的腐蚀损伤。在利用非线性表面波检测应力腐蚀微裂纹的研究中，涉及的物理场有应力场与声场两部分，模拟中需实现应力场与声场的耦合。文中研究对象为固体，声场的激发采用施加指定位移振动来实现，故应力场与声场两部分的模拟都在固体力学(弹性波)模块下进行。物理场的耦合方式分为直接耦合与顺序耦合(或间接耦合)两种，可针对不同的模型问题来选择。

1.6.1 顺序耦合

若含微裂纹的模型受恒应力作用后再进行超声检测，即先进行“静态力分析”，再进行“瞬态声场分析”，声力过程并非同时计算，此时为顺序耦合。

图3 顺序耦合得到的接收信号时域图与频域图

此顺序耦合的思路与石媛媛等[14]应用ANSYS和ABAQUS两种有限元模拟软件，并以重构的方法实现应力场与超声耦合的思路相似，但该研究仅利用单一COMSOL软件就实现了应力场与声场的耦合，在很大程度上简化了建模步骤，缩短了模拟运算时间。

1.6.2 直接耦合

图4 直接耦合接收信号及微裂纹处变形的时域图与幅频图

若考虑裂纹边界受载后的尺寸及状态随时间演化的过程，整个求解过程是瞬态的，恒应力与表面波同时加载到模型上进行瞬态分析计算，为直接耦合。

接收信号的时域图如图4(a) 所示(应力为3 MPa)，可看出直接耦合模型最终接收的时域信号在5 μs附近有波形出现，考虑该波是由恒应力波与声场中的纵波叠加而成的，原因为裂纹受应力作用后其变形不是一步到位。采用瞬态求解记录了其在短时间内发生变形然后达到相对稳定的过程，此过程同时伴随低频应力波的产生，图4(b)为微裂纹变形过程的信号，对其进行傅里叶变换得到的幅频曲线如图4(c)所示，结果证实：恒应力加载到微裂纹边界处，在0 Hz附近产生了低频信号。分析模型接收信号的频域成分，发现有二次谐波出现，同时在0 Hz附近也出现了低频成分，此低频成分即为高频的激励信号与恒应力产生的低频信号调制形成。计算其非线性系数为5.77×10-3，此结果与顺序耦合非线性结果比较接近。

在上述基础上，对比顺序耦合与直接耦合方式对模拟结果的不同影响，选定压应力分别为1 MPa和无应力，拉应力分别为1，2，3 MPa，这5组应力数据分别作用于裂纹边界，利用顺序耦合与直接耦合两种方式进行模拟计算，施加的恒应力与非线性系数的关系曲线如图5所示。

图5 恒应力与非线性系数的关系曲线

随着施加在微裂纹边界处拉应力的增加，直接耦合和顺序耦合两种方式的非线性响应都明显降低，压应力的非线性响应大于拉应力的，这是由于拉应力使裂纹开口变大，抑制了高次谐波的产生，而压应力则反之；相同的受载状态下，顺序耦合与直接耦合的超声波非线性响应程度几乎相同，这是由于超声波作用力大于裂纹边界施加的恒应力，直接耦合中恒应力产生的波对接收信号的影响较小，但是随着恒应力的增加，恒应力波调制作用增强，直接耦合中高次谐波的幅值降低，非线性系数低于顺序耦合的，二者的响应程度差距逐渐变大。因此，在不影响检测结果的前提下，可选择建模和计算更加便捷的直接耦合方式来实现应力场与声场的耦合。

2 非线性表面波检测应力腐蚀微裂纹的模拟结果分析

图6 模拟得到的微裂纹4个时刻的位移云图

采用最优模型进行微裂纹的非线性表面波检测有限元模拟，依次得出4个时刻的位移云图如图6所示。由图6可以看出，从激发点开始，横波与纵波沿竖直方向呈半圆形传播并且能量逐渐降低，直至模型边界处被低反射边界吸收，无反射现象；随着传播时间与传播距离的增加，声波能量集中在模型表面。结合图4(a)，根据激发、接收位置的关系和接收信号时间，计算得出该声波的波速为2 906 m·s-1，这与理论中表面波在奥氏体不锈钢中的传播速度接近，从理论上证明了模型的正确性。

2.1 恒应力作用下微裂纹深度对非线性表面波传播行为的影响

应用该模型探索恒应力作用下微裂纹深度与非线性响应大小的规律，固定微裂纹的宽度为50 nm，拉应力为1 MPa，分别选取深度为100，150，200，250，300 μm的微裂纹进行模拟计算，对比结果发现：随着微裂纹深度的增加，时域信号的幅值明显降低，二次谐波非线性系数增加，β与微裂纹的深度呈正相关(见图7)，这与KAWASHIMA等[15]在对微小表面裂纹产生的非线性响应的有限元模拟与试验中得出的规律相似。产生这种现象的原因是当微裂纹深度增加时，裂纹边界接触面积增加，张开与闭合效果增强，从而导致非线性响应增强。

图7 模拟得到的微裂纹深度与非线性系数的关系曲线

2.2 恒应力作用下微裂纹宽度对非线性表面波传播行为的影响

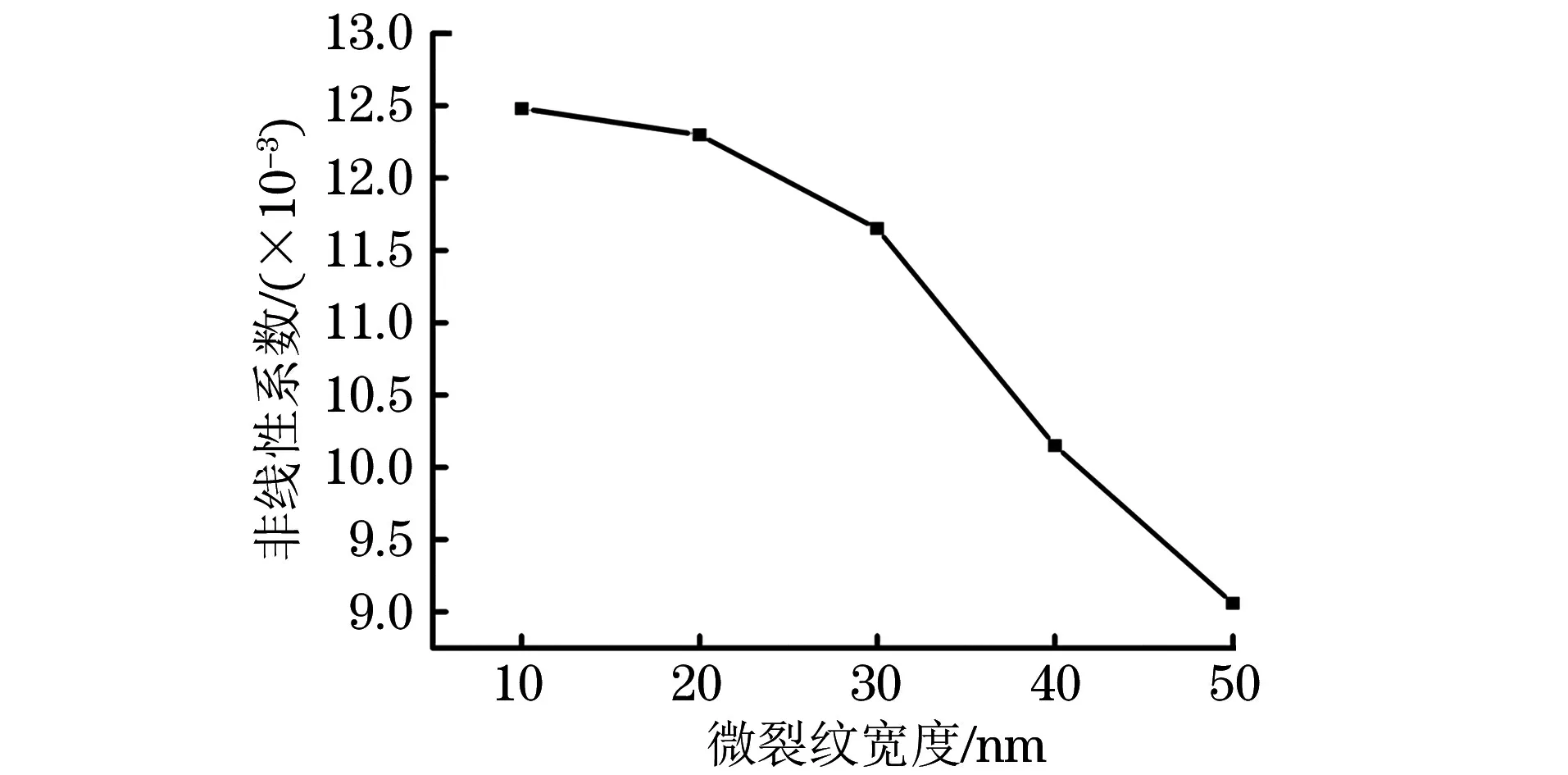
图8 模拟得到的微裂纹宽度与非线性系数的关系曲线

固定微裂纹宽度为0.3 mm，拉应力为1 MPa，分别选取宽度为10，20，30，40，50 nm的微裂纹进行模拟计算，发现随着微裂纹宽度的增加，二次谐波非线性系数减小，非线性系数与微裂纹的宽度呈负相关(见图8)，这与JIAO等[16]利用非线性兰姆波检测板中微裂纹的有限元仿真中得到的规律相似。产生这种现象的原因是随着微裂纹宽度的增加，表面波经过微裂纹时的衰减增加，微裂纹的周期性张开与闭合状态减弱，使得非线性响应也随之减小。

3 试验方法与结果

3.1 试样的制备

试样的尺寸及自制应力腐蚀平台如图9所示。

图9 试样尺寸及自制应力腐蚀平台示意

首先，将试样保存在温度为1 050 ℃的环境下30 min，使用砂纸、抛光膏对其进行打磨抛光后擦拭干净。选择试样表面半径为1 mm的圆形区域腐蚀5，10，15 h，选用质量分数为10%的FeCl3溶液作为腐蚀液，同时使用西安力创公司的应力环，将124 MPa的恒应力换算成应力环的变形量，对装有腐蚀装置的试样进行加载。

3.2 试验结果与分析

清洗试样后，利用OLS4000三维激光扫描共聚焦显微镜对3个时间段腐蚀完成后的试样表面进行观察，发现随着腐蚀时间的增加，腐蚀坑明显变大，将经过10，15 h腐蚀的试样放大100倍，发现蚀坑边缘逐渐有微裂纹产生(见图10)，测量其蚀坑尺寸，结果如图11所示。

图10 腐蚀试样形貌及局部放大图

图11 不同腐蚀时间的蚀坑尺寸

图12 试验和模拟得到的归一化非线性系数与腐蚀时间相关性

最后，利用美国RITEC公司的RAM-5000 SNAP非线性高能超声测试系统对不同腐蚀时间的试样分别进行检测，分析系统接收的响应信号，得到的归一化非线性系数与腐蚀时间相关性如图12(a)所示。利用有限元模型进行模拟时，由于试验过程中探头所发射的声束具有一定宽度，声波通过蚀坑处的尺寸不一致，为使模拟条件与试验条件更加贴近，分别选择蚀坑最大宽度、最大宽度的1/1 000和1/10 000进行模拟，将试验得到的蚀坑尺寸按照以上方法计算后代入到有限元模型中，将得到的信号进行叠加后分析，得到的归一化非线性系数与腐蚀时间相关性如图12(b)所示。结果表明：随着腐蚀时间的增加，试验测得的归一化非线性系数增加，这是由于随着蚀坑尺寸的增加，蚀坑边缘处微裂纹的张开与闭合状态增强；模拟得到的归一化非线性系数与试验测得的归一化非线性系数随腐蚀时间的变化趋势具有良好的一致性。由此验证，建立的非线性表面波检测应力腐蚀微裂纹损伤模型是切实有效的。

4 结语

(1) 恒应力作用下，微裂纹宽度与非线性系数呈负相关,其深度与非线性系数呈正相关。

(2) 拉应力作用下，裂纹开口变大，裂纹边界的周期性张开与闭合状态减弱，抑制了高次谐波的产生，压应力作用促进高次谐波的产生。

(3) 模拟得到的非线性系数与试验测得的非线性系数变化趋势具有良好的一致性。