半捷联式单反镜转台抗干扰性能研究

岑远遥 ，张立中 ，白杨杨 ，孟立新 ，张乐仪

（1.长春理工大学 机电工程学院，长春 130022；2.长春理工大学 空地激光通信国防重点实验室，长春 130022）

目前，对激光通信技术的研究主要是点对点通信形式，但点对点通信不能满足大容量、高速率的通信要求[1-3]。空间激光通信组网的方式则能实现信息传输的高效率、保密性及可靠性，因此组网的通信方式是激光通信技术的一个主要发展方向[4-6]。单反镜转台作为组网的从光端机，为保证组网系统的跟踪精度，需要对伺服系统的控制策略进行设计。

单反镜转台的主要作用是隔离载体的扰动，保证光学天线在惯性空间中的视轴指向精度[7-8]，从而实现对目标的稳定跟踪。传统的稳定方式是陀螺稳定，也称直接稳定，即将陀螺直接安装在方位与俯仰框架上。随着对稳定平台的小型化、轻量化与低成本的要求提高，直接稳定的方式难以满足稳定平台轻小型化的要求。

半捷联稳定控制[9]的提出，使得这一问题得到了较好的解决，半捷联稳定平台是一种数字稳定平台[10]，即将惯性传感器直接安装在稳定平台的基座上，通过复杂的数学解算得到方位与俯仰框架的角速度指令[11]。

对半捷联式单反镜跟瞄转台的控制进行研究。首先，介绍直接稳定与半捷联稳定的控制原理，然后对单反镜转台载体与框架之间的角速度耦合关系，运用角速度补偿算法进行解耦；对影响稳定平台的稳定精度的因素进行分析，并提出相应的解决策略，最终结合MATLAB仿真与实验，验证设计的控制策略对系统稳定精度提高的有效性。

1 稳定平台稳定机理

1.1 直接稳定平台稳定原理

直接稳定方式是将两个高精度角速率陀螺作为稳定回路的惯性传感器，其稳定方式具有较大的带宽以及精度，因此被广泛应用于机载、车载等稳定平台上。如图1所示为角速率陀螺稳定的控制原理。

图1 直接稳定方案控制原理

其中，uz为速度环指令信号；ϑ̇为姿态扰动信号；ug为角速度反馈信息；ωp为平台输出角速度信号；Gp(s)为稳定平台伺服传递函数；Gg(s)为速率陀螺传递函数。

由图1可知，陀螺稳定回路是一个速度控制系统，其稳定精度受到速度环指令信号uz与载体姿态扰动ϑ̇的影响，稳定平台在惯性空间中的角速度为：

通过式（1）可知，速率陀螺稳定方式通过高增益速度回路实现视轴在惯性空间中的稳定。

1.2 半捷联稳定

对半捷联稳定方式而言，单反镜转台将惯性传感器直接安装在系统基座上，实现系统的低成本与轻量化。而系统的视轴稳定是通过半捷联惯性测量单元提供的，载体姿态信息通过数学解算实现，半捷联属于一种带有前馈稳定的复合控制方式。半捷联稳定控制原理如图2所示。

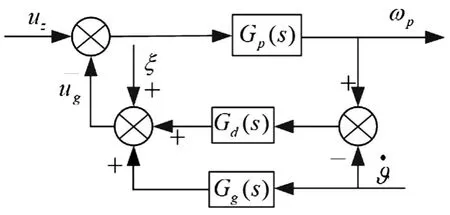
图2 半捷联稳定控制原理

图2中，uz为角速度指令信号；ϑ̇为姿态扰动信号；ug为角速度反馈信息；ωp为平台输出角速度信号；Gp(s)为稳定平台伺服传递函数；Gg(s)为速率陀螺传递函数；Gd(s)为测速环节传递函数。由半捷联稳定原理可以得到：

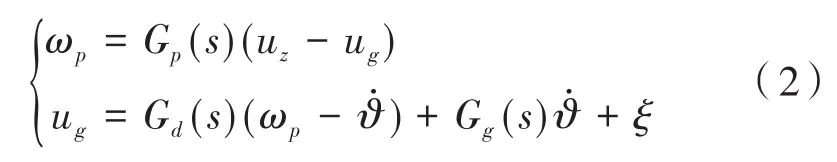
通过式（2）可以得到单反镜输出角速度为：

2 半捷联稳定平台的稳定方法

2.1 单反镜平台解耦方案

在稳定状态下，捷联稳定平台可以通过稳定视轴在惯性空间的指向来实现对载体扰动的解耦[12]，如图3所示为半捷联稳定解耦原理框图。通过对单反镜稳定平台进行研究，角速度补偿算法实质上是一种直接稳定方式的演变，该方式是利用陀螺测量的角速度进行融合后得到补偿指令，角速度补偿方法比角位置补偿方法易于实现，测角范围广，易于补偿。而角位置补偿算法是通过位置闭环的稳定方式，能够避免因微分测速带来的问题，但是由于存在积分的问题，在实际系统中，会产生误差的累计，为降低误差累计的影响，需要使用精度更高的惯性测量单元，同时该算法也较为复杂。因此利用角速度补偿算法对半捷联式单反镜进行解耦，使用光电编码器作为角位置测量传感器。

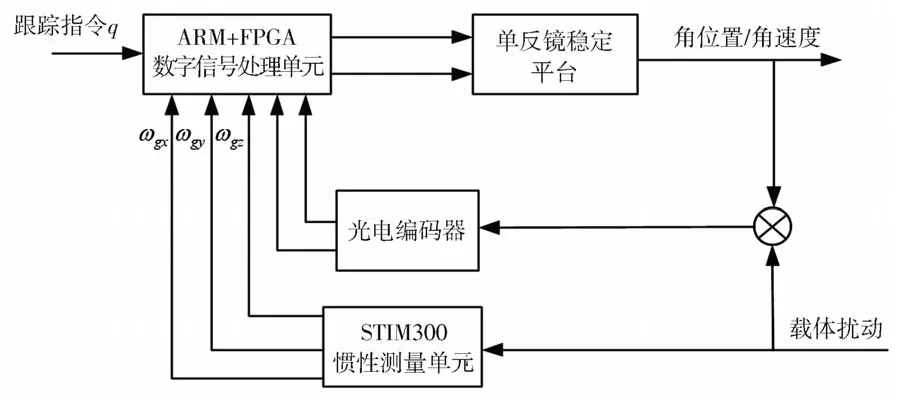
图3 半捷联稳定解耦原理框图

2.2 角速度补偿下半捷联解耦方法

方位框架与载体坐标系之间的姿态变换矩阵为：

图4 角速度补偿稳定原理

图5 视线坐标系与载体坐标系之间的变换关系

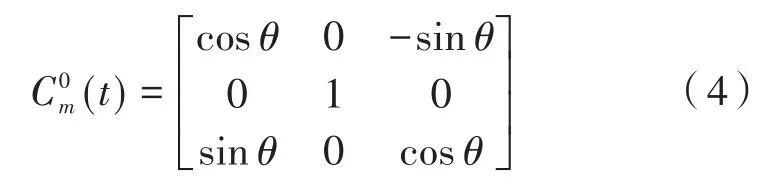
俯仰框架与方位框架之间的姿态变换矩阵为：

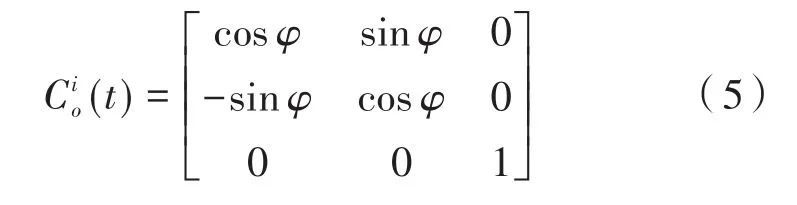
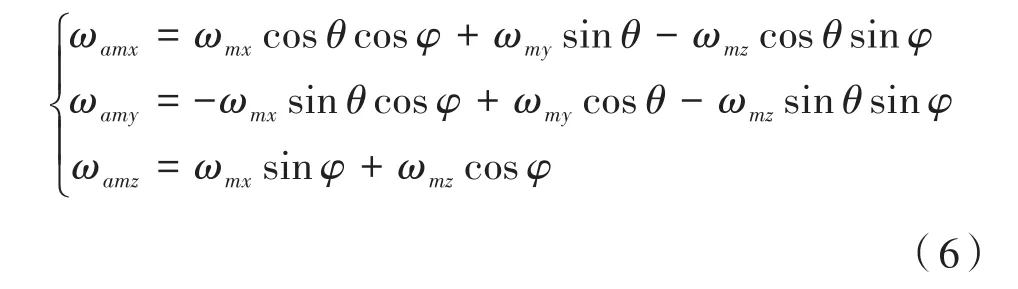
根据姿态变换矩阵可知，单反镜载体对视轴的耦合角速度在单反镜坐标系上的分量如式（6）所示。当在跟踪状态下，视轴指向将受到方位与俯仰框架的角速度的耦合，其视线坐标的角速度分量为：

通过上述两式整合，可得单反镜转台视轴在惯性空间中的角速度为：

在稳定状态下，视轴在惯性空间中的角速度ωax=ωay=ωaz=0，所以对半捷联稳定平台有：

由公式（7）和公式（9）可以得到方位和俯仰框架的实时补偿指令为：

角速度补偿的方式解耦方案，其结构简单，计算量相比角位置解耦的计算量小很多，惯性元件只需提供载体的俯仰角速度、方位角速度与滚转角速度。

3 稳定平台视轴稳定技术

3.1 载体扰动对系统的影响

为保证单反镜跟瞄转台的视轴在惯性空间中的稳定，必须隔离载体的扰动对跟瞄系统的影响，因此能否隔离载体扰动是半捷联稳定方案实施的前提。

载体的姿态扰动如下：

式中，ϑ̇m为扰动角速度幅值；fm（t）为扰动角速度频率。

为了便于分析系统的耦合作用，假设系统的角速度输入指令uz=0以及系统噪声ξ=0，通过式（3）可以得到单反镜跟瞄系统视轴输出角速度为：

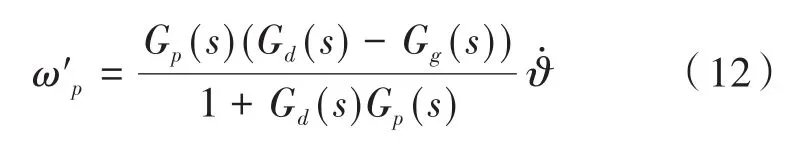
需要隔离载体扰动引起的方位框架与俯仰框架的运动，则ω'p=0，结合式（3）与式（12）可以得到理想条件下，半捷联转台实现完全解耦的条件为Gd(s)=Gg(s)。即实现陀螺传递函数与测速环节传递函数完全匹配。而实际情况下，测速环节的动态性能要优于捷联惯性单元的动态性能。

为使捷联惯性单元与测速环节能够匹配，可以有以下三种方法实现：（1）对测速环节进行滤波或选择高性能的陀螺；（2）对测速环节进行匹配滤波的方法实现测速环节与捷联单元的动态性能匹配；（3）选择带宽介于陀螺与测速环节之间的传递函数，并通过采取折中的方法进行校正后匹配中间值。上述三种方法中，第一种方法会放大系统的测量噪声，选择高精度陀螺则会增加系统成本；第三种方法则比较复杂，因此选择第二种方法实现半捷联稳定。

3.2 匹配滤波器设计

因采用角速度补偿算法解耦后，为消除载体扰动对稳定平台视轴的影响，根据前文分析，通过匹配微分测速通道与捷联惯性单元测量的载体扰动的动态特性[13]。应用不变性原理，对测速环节的Gd(s)进行匹配。滤波器形式一般如下：

通过图4简化得到图5所示的控制框图，如两幅图所示，其中Gg(s)为捷联角速率陀螺传递函数，Gd(s)为测速环节传递函数；G1(s)表示角速率补偿及稳定平台传递函数，Gm(s)为匹配滤波器传递函数。

通过图6可以得到，稳定平台角速度输出函数为（14）。

图6 简化后的捷联控制框图

其中，G1(s)=GJ(s)Gv(s)。

为验证匹配滤波在半捷联稳定平台控制中的有效性，对其进行仿真分析。通过采用扫频法，得到系统被控对象与陀螺传递函数，系统相关参数如下：

根据有约束非线性最小化方法[13]，如图7选为T1=0，T2=0.003～0.005时的匹配程度，增大T2时系统的解耦精度增加。

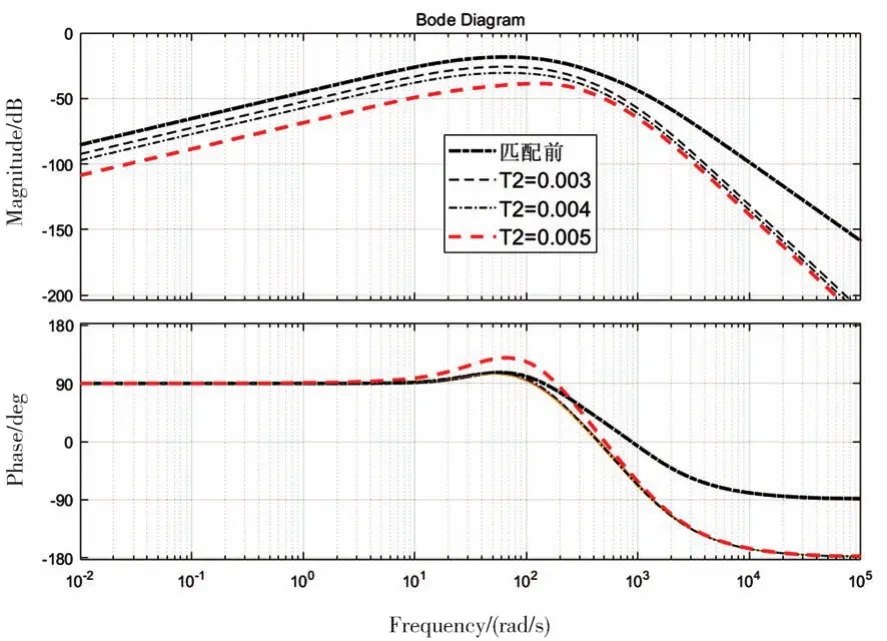
图7 T2变化时对系统的匹配程度的影响

如图8所示，根据前面当选择T2=0.005时为最佳，T1=0～0.002变化时，随着T1的增大，系统的解耦精度降低。通过图中可以得到当T1=0，T2=0.005时效果最优，如图9所示，系统的解耦精度在1 Hz时提高了28 dB。

图8 T1变化时对系统匹配程度的影响

图9 匹配前后幅频特性曲线

在不考虑干扰力矩与系统噪声的情况下，系统在幅值为3°，频率为1 Hz的扰动下，系统匹配前后的误差如图10所示。在加入匹配滤波器后系统的稳定精度从均方误差0.093 3°/s（1σ）提升至0.108 7°/s（1σ）其稳定精度提高了88.3%，匹配滤波器能够有效地抑制载体扰动对系统稳定的影响。当系统引入测速噪声与扰动力矩的情况下，系统的稳定精度明显降低，其稳定误差增大。如图11所示，引入测速噪声与扰动力矩后系统的稳定精度明显降低[14]，所以为了使稳定平台达到一定的稳定精度，必须要抵消一部分或有效地减小扰动力矩对系统的影响。

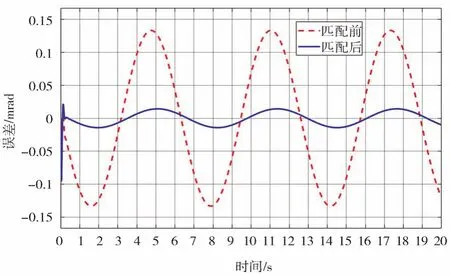
图10 系统匹配前后稳定误差对比

图11 引入扰动力矩后系统的稳定精度

3.3 扰动观测器设计

根据前面的仿真分析，为了提高半捷联的稳定精度，采用扰动观测器（DOB）[15-16]来抑制扰动力矩与测速噪声对稳定精度的影响。扰动观测器原理如图12所示。

图12 扰动观测器原理

根据扰动观测器的原理，平台扰动力矩到平台的角速度的输出传递函数为：

在半捷联单反镜稳定平台中，干扰观测器原理如图13所示。

图13 半捷联稳定平台中干扰观测器原理

扰动观测器的设计主要考虑的是低通滤波器的设计，在剪切频率满足|Q(jω)|≈1时系统低频的扰动会被抑制，半捷联稳定平台工作在低频段，因此其低频扰动被抑制后，系统的稳定精度将会提高。

结合系统带宽的影响（设计带宽大于20 Hz），通过仿真与实验的实际验证，干扰观测器中参数T=0.004时能够满足系统的带宽，同时系统具有较好的跟踪精度。因此设计的扰动观测器的低通滤波器为：

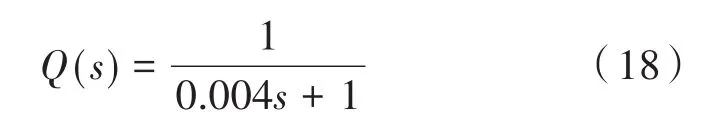
在不考虑系统微分测速产生的噪声时，给系统施加扰动。匹配滤波与干扰观测器Simulink仿真如图14所示，加入扰动观测器后系统仿真的稳定误差对比如图15所示。加入扰动观测器后，稳定精度的误差从 0.520 5°/s（1σ）提升至0.010 91°/s（1σ）系统的稳定精度提高了79.03%，在很大程度上抑制了扰动力矩对系统稳定精度的影响。

图14 匹配滤波与干扰观测器Simulink仿真

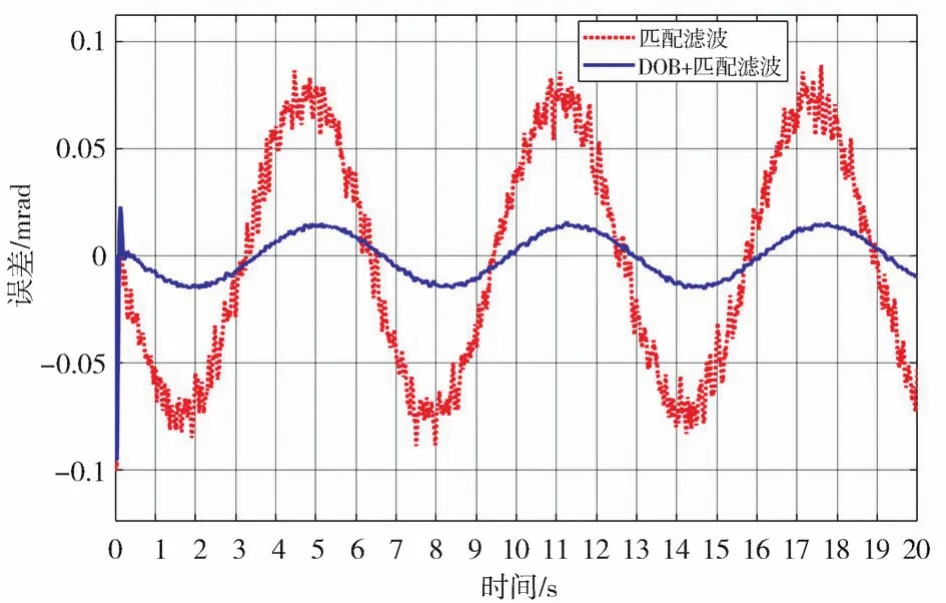
图15 加入扰动观测器前后系统稳定精度对比

4 单反镜跟瞄系统稳定性实验

如图16所示，实验装置分为发射和接收两部分，发射端使用靶标作为模拟目标源，通过模拟主光端机的运动，其由激光器（波长为830 nm）、平行光管、反射镜以及靶标控制器组成。接收端为单反镜跟瞄转台置于三轴摇摆台上，模拟飞机运动时的姿态，其由光学天线、CCD相机、粗跟踪伺服控制系统以及上位机组成。

图16 单反镜转台粗跟踪控制实验

接收端光学天线中的反射镜作为独立单元，其粗跟踪相机探测视场为4 mrad，CCD相机的像元角分辨率为4 μrad，帧频为100 Hz。采用STM32与FPGA作为从光端机的控制器件，通过FPGA采集陀螺的相关数据并完成数学解算后发送至STM32控制器。

对扰动观测器Q（s）、测速环节Gd(s)进行离散化处理，扰动观测器通过低通滤波器和控制对象数学模型的逆估计出系统的外部扰动，同时将扰动估计信号补偿至控制的输入，在捷联稳定回路中引入等效的补偿，最终实现对转台扰动的抑制。通过编程实现数字化控制，上位机软件使用Labview软件进行编写，所有子单元与粗跟踪伺服系统相连，采用422串口通信，并由上位机统一控制。

通过三轴摇摆台对单反镜转台施加幅值为2°、频率为1 Hz的正弦扰动，对靶标施加幅值为0.5°、频率为0.5 Hz的正弦扰动。如图17所示，在采用传统PID控制下系统方位轴的跟踪均方误差为 42.37 μrad（1σ），如图18所示，采用匹配滤波与DOB控制下系统方位轴跟踪均方误差为12.69 μrad（1σ），实验表明在采用匹配滤波与扰动观测器后系统动态跟踪精度得到了有效提升。

图17 在传统控制下系统方位框架跟踪误差

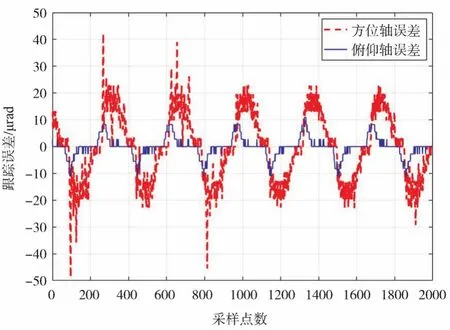
图18 在匹配滤波与DOB控制下系统跟踪误差

5 结论

在分析直接稳定与半捷联稳定方式后，对半捷联式单反镜跟瞄转台光栅测速与惯性元件测速的耦合惯性进行分析，采用角速度补偿算法对其进行解耦。对半捷联稳定精度的影响因素进行分析，同时提出了相应的解决方案。通过仿真结果表明在采用匹配滤波器后，稳定平台的解耦精度在1 Hz时提高了28 dB，系统的精度提高了88.34%。最后根据系统的组成原理，搭建了相应的实验平台，对理论仿真进行实验验证，在未采用匹配滤波与扰动观测器下，直接使用传统的PID控制系统的跟踪均方误差为42.37 μrad（1σ），采用匹配滤波同时加入扰动观测器后系统的跟踪均方误差为 12.69 μrad（1σ），系统的跟踪精度提高了70.05%。实验结果表明匹配滤波与扰动观测器后对半捷联稳定平台系统的精度得到了有效提升。