基于ASRUKF的锂离子电池SOC估算

徐劲力，郎锦峰，徐 维，刘佳俊

(武汉理工大学机电工程学院，湖北武汉 430070)

电池荷电状态(SOC)估算能够实时显示电池剩余电量的状况，是保障电池正常工作的基础[1]。

离线和在线辨识是等效电路模型参数辨识的主要方法，前者得到的模型参数无法反映电池实时的动态特性，后者通过实时采集可测变量，模型参数辨识结果更为准确。递推最小二乘法具有计算简单、容易实现等特点，是在线辨识中应用较多的方法之一[2-4]，然而由于递推关系和数据量的增加，旧数据也一直影响着新输入数据的递推结果。

在电池SOC估算方面，初值准确与否对安时积分法估算SOC影响很大，容易造成误差累积[5]；需要长时间的静置使得开路电压法在线估算变得不方便[6]；内阻法则受电池种类和数量等的影响，在实际中应用很少[7]。后来智能算法也被用来进行SOC估算，通过对大量的测量数据进行训练和学习从而进行预测，典型的有支持向量机[8]、神经网络[9]等，这类算法不依赖数学模型，但对数据集的质量和完整度有较高的要求。目前基于模型的估算方法中卡尔曼滤波(KF)算法最为常见，无迹卡尔曼滤波(UKF)算法使用无损变换，且避免求解雅可比矩阵，减小了非线性误差[10]，精度比扩展卡尔曼滤波(EKF)更高，但容易带来协方差矩阵非正定的情况。

为了解决最小二乘法在参数辨识过程中出现“数据饱和”的情况，以及无迹卡尔曼滤波易出现协方差矩阵非正定的情况，本文在Thevenin 模型的基础上，参数采用限定记忆最小二乘法辨识，电池SOC采用自适应平方根无迹卡尔曼滤波算法(ASRUKF)进行估算。

1 电池模型的建立

等效电路模型通过电路元件的组合来模拟电池特性，利用数学方法来建立不同参数之间的关系。图1 为一阶RC 电路模型，即Thevenin 等效电路模型，内部动态特性通过阻容网络来模拟。欧姆电阻用R0表示；开路电压为UOCV；用R1和C1分别表示极化电阻和电容；端电压为Ut；U1为RC 回路的极化电压；I为电流，充电时电流为正，放电时电流为负。

图1 一阶RC 电路模型

根据所建模型和电压定律，可建立如下电路方程：

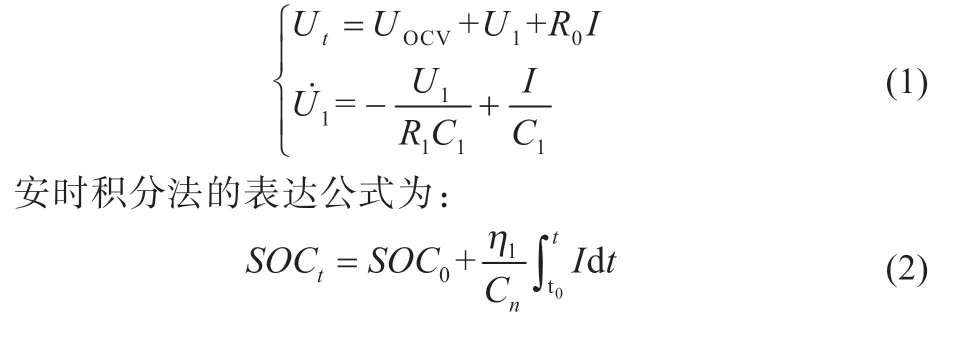
式中：SOC0为初始SOC值；η1为充放电效率，通常取1；容量用Cn表示；t0和t分别代表初始时刻和t时刻。

离散化处理之后，状态空间方程如下：

式中：T为采样时间；w为过程噪声；v为测量噪声，是用来模拟不确定性的高斯白噪声，状态变量为xk=[SOCk，U1,k]，控制变量为uk=Ik,，观测变量为yk=Ut,k。

2 实验平台建立

本次实验采用如图2 所示的电池测试平台，主要包括测试系统、恒温箱、电池、数据采集设备等，三元锂电池具体参数为：温度为25 ℃，标称容量2.5 Ah，充电截止电压4.2 V，放电截止电压2.75 V。

图2 电池测试平台

通过对电池的充放电测试，得到电池开路电压的测试数据。为了能够更好地反映电池OCV和SOC的关系，本文通过九阶多项式来拟合OCV和SOC的关系曲线。由于迟滞效应，同一SOC值情况下，充电曲线和放电曲线之间存在电压差值，因此采用取平均值的方法来进行曲线拟合，曲线如图3 所示。

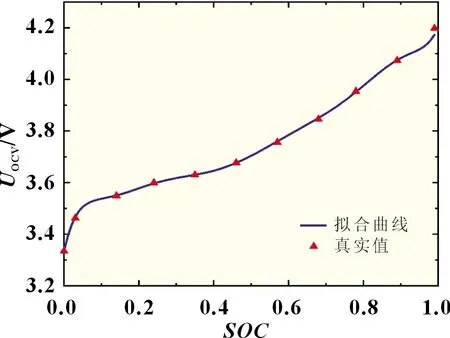
图3 OCV-SOC拟合曲线

拟合曲线的评价参数RMSE为0.002 128，表明该曲线有较好的拟合效果。

3 参数辨识

3.1 限定记忆最小二乘法

针对等效电路模型的参数辨识，最常用的是递推最小二乘法，但在递推算法的过程中，随着递推次数和数据量的增加，在增加新数据的同时，旧数据一直影响着新数据的递推结果。因此，针对上述存在的问题，提出了限定记忆最小二乘法来进行参数辨识。

这种方法在增加新数据的同时，剔除旧数据，依赖有限个最新数据来进行参数估计，记忆长度L始终保持不变，这样能够有效解决“数据饱和”带来的问题[11]。

下面是限定记忆最小二乘法的递推原理：

式中：h(k)为数据向量；z(k)为输出量；θ 为参数向量。递推公式如下：

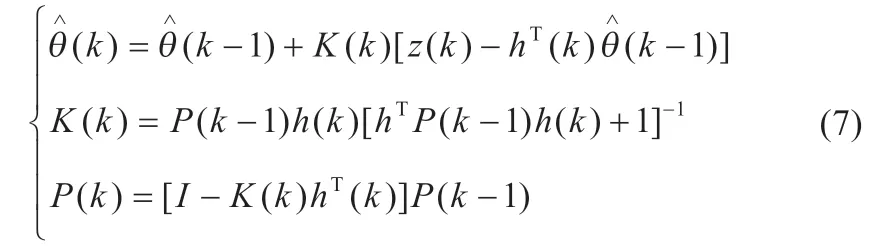
在递推初始时刻，需要对部分参数赋予初始值，通过递推更新来对参数进行预测，其基本思想可用图4 来表示。

图4 限定记忆最小二乘法递推示意图

假设当前时刻为k，则根据上一时刻的参数值协方差、参数估计值以及增益可以递推得到当前时刻的估算值，此时，需对记忆区间内的数据进行增删更新，从而计算得到k+1 时刻的参数值。

结合模型辨识的精度以及辨识所用时间，参数辨识所选取的记忆长度为200。

3.2 电池模型参数辨识

根据所建立的等效电路模型可得到如下所示的函数：

将z(k+1)=hT(k)θ(k+1)+ν(k)以及h(k)和θ(k)代入限定记忆最小二乘法中进行参数辨识，进而可以求得电池模型对应参数的值。

3.3 辨识模型的验证

为了验证模型参数辨识的准确性，将辨识的模型参数带入端电压的求解公式中，可以得到端电压的仿真值，将仿真值与实测值进行对比。通过上述实验平台模拟城市道路循环工况(UDDS)，得到电压和电流数据。将模型的参数辨识结果代入，模型的端电压仿真值和实测值结果如图5 所示。图6为模型端电压的误差。

图5 端电压仿真值与实测值

图6 模型端电压误差

从图中可以看到，所建立模型参数辨识的整体精度较好，采用限定记忆最小二乘法LMRLS 辨识的模型端电压仿真值和实测值的误差大部分保持在0.02 V 以内，在15 300 s 左右，电池SOC降至10%，此时，模型的非线性增大导致端电压误差开始增大，最大为0.07 V；而最小二乘法RLS 辨识的模型端电压仿真值和实测值误差保持在0.04 V 以内，最大误差达到0.08 V，前者的模型端电压的均方根误差RMSE为0.014 5，后者为0.0176，因此LMRLS 比RLS有更高的参数辨识精度。

4 SOC 估算

4.1 算法的建立

无迹卡尔曼滤波(UKF)采用无损变换，其原理是利用概率密度分布近似的方法来处理非线性函数，其精度可达泰勒展开式的第三阶。针对在误差协方差迭代过程中易出现矩阵非正定问题，本文将协方差用协方差阵的平方根进行迭代，并结合自适应滤波器来进行SOC的估算。

平方根通过QR 分解和Cholesky 一阶更新来获得[12]，自适应滤波器对迭代过程中的噪声更新，避免噪声不准确对估算结果的影响。

ASRUKF 的估算过程如下[13]：

(1)状态函数初始化：

(2)构建Sigma 点：

(3)时间更新，对构建的Sigma 点进行状态方程的处理，预测系统状态量和误差方差矩阵：

(4)对Sigma 点进行重采样：

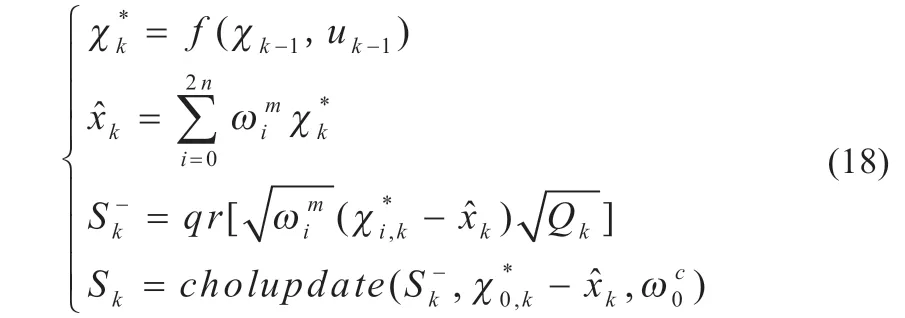
式中：dk=(1-b)/(1-bk+1)，遗忘因子b介于0 到1 之间，这里取0.95。

对方差矩阵和误差协方差进行更新：

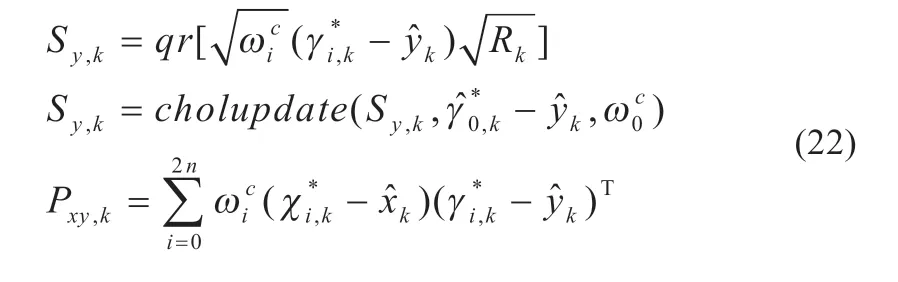
(5)计算增益矩阵，并对估计量和方差进行更新：

根据限定记忆最小二乘法辨识的结果，代入公式(3)和(4)，可完成SOC的估算。

4.2 估算结果的分析

为了验证上述算法的准确性，将UDDS 工况的电流作为输入，初始SOC值均设置为0.7。图7 为UKF 和ASRUKF 估计结果与参考值的对比图。图8 为两种算法的估算结果与参考值的误差曲线。

图7 UDDS工况下的SOC估算结果

图8 UDDS 工况下的估算误差曲线

从图7 和图8 可以看出，UKF 和ASRUKF 两种算法都能够比较快速地收敛到真实值附近，但是ASRUKF 相比UKF 有更好的估算结果。UKF 算法估算误差大部分都在2%以下，最大误差为4%，出现在SOC低于10%的时候，这是由于放电末段非线性增强导致；在SOC大于10%的时候，ASRUKF 的估算误差均小于1%，在SOC小于10%的时候误差增大，但是最大误差也小于2%，不同算法的估计误差如表1 所示。

表1 不同算法的估计误差 %

与UKF 算法相比，ASRUKF 算法确保估算结果收敛，避免因干扰和计算误差而导致协方差矩阵非正定，也减少了计算量，同时加入自适应算法使得状态估计过程中能够实时进行噪声更新，提升了估算结果的准确性。

5 结论

在Thevenin 等效电路模型的基础上，针对最小二乘法在参数辨识过程中存在“数据饱和”的问题，模型参数采用限定记忆最小二乘法进行辨识，利用固定记忆长度的数据来减小旧数据累积对结果的影响，并通过工况端电压来验证模型辨识结果的准确性。采用自适应平方根无迹卡尔曼滤波来进行SOC估算，并与UKF 结果的对比分析，证明该方法有更高的估计精度。