基于GLD电池模型和FFRLS-EKF算法的SOC估测

栗欢欢，孙化阳，陈 彪，王亚平

(1.江苏大学汽车工程研究院，江苏镇江 212013；2.江苏大学材料科学与工程学院，江苏镇江 212013)

锂离子电池因具有能量密度高、循环寿命长、自放电率低等优点而成为当前一种主流的二次电池产品，并广泛应用于新能源汽车、储能电站等领域。据MarketsandMarkets 发布的报告显示，到2025 年全球锂离子电池市场复合年增长率将达到15%[1]。

锂离子电池的SOC表征当前电池内部的剩余电量，电池管理系统通常以此为依据对动力电池进行优化控制[2]。不准确的SOC估算会极大限制电池其他方面的管理，因此对SOC进行精确估算是学界一个重要研究方向。

目前基于模型的SOC估算方法[3-4]主要分为两大类，一类是基于等效电路模型，该模型从电池的外部特性入手，采用电阻电容来模拟电池复杂的内阻情况。等效电路模型通过多年的发展，其模型精度获得了极大的提升，但是其模型精度是靠计算复杂度换取的。目前等效电路模型中，二阶RC电路是公认较为折中的一种模型。与等效电路模型不同的是，一些学者选择从电池内部着手[5-6]，通过对电池内部复杂的化学反应进行建模以获得更加真实的锂离子电池电化学模型。电化学模型通过详细且复杂的电化学偏微分方程描述了电池内部反应机理，因此其精度相对较高，但其计算是一个极大的挑战，因此在电化学模型的发展道路上，对模型的简化是学者们最为关心的焦点。

近日，针对锂离子电池SOC估算，有学者提出一种基于气液动力学原理的气液动力学锂离子电池模型(gas-liquid dynamic battery model,GLD)[7-9]。文献[7]和[9]从机理上报道该模型能够仿真电池中锂离子扩散与平衡等过程。文献[8]基于气液动力学模型提出了一种强鲁棒性的SOC估算方法，但该文献在一定程度上降低了气液动力学模型对电池温度效应的仿真能力。气液动力学模型的状态方程与等效电路模型相比能够直接反应温度对系统的影响，且其自迭代的特性使得其对异常输入具有较强的鲁棒性。然而，原始的气液动力学电池模型在工况突变时模型精度会有较大下降，且模型参数固定，存在随电池使用产生误差扩大的现象。

为解决上述问题，本文在气液动力学模型的基础上应用含遗忘因子的递推最小二乘算法(forgetting factor recursive least square method,FFRLS)以改进原始模型因参数无法自适应而产生的估算误差扩大问题，此外为保证FFRLS 算法的效果，选择扩展卡尔曼滤波算法(extended Kalman filter，EKF)，实现FFRLS 和EKF 的联合仿真，提高了模型的准确度和算法的估算进度。

1 气液动力学电池模型建立

电池内部是一个非常复杂的非线性系统，存在欧姆极化、浓差极化和电化学极化。欧姆极化是由欧姆内阻引起的，电化学极化主要是由电化学反应存在迟滞性造成的，而浓差极化则是由于电解液中锂离子浓度扩散的滞后性导致的电极表面与电解液内存在浓度差而产生的。通过Bazant和Liang 等[10-11]的研究可以发现，锂离子的扩散行为是研究端电压滞后开路电压的关键，掌握锂离子的扩散规律对电池SOC估算具有重要意义。

已有的研究[7,9,12]表明，电池系统内部锂离子扩散失衡与再平衡过程与气液系统存在以下相似性：

(1)气液系统内外存在的压力差和锂离子电池正负极之间的电位差都定量地描述了系统内部的势场；

(2)锂离子电池内部的欧姆极化特性与气液系统管道阻力的物理含义相同，且均为线性影响；

(3)锂离子电池停止工作，不再发生氧化还原反应后，其锂离子扩散消除浓度差异过程与气液系统关闭阀门后内部气液平衡扩散过程相似。

因此从流体力学角度，锂离子的扩散失衡以及再平衡过程为经典的扩散问题，可以尝试将电池模拟为气液系统，对其进行流体与扩散分析。

气液动力学模型如图1 所示。系统内部填充理想气体，部分理想气体溶解于液体内部。当阀门关闭时，系统与外界不存在任何物质能量交换，当阀门打开后，系统才与外界存在物质能量交换。

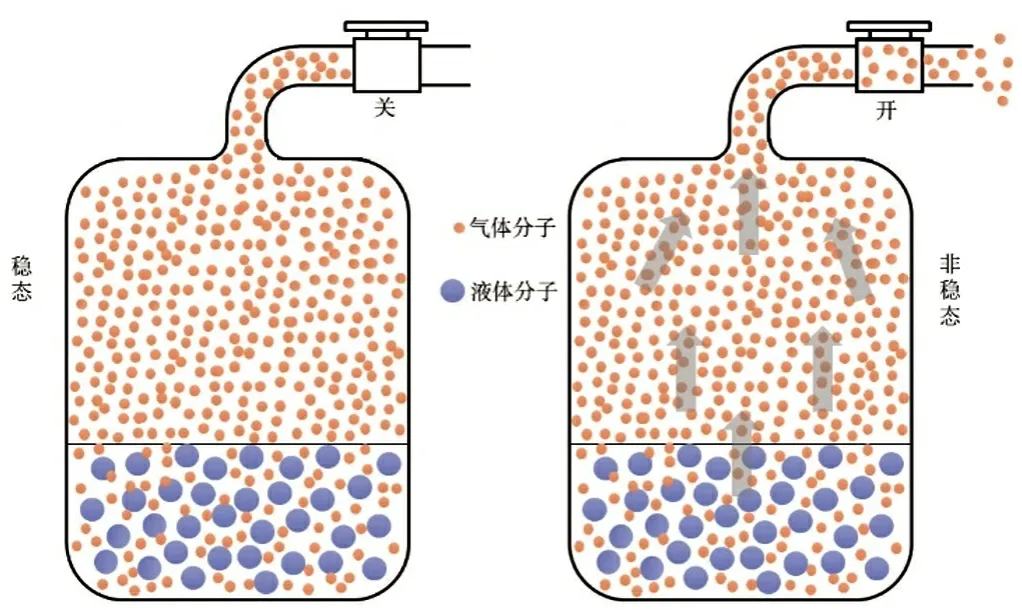
图1 气液系统示意图

由以上分析可知，在系统稳定的t1时刻，可写出此时的理想气体状态方程：

式中：Vl为系统内液体体积；nlg1为溶解于液体中的气体的物质的量；φm为气体分子的有效间隙；bm为气体分子的范德华体积。

此后阀门打开，对外释放气体，经过极短的时间Δt后，到达t2时刻，此时系统的热力学温度为T2，可以写出此时的理想气体状态方程，此外，根据伯努利方程，有：

式中：Pn,1为t2时刻阀门处压强；v为气体流速；μ 为管道阻力系数；ρ 为气体密度。

此时阀门关闭，气液系统与外界隔绝能量物质交换并开始再次平衡内部状态，假设在t3时刻，系统恢复平衡，由于系统与外界绝热，系统的热力学温度依然为T2，此时可以写出当前对应的理想气体状态方程和气体间隙填充度方程。

根据上述过程可知，从t2到t3时刻，从液体中析出的气体的物质的量为nlg2－nlg3，其中，nlg2为t2时刻溶解于液体中的理想气体的物质的量。而t1到t2时刻，由于Δt极小，可近似认为nlg2=nlg3，由于从t2到t3系统内部各物质总量未发生改变，故可建立nlg2、nlg3、n2－n3之间的关系，进一步代入理想气体状态方程和气体间隙填充度方程，可最终获得式(4)：

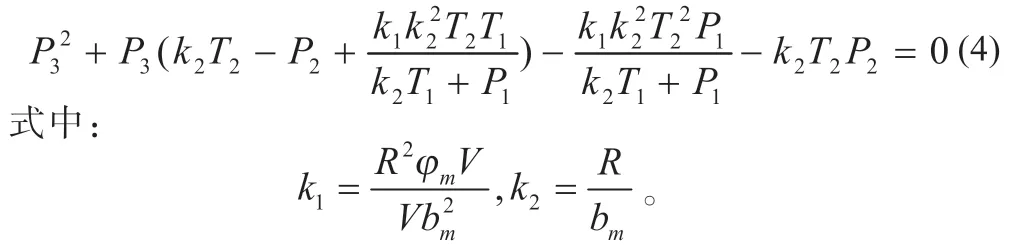
在实际的物理系统中，根据韦达定理，式(4)存在唯一正解。对充放气过程进行统一，定义充气为正，放气为负，则有：

在上式中，令k3=ρ/2，k4=μρ/2，可获得最终的气液动力学模型：

将其改写为电压电流形式，即：

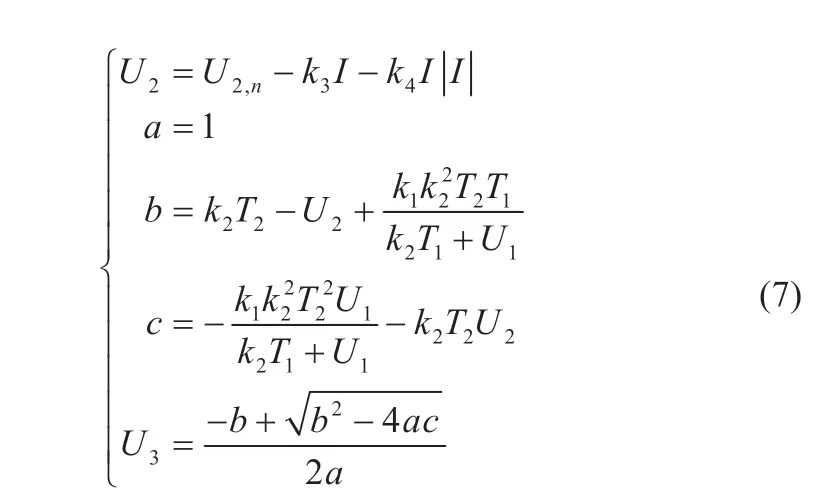
式中：U1为t1时刻电池开路电压；U2为t2时刻电池中间电压；U2,n为t2时刻电池端电压；U3为t2时刻电池开路电压。

由式(7)可看出，气液动力学模型结构简单，状态方程内无复杂计算，计算花费极小。与传统模型相比，气液动力学模型直接研究锂离子扩散的问题，更具有针对性。此外，气液模型在建模过程中，直接反应了温度对锂离子迁移扩散的影响，无需像等效电路模型一样引入温度系数。最后，气液动力学模型本身为具有马尔科夫性质的离散状态方程，当前时刻开路电压受上一时刻开路电压和当前输入电压共同影响，这使得气液动力学模型自身具有极强的抗干扰能力，且更易与传统优化算法结合，进一步提高模型精度。

2 基于FFRLS 的在线参数辨识

由于电池系统具有时变性，其内部参数会随着电池容量、循环次数、工作温度等发生变化，若不进行修正将造成模型估算误差的扩大。递推最小二乘算法可以实现模型参数的自我校正和更新，可以很好地克服电池系统因工作而造成的参数变化问题。

递推最小二乘算法以偏差平方和为基准进行寻优，通过不断输入最新的观测值以逼近当前模型参数的真值。传统最小二乘算法会将所有历史数据均纳入计算范围，然而对于持续变化的系统，传统最小二乘算法难以获得稳定且可靠的结果。因此，本文优选含遗忘因子的递推最小二乘算法(FFRLS)进行参数在线辨识。FFRLS 能有效克服传统递推最小二乘法存在的“数据饱和”问题，防止估计发散。

FFRLS 的基本计算方程如下：

含遗忘因子的递推最小二乘法的具体实现步骤如下：

3 基于FFRLS-EKF 的SOC 估计算法

电池系统在工作过程中是一个时变系统，对电池SOC的估算是一个不确定的信息。扩展卡尔曼滤波算法(EKF)是一种应用广泛的非线性滤波器，它可以减少由模型误差、传感器误差和系统累积误差等造成的估算误差。

3.1 扩展卡尔曼滤波算法

EKF 通过在每个时间步内对系统进行一阶泰勒展开来线性化非线性系统。首先，执行状态预测，获得当前系统状态的先验估计值，然后，执行状态更新，通过观测量修正先验估计值并进一步补偿由系统中各种噪声导致的各种误差。

当应用气液动力学模型时，电池的端电压可表示为：

EKF 应用于气液动力学模型时的详细步骤如下：

(1)初始化

对x0、P0、R0、Q0等进行初始化赋值。

(2)预测

(3)更新

式中：x为状态量初始值；P为估算误差协方差；Q为系统噪声；R为测量噪声；SOC及OCV为状态量；Ak为方程f()关于xk的雅可比矩阵；I为单位矩阵；zk+1为k+1 时刻电池端电压为k+1 时刻电池端电压的预测值。

按上述流程即可循环获得每个时刻的状态变量，并获得估算的SOC值。

3.2 FFRLS 和EKF 联合的SOC 估计算法

上述部分详述了FFRLS 和EKF 的实现步骤，为进一步提高模型精度，降低SOC估算误差，进行FFRLS 和EKF 的联合估计，实现下述效果：

(1)SOC的估算精度会影响FFRLS 的辨识结果，将EKF引入到辨识算法中，可为在线辨识提供更加准确的SOC值，降低模型误差，提高模型精确度。

(2) 模型参数直接影响SOC的估算精度，FFRLS 在每次估算循环中为EKF 算法提供更加准确的模型参数，提高算法的估算精度和鲁棒性。

根据上述分析，本文首先根据FFRLS 算法在线辨识模型参数k1、k2、k3、k4，接下来根据辨识的参数通过EKF 算法实现SOC估算，最后将估算的SOC值用于FFRLS 的参数辨识，实现整个系统的闭环修正，其流程如图2 所示。

图2 FFRLS及EKF 联合估算流程图

4 实验与分析

为了验证本文提出的FFRLS-EKF 联合估算算法的性能，选择了标称容量2 600 mAh，标称电压3.7 V 的商业电池，在恒定25 ℃下进行了恒流、混合动力脉冲能力特性(hybrid pulse power characteristic,HPPC) 测试和动态应力测试(dynamic stress test,DST)。测试设备为宁波拜特公司所提供的电池测试系统。待测电池和测试系统如图3 所示。

图3 (a)待测电池与(b)电池测试系统

4.1 SOC-OCV 曲线获取

由于不精确的状态观测会造成显著的观测误差，因此，首先应获得较精确的SOC-OCV曲线。本文对实验电池进行了标准HPPC 测试，以反映电池电压与容量的关系。选取其中的特征数据点进行拟合，得到拟合函数如式(19)(其中UOCV为OCV的值)：

本文选择5 阶多项式进行拟合，在保证拟合精度的基础上，避免了过拟合并降低了计算量。拟合曲线在全局均较好地与实验数据吻合，并弥补了因充放电对应的开路电压不一致造成的松弛效应。

4.2 误差分析

图4 为恒流0.2C、0.5C、1C以及DST 工况下原始模型、仅使用FFRLS 和使用FFRLS-EKF 联合估算的实验结果，各算法的最大估算误差见表1。

表1 最大SOC估算误差表 %

图4 恒流及DST工况实验值、原始模型、FFRLS及FFRLS+EKF测试结果

如图所示，原始模型的误差抖动较为剧烈，其估算误差最大达到4.88%。在引入FFRLS 后，原始模型的抖动现象得到显著改善，这表明FFRLS 有效地克服了原始算法的抖动问题，但依然存在部分误差扩大的现象，最大估算误差为3.22%。较为明显地，在恒流0.5C的测试中，单纯引入FFRLS 在估算的中后段造成了较大的误差扩散，这是由于系统估算的SOC误差较大而未能准确辨识模型参数造成的。当采用FFRLS+EKF 联合估计算法后，误差扩大现象得到了明显抑制，SOC的全局估算误差都较为平稳且较小，在恒流1C工况下最大估算误差仅为1.46%。

5 结论

本文提出了一种基于气液动力学锂离子电池模型的在线参数辨识及SOC估算算法。其核心内容为：采用带遗忘因子的递推最小二乘算法对模型参数进行实时调整，并采用扩展卡尔曼滤波算法进行SOC估算，以提高原始模型的估算精度。此外，对比并评估分析了单独采用FFRLS 和采用FFRLS-EKF 联合估计算法的估算性能。在DST 工况下，采用原始模型、FFRLS 优化、FFRLS-EKF 联合估计优化三种方式时误差分别是4.88%、2.84%、1.75%。结果表明，FFRLS 可以有效改善原始模型的波动问题并提高估算精度，采用FFRLSEKF 联合估计算法进行SOC估算后，估算效果获得了较大提高。此外，同一算法在动态工况与稳态工况下的估算表现差值分别为1.67%、0.84%、1.07%，表明气液动力学电池模型对电池工况敏感度低，在应用优化算法后，其全工况估算精度无显著差异，具有良好的应用价值。

综上所述，本文提出的算法能够高精度、高稳定地估算锂离子电池SOC。后续的工作包括在性能足够的嵌入式微控制器中应用上述算法。