基于谱熵梅尔积和改进VMD的轴承故障预警

马小平， 李博华， 蔡蔓利， 韩正化， 陈泽彭

(中国矿业大学 信息与控制工程学院，江苏，徐州 221116)

旋转机械广泛用于工业生产中，其运行状态对设备的效率和生产安全有着重要影响. 而轴承作为其重要部件，对轴承的监测，尤其是通过识别早期故障来减少轴承磨损、失效带来的严重影响，是机械故障处理中至关重要的技术[1]. 因此，对轴承运行状态的监测，特别是早期故障的预警，对设备安全和稳定生产有着重要意义.

传统的故障预警建立在故障形成之后，对故障信号进行特征提取、信号分类. 贾志明等[2]用局部均值法对EMD分解的故障信号特征指标进行处理，通过和阈值对比能有效识别早期故障；郑小霞等[3]用PSO算法优化VMD的分解个数和惩罚因子，能精确提取故障信号微弱特征. 但此类方法没有在故障信号出现初期对其进行捕捉，实时性较差. 对此，本文将语音分析领域中语音端点检测思想加以迁移，提取振动信号的谱熵梅尔积[4](product of spectral entropy and MFCC0, MFPH)特征，利用双门限法检测故障起始点，采集起始点后的振动信号为异常样本，提高模型可信度和泛化能力.

针对轴承故障信号非平稳性强、特征频率易重叠且难以准确提取的问题，采用变分模态分解[5]对信号进行处理. VMD将信号分解转变为约束优化问题，通过迭代求解分量最优的带宽和频率中心，有效抑制了模态混叠. 刘长良等[6]将VMD与SVD结合，提取轴承故障特征；刘尚坤等[7]用互信息对VMD进行改进，增强了早期轴承故障特征提取效果.

轴承发生故障时，振动信号会产生动力学突变. 分解后轴承信号仍会受到随机性运动参数的干扰而难以准确识别，很难完全发挥VMD的优势. 排列熵 (permutation entropy,PE)无需考虑时间序列的实际数值，基于概率对相邻样本进行对比，放大了一维时间序列中的微弱变化，对动力学突变行为更敏感[8]，且具有计算快、抗干扰能力强的优势. 郑近德等[9]将PE与LCD结合，有效提取了滚动轴承故障信号特征. 但PE算法对子序列的数值及变化有所忽略，且只考虑单一尺度上动力学突变行为，提取信息有限. 因此，AZIZ等[10]提出了多尺度加权排列熵(multiscale WPE, MWPE)，克服了WPE单一尺度的不足，在表征不同尺度下时间序列复杂性上更有优势，鲁棒性更强[11].

本文针对轴承故障预警实时性差，难以精准提取早期微弱故障等问题，利用MFPH检测故障起始点，结合VMD和MWPE在重构故障信号、突出故障特征上的优势，建立了轴承故障预警模型. 基于测试信号和实际信号进行分析，验证了本文方法的有效性.

1 基于MFPH的故障起始点检测

1.1 MFPH原理

梅尔频率倒谱系数[12](Mel frequency cepstrum coefficient, MFCC) 是在Mel标度频率域提取出来的倒谱参数，描述了人耳频率的非线性特性. MFPH结合了MFCC对短时间功率谱包络描述的准确性和抗噪能力，以及谱熵[13](spectral entropy, SE)对低频敏感的特性. 在噪声干扰的环境下，MFPH能区分振动信号正常段和故障段的频率成分，可作为轴承故障起始点检测的重要参数. 对信号x(t)，其MFPH计算过程如下.

对信号x(t)分帧加Hanning窗处理，对每帧振动信号xi(t)进行傅里叶变换并计算谱线能量

E(i,k)=|fft(xi(n))|2

(1)

对每帧信号的能量谱经过Mel滤波器组，求和得到能量S(i,m)

(2)

式中：M为滤波器数目；Hm(k)为第m个滤波器.

将每个Mel输出表示为ln[S(i,m)]，对其进行离散余弦变换，获取每帧MFCC

(3)

计算第i帧对应的谱熵SE(i)

(4)

式中：i为帧标号；N为帧长度；Pi(k)为归一化的谱概率密度.

为保持与MFCC0维度一致，将SE值同样剔除起始与末尾各2帧，则第i帧的MFPH计算公式为

M(i)=-mfcc0(i)SE(i)

(5)

1.2 双门限MFPH故障起始点检测

为了区分正常信号段和故障信号段，需要获取各段信号MFPH参数数值分布规律. 双门限法基于短时平均能量和短时平均过零率，可根据正常信号及故障信号的不同参数值，选择故障段高低门限值并确定故障段的起始点. 模糊C均值聚类[14](FCM)通过不断更新隶属度函数和聚类中心来获取类内最小误差，可对MFPH的门限值进行评估，避免产生故障点漏检的情况.

针对样本集X，有聚类中心集mj，则算法目标是使J值最小

(6)

式中：C为聚类簇数；N为样本数目；μj(xi)为xi关于j类的隶属度；b为模糊常数且b>1；mj为j类聚类中心.

为提高样本描述能力，通过贝叶斯信息准则(BIC)来选择聚类簇数. 对于模型M

(7)

式中：L为X上的对数似然函数；Φ为参数集；nΦ为参数数目；γp复杂度的惩罚项.

若单一信号段的BIC值大于包含正常及故障2种信号段的BIC值时，最优聚类簇数Cbest为1，其余为2.

已知信号MFPH特征后，基于FCM与BIC的双门限自适应故障预警流程如图1.

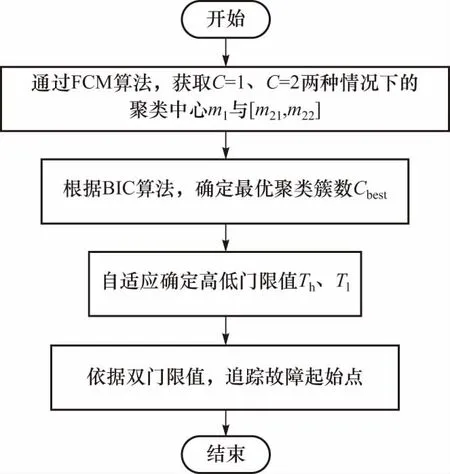
图1 故障预警方法流程Fig.1 Flow of failure warning method

2 VMD的原理与改进

2.1 VMD原理

VMD是一种利用约束优化来解决信号分解问题的信号处理方法，VMD将信号分解为一组模态分量，在分解过程中每个分量的中心频率和带宽不断迭代至最优值，最后将信号进行自适应分解. 优化模型如下

(8)

式中：K为模态分量的个数；{uk}为分解的模态分量；{ωk}为{uk} 的频率中心；f为输入信号.

对uk、ωk和λ进行交替迭代寻优，迭代公式如下

(9)

(10)

(11)

式中γ直到满足给定精度ε，迭代停止，得到最终的模态分量及相应的频率中心.

2.2 VMD改进

研究表明，VMD算法中分量个数K和惩罚参数α选取不当会产生模态混叠，且实际信号中噪声严重，K和α的值无法准确设定[15]. 因此本文提出一种能量差网格搜索法，以原信号能量和分解分量能量和之差最小为目标，搜索最优K和α，参数搜索区间基于大量测试函数和实际信号进行实验后设定，具体流程如下：

① 在[K,α]的网格中，设定K的搜索区间为[2,10]，步长为1，设定α的搜索区间为[200,10 200]，步长为250；

② 获取网格点对应的[K,α]值，对输入信号s(t)进行VMD分解；

③ 计算输入信号s(t)的能量值与K个分量能量和的差值，更新全局最小能量差，并按步长遍历整张网格.

在信号分解中，VMD在信号截断和外界因素的影响下会出现端点效应，严重影响了分解精度. 针对端点问题，通常采用边界延拓来抑制. 支持向量回归机(support vactor regression，SVR)以统计为基础，通过核函数解决非线性拟合问题，可依据小样本得到全局最优值，衡量和真实值的预测误差[16]. 支持向量回归机SVR模型如式(12)，对于给定的样本D={(xi,yi)}，可使f(x)与y尽可能接近

(12)

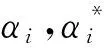
SVR抑制端点效应的具体步骤如下：

① 取长度为N的样本信号，用SVR对其进行左右延拓，延拓个数分别为NL和NR；

② 对延拓后长度为N+NL+NR的信号进行VMD分解；

③ 将分解后的各分量在左右两边分别舍弃NL、NR个点，保留中间N个数据为最终样本分量.

2.3 改进效果分析

利用仿真信号来验证改进VMD的有效性. 信号y(t)包含频率为50 Hz和80 Hz的2个分量，采样频率1 kHz，采样时间1 s.

(13)

通过能量差网格搜索法得到VMD的最优[K,α]的值为[2，450]. 图2为经SVR延拓的信号时域对比图，SVR通过预测与真实信号的全局最小误差，有效地对原始信号进行延拓.

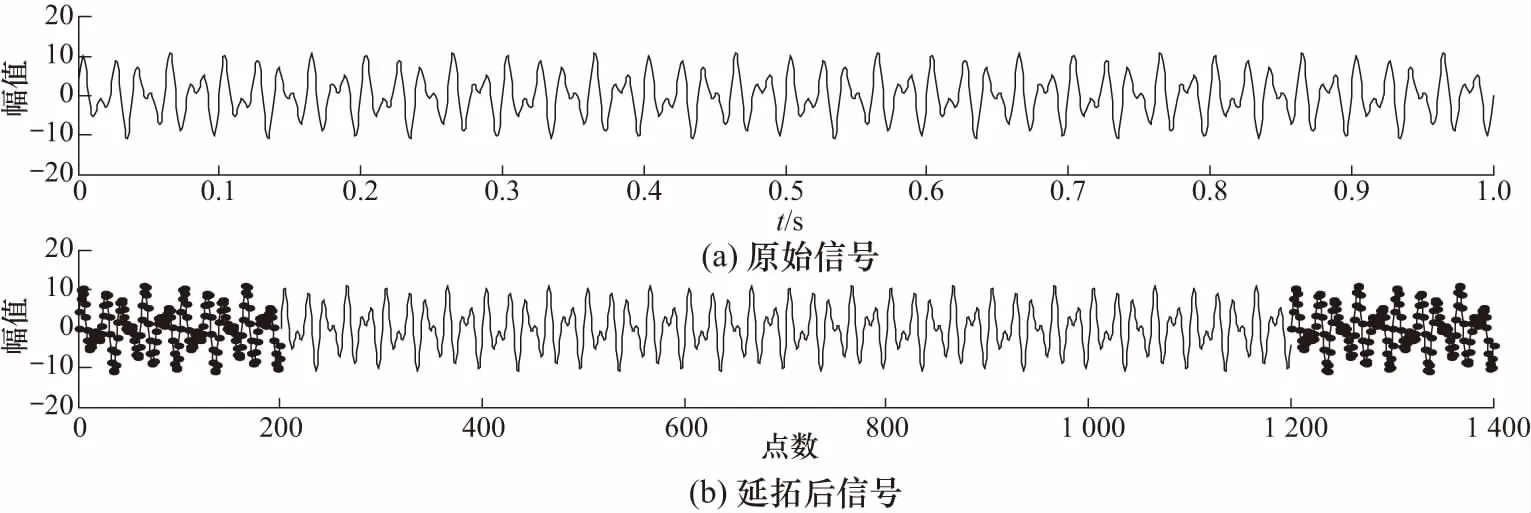
图2 原始信号和延拓后信号时域波形Fig.2 Time domain waveform of original signal and extended signal

图3为SVR延拓前后VMD分解的时频对比图，图中阴影为原始VMD分解，虽然能将频率接近的分量进行有效分离，但分量均产生“端点飞翼”现象，并且由频谱图可见信号模态混叠严重. 改进VMD分解为实线部分，能有效区分各频段的信号分量，验证了该方法在抑制端点效应及模态混叠问题上的有效性.

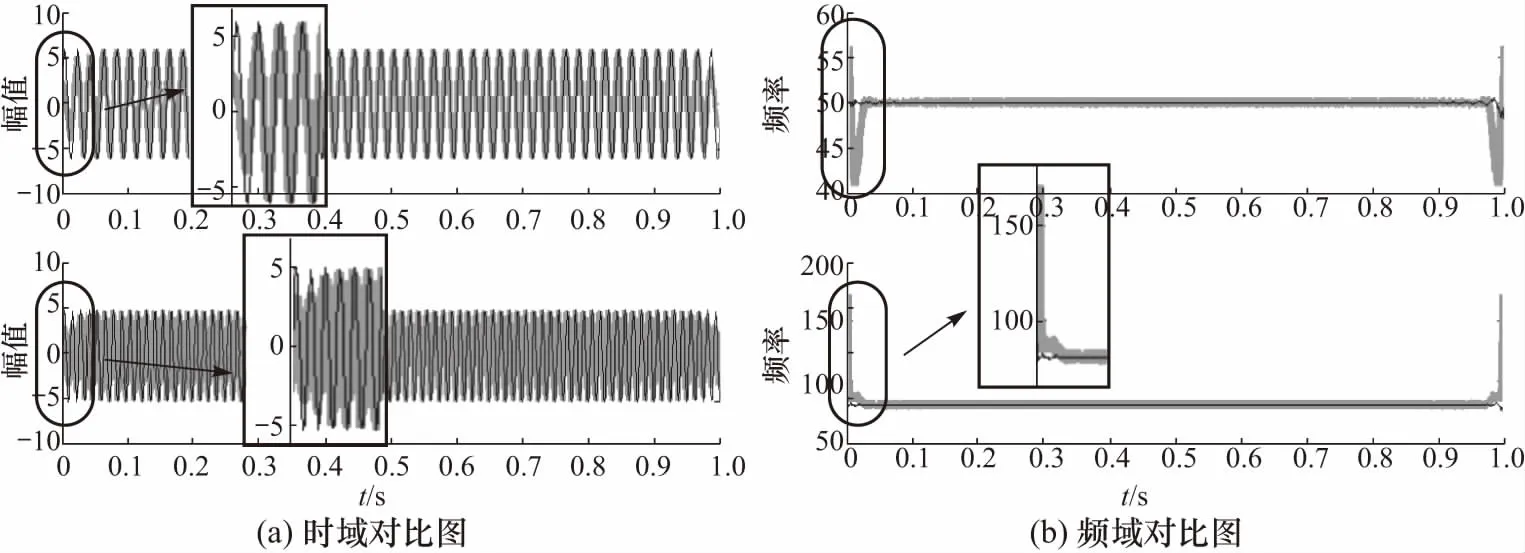
图3 延拓前后各分量时频对比图Fig.3 Time frequency comparison of components before and after extension

3 多尺度加权排列熵原理

3.1 加权排列熵

排列熵以相空间中子序列的排序方式来计算概率，时间序列越规则PE越小. 然而PE忽略了序列数值的变化，对特征提取精度产生了影响. 加权排列熵对其进行了改善，步骤如下：

① 对时间序列x(i)，以时间延迟τ，取m个样本进行空间重构得到X；

② 对重构分量X(i)按升序重新排列：

x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤

…≤x(i+(jm-1)τ)

(14)

③ 排序后，每行重构分量得到一组新的符号序列C′={c′(1),c′(2),…,c′(l)}，其中l≤m!;

④ 计算每种排序的概率P，得出时间序列x(i)的加权排列熵归一化模型

Hp(m)=Hp(m)/ln(m!)

(15)

3.2 尺度加权排列熵

MWPE克服了WPE单一尺度的不足，充分表征了多个尺度的时间序列复杂性. 弥补了提取轴承早期故障特征细节上的不足，更能发挥VMD在轴承预警上的优势，过程如下：

① 对时间序列x(i)进行粗粒化处理

(16)

式中s为尺度因子.

② 计算不同s下，粗粒化序列z(s)的MWPE值

(17)

3.3 基于MFPH和改进VMD故障预警

本文针对传统轴承故障预警采用故障段数据分析，实时性较差的问题. 提取轴承信号MFPH参数，利用双门限法搜索故障起始点，采集起始点后的振动数据进行早期故障预警. 结合MWPE在检测动力学突变行为方面的优势，增强改进VMD提取信号特征的准确性，基于支持向量机进行预警分类验证. 提出基于MFPH故障起始点检测的改进VMD-MWPE故障预警方法，步骤如下：

① 采集轴承信号MFPH特征，依据双门限值确定故障起始点；

② 从起始点后采集故障样本，进行改进VMD分解，获取模态分量，并对分量进行粗粒化处理，得到新的序列zi；

③ 计算zi的MWPE值，并构建特征向量T=[H1H2…HK]，其中K为模态分量个数；

④ 将得到的特征集输入PSO优化的SVM进行训练，获取SVM预测模型；

⑤ 将故障段数据按步骤②～⑤提取特征向量，通过SVM进行早期故障预警.

4 实验分析

为验证本文预警方法的有效性，以图4上海频询机械故障综合模拟实验台所采集的数据为样本. 结合USB-1608GX-2AO的DAQ设备、加速度计及LabView进行采样. 由于实验条件限制，无法准确从某一刻制造故障，因此将同等条件采集的正常信号与故障信号拼接作为研究对象，故障段包括滚动体故障、内圈故障、外圈故障.

图4 轴承故障模拟实验台Fig.4 Bearing fault simulation test bed

4.1 MFPH故障点检测

在采样频率为8 kHz条件下，取4 000个正常振动信号数据分别与内圈、外圈和滚动体故障数据各4 000个进行拼接，理论上在t=0.5 s时会检测到故障起始点. 以内圈故障为例，如图5所示，正常段信号MFPH门限值在[0,2]区间，内圈故障在[-2,-3]处，有明显区分度.

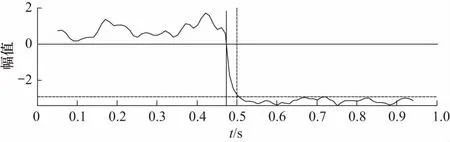
图5 内圈故障起始点检测Fig.5 Starting point detection of inner race fault

双门限MFPH提取短时能量和短时过零率等特征参数，适用于高信噪比环境下的端点检测[17]. 因轴承工作环境复杂，为了进一步验证MFPH检测效果，将待测信号加入5 dB的低信噪比白噪声. 如图6所示，虽然MFPH特征受噪声影响，但故障起始点时刻仍在t=(0.5±0.02) s范围内，证明该方法可在噪声环境下作为起始点检测依据.

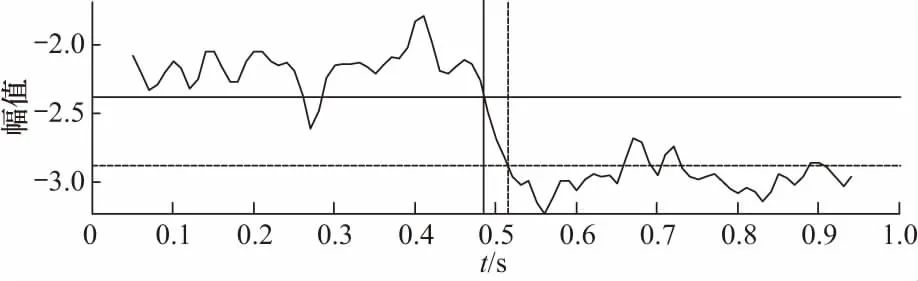
图6 白噪声环境下内圈故障起始点检测Fig.6 Starting point detection of inner race fault in white noise environment

为验证方法普遍性，重新采集样本，分别对3种故障拼接段各100组重复上述实验，统计漏检、错检情况及正确率如表1所示. 标准环境准确率为98.32%，白噪声环境下准确率仍达96.65%，表明该方法应用于轴承故障起始点检测的有效性.

表1 故障预警实验结果Tab.1 Experiment results of failure warning

4.2 VMD参数选择

本文利用能量差网格搜索法来确定VMD的参数[K,α]，不同参数会对分解产生重要影响.K值过小会导致特征缺失，过大则产生模态混叠，影响分量带宽的大小. 以滚动体故障为例，取一组点数为1 200的数据，用能量差网格搜索法进行参数寻优得到最佳参数[K,α]=[4,4 200]，对应的最小能量差为3.313，能量差网格图如图7所示.

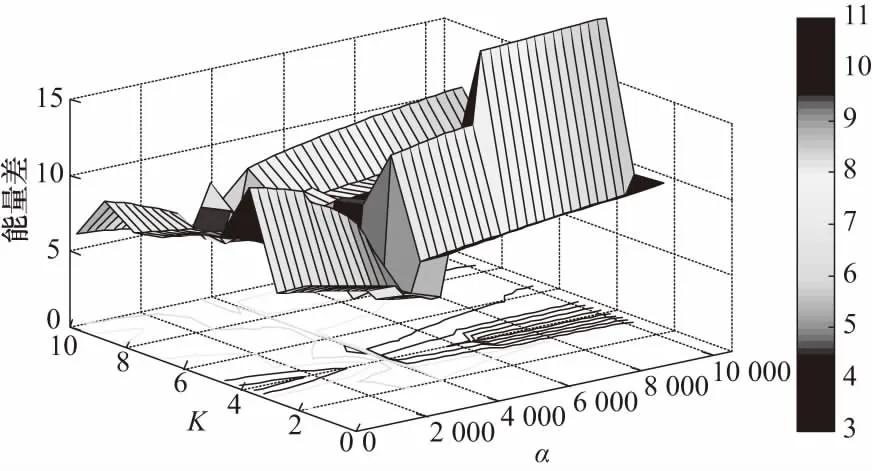
图7 0滚动体故障VMD分解最小能量差值图Fig.7 VMD decomposition minimum energy difference diagram of rolling element fault

4.3 改进VMD和MWPE的特征提取

将VMD参数设定为寻优后参数，以滚动体故障为例，采用上文选定参数[K,α]= [4,4 200]，对比改进前后VMD分解效果，如图8,图9所示，VMD分解中，前2个分量频带中心不明显，频带分别集中在164～1 436，2 602～2 848 Hz之间，分量3、4有严重混叠部分，而采用改进VMD分解的分量频谱清晰，在提取特征中有明显的优势.

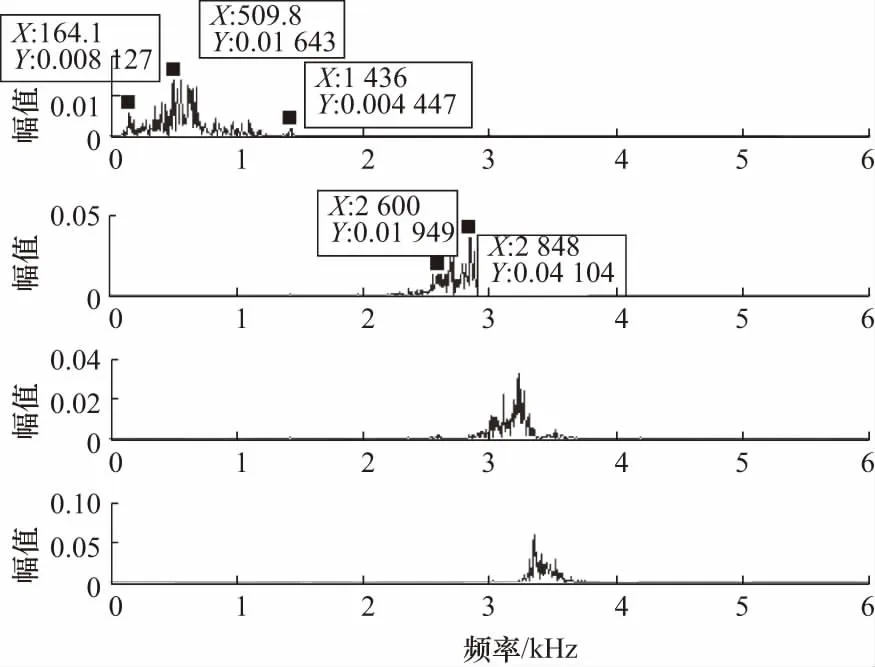
图8 VMD分解频谱图Fig.8 VMD decomposition spectrum

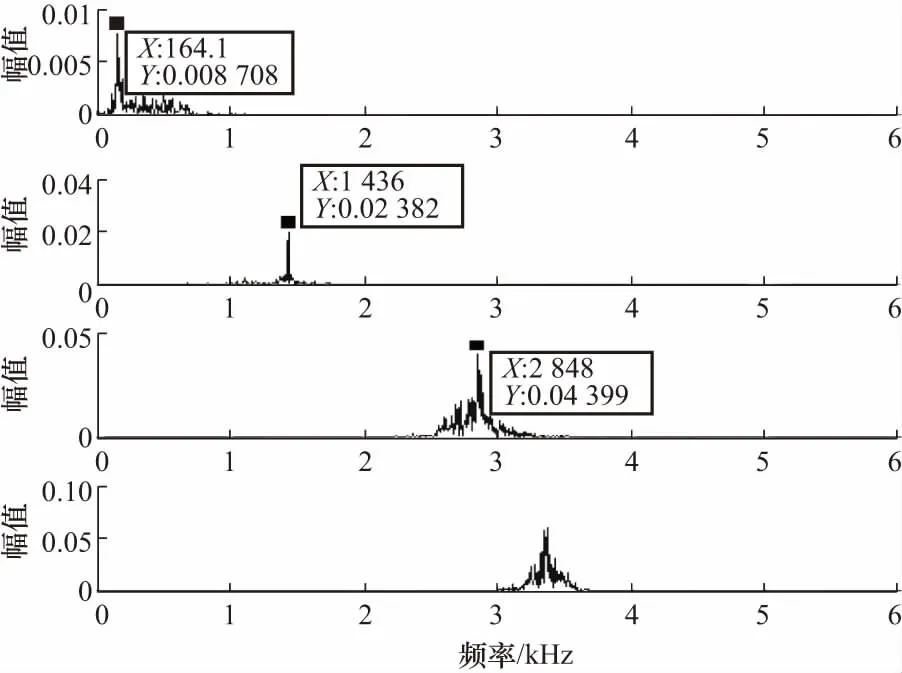
图9 改进VMD分解频谱图Fig.9 Improved VMD decomposition spectrum

为了进一步验证本文改进VMD的优势，采用SVR对EMD进行延拓，与本文方法进行对比. 图10为延拓后EMD的分解结果，得到了9个IMF分量. 对比发现EMD早期故障特征混叠严重，且虚假分量多，分解效果较差. 综上，证明了本文改进VMD方法在提取故障特征频率方面的优越性.

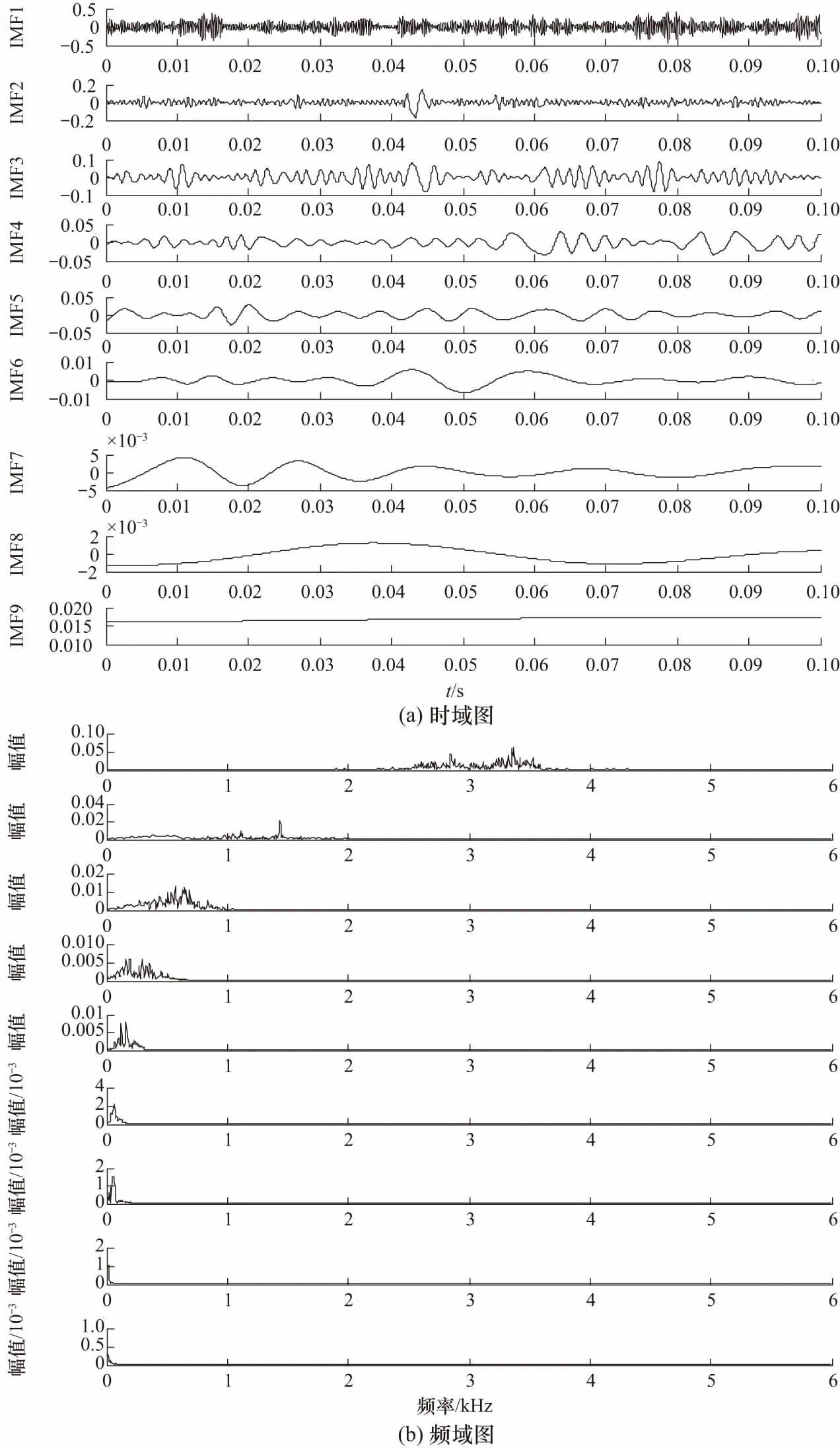
图10 SVR延拓后EMD分解时频图Fig.10 EMD decomposition time-frequency diagram after SVR extension

为进一步发挥VMD优势，更准确地提取早期故障特征以达到良好的预警效果. 对正常、内圈、外圈及滚动体故障4种状态各取10组数据，每组1 000个点，WPE和MWPE的重构分量维度m=5，时间延迟τ=2，MWPE的尺度因子s=10. 基于本文改进VMD-MWPE特征提取方法，构建特征向量. 如表2所示，MWPE特征相比WPE，方差更小，证明了MWPE的稳定性更强、类间差异性更优，进一步验证了MWPE能更精准地提取故障特征.

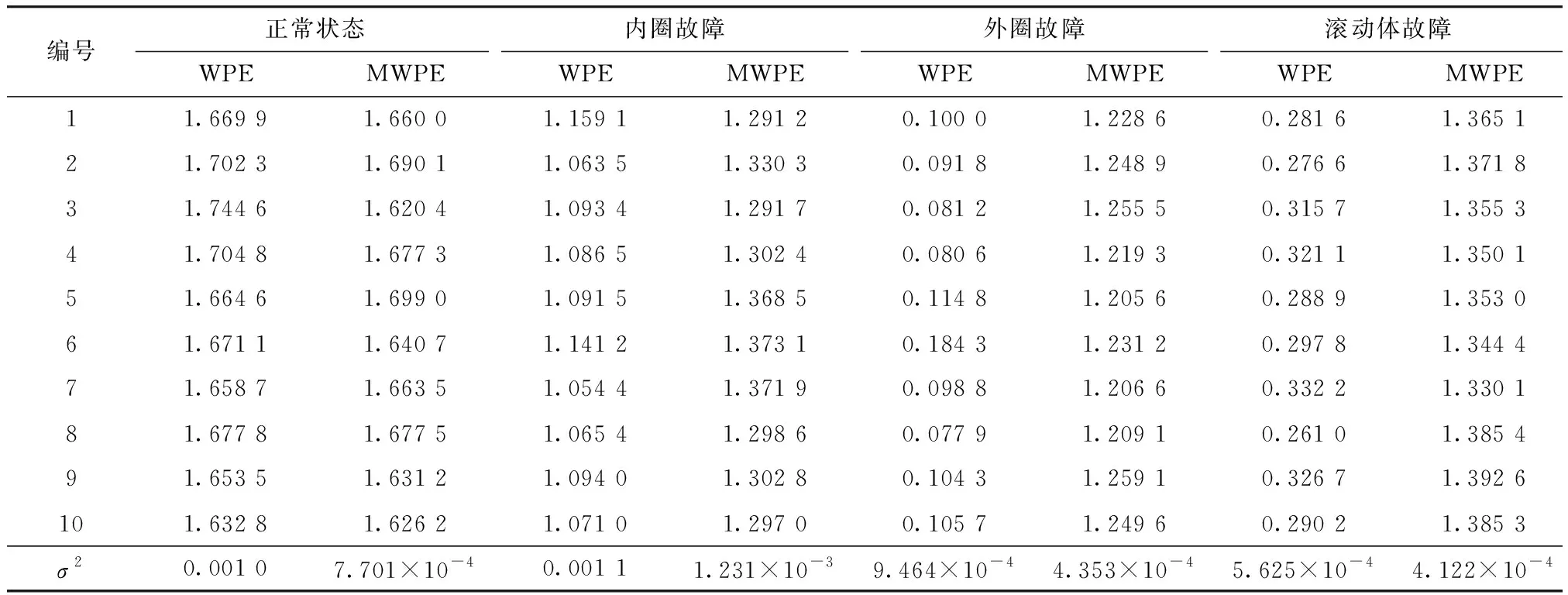
表2 4种状态下振动信号的WPE和MWPETab.2 WPE and MWPE of vibration signal in four states

4.4 故障预警效果分析

基于MFPH的双门限法确定故障起始点后，采集早期故障数据进行VMD-MWPE特征提取进行故障预警，提高了预警模型的实时性. 为进一步验证本文方法，将采集的100组数据，分别通过改进前后的VMD进行分解，并分别计算WPE和MWPE为特征向量，将特征向量输入到PSO优化的SVM，60组数据进行训练，40组进行测试，结果如表3所示.

表3 故障识别率对比表Tab.3 Comparison table of fault identification rate

表3验证了MWPE以时间序列随机性和微弱信号敏感性的优势，使VMD得以充分发挥，通过SVM测试后，对样本识别率平均高达98.75%，准确率远高于其他3种方法，验证了本文预警方法的可行性.

5 结 论

本文将语音端点检测思想加以迁移，提高了故障预警的实时性，研究了改进VMD-MWPE的特征提取方法，通过仿真信号和实际数据分析可知，本文方法在故障特征捕捉中具有一定优势.

① 将MFPH特征作为故障点判别依据，利用BIC算法确定是否包含起始点，通过FCM对信号段门限值进行自适应估计，最后依据双门限进行故障起始点检测.

② 改进VMD自适应确定分解层数K和惩罚因子α，解决了参数难以确定的问题；结合SVR良好的泛化能力对信号进行延拓，解决了VMD的端点效应问题，并有效地抑制了模态混叠现象.

③ 振动信号表现了动力学突变行为，基于MWPE对动力学突变行为检测的优势，提高故障特征的准确性.

④ 基于起始点检测的实时优势，结合改进VMD-MWPE对轴承故障特征的准确提取，保证了故障预警的可靠性.