电动静液作动器的自适应变阻尼滑模控制
付永领, 李宇鹏, 王明康, 林自旺, 朱德明
(1. 北京航空航天大学 机械工程及自动化学院, 北京 100191; 2. 北京精密机电控制设备研究所, 北京 100076)
在多电/全电飞机的趋势下,新型的电传作动器包括电静液作动器(electro-hydrostatic actuator,EHA)和机电作动器(electromechanical actuator,EMA)得到了快速发展[1-2]. EHA相比于EMA,它具有液压的自润滑作用且没有机械结构的卡死问题,因而在现阶段被广泛应用. 然而EHA也有着自身需要解决的问题,如参数随着外部环境的时变性问题、液压缸本身的摩擦和泄漏带来的死区和参数不确定性等[3].
因此,许多学者提出了多种方案来尝试解决上述问题. 如多环级联的模糊自适应PID方法,但该方法中模糊规则的设计过度依赖经验和专家系统[4-6]. 此外,反馈线性化控制、模型参考自适应控制、H∞控制、反步法控制等方法也被应用到EHA的控制中以期提高系统的鲁棒性[7-9]. 再者,一些人工智能的控制方法也在EHA领域进行了初步尝试,如基于灰度预测的PID控制、基于神经网络的反步法控制等等,不过此类方法或全局寻优要求较高的硬件算力,或需要系统状态全部可测,给EHA的驱动控制均带来巨大的压力[10-11]. 然而,基于自适应鲁棒的方法在伺服阀控上被证明是一种行之有效的控制方法,但是其由于偏微分的存在使得控制量非常复杂,因此在EHA上没有得到广泛的研究[12-13].
滑模控制作为一种鲁棒控制策略,具有对系统外部扰动、内部参数摄动均不敏感的优点,且逻辑简单,有着严格的证明过程和理论支撑[14-16]. 但它不足之处在于:①需要较大的控制增益和非线性鲁棒项来压制系统的不确定性,这种不连续“过度”补偿容易导致系统稳态时的抖振;②把系统全部的不确定性完全依靠鲁棒项处理,这就使得鲁棒项的任务过大. 针对这两个问题,YANG[17]提出一种新型的自适应趋近律和滑模观测器分别用来抑制抖动和观测外部扰动,然而这种新型趋近律方法过于复杂,实现困难. 张振等[18]提出一种模糊滑模控制来改善抖振,这种模糊规则也过于依赖经验设计. 付永领等[19]设计的变阻尼滑模(damp variable sliding mode control, DV-SMC)能够改善EHA的阶跃响应性能,但是由于变阻尼方法去掉了前馈补偿项,势必造成系统的稳态响应变慢,且该方法没有单独考虑参数不确定性.
针对上述问题,在变阻尼滑模控制的基础上,作者结合自适应律的优点设计了一种新型的自适应变阻尼滑模控制(adaptive damp variable sliding mode control, ADV-SMC)策略. 该方法有如下优点:
① 通过自适应律估计系统的未知参数,实现了参数摄动和外部扰动的分别补偿,从而减小了鲁棒项任务量. 同时重新定义了系统的符号函数来减小稳态抖振.
② 自适应方法的引入补偿了由于变阻尼方法中前馈相缺失带来的动态跟踪性能下降问题,进一步提高了EHA的位置跟踪精度.
1 EHA系统模型
EHA工作原理如图1所示,驱动控制器接受上位机指令,驱动伺服电机,带动双向泵工作,通过液压回路将油液注入油缸,实现作动缸的伸缩,最终将作动杆推动到指定位置.
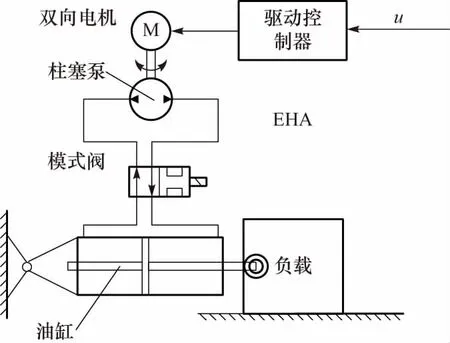
图1 EHA原理图Fig.1 Schematic diagram of an EHA
1.1 直流无刷电机(BLDCM)模型
EHA的伺服电机使用直流无刷电机,绕组采用星形连接,且建模过程中有以下假设:
① 直流无刷电机的绕组参数完全相同;
② 定转子之间的气隙磁场为规则梯形波.
该电机绕组的模型可以写为
(1)
式中:下标U、V和W分别代表电机三相;L*为相电感;i*为相电流;R*为相电阻;e*为相反电动势;UN为三相连接中点电压.
通常直流无刷电机为两两导通方式,因此可以将式(1)改写为
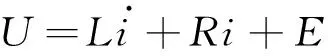
(2)
式中:U、L、i、R和E分别为等效电压、电感、电流、电阻和电动势.
假设直流无刷电机的扭矩系数Kt,则其转动的动态方程为
(3)
式中:Ke为反电动势系数;Te为电磁转矩;Jm为转动惯量;TL为等效外负载;Bm为黏性摩擦因数.
1.2 泵控液压缸模型
根据泵的工作原理,其进口流量qVi和出口流量qVo为
(4)
式中:Dp为排量;Li为内泄漏系数;Lo为外泄漏系数;pi、po和pa分别为入口压力、出口压力和油箱压力;Vin和Vout为入口和出口的等效容腔体积;βe为油液的弹性模量.
油缸的动态方程为
(5)
式中:下标l和r分别表示油缸的左右两腔;A为活塞有效面积;x为活塞位移;Lc为油缸的内泄系数.
忽略阀块中的压降损失,由流量连续性定理,有qVl=qVi,qVr=qVo. 联立式(4)和(5)则泵和油缸模型为
(6)
式中:V0为容腔有效体积;La为泵和油缸总的泄漏系数,并且与压差Δp成正比;qVa为其他流量损失;M为油缸和负载总的等效质量;Bc为油缸的黏性摩擦因数;Ks为弹性负载系数;Ff和FL分别为静摩擦力和外负载.
(7)
式中:Ja为泵和电机总的转动惯量;qVun为不可预计的流量损失.
可以看出整个EHA模型是一个以母线电压U为输入,活塞杆位移x1为输出的,存在非线性和非匹配扰动的高阶系统.
2 控制器设计
2.1 坐标转换
分析系统状态空间方程(7),其前2个动态方程表示液压缸的动态,第3个方程表示系统压力的动态,而最后2个方程表征的分别为电机转速和电流的动态. 因此,当将x4视作由式(7)的前3个方程所构成的子系统输入u时,系统模型(7)被拆分成机械液压子系统(简称机液环节)和电机子系统. 这2个子系统的输入分别为电机转速x4和直流母线电压U,输出分别为液压缸的位移和电机转速.
对于机液环节而言,系统存在着非匹配扰动,而滑模方法对非匹配型扰动并不具备鲁棒性,因此需要对机液环节进行坐标转换. 重新定义机液环节的状态变量为
(8)
三阶的机液环节的系统状态方程表示为
(9)
根据重新定义的状态变量,可得:
(10)
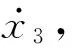
Ksz1-Bcz2-d(Ff+FL)/dt
(11)
(12)
式中:
g3=MV0(AβeDp)-1,A3=LcM(ADp)-1,
A1=KsLc(ADp)-1+KsV0(AβeDp)-1,
Lc(Ff+FL)(ADp)-1.
2.2 自适应变阻尼滑模控制器(ADV-SMC)设计
重新定义系统的参数矢量:
θT=[θ1θ2θ3θ4]T=[A1A2A3g3]T
(13)
那么式(12)可以写为
(14)
假设系统的跟踪目标为xd,那么定义误差及其导数为
(15)
设计变阻尼滑模面为
(16)
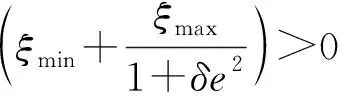
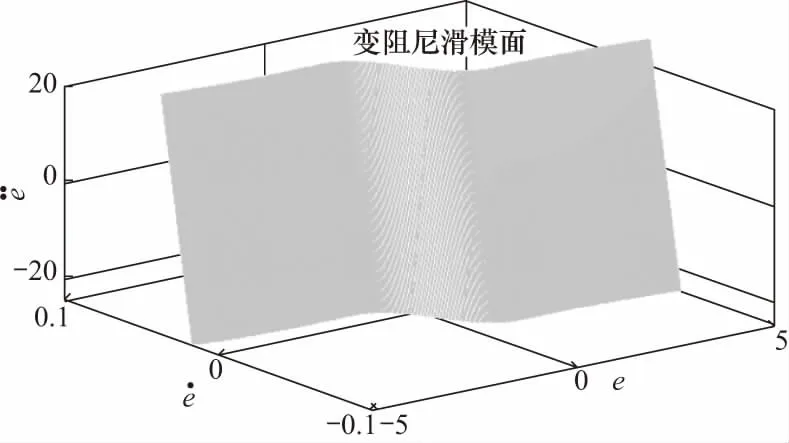
图2 变阻尼滑模面Fig.2 Diagram of the DV-sliding surface
那么,采用常数趋近律设计滑模的趋近过程,即:
(17)
由式(17)可以计算出,系统状态到达滑模面的时间tr为
tr=|σ1(0)|/η
(18)
控制输入u1和自适应律可以设计为
(19)
(20)
设计Lyapunov函数为
(21)
此时系统渐进稳定.
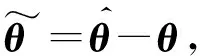
证明对式(21)求其关于时间的导数为
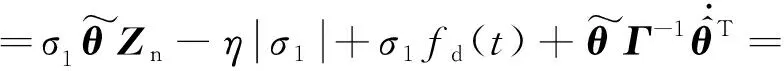
[-η+fd(t)]|σ1|
(22)
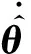
(23)
值得一提的是,为了防止滑模趋于稳态时的抖振现象,重新定义符号函数sgn(*)为
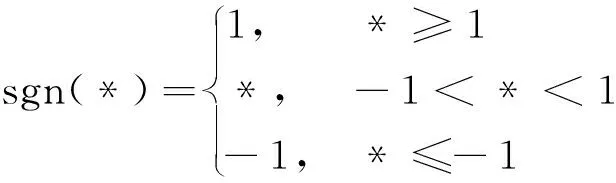
(24)
2.3 电机环节控制器设计
如前所述,对于电机环节的两个动态,可以视为一个二阶系统. 因此可以采用工业中常用的转速-电流双环PID控制器[20]:
(25)
式中:uid和uVd分别表示电机电流和电机母线电压的目标值;k*p,k*i,k*d(*=i,V)分别表示所在控制环路的比例系数、积分系数和微分系数;es,ei分别表示转速偏差和电流偏差.
根据EHA模型式(7)、新型变阻尼滑模控制律式(23)和双环PID控制律式(25),其原理框图如图3所示,即最外环为DV-SMC,内环为双环PID.
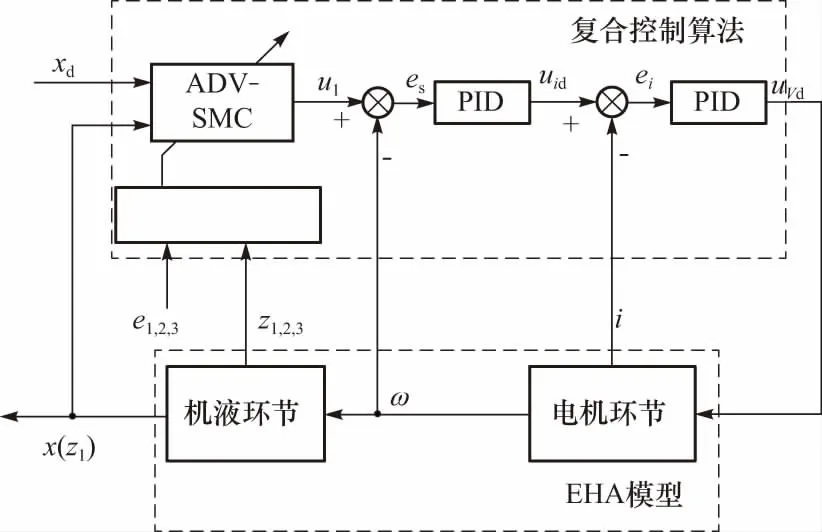
图3 级联控制算法原理框图Fig.3 Schematic diagram of the proposed cascade controller
需要说明的是,从图3中可以看出系统是一个电机和机液串联的系统. 根据主导极点的思想,当前者的动态远快于后者时,可以将前者视作比例环节[14]. 考虑实际情况下,只要保证电机的动态远高于油缸,那么系统的稳定性便可以由式(22)得出.
3 仿真分析
表1中列出了EHA仿真所用相关参数.
仿真中给定3组xd为:
① 0.005 m阶跃指令;

表1 仿真参数Tab. 1 Simulative parameters of the EHA
② 0.05 m阶跃指令;
③xd=0.005sin(2πt)[1-exp(-t3)].
这3组输入分别代表的是小阶跃输入、大阶跃输入、中高频正弦信号,几乎包括了EHA的全部工况,以便能够对控制器的性能进行充分测试.
每一组输入分别有4个控制器用于比较:
① 工业领域中最常用的PID控制器,控制器参数为:比例系数kp=65 000,积分系数ki=48 500,微分系数kd=0;
② 传统SMC控制器,控制器参数为:c1=70.7,c2=2 500,ηSMC=210.7;
③ 文献[19]中所使用的变阻尼滑模控制器(DV-SMC),敏感因子δ=1,ωn=50,ξmax=1,ξmin=0.1,ηDV-SMC=210.7;
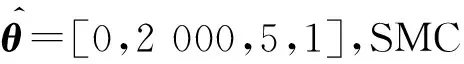
需要说明的是,在②和③中所采用的控制器表达形式与文献[19]相同,在此不再赘述.
3组输入试验的仿真结果如图4,图5所示.
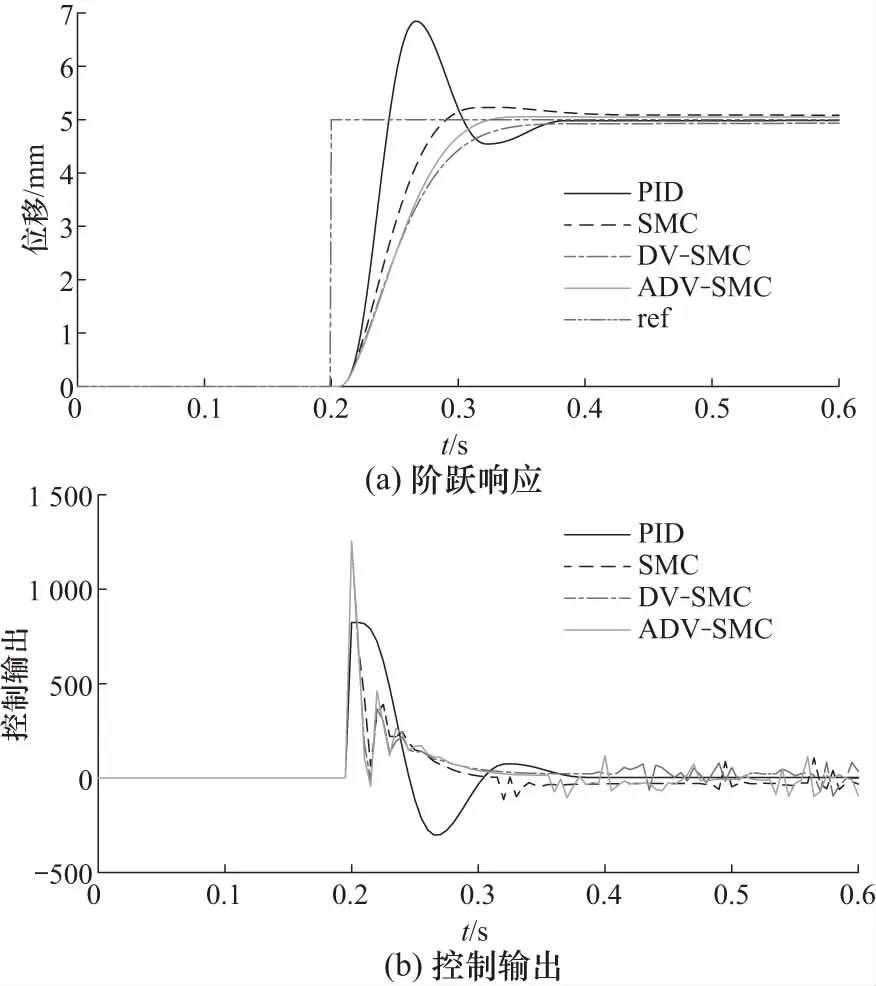
图4 5 mm阶跃仿真结果Fig.4 Simulative results of 5 mm step
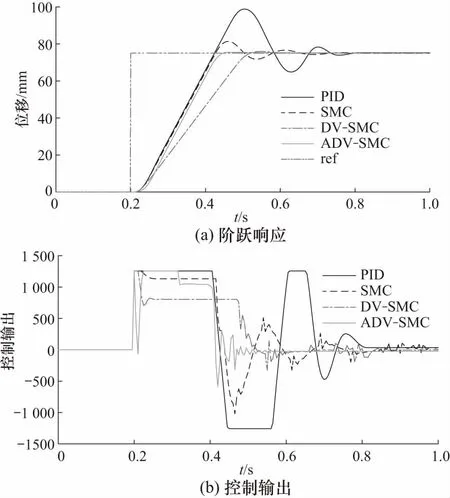
图5 75 mm阶跃仿真结果Fig.5 Simulative results of 75 mm step
分析图4,PID和传统SMC方法均产生了超调分别为1.8 mm和0.45 mm,而DV-SMC和ADV-SMC方法均没有超调,这体现出变阻尼方法对超调效果的抑制作用. 对比后两者则可以看出,由于参数自适应律的作用,新的ADV-SMC方法在精度和快速性上均优于未改进的DV-SMC策略. 图5所示为75 mm大阶跃仿真结果. 通过对比可以看出,随着阶跃幅值的增大,PID和SMC的超调现象更加明显,这也体现出变阻尼对超调的抑制效果. 同样,增加自适应后的DV-SMC策略在快速性上也更加具有优势. 但是值得一提的是,由式(18)可以看出参数的自适应效果是基于积分作用的,这就要求调整时间足够长. 从阶跃仿真结果中虽然能够一定程
度上显示出自适应律的优势,但由于调整时间短,参数适应的效果不能够完全显现. 因此,在正弦仿真中将加长仿真时间.
图6所示为正弦指令的仿真结果,引入[1-exp(-t3)]的目的是使指令更加平滑. 图6~图8分别为位置跟踪误差、控制量和ADV-SMC方法的参数估计结果. 从图6中发现, 1 Hz正弦指令下,PID方法的稳态最大跟踪误差约为7.5×10-4m,SMC方法的稳态最大误差约为2×10-4m,DV-SMC则为2.4×10-4m. 可以看出SMC方法要优于略DV-SMC,因为从控制量输出的表达式看出,变阻尼方法为抑制超调将xd的一、二阶导数均视为0,这相当于在SMC基础上去掉了前馈补偿项,因此就正弦跟踪性能而言SMC方法略有优势.
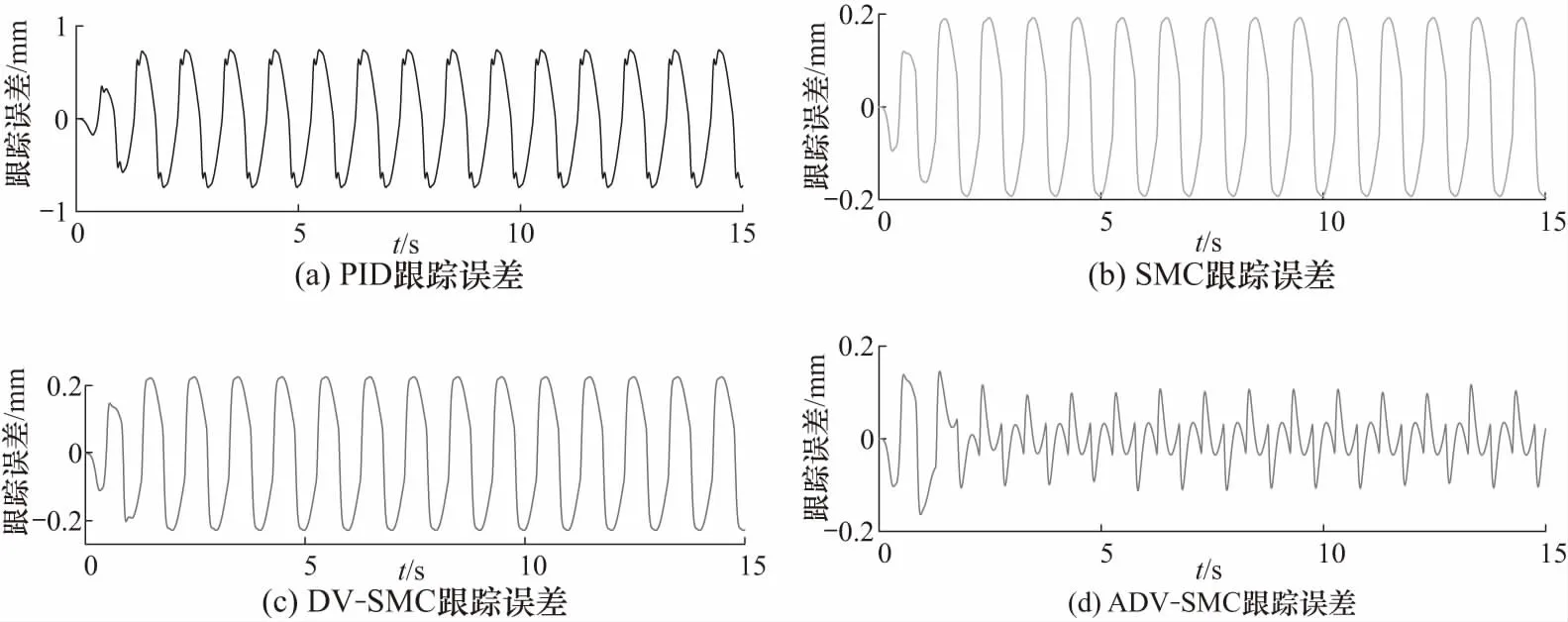
图6 跟踪误差Fig.6 Tracking error
ADV-SMC的稳态最大跟踪误差为约1.1×10-4m. 通过图6可以发现在起始阶段,其跟踪误差和DV-SMC方法相似,这是因为起始阶段由于时间短,自适应律对参数的调整效果有限,导致ADV-SMC和DV-SMC方法的输出差异较小. 随着时间的拉长,观察图8可以看出参数θ1和θ4分别趋向于最大和最小值,这体现出了Proj(*)函数的非线性映射作用.θ2和θ3则分别趋向于稳定范围内,此时的跟踪误差明显得到抑制,这证明了参数自适应对系统跟踪性能的促进作用. 从图7的控制量输出也能够得出类似的结论:PID的控制输出在活塞杆速度换向点是连续的,而由于死区的影响,连续的控制量必然会造成大的跟踪误差. 而后三者在该处均有一个输出“尖峰”,这个尖峰源于鲁棒项,它能够抑制摩擦的作用使得EHA能够更快地跨过死区. 同时,在自适应律的作用下ADV-SMC在死区的控制作用更加明显,进而获得更好的控制效果.
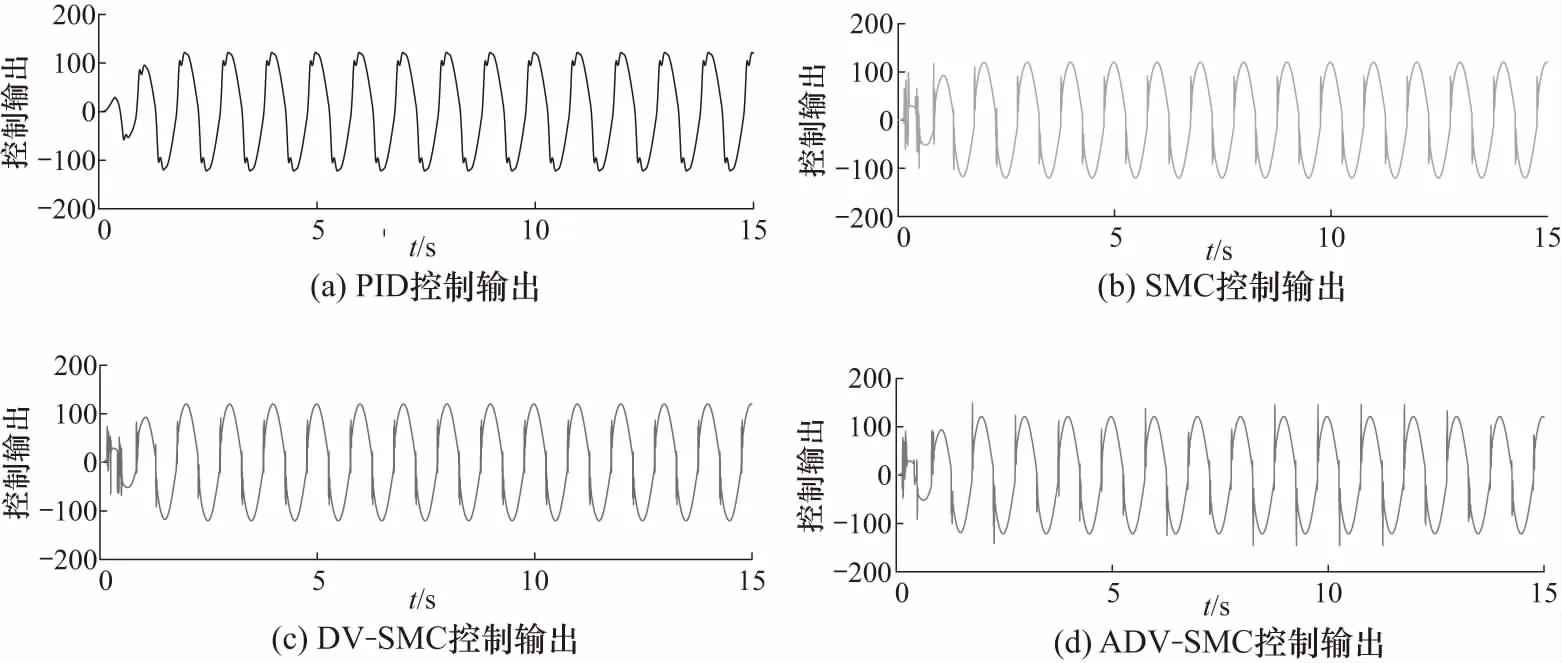
图7 控制输出Fig.7 Control output
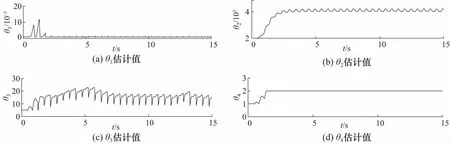
图8 参数估计Fig.8 Parametric estimation
4 结 论
① 对于EHA中存在的慢变参数的不确定性,自适应控制是一种有效的方法,它能够在线估计系统的未知参数;
② 相比于变阻尼滑模,引入自适应策略能够进一步提高EHA位置跟踪的快速性和精度;
③ 本文所设计的控制策略能够有效改善变阻尼滑模控制过程中由于忽略前馈项带来的误差增大现象. 且随着参数估计的逐渐稳定,能够进一步减小系统的位置跟踪误差.

