基于峰度系数方差的加权自适应引导滤波
方红萍, 曾若云, 吴家鑫, 伍世虔
(1.武汉科技大学 信息科学与工程学院,湖北,武汉 430081;2.武汉科技大学 机器人与智能系统研究院,湖北,武汉 430081)
图像滤波是图像处理中重要的预处理环节. 目前图像滤波方法大致可分为两类. 第一类是变换域滤波算法,如傅里叶变换[1]、离散余弦变换[2-3]、小波变换[4-5]等. 这类算法具有边缘保持能力,但易产生吉布斯效应[6]或梯度反转[7]等问题. 第二类是空间域滤波算法,如均值滤波[8-9]、高斯滤波[10]、双边滤波BF[11-12]和引导滤波GIF[13-18]等. 均值滤波和高斯滤波的核函数与图像域信息无关,所有局部窗口操作相同,能去除噪声但是容易引起边缘模糊. BF和GIF均具有去噪保边能力. BF核函数权重综合考虑空间域和图像域两方面信息,采用双高斯滤波相结合的方法进行滤波,但是存在计算复杂度高、梯度反转等问题. GIF引入引导图Q,假设滤波输出图像和引导图像满足局部窗口线性关系,将滤波问题转换为一个线性参数的优化问题. GIF算法效率达到O(N)水平,能避免梯度反转. 但是仍存在一定的局限性.
首先,GIF对整张图像进行处理时,所有窗口均使用固定正则化参数ε,并没有针对窗口不同结构信息,自适应地调节正则化参数ε,因此在边缘附近容易出现边缘模糊和光晕效应. 梯度引导滤波GGIF[19]在GIF的基础上,引入一种基于局部窗口方差的边缘敏感函数来描述图像结构信息. 采用新的惩罚因子ε/Γω k代替原有的固定ε,实现自适应引导滤波. 虽然该算法具有更优的边缘保持特性,但是图像中噪声的引入,使局部方差感知边缘的能力下降,从而影响最后的滤波效果.
其次,GIF和GGIF两类滤波方法均在最后输出结果时,对输出像素采用求算术平均的方式进行聚合. 当边缘区域的某一像素被多个较平坦区域的窗口所包含时,利用算数平均聚合输出必然会使结果比真实值要小,从而造成边缘模糊.
本文主要从上述两个问题出发,针对有噪图像滤波问题,定义一个对噪声不敏感的边缘感知函数,然后在此基础上提出一个基于边缘权重的加权自适应引导滤波器WAGIF,实现有效去噪的同时,提高边缘保持的能力.
1 基于峰度系数方差的边缘感知
峰度又称峰态系数. 在统计学中,峰度主要用来表征实数随机变量概率分布的峰态. 标准正态分布的峰度为3. 一般以正态分布为标准,描述其他分布的密度形状是否陡峭或平坦. 当峰度大于3,表明形态较陡峭,数据中偏离均值的极端差异值较多;反之,说明形态较平坦,差异值较少.
对于包含高斯白噪声的图像P,假设以像素P(i)为中心的局部窗口ωk中,像素分布服从某一概率分布,μp为窗口ωk的均值,则窗口ωk的峰度计算如下.
(1)
已知噪声图像像素P(i),满足
P(i)=P′(i)+N(i),i∈ωk
(2)
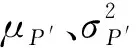
i∈ωk
(3)
噪声为高斯白噪声,服从高斯分布,所以满足
(4)
基于上述计算,分析Kωk(p)如下.
1) 当P′(i)所处局部窗口ωk为近似平坦区域时,P′(i)→μP′,P′(i)所在窗口ωk的四阶矩,二阶矩和方差趋近于0,则
(5)
2) 当P′(i)所处局部窗口ωk为非平坦区域时,分两种情况讨论.
≪
i∈ωk,P(i)∈P
(6)
按照如上推导可知,Kωk(p)满足远小于3.
3,i∈ωk,P(i)∈P
(7)
此时,Kωk(p)满足远大于3.
图1显示了噪声图像不同区域的峰度值,其中1(a)是原始图像,1(b)和1(c)是都添加了方差为0.002的高斯噪声图像. 1(b)中黑框为复杂纹理区域,其峰度值为5.002 3,而1(c)中黑框位于具有噪声的平滑区域,峰度值为2.886 4,接近常数3.

图1 噪声图像中不同区域峰度系数对比Fig.1 Comparison of kurtosis coefficients in different regions of noise images
鉴于上述公式推导分析和二维图像峰度值计算结果,本文针对有噪图像,也将3作为标准峰度,定义相对峰度系数eωk(p)为
eωk(p)=Kωk(p)-3,p∈P
(8)
可得结论:当eωk(p)≫0,说明ωk为边缘或纹理较强区域;当eωk(p)≪0,说明ωk为弱纹理区域;而当eωk(p)→0,ωk窗口为平坦区域.
但是在实验中发现,直接使用eωk(p)对边缘纹理区域的定位存在一定偏差. 比如图2中的一维有噪阶跃信号(噪声方差为0.002,ωk窗口半径r=8),在其有噪声的平坦区域,eωk(p)接近0,此时eωk(p)值和理论分析一致,能有效表征平坦区域,且对噪声敏感度低;在强边缘区域,其eωk(p)远大于0. 但是在边缘定位上结果不令人满意. 比如,真实边缘点e1处并没有出现理想的峰度极大的单峰状态,反而其前后两侧出现两个伪单峰,边缘点e1处的eωk(p)值处于两伪单峰的偏谷底区域. 通过分析不难发现,当局部窗口ωk中心滑动到处于a、b时,ωk分别处于“开始进入边缘”和“准备滑出边缘”状态. 此时,ωk窗口内均开始出现一个突变值,相对于窗口均值,这个突变值的差异很大,峰度作为四阶矩会进一步放大这个差异,从而在a、b处各形成一个峰度系数峰值. 而滑动窗口ωk中心处于真实边缘点e1时,窗口中两类像素数目相当,偏离均值的差异值反而下降,出现峰度系数值变小问题.
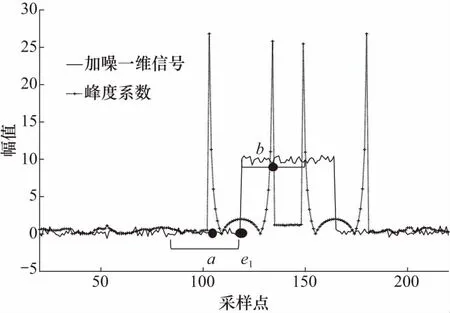
图2 加噪一维信号的峰度系数(r=8,噪声方差为0.002)Fig.2 Kurtosis coefficient of noisy one-dimensional signal (r=8, noise variance is 0.002)
如图3所示,GGIF中基于方差的边缘感知方法,平坦区域的方差会随着噪声的引入而增加. 而本方法,受噪声影响的平坦区域其峰度系数方差几乎为0,对噪声敏感度大大降低;在边缘点e1处呈现单峰状态,其针对噪声图像边缘感知和定位能力更强.
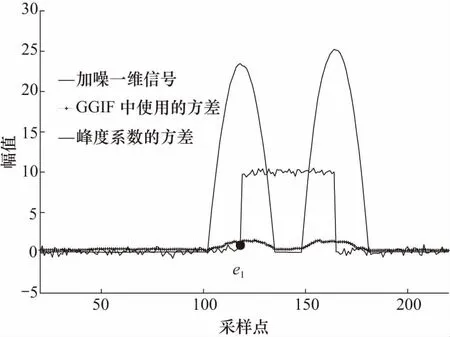
图3 有噪一维信号边缘感知结果对比Fig.3 Comparison edge perception results for one-dimensional noise signals
在此基础上本文设计了一种基于峰度系数方差的边缘感知函数Γωk(p)为
(9)
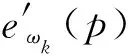

图4 边缘权重图对比Fig.4 Comparison of various edge weight maps
2 基于峰度系数方差的加权自适应引导滤波
2.1 方法的提出
1) 基于图像的边缘权重图信息,设计新的正则化参数自适应引导滤波策略.
新的代价函数定义为
E(ap,bp)=
p∈P
(10)
式(10)的系数ap、bp计算如下.
(11)
bP=μQ-aPμP
(12)
式中:μP为图像P窗口ωk的均值;μQ为引导图像Q窗口ωk的均值;|ω|为窗口ωk像素个数.
2) 在上述基础上,设计新的滤波结果加权聚合策略.
由于滤波窗口中的每个像素点都包含在其周边多个邻域窗口内,GIF直接对这些窗口的滤波结果求平均值,不可避免的造成边缘模糊. 因此本文在求得Γωk之后,对每个窗口的Γωk进行加权聚合如公式(14)所示,当局部窗口位于较平坦区域,权重较小,反之亦然. 所以本文WAGIF方法的最终输出Z(p)计算如下.
(13)
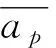
(14)
(15)
2.2 方法的分析
针对上述两个方面的改进,选取引入方差为0.002一维信号作为输入. 其中各滤波方法的窗口半径r和初始正则化参数ε分别为(2,0.2),(4,0.4).
2.2.1正则化参数自适应引导滤波策略结果分析
为分析方便,假设输入图P和引导图I一致,此时系数ap的计算如式(16)所示.
(16)
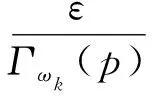
后文为描述方便,将上述仅改进自适应引导策略的滤波器方法取名为AGIF. 从图5(a)和图5(b)的边缘细节放大处可以明显看到AGIF滤波后的边缘更接近原始信号的边缘,在存在噪声的情况下,其保边效果优于GGIF.
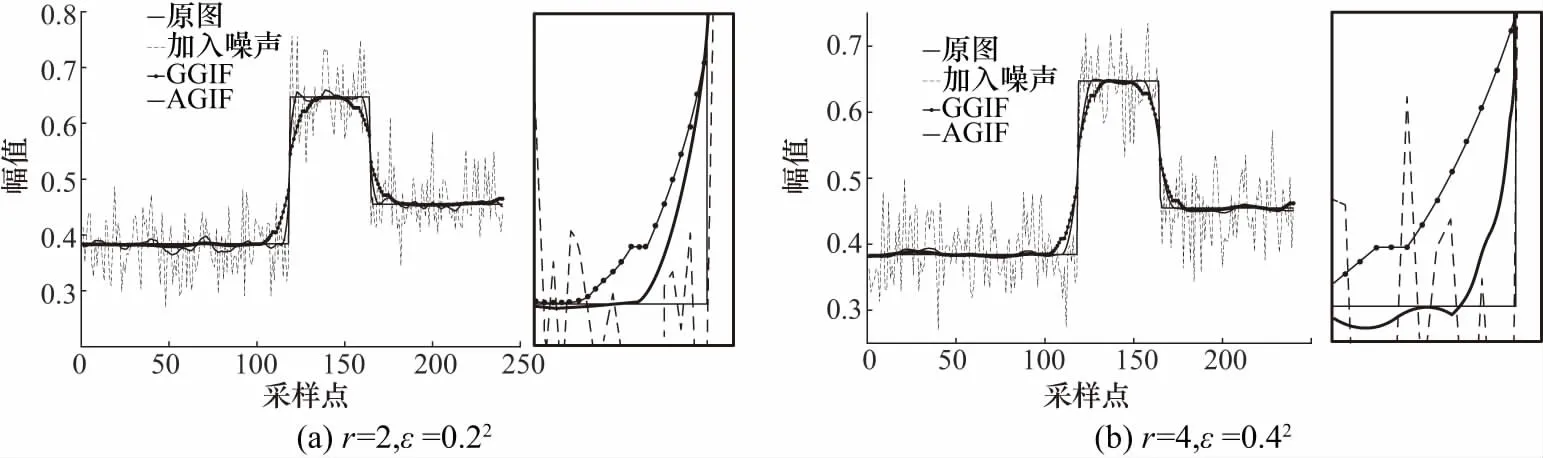
图5 不同r和ε下一维噪声信号的AGIF滤波结果Fig.5 AGIF filtering results for one-dimensional noise signals with different r and ε
2.2.2加权聚合引导滤波策略结果分析
本文的加权函数如式(13)所示,当窗口ωk越接近平坦区域,权重Γωk(p)相应越小,分配给输出像素的权值就越小;反之当窗口ωk越接近边缘区域,Γωk(p)就越大,分配给输出像素的权值就越大.
图6(a)边缘信号细节放大图可看出,加粗实线表示的WAGIF比细实线表示的GIF更“尖锐”,且比虚线代表的AGIF算法更接近真实信号的边缘. WAGIF在AGIF基础上能达到更好保留边缘信息目的. 同样地,加大窗口半径到4后,从图6(b)中看出WAGIF滤波后的边缘信号也更接近原始信号.
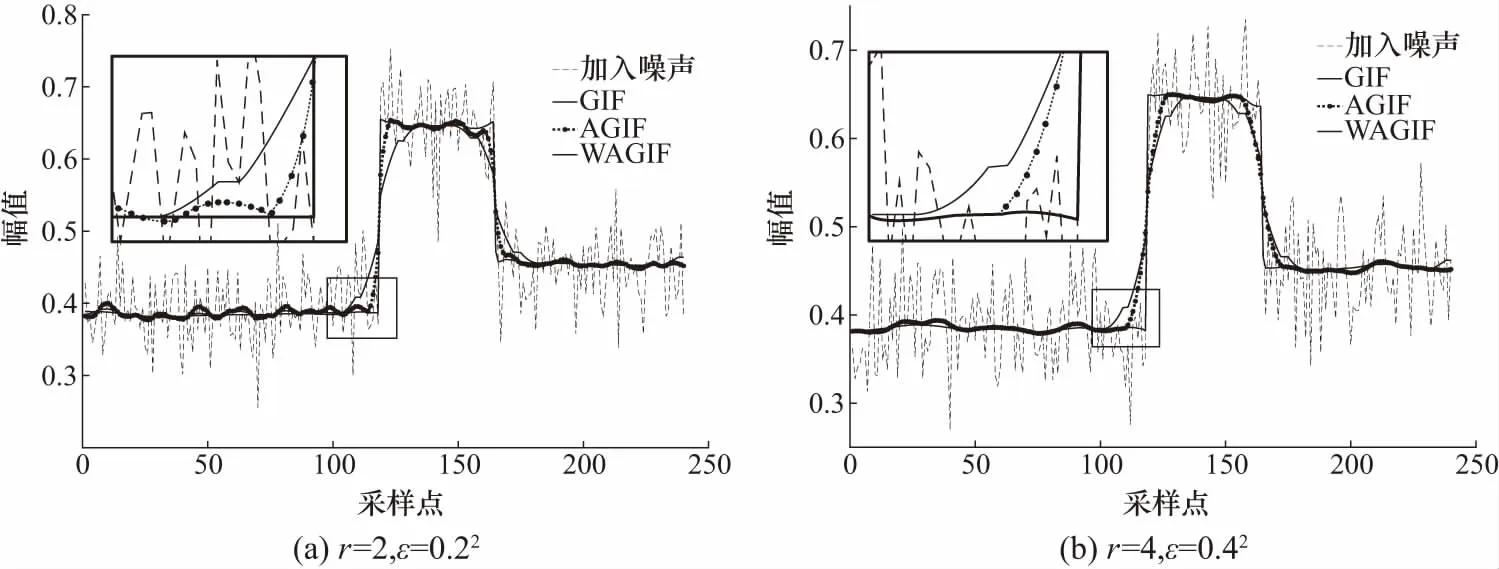
图6 不同r和ε下一维噪声信号的WAGIF滤波结果Fig.6 WAGIF filtering results for one-dimensional noise signals with different r and ε
图7展示了GIF与WAGIF作用于一维信号的细节对比. WAGIF在边缘处与真实值的差异较小,波形较为平缓,说明更接近真实值. WAGIF增强的波形更接近原始波形,GIF在边缘突变处产生较大误差.
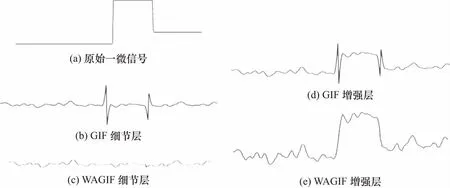
图7 GIF和WAGIF细节层和增强层对比Fig.7 Detail layer and enhancement layer comparison for WAGIF and GIF
需要说明的是,本文所有步骤均采用盒型滤波器boxfilter进行计算,计算复杂度没有额外增加,仍为O(N),其中N为图像的像素总数目.
3 实验与分析
下面分别从客观指标评价(PSNR、SSIM)和主观图像滤波效果两个方面,对WAGIF与目前经典滤波算法如高斯滤波(GF)、双边滤波(BF)、引导滤波(GIF)、梯度域引导滤波(GGIF)等开展对比实验. 实验环境Matlab2016,实验参数设置为:ε=0.22,r=2.
3.1 客观指标评价
选取TID2008图像数据集中25张图像,添加高斯噪声标准差分别为{2,4,6,8,10}. 表1显示了各滤波结果的PSNR均值. 在各级别的噪声情况下,由于GF算法、BF算法均采用高斯核进行平滑,两者的PSNR均值基本相当,GIF方法使用保边的线性约束,其PSNR均值相较于GF和BF有提升,GGIF方法基于一阶约束的方差设计权重,由于噪声的引入,容易将噪声视为边缘结构进行保留,因此PSNR均值在GIF的基础上并没有提升,反而下降,只相对于GF和BF略有提升,说明GGIF在处理有噪图像上效果并不十分理想. 本文方法能更准确地感知噪声图像的边缘纹理信息, PSNR均值有明显提升. 随着噪声的增大,各算法的PSNR值均有所下降,但本文算法PSNR均值仍然是各算法中最高的,所有级别噪声下PSNR均值提升率均在65%以上,最高接近70%. 即使在噪声标准差为6时,其PSNR均值比GF、BF和GGIF在标准差为2时都明显要高.
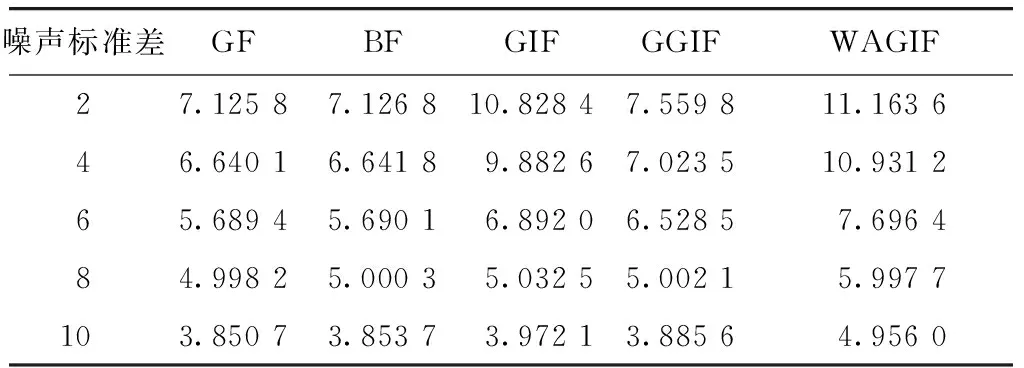
表1 各算法PSNR均值
表2为上述滤波算法的SSIM均值. 由表2可知,WAGIF的SSIM在不同噪声水平下都优于其他滤波器,对图像的结构保护效果更好.
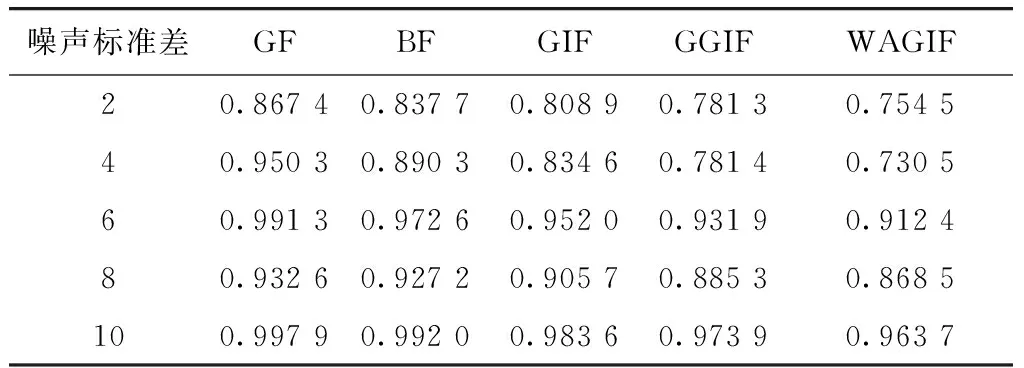
表2 不同噪声水平下各方法的SSIM均值
3.2 主观效果对比
针对纹理简单和复杂两类噪声图像进行滤波处理. 图像中加入方差为0.002高斯噪声.
图8纹理结构比较简单. GF和GIF方法去除部分小噪声,但图像边缘也相应模糊,GF去噪能力相对较弱,而GIF的边缘模糊更明显. BF方法能有效保留边缘,但大部分噪声并没有有效滤除. GGIF算法噪声滤除的效果最佳,且保边性能比GIF方法要好. 而WAGIF方法在最大程度保留图像边缘同时,较好地消除了平坦区域的噪声,处理效果明显优于其他方法.

图8 各种滤波器在纹理结构简单图片上的滤波结果Fig.8 Filtering results of simple context images
图9纹理较为复杂. GF结果中女孩脸上斑点明显被平滑,但是边缘模糊比较明显. BF算法结果中还能明显看到没有去除的斑点. GIF、GGIF算法相较于BF算法斑点平滑的效果有提升,其中GIF效果更好. WAGIF算法在更好去除女孩脸上斑点噪声的同时,眼睛处的细节也保留得较完好.

图9 各种滤波器在纹理复杂图片上滤波结果Fig.9 Filtering results of complex texture images
4 结 论
本文在引导滤波的基础上,分析了引导滤波固定的滤波参数存在的局限性,针对噪声图像,设计了一种基于峰度系数方差的边缘权重函数来有效感知图像的边缘. 然后在此基础上提出了一种新的加权自适应引导滤波算法,重点对自适应地调节正则化参数ε策略,聚合加权策略两个方面进行了改进. 实验结果表明,相较于几种经典的图像滤波算法,在主观测试和客观指标(PSNR、SSIM)等的验证下,本文方法在噪声平滑和边缘保持方面具有更好的性能.

