工艺参数优化下连杆摆动副衬套结构强度研究

向建华， 刘健， 钟乘龙， 魏满晖， 王宇江， 张利敏

(1. 北京理工大学 机械与车辆学院，北京 100081； 2. 中国北方发动机研究所，天津 300400)

由活塞、连杆、衬套和活塞销组成的连杆摆动副是内燃机中极易失效的部位，随着现代内燃机不断向着高功率方向发展，负荷逐步加剧，多场耦合作用不断增强，连杆摆动副的结构强度面临着巨大的挑战[1-2]. 而改善摆动副中最易失效部件衬套的使用性能则是改善连杆摆动副性能至关重要的一环. 研究表明，近1/3的衬套失效案例都与衬套加工有关[3]. 因此开展衬套加工工艺的相关研究对改善连杆摆动副的承载特性是很有必要的. 李正元等[4]研究了柴油机连杆衬套强力旋压加工中减薄率和热处理温度对某材料力学性能的影响. HUA等[5]建立了筒形工件三轮反向旋压的有限元模型，得出了其应力应变的分布情况，并通过实验验证了仿真结果. 樊文欣等[6]通过QSn7-0.2的强力旋压工艺实验，确定了衬套加工的最佳旋压工艺参数及退火温度. 以上研究通过仿真或实验的方式研究了工艺参数对衬套零件的力学性能的影响规律，但加工工艺参数对衬套在连杆摆动副组合工作下的结构强度影响及规律尚缺乏深入的研究.

1 衬套强力旋压过程的仿真分析

高功率内燃机对连杆摆动副衬套的力学性能具有很高的要求. 在实际生产中，由于强力旋压法具有加工条件简单、加工件力学性能较好等优点，因此强力旋压是最普遍的衬套加工方法[6]，其加工过程如图1所示. 加工过程中，芯模以一定速度旋转并依靠和胚料的摩擦力带动胚料旋转，旋轮作进给运动，使胚料连续地逐点变薄并贴靠芯模而形成衬套. 但另一方面，由于强力旋压过程中不均匀的塑性变形, 在旋压件内会产生残余应力, 残余应力的大小及其分布对衬套的使用性能产生较大影响，而进一步影响连杆摆动副中的结构刚强度特性[7-9].

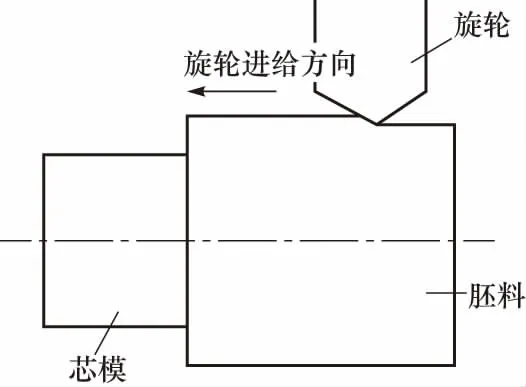
图1 旋压过程示意图Fig.1 Schematic diagram of spinning process

1.1 三旋轮错距强力旋压建模

文中研究的衬套利用abaqus建立三旋轮错距强力旋压模型如图2所示，具体参数如表1所示. 三个旋轮呈120°均匀分布，同时三轮之间存在一定的轴向和径向错距，以实现一定的减薄率，并防止芯模由于旋压力不均导致产生偏心现象. 考虑到文献[10]对旋压仿真过程中的力学相关的概念与内容已做陈述，且文中重点在于连杆摆动副中残余应力影响的研究，故此方面文中不再详细叙述. 同时，由于旋压过程中不均匀的塑性变形所产生的残余应力很大，故认为胚料中初始残余应力接近于0，不予考虑.

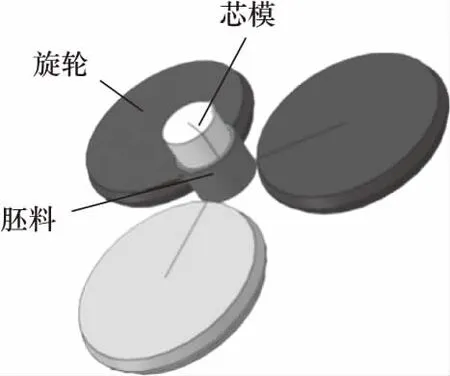
图2 三旋轮错距旋压几何模型Fig.2 Geometrical model of three-wheel staggered spinning

表1 模型尺寸Tab.1 Model dimensions

考虑到影响衬套加工残余应力的主要因素有强力旋压法中的减薄率φ、进给比f和主轴转速n以及后续热处理过程的温度T[7]，故文中主要以这几个因素来开展特性及影响规律研究. 建模时，由于芯模和旋轮的硬度和强度远大于胚料，故仿真分析中，芯模和旋轮被定义为解析刚体，只需定义胚料所采用锡青铜QSn7-0.2的材料属性如表2所示.

表2 QSn7-0.2材料属性Tab.2 QSn7-0.2 material attributes

而相应在网格处理时，采用六面体减缩积分单元C3D8R仅对胚料进行划分，同时考虑到胚料变形较大，设置ALE自适应网格控制以允许网格在胚料旋压过程中自适应调整形状. 在边界和载荷施加时，将芯模和胚料的上表面固定，进给运动和旋转都施加到旋轮上，通过相对运动达到和实际过程相同的效果.

1.2 衬套强力旋压结果分析

图3为芯模转速400 r/min、减薄率20%、进给比0.6时的衬套终旋阶段应力分布. 终旋阶段旋轮同衬套接触，上部因塑性变形最大，残余应力也达到最大，其值为416 MPa；应力以接触处为中心向周围扩散，接触处附近应力为200～300 MPa；在远离接触处的上表面，应力值小于100 MPa. 图4为旋压后衬套的等效塑性应变分布，由于大部分时间中圈部分同接触处较近，中圈部分形变量较大；上表面区域由于上表面的固定，应力集中，导致形变量最大，等效塑性应变值为4.56；下表面部分变形极小，仅在初旋阶段产生了微小变形.

图3 衬套终旋阶段及其应力分布Fig.3 The final rotation stage of bushing and its stress distribution

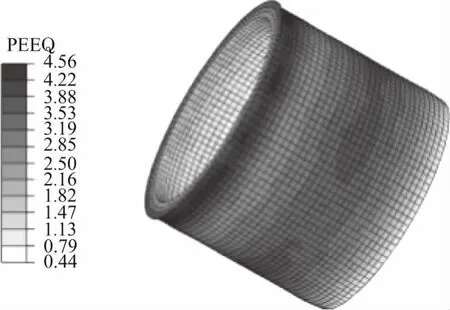
图4 衬套终旋后的等效塑性应变分布Fig.4 Equivalent plastic strain distribution of bushing after final rotation

表3为分别改变主轴转速、旋轮与芯模轴线的距离以及旋轮进给速度v与主轴转速n的比值来改变减薄率φ和进给比f，通过控制变量法实现对3个主要加工参数对残余应力分布和变形的影响规律. 不同减薄率、主轴转速、进给比对残余应力值影响不大，最大值为416 MPa左右，主要分布在旋轮进给的最终位置一侧；但这3个参数对等效塑性应变和最大变形影响较大，与旋压成型工艺的特点相符合，其中最大值分别为11.41和19.17 mm.

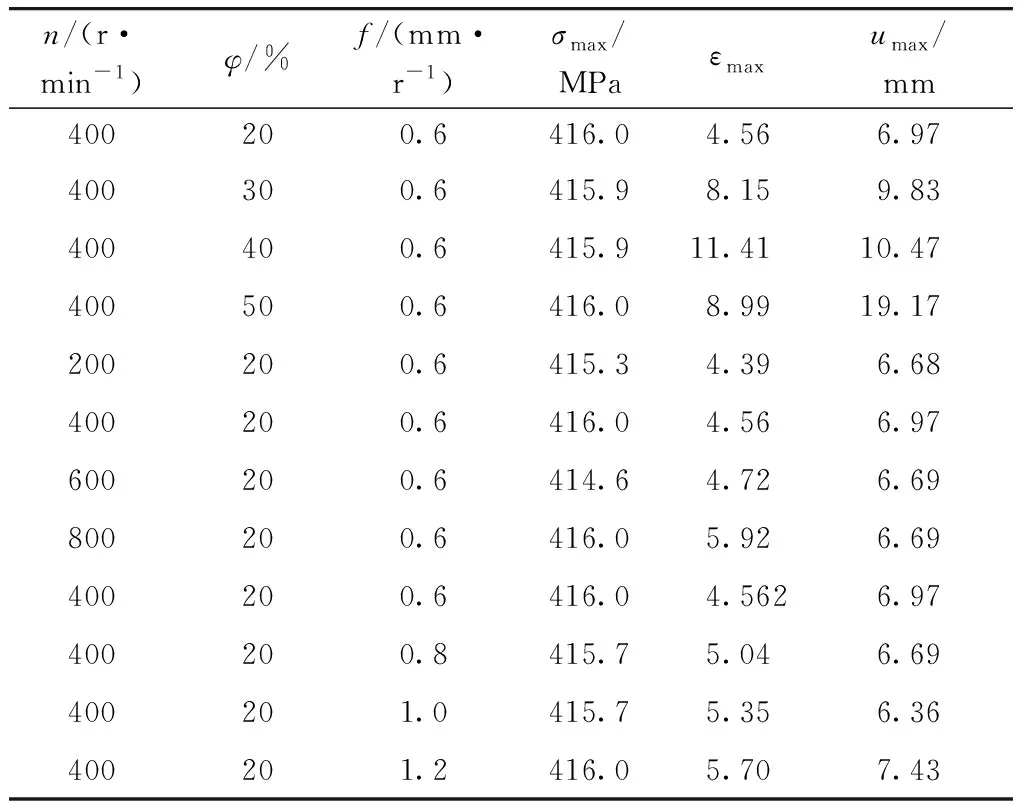
表3 不同参数下的仿真结果Tab.3 Simulation results in different parameters

2 考虑旋压工艺下的连杆摆动副结构强度分析

通过衬套强力旋压过程分析可以得到衬套残余应力的分布，还需进行热处理等工序才能得到成品，会进一步影响衬套的残余应力值. 此外，1.2中3个参数虽对最大应力影响不大，但减薄率、进给比对衬套力学性能有一定的影响.

李涛等[8]考虑旋压工艺参数和热处理温度，通过试验得到了屈服强度和抗拉强度关于减薄率、进给比和热处理温度的回归方程.

屈服强度的回归方程为

σ0.2=452.19+413.62z1-363.02z3+715.57z23

(1)

抗拉强度的回归方程为

σb=254.68+1 195.55z1+0.83z2+

206.16z3-3.21z1z2-180.47z23

(2)

式中：z1为减薄率；z2为热处理温度；z3为进给比.

在后面的仿真中，相关参数的设置采用式(1)和式(2)的回归方程.

2.1 衬套残余应力的模拟导入

衬套强力旋压后还需要通过热处理工序以进行应力退火，随着退火温度逐渐升高，残余应力消除效果逐渐明显. 根据文献[9]，本衬套产品取旋压后所得毛坯应力值的10%作为衬套最终残余应力.

对该应力场的模拟通过施加温度和设置热膨胀系数的方式,以形成相似的残余应力场(主要包括最大应力值的相似和应力分布的相似)，并直接导入衬套中，即实现了将最终衬套残余应力导入连杆摆动摩擦副模型中的目的. 图5是以290 ℃退火温度为例，模拟时在初始分析步中定义25 ℃的恒温度场，在静力分析步中将温度场升高到41 ℃，得到如图所示的等效残余应力场. 由于温度载荷均匀，边界约束对称，残余应力场具有高度对称性，最大应力值为42.3 MPa，和强力旋压仿真(图3b)并进行热处理后的应力值41.6 MPa接近，衬套同活塞销和连杆接触部分应力值较小，接近25 MPa，未接触部分应力值在35 MPa左右.

图5 等效残余应力场Fig.5 Equivalent residual stress field

2.2 连杆摆动副有限元建模

连杆小头衬套组合结构模型由活塞、活塞销、衬套和连杆四部分组成，如图6所示. 网格的划分采用C3D10四面体和C3D8R六面体网格结合的方式，该连杆摆动副有限元模型共包含1.451 44×105个实体单元、2.294 93×105个节点.

图6 连杆小头衬套摆动副有限元模型Fig.6 Finite element model of swing pair of connecting rod small end bushing

在边界条件方面，对连杆大头进行全约束，以固定整个模型；对活塞及活塞销轴向约束，以模拟活塞销卡簧轴向固定的作用；对活塞进行约束，以模拟气缸套导向作用. 此外，根据接触要求，活塞销与连杆衬套之间采用间隙配合，间隙量分别为0.03 mm；连杆小头与连杆衬套之间采用过盈配合，过盈量为0.04 mm. 接触关系均为剪切摩擦，连杆小头和连杆衬套、活塞销座和活塞衬套的摩擦系数为0.1，活塞销和连杆衬套、活塞销和活塞衬套的摩擦系数为0.07. 在施加载荷方面，对活塞顶部施加向下的气体爆发压力，约21.9 MPa；将曲柄连杆机构受到的往复惯性力以体积力形式加载，约2.18×108kg/(m2·s2)；将小头运动副所受的热载荷以该工况下相对稳定的温度场形式加载，分别设定为150 ℃的正常工作温度；而衬套的残余应力场的施加通过导入2.1部分获得的odb文件来实现.

2.3 连杆摆动副衬套结构刚强度分析

运用图6的有限元模型，并基于衬套强力旋压在转速400 r/min、减薄率20%、进给比0.3以及热处理温度290 ℃工艺参数下所形成的残余应力工况条件，开展连杆摆动副结构强度计算分析.

图7为连杆摆动副中衬套的应力分布，因衬套型线的结构设计，图7(a)和图7(b)应力呈现边缘低、接触区高、中间低的对称性分布，且可以看出，应力分布形态接近，考虑残余应力衬套最大值应力为459.32 MPa，相比不考虑大了43.2 MPa. 而从底部轴向应力分布图7(c)可看出，衬套承压接触处最大处差值约为40 MPa，其余部位应力差值约100 MPa. 这是由于考虑残余应力时温度应力增长速率较高,如图7(d)中0～1 s所示，在1 s时载荷加载抵消部分应力，整体应力值下降，而接触区压力较大，导致接触区应力不降反升，且不考虑残余应力时增速较快，所以有无残余应力影响时，接触区应力差值较中部小.

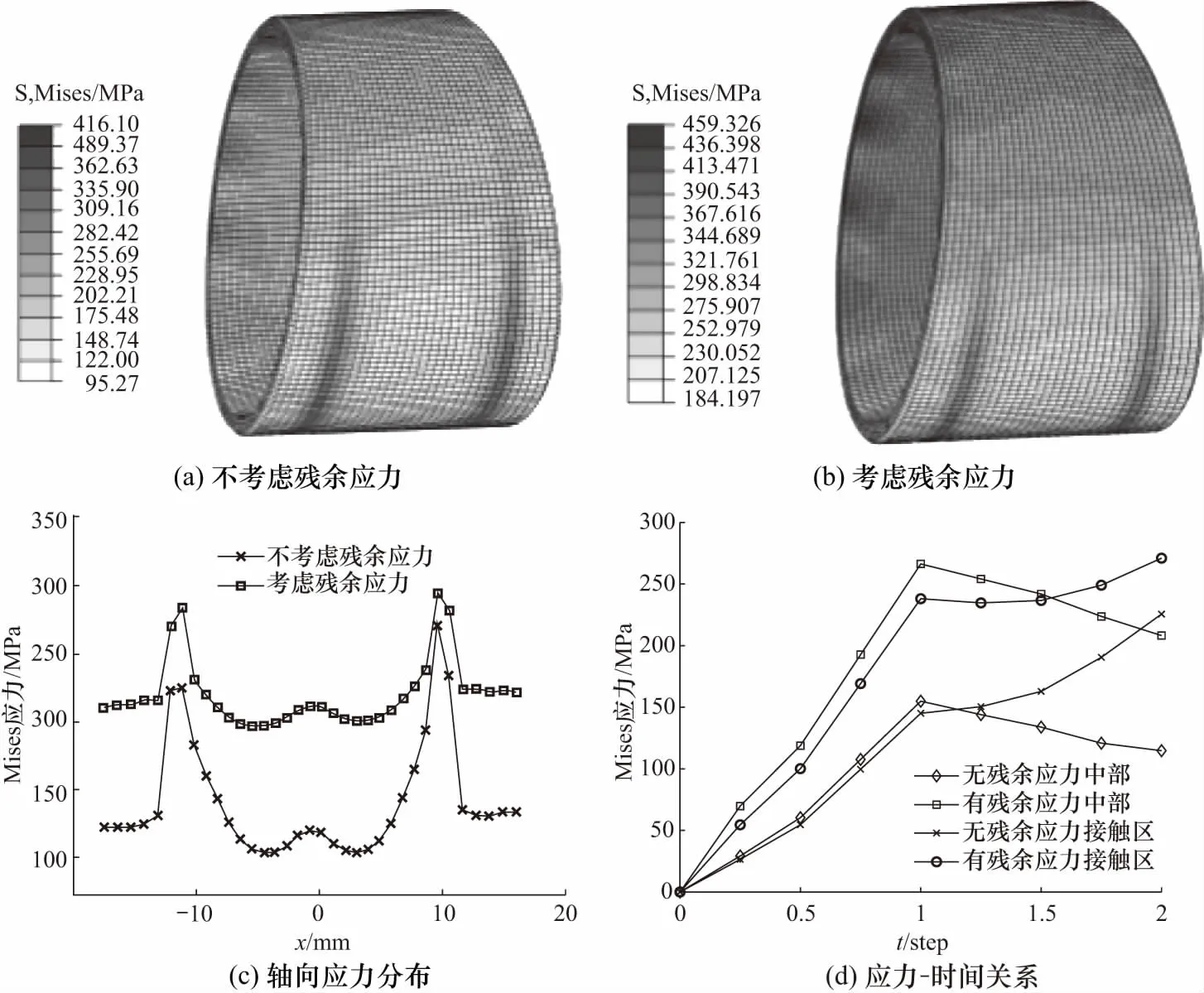
图7 连杆摆动副中衬套的应力分布Fig.7 Stress distribution of bushing in swinging pair of connecting rod

图8为连杆摆动副衬套的匹配接触应力分布，因边缘接触变形，接触应力整体呈现两边大中间小的趋势(最边缘因衬套有切削量，接触应力为0)；从图8(a)和图8(b)可看出，有无残余应力对接触压力基本没有影响；排除活塞销与衬套接触边沿网格尖点的影响，图8(c)显示匹配接触压力均为从150 MPa渐增至230 MPa左右. 图9为连杆摆动副衬套的位移分布，图9(a)和图9(b)变形沿轴向呈对称分布，考虑残余应力的最大位移变形为77.90 μm，且在边沿侧位移变形值较大. 图9(c)显示残余应力使得衬套变形量沿轴向差值增大约0～40 μm，相对变形量最大增加约一倍左右.

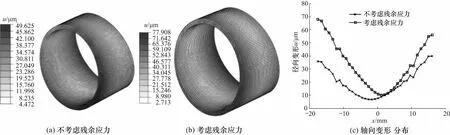
图9 连杆摆动副中衬套的位移分布Fig.9 Displacement distribution of bushing in swinging pair of connecting rod

3 工艺参数对连杆摆动副衬套结构强度影响分析与优化

衬套是连杆摆动摩擦副的易损部件，提高衬套工作下的刚强度可以极大地提高连杆摆动摩擦副的使用寿命. 从加工角度出发，强力旋压法中对衬套刚强度影响最大的工艺参数有减薄率、进给比和旋压后的热处理温度，为此本部分采用响应面BBD试验设计方法开展这些因素对连杆摆动摩擦副衬套强度的规律分析和优化研究.

3.1 响应面法模型建立

选用工艺参数减薄率、进给比和热处理温度等三个因素作为试验因子x1、x2、x3；其中减薄率取值20%～50%，进给比选取0.1 mm/r～0.5 mm/r，热处理温度取260 ℃～300 ℃. 衬套的失效多为变形导致的应力集中和接触失效，例如偏磨、衬套松动等；而由2.3的分析可知，加工参数并不影响衬套接触压力的分布，故选取衬套最大应力y1和衬套最大位移变形y2为响应变量. 得到的14组试验结果如表4所示.

采用Design-Expert软件对表3从低次模型开始进行拟合，构造出关于各响应变量的响应模型，并通过显著性分析得到响应面近似函数.

最大应力响应模型为

y1=57.211 96+6.231 14x1+

281.354 17x2+1.500 42x3-6.833 3x1x2-

(3)

最大位移响应面模型为

y2=-333.312 01+4.832 72x1+39.958 33x2+

2.177 5x3-2.259 17x1x2-0.019 78x1x3-

(4)

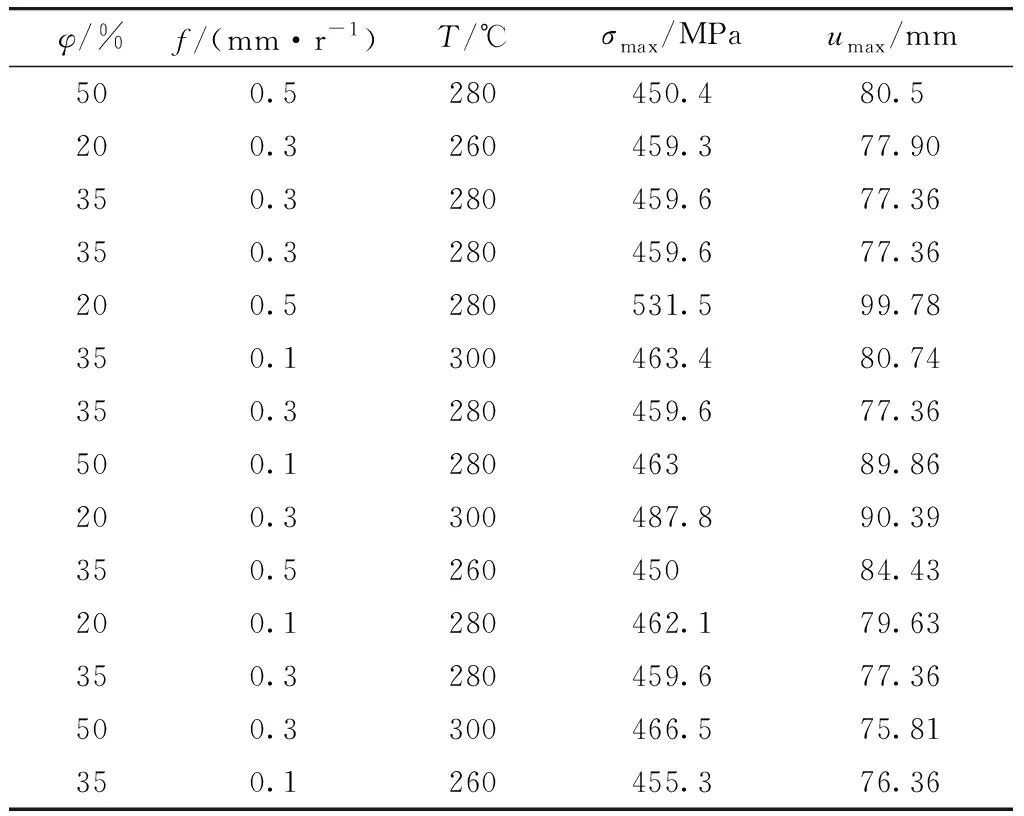
表4 试验数据结果Tab.4 Experiment results

3.2 工艺参数的影响规律研究

由式(3)和式(4)可以获得工艺参数减薄率、进给比和热处理温度对衬套最大应力和最大位移变形量的影响规律. 从图10的衬套工艺参数对最大应力的影响规律图中可以看出：随着减薄率的升高，衬套最大应力先减小，在42%减薄率处开始增加；随着进给比的增加，最大应力单调递增且增长速度稳定；随着热处理温度的升高，衬套最大应力增大，热处理温度对衬套最大应力的影响程度不及进给比. 从图11中衬套工艺参数对最大位移变形的影响规律图可以看出：随着减薄率的增大，衬套最大位移变形增大，但增加幅度很小，减薄率从20%增加到50%，衬套最大位移形变增幅不到10 μm；随着进给比增大，衬套最大位移形变增大；随着热处理温度的增加，衬套最大位移形变均匀增大，但影响程度不及进给比.

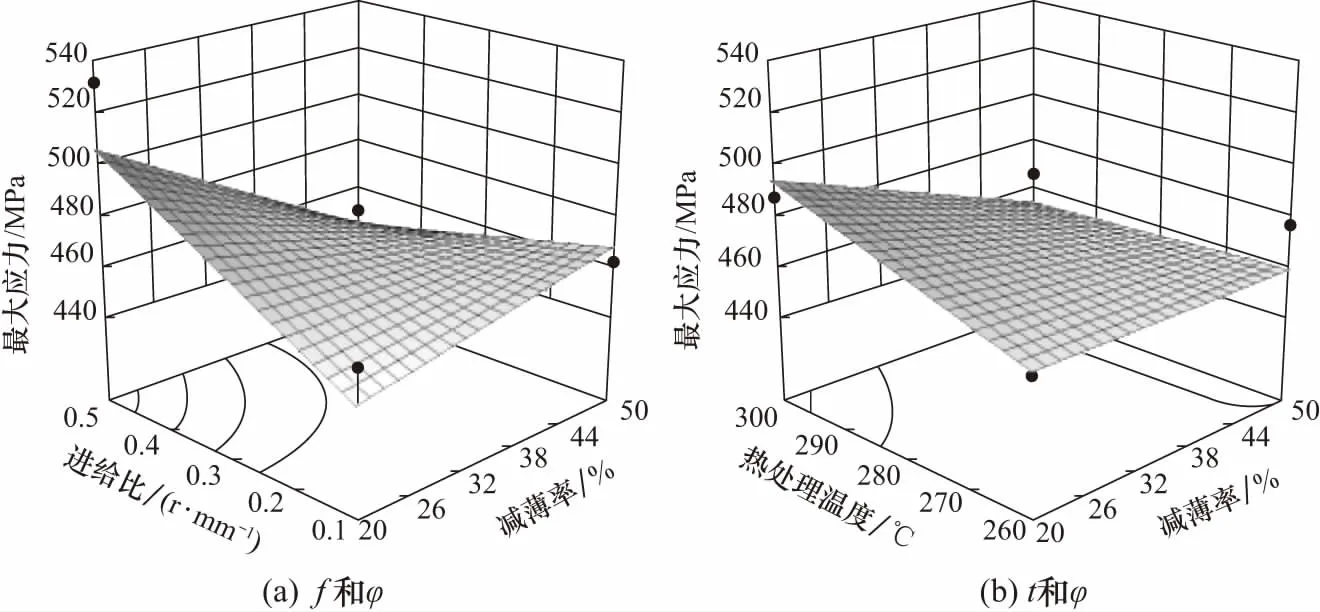
图10 衬套工艺参数对最大应力的影响规律Fig.10 Influence of bushing process parameters on maximum stress

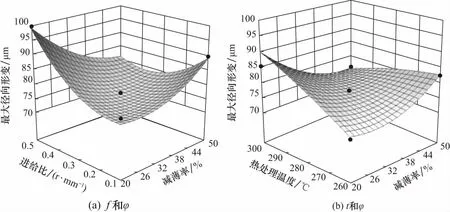
图11 衬套工艺参数对最大位移变形的影响规律Fig.11 Influence of bushing process parameters on maximum displacement and deformation

从图11中衬套工艺参数对最大位移变形的影响规律图可以看出：随着减薄率的增大，衬套最大位移变形增大，但增加幅度很小，减薄率从20%增加到50%，衬套最大位移形变增幅不到10 μm；随着进给比增大，衬套最大位移形变增大；随着热处理温度的增加，衬套最大位移形变均匀增大，但影响程度不及进给比.

3.3 工艺参数的优化设计

为了使连杆衬套在受压工况下的结构强度更加可靠，避免发生失效问题，需要确定连杆衬套的最优工艺方案. 根据3.1的模型对连杆衬套的机加参数及热处理温度进行优化设计，优化数学模型为

miny1

miny2

20% ≤x1≤ 50%

0.1≪x2≪0.5

260≪x3≪300

(5)

通过Design-expert优化求解得：减薄率为28.37%，进给比为0.154，热处理温度为261.73 ℃时，衬套最大应力和最大径向位移取得极小值，分别为445.01 MPa和71.99 μm. 该优化预测值和实际计算值(图12(a)应力云图的444.00 MPa和图12(b)的变形云图的74.38 μm)，误差分别为1%和3%.

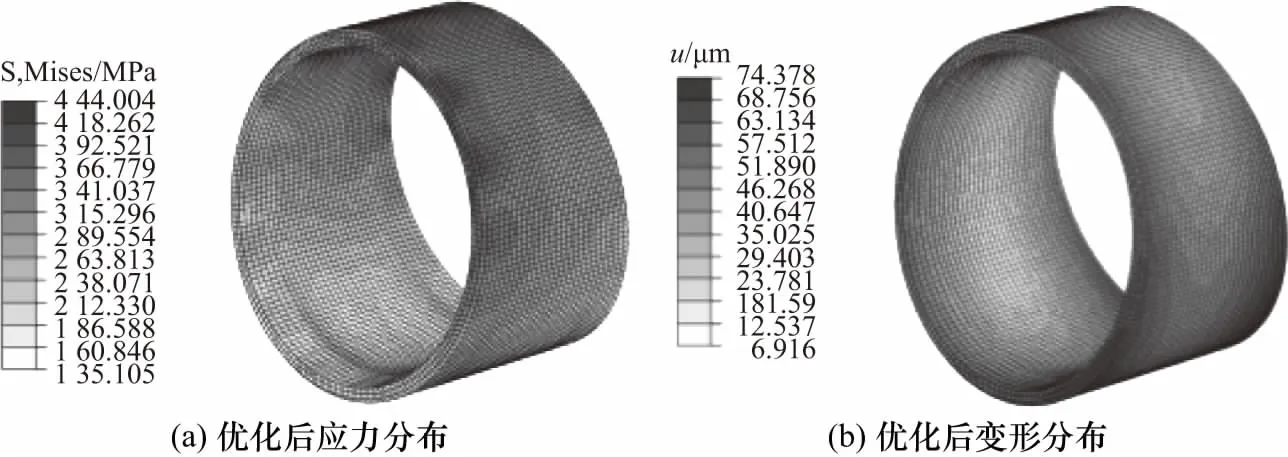
图12 衬套优化后的应力和变形分布Fig.12 Stress distribution anddeformation distribution of bushing after optimization

4 结束语

衬套的强力旋压参数减薄率、主轴转速、进给比对残余应力值影响不大，残余应力值沿轴向呈对称分布，且两端较大, 文中研究的衬套强力旋压后的残余应力最大值为416 MPa左右，并可通过等效温度场来模拟;在连杆摆动副中，残余应力会使连杆摆动副工作中的应力与变形增大，残余应力较大处增幅明显，而对接触压力影响较小;基于响应模型获得了工艺参数对连杆摆动副中衬套应力和变形的影响规律，并计算得到减薄率28.37%、进给比0.154和热处理温度261.73 ℃的最优工艺参数下，使得衬套最大应力和最大径向形变取得极小值，分别为445.01 MPa和71.99 μm.