大规模卫星集群网络自适应加权分簇算法

陈宇， 张勇，2， 陈实

(1. 中国科学院 国家空间科学中心，北京 100190； 2. 中国科学院大学 计算机科学与技术学院，北京 101408)

卫星通过模块间的无线链路实现复杂的信息交互进而完成相互间的协作，并最终构成分布式卫星集群系统，执行多样化的空间任务，已经成为未来卫星系统的重要发展趋势之一[1]. 随着卫星集群编队构型以及空间通信等技术的日渐成熟[2-3]，未来卫星集群系统的规模将越来越大，传统的平面式管理结构存在管理时延大、负载不均衡、可靠性低的缺点. 相比之下，采用分簇算法将整个网络转化为层级化的网络结构具有非常多的优势：有效利用多信道技术提高网络容量，优化节点带宽的利用；通过选取适当的节点作为簇首，有效减少网络中路由控制信息的开销，优化网络管理；屏蔽局部拓扑结构变化的影响，提高整体网络结构的稳定性；可随新节点的加入和任务需要而不断自我调整，具有良好的可拓展性.

现有的分簇算法大多是基于地面无线自组网提出的，并取得了完善的发展. 在此基础上，研究人员对应用于卫星网络的分簇算法进行了许多研究[4-8]，然而其大多是基于卫星星座提出的，网络拓扑相对固定. 在大规模卫星集群中，集群内卫星分布在相对距离几百米到几千米的范围内，网络结构比较灵活，且各卫星在一定范围内相互绕飞，网络拓扑不断发生改变[1]. 因此，本文提出了一种新型的自适应加权分簇算法，初始化由地面终端根据卫星集群网络的先验信息计算出加权权重划分簇首和成员节点，星上只运行簇的维护阶段，另外对节点入簇和状态改变的条件进行优化，以达到更好的负载均衡并且降低管理维护的开销.

1 总体设计

分簇算法根据系统要求将卫星集群划分成多个集合，理想情况下希望以最少的簇头覆盖整个网络[8]. 为了减少分簇算法带来的额外控制开销，提高网络容量的实际利用率，分簇算法应该尽量保证较低的算法复杂度. 此外，卫星集群网络中节点间的相对移动会导致簇内拓扑关系发生变化，严重情况下甚至会引起簇首节点更新以及网络重新配置，严重降低网络的性能. 因此，分簇算法应尽量保持原有的网络结构.

文中提出的大规模卫星集群自适应加权分簇算法以节点综合权值作为簇首选举及簇结构维护的重要依据，权值计算主要考虑了连接度、载荷服务能力以及优先级等因素，算法的基本工作步骤如图1所示. 为了减少分簇带来的额外开销，权值计算和初始化阶段由地面控制终端完成，星上只需要少量的通信和控制开销即可实时分布式地执行维护算法.

图1 分簇算法工作步骤Fig.1 Working steps of clustering algorithm

2 权值计算

分簇算法的核心是簇首节点的选取，本文中簇首的选取采用组合加权方式选择(节点权值越大，成为簇首节点的概率越高)，并考虑了卫星节点的特殊性对加权参数进行了选择和优化. 下面对本文中选取的加权参数进行介绍.

平均连接度α：节点i在一个周期内的平均连接度为

(1)

式中：T为卫星网络周期；θi表示节点i在周期中某一时刻的度(邻居节点的数量). 本文中为了简化仿真，将周期划分为多个时间片，假定时间片内网络的拓扑不发生改变，因此时间片t内网络的拓扑关系可以用邻接矩阵At来表示，则公式(1)转化为公式(2).

(2)

式中：N为划分的时间片的数量；θi(t)表示在第t个时间片内节点i的度数；aij为1表示第t个时间片节点i和节点j相连，aij为0则表示第t个时间片节点i和节点j不相连.

载荷服务能力ρ表示了卫星节点有效载荷的最大服务能力，例如：星上存储、计算能力、传输带宽与通信范围等等. 载荷服务能力ρ为由卫星节点本身能力决定的.

考虑到某些任务需求，一些节点可能会被给予更大的期望担当簇首节点，因此设定簇首优先级φ∈[0,1]，即优先级越高，节点担当簇首节点的概率越高，反之节点担当簇首节点的概率越低.

最后，对于网络中的每个节点v，其权值wv计算公式为

wv=(w1α+w2ρ)φ

(3)

其中系数w1和w2为相应参数的加权因子，满足w1+w2=1，具体值由地面终端根据需要预先设定.

3 分簇算法

本文提出的ADWCA分簇算法分为两个阶段：簇的初始化和维持阶段. 其中，初始化阶段由地面终端完成，主要任务是在初始时刻划分所有节点状态，指定适当的节点担当簇首节点. 簇的维护阶段负责在集群网络拓扑发生变化时，对簇结构进行维护，确保所有节点均在簇结构中. 分簇过程中，将节点状态分为4种：簇首(cluster head ,CH)、普通成员、未定状态和游离状态. 初始时所有节点状态均为未定. 下面对初始化和维护阶段进行详细说明.

3.1 初始化阶段

初始化阶段工作主要由地面终端完成，地面终端根据集群信息和上述权值公式计算出各个节点的权重后，划分节点状态，过程如下所示.

1) 根据初始时刻邻接矩阵判定节点是否存在邻居节点，若不存在，则将该节点划分为游离状态. 否则，进入下一步，此时节点为未定状态.

2) 查找节点的k跳邻居节点中是否存在簇首CH节点，若存在，则按公式(4)计算优先级最大的CH加入，节点状态划分为普通成员. 若不存在CH，则进入下一步.

(4)

式中：p(i,CHv)表示节点i加入簇首v的优先级度量；wv表示簇首节点v的权重；s表示簇内节点数量；h表示节点i距簇首节点v的跳数.

3) 比较节点自身权值和k跳内邻居中所有未定节点权值，若节点自身权值为最大值，则将节点划分为簇首节点，簇内节点数量初始化为1，否则返回上一步.

初始化过程可能需经过多次迭代，直到所有节点状态均确定，算法流程图如图2所示.

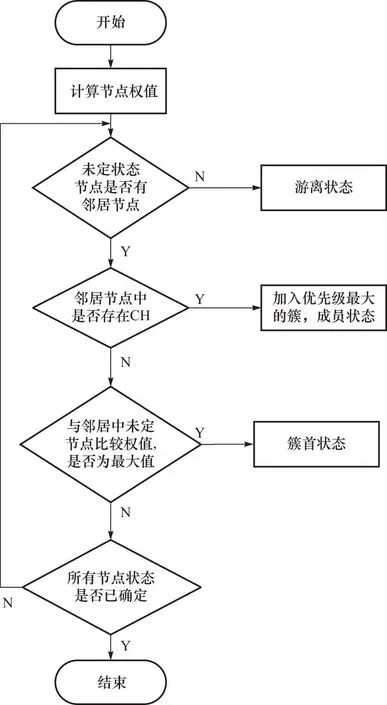
图2 初始化算法流程图Fig.2 Initialization algorithm flow diagram

3.2 维护阶段

初始化阶段完成后，卫星集群网络立刻进入簇维护阶段，各节点通过一定的信息交互(大部分发生在簇内)完成自身的状态变化，节点状态改变主要分为以下4种.

① 簇首节点状态变化：一般情况下，簇首节点状态不会发生变化. 当簇首节点不存在邻居节点时，转变为游离状态. 另一方面，考虑到负载均衡，当簇内节点数量超过一定时限始终为一时，簇首节点退化为未定状态.

② 簇成员节点状态变化：成员节点判断自身与原簇首节点之间即将断开连接或跳数大于k跳时，开始计时，超过一定时限向原簇首节点发送离簇申请，并检索是否有邻居节点，若没有邻居节点，则转变为游离状态，否则转变为未定状态. 本文中，设定成员节点大于或等于两个时间片仍与簇首断开连接时发生状态改变.

③ 游离节点状态变化：游离节点发现自身与其它节点存在连接时，转换为未定状态.

④ 未定节点状态变化：未定状态作为一种临时态，节点在未定状态不停留，需要立即转变为成员状态或簇首. 转变规则如下：检索其k跳邻居内是否存在CH，若存在则按照公式(4)计算并选择优先级最大的CH加入，节点状态转换为普通成员状态. 若其k跳邻居内不存在CH，且自身权值最大，则该节点成为簇首.

维护阶段节点状态转换图如图3所示.

图3 维护阶段节点状态转换图Fig.3 Node state transition diagram during maintenance phase

4 仿真与分析

衡量一个分簇算法的优劣主要有以下几个标准：簇首节点的数量、簇结构的稳定性和负载均衡度等. 本文采用MATLAB软件对ADWCA算法在大规模集群卫星网络中的性能进行了仿真，并与最小标识分簇算法(lowest-ID algorithm,LID)和最大连接度优先算法(highest-connectivity degree algorithm,HCC)进行了比较. 仿真实验参数如表1所示. 为了降低单次实验的随机性干扰，最终结果取20次仿真结果的均值.

表1 仿真参数Tab.1 Simulation parameter

在链路容量允许的情况下，簇首节点数目少的算法能够有效提高链路的利用率. 但由于星上载荷能力的限制，单个卫星节点不可能服务所有k跳内邻居卫星节点，因此需要对簇成员的数量作出一定限制. 本文仿真中假定簇内节点最大数量为10个，即生成的簇结构内簇首数量至少为20个. 图4反映了3种算法在仿真期间建立的簇结构的簇首数量，从图中可以看出，本文ADWCA算法所生成的簇首数量在整个仿真期间更少且更稳定，明显优于LID和HCC算法.

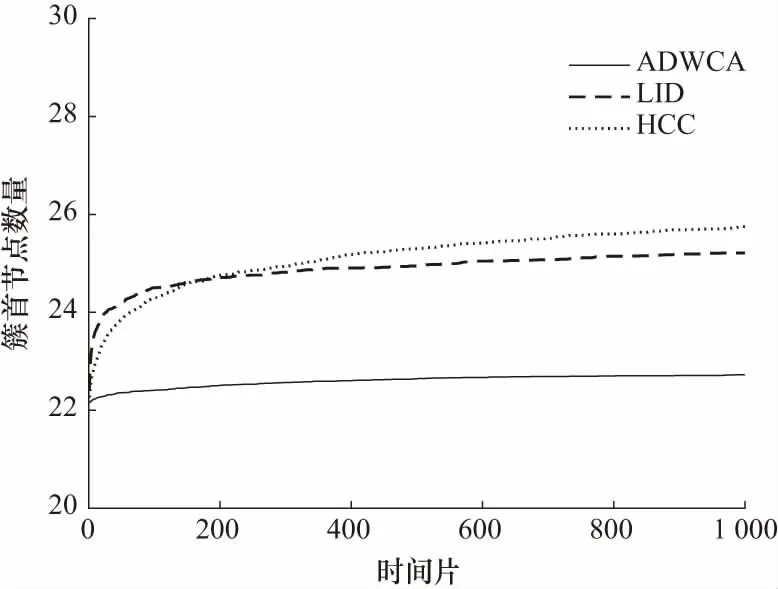
图4 簇首数量对比Fig.4 Comparison of the number of cluster heads

簇结构的稳定性采用节点状态变化次数来度量，即每个时间片内所有节点发生状态变化的总次数. 变化次数越少，说明簇的稳定性越高，控制开销就越低. 图5反映了仿真期间3种算法在各个时间片发生状态变化的总次数. LID和HCC算法发生状态变化的次数在取多次仿真结果的均值后是非常接近的，大概在每个时间片90次左右. 这是因为仿真中采用的是随机生成的拓扑，且LID和HCC算法节点发生状态改变的条件几乎一致，另外考虑到簇首节点的状态不轻易发生变化，仿真结果是满足预期的. 而ADWCA算法的节点状态改变次数则只有45次左右，下降了一半的数量，极大地提高了簇结构的稳定性.

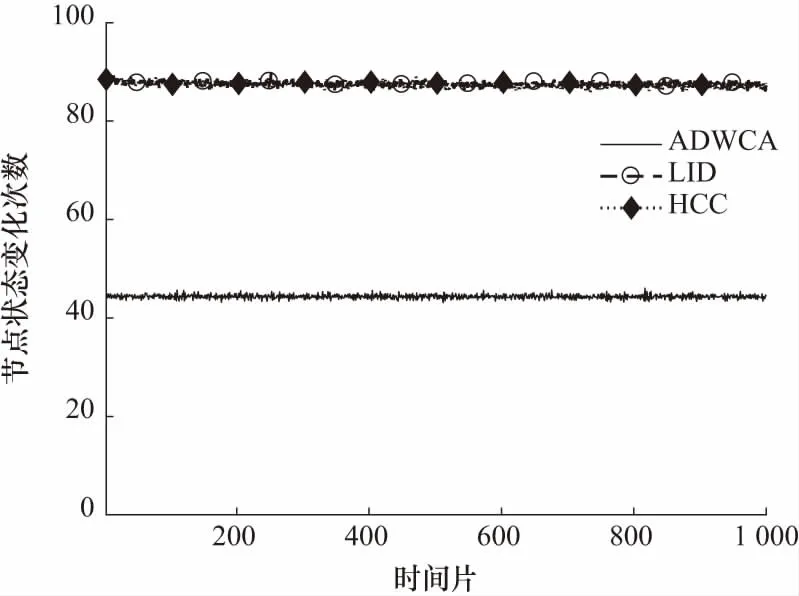
图5 节点状态变化次数对比Fig.5 Comparison of the number of node status changes

簇首的负载大小取决于其所支持的节点的多少. 簇结构的维护和基于分簇的路由均需要消耗簇首一定的资源，因此不希望出现有的簇首过载，有的簇首却很轻闲的状况. 本文采用文献[9]提出的负载均衡度(load balance factor,LBF)的概念作为量化指标,具体计算如公式(5)所示.

(5)

式中：xi为簇首节点i的成员节点数；u为簇首的平均邻居节点数量，u=(N-nc)/nc，N为网络中的节点数，nc为簇首节点的数量. 该值越大，表示负载均衡度越好.

图6反映了整个仿真期间3种算法负载均衡度的比较，从图6中可以看出，LID算法只以节点ID作为簇首的选举标准，没有考虑其他因素，负载均衡度在整个仿真期间最低. HCC算法以节点度数作为选举标准，负载均衡度较LID有所改善. 本文提出的ADWCA算法负载均衡度较前两种算法有了非常明显的提高，这是因为ADWCA分簇算法在节点入簇上做出了改进，综合考虑了节点距簇首的跳数、簇首权重以及簇内节点数量，当簇内节点数过多时，其新加入节点的概率就会减小. 通过这种方式平均各个簇内节点的数量，达到有效的负载均衡.

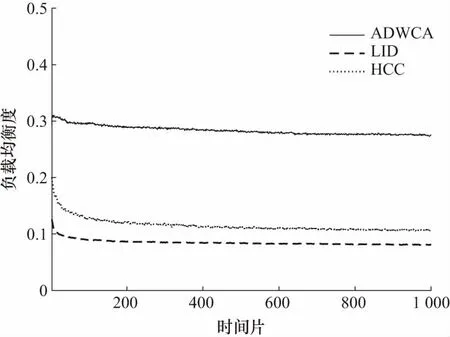
图6 负载均衡度对比Fig.6 Comparison of the load balance

5 结束语

大规模卫星集群网络相比于传统卫星星座动态性更强，同时面临着日益复杂的任务需求，采用分簇算法对集群网络进行分层式管理具有重要的意义. 本文提出了一种自适应分布式的分簇算法，由地面终端根据先验信息进行初始化分簇，星上通过实时的信息交互完成簇结构的维护，同时改进了节点入簇和状态改变的条件. 仿真结果表明，该算法生成的簇结构簇首数量更少，具有良好的稳定性同时能够达到有效的负载均衡. 但本算法也具有一些不足，例如没有考虑到卫星之间可能存在单向链路的情况，需要在下一步研究工作中继续完善.