基于深度学习理念的高中数学课前研习作业设计

朱云生

（福州第十八中学，福建 福州 350001）

《普通高中数学课程标准（2017 年版2020 年修订）》强调学生学科核心素养和解决问题的能力，需要引领学生向深度学习发展。单靠课堂上的师生协作学习，不足以达到深度学习的目标，因此学生的自我学习显得更为重要。笔者认为，以学生能力层次为基准，设计一份优质的课前研习作业，引导学生主动进行研究性学习，加上与之对应的有效课堂混合学习模式，便能满足学生的高阶思维能力需求，达到深度学习的目的。

一、设计理念与设计方向

课程标准对学与教提出了两条基本理念：1.学生发展为本，立德树人，提升素养；2.把握数学本质，启发思考，改进教学。依此可将课前研习作业的设计理念定为：以提升学生数学学科素养为目的，启发学生思考，探寻数学本质，导引课堂教学，为学生进入深度学习做铺垫。将培养数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六大核心素养作为设计方向。根据美国实证主义心理学家桑代克提出的著名的联结学说中得出的三条学习定律：准备律、练习律与效果律，将课前研习作业分两个部分设计，即自我探索研习新知和自纠练习引发思考。

二、自我探索研习新知设计

高中数学因学习目的不同，常见的有三种课型：新概念型课、探究发现型课和复习延伸课。不同的课型，课前研习作业也应区分设计。

（一）新概念型课自我探索研习设计：情境阅读+设问寻解

新概念课主要培养学生的数学抽象核心素养，在这种课型下，学生在学习过程中需要了解每个数学概念的产生背景，思考并解答以下三个问题：为什么要学这个概念？这个概念是哪里来的？它的形成过程是怎样的？这就构成了该课型课前研习作业的主体思路，设计上重在让学生学会阅读和寻找答案。教师需要选取适当的阅读材料提供给学生，其中课本教材是个很好的选择，几乎每个新概念课前都会有一部分阅读材料，可揭示三个问题的答案。但由于阅读量大而耗时，传统数学教与学又重结果轻过程，现实中大多数学生和教师都做了选择性跳过，学生素养得不到培养，更是无法进入深度学习，导致在新高考理念的试卷中，学生失分较多。这个过程适合放到课前研习作业里来完成。设计时可以采用提问式引入，作业的开篇即抛出一个实际问题，重点抛出，引起学生兴趣，促动学生思考如何寻求答案。但只有动力和兴趣，没有探索的途径和方法，学生在自学过程中极易受挫放弃。因此这部分需为不同层次的学生注明寻求答案的方法：对于程度不好的学生，可以为其指明答案在课本的大致位置，通过阅读即可解答。对于程度好的学生，鼓励其自主选择探寻答案的方式，例如查阅文献、上网搜索等。

［案例1］在《6.2.1 向量的加法运算》的课前研习作业中，可以做如下设计（参阅必修二课本P6-9）：

请先回顾向量的定义，思考以下几个问题。

如图：甲乙两同学在游乐场游玩，他们现在在A点，都想玩C点的游戏，只是甲想先去B点游玩。

1.甲乙两同学所走的位移能否用我们所学过的向量表示？

2.从最终的结果上来看，甲同学的位移和与乙同学的位移有什么关系？你能写出对应向量的结论吗？

3.从这个例子当中我们可以看出，向量的加法的结果是什么？

它可以怎样运算？请用你自己的话来阐述你得出的算法。

4.向量的加法还有其他算法吗？请你画图说明。

美国著名认知派心理学家和教育家布鲁纳在他的认知结构学习理论里主张学生的发现学习，本例即按照此理论设计。该设计让学生既能回顾旧知，又能学会探索新知，更重要的是能体验数学概念生成的过程，启发数学思维。问题4 设计为开放性问题，一般解答都在课本中，对于有探究能力的学生，他可以通过各种渠道搜索出课本之外的知识，此题成为其展现学习能力的舞台。解答上，要求学生不论对错，都要把自己的理解写出来。评价上，只要是学生经过思考得出的解答，教师都给予一定的认可，同时提出自己的建议。学生在得到教师的肯定后会产生较大的成就感，在之后课堂的学习中动力和效率就会提高，为教师组织学生进入更深层次的学习奠定基础。

（二）探究发现型课自我探索研习设计：引导探究+归纳结论

此课型主要培养学生逻辑推理的核心素养，其中归纳猜想注重知识的积累，需要见多识广。学生则要在探究过程中学会模仿和迁移。因此这种课型的课前研习作业建议从探究实例出发，将本节课需要学习的结论进行简化或实例化，利用一至两个例子将探究过程展示给学生，探究过程添加文字注释，让探究能力弱的学生也能看得懂。

这里需要引起重视的是，传统数学教学的模式导致部分学生只注重结论及解题应用，不关心结论产生的过程。仅仅设计阅读范例让学生阅读，可能的结果是学生不关注阅读，直接翻开课本找结论做题。这样会使该课前研习作业的设计变得毫无意义，学生逻辑推理的学科素养仍然得不到提升。为避免此情况发生，可在例题的展示过程中将关键步骤中一些不影响学习归纳的部分改为填空，让学生只有看了才会填，填了就明白。

［案例2］在《导数的几何意义》课前研习作业的探究部分可以设计如下：

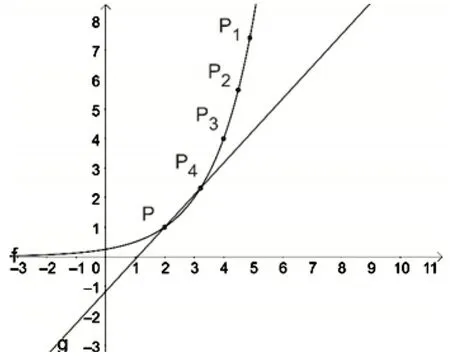
请同学们动手画图，并回答以下问题：

1.当点Pn（n=1，2，3，4）沿着曲线f(x)趋近点P时，割线PPn的变化趋势是什么？

2.当Pn向P逐步逼近的时候你发现了什么？

归纳出曲线的切线的定义:

当Pn→_______时，割线PPn→（确定位置）PT，PT叫做曲线________的切线。

3.割线PPn的斜率kn与切线PT的斜率k有什么关系呢？

当点Pn无限趋近于点P时，kPPn无限趋近于____。

4.函数f(x)在x=x0处的导数是切线PT的斜率k.即k==________。

该设计中的实例将课本中的知识探究过程具体化，课本中无标准解答，仅有结论。只有通过自己绘图尝试过后才能回答这几个问题。寻求解答的过程也是学习探究方法的过程——发现问题和提出命题，探索和表述论证的过程。这对培养学生逻辑推理核心素养有较大帮助。

（三）复习延伸课自我探索研习设计：思维导图+创题解答

复习延伸课一般都安排在章末或考试前，高三复习课程以这种课型为主。此时的学生已经掌握了大部分知识，只是有少许遗忘，这个阶段的知识研习设计应以鼓励引导学生完成知识的归纳总结为主。建议以表格填空形式或者思维导图形式展现给学生，学生通过完成填空，达到知识的回顾目的及知识体系的自我构建。

只是知识复习不能真正达到课前研习的目的，教师应认真筛选需要填空的部分，需要填空的必须是学生遗忘率及错误率高的部分。其中的高频考点，要求学生找出一题对应习题，在研习作业里完成解答。对于程度好的学生，可以要求他们自编或改编题。这个找题、编题的过程就是学生进行深度学习的过程。

三、自纠练习引发思考设计

（一）自纠练习设计：精题对比反思

知识研习后紧跟着的是自纠练习。桑代克认为简单机械的重复不会造成学习的进步，告诉学习者练习正确或错误的信息，有利于学习者在学习中不断纠正自己的学习内容。课前研习作业的自纠练习应以简单知识应用的易错题为主，习题形式要根据学生在研习时容易产生的错误命制。为了让学生能够发现问题，建议设计为对比练习，让学生在相似题中找不同，学生目的性明确、研习效果会明显提升。

［案例3］《1.5.2 全称量词和存在量词命题的否定》的自纠练习前半部分设计如下：

请同学们完成以下练习，想想这两题的命题的否定有什么不同？

1.写出下列命题的否定

（1）等腰三角形两腰相等

（2）∀x∈R,x2＞0

2.写出下列命题的否定

（1）等边三角形三边相等

（2）∃x∈R,＞0

两题相似度很高，对比关系明显，且要求学生探索不同。第1 题是对研习的简单实践，学生可以轻松应对。第2 题考查学生是否真正理解“否定”的意义，未能掌握的学生会跟解答第1 题一样改个句式解决。但如此完成此练习，明显不符合题目的要求。这样即可促使学生反思自己的解答，重新审视之前的自我研习过程。解答第2 题的关键是理解“否定”是对原命题结论的“全盘否定”，是要找出原结论反面的所有可能。因此2（1）的错解是“等边三角形三边不相等”。正解是“存在等边三角形，三边不全相等”同。样，1（2）的否定是“∃x∈R,x2≤0”，只需改变句式即可。不深入思考，2（2）就易得错解“∀x∈R,≤0”，然而原命题中的“＞0”默认包含“x-1 ≠0”。正解应是“∀x∈R,≤0 或x-1=0”。

这样的设计改变了以往数学低效的机械重复练习模式，用最少的题目让学生掌握了应有的知识。学生在这个过程中也能体会到正确的数学学习方法。

（二）引发思考设计：反思问题串+拓展应用问

只是单纯对比的自纠练习，无法要求所有学生都做出正确的反思和解答。因此引导学生进入思考的问题就很有必要了。

［案例4］前例自纠练习的后半部分可以这样设计：

1.请根据你自己的理解回答：命题的否定仅是命题形式上的改变吗？否定的是什么？为什么全称量词命题和存在量词命题的否定需要将∀和∃互换？

2.请你自编一个命题，写出该命题的否定，并以此为例说明下你对“否定”的理解。

第二题的问题串，意在为学生指明思路。学生通过思考这些问题，就能很自然地进入学习反思。回答完问题，也就会重新审视第一题的解答。在此之后设计若干思考拓展的问题，可以提升学习层次。第三题即为应用拓展，只有做到真正的理解才能举出合适的例子。

不同知识的思考拓展问题并不相同，新概念型课的拓展问题可以是“通过课前研习，你明白了什么？你能举个实例吗？”探究型课的拓展问题可以是“给你一个权力，去掉前面那题的一个条件，你觉得结果会产生变化吗？如果会，请说明如何变化；如果不会，请验证它”。复习延伸课可以是“请做思考：学完这些，你觉得你能解决什么样的问题？”思考并回答此类问题的过程本身就是深度学习的过程，而学生通过这样的练习可以检验自己的研习成效，若能利用家校互动学习平台与教师进行课前互动，及时获取反馈，纠正错误，达到足够的数学思维锻炼，更能事半功倍。