一个Hilbert型不等式的一般形式

有名辉，孙 霞

(浙江机电职业技术学院数学教研室，浙江 杭州 310053)

0 引言

定义加权赋范线性空间Lp,μ(X)如下：

其中p≥1，μ(x)在X上非负可测.若μ(x)=1，记 ‖f‖p,μ= ‖f‖p，Lp,μ(X)=Lp(X).若f(x),g(y)≥0，且f(x),g(y)∈L2(+)，则有

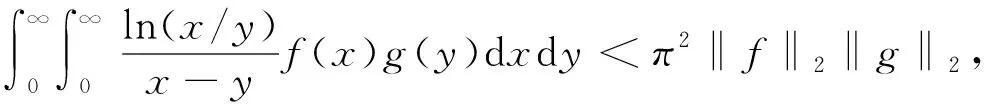
(1)

其中π2是满足式(1)的最佳常数因子[1].不等式(1)通常被称为Hilbert型不等式.Hilbert型不等式形式多样，技巧多变，100多年来一直是数学研究者热衷的研究对象.特别是20世纪90年代以来，以杨必成、洪勇、Krnic、Pecaric等为代表的学者通过不断创新核函数、改进系数、探究高维推广和算子表示及参数的等价条件，构建了大量形式精巧的新型Hilbert型不等式[2-8].这些不等式的创立借助了许多经典分析的技巧，同时也在一定程度上促进了分析学的发展.

2008年，杨必成[9]研究了式(1)类似的情形，建立了下列不等式：

(2)

其中C0=0.915 9…为Catalan常数.

2011年，周昱等[10]又建立了一个类似于式(2)且与Euler数相关的不等式，即

(3)

其中En(n∈)是Euler数，即E0=1,E1=1,E2=5,E3=61,….

式(1)、(2)及式(3)相关的推广和类比可参考文献[11-13].在此，通过构造一个一般形态的核函数，推广式(3)中的结果，同时给出一些新的特殊形态的不等式.

1 预备知识

引理1[14]设λ,a,b>0，且a+b=λ，n∈，Φ(x)=cscx，则

(4)

引理2设0<γ<1，且n∈，Φ(x)=cscx,则

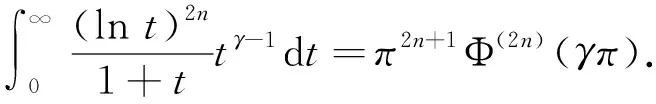
(5)

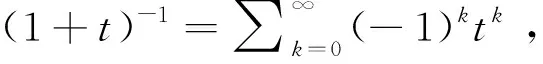
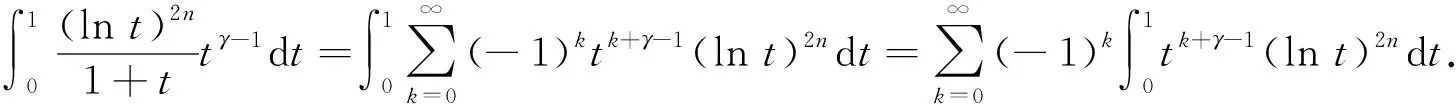
(6)

作代换lnt=-(k+γ)-1u，则有

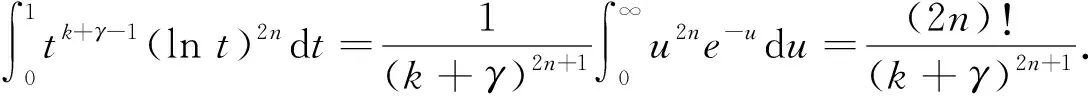
(7)

把式(7)代入到式(6)，可得

(8)

令t=1/u，类似可算得

(9)

结合式(8)和(9)，并利用式(4)，可得式(5).

引理3设p>1，1/p+1/q=1，γ1,γ2∈，且γ1γ2≠0.另有0<γ<1，n∈，且Φ(x)=cscx.设u∶Ω1=(a,b)→+及v∶Ω2=(c,d)→+严格单调递增可微，且u(a+0)=v(c+0)=0，u(b-0)=u(d-0)=+∞.设

φ1(x)=[u(x)]p(1-γγ1)-1[u′(x)]1-p，φ2(y)=[v(y)]q(1-γγ2)-1[v′(y)]1-q.

函数fm(x)和gm(y)(m为充分大的自然数)定义如下：

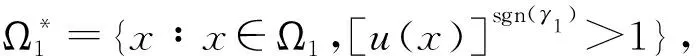
则当m→∞时，有

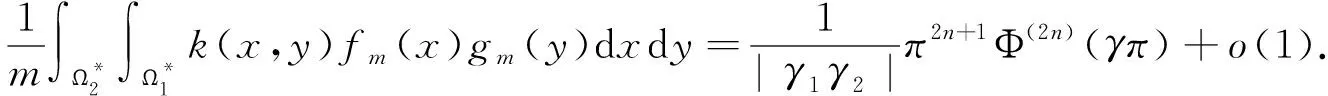
(10)

证明令uγ1(x)vγ2(y)=t，当γ1>0或γ1<0时，均有

当γ2>0或γ2<0时，又可算得

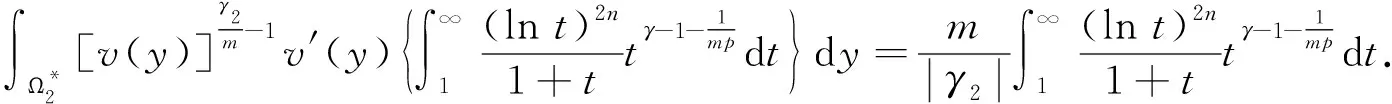
(12)

此外，通过交换积分的顺序，还可算得

(13)

将式(12)和(13)代入到式(11)，可得

令m→∞，由勒贝格控制收敛定理，并结合式(5)，便可得式(10).

2 主要结果

定理1设p>1，1/p+1/q=1，γ1,γ2∈，且γ1γ2≠0.另有0<γ<1，n∈，且Φ(x)=cscx.设u∶Ω1=(a,b)→+及v∶Ω2=(c,d)→+严格单调递增可微，且u(a+0)=v(c+0)=0，u(b-0)=u(d-0)=+∞.设

φ1(x)=[u(x)]p(1-γγ1)-1[u′(x)]1-p，φ2(y)=[v(y)]q(1-γγ2)-1[v′(y)]1-q.

f(x),g(y)≥0，且f(x)∈Lp,φ1(Ω1)，g(y)∈Lq,φ2(Ω2).k(x,y)由引理3定义，则

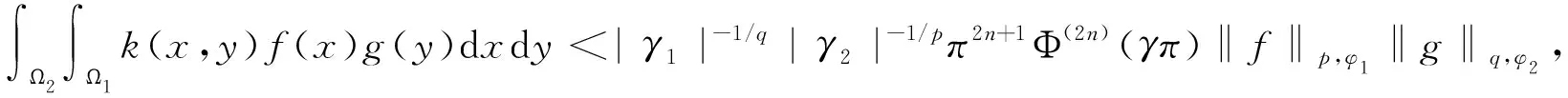
(14)

其中|γ1|-1/q|γ2|-1/pπ2n+1Φ(2n)(γπ)是满足式(14)的最佳常数因子.

证明由Hölder不等式，可得

{∫Ω2ϖ(y)[v(y)]q(1-γγ2)p[v′(y)]1-qgq(y)dy}1/q.

作代换uγ1(x)vγ2(y)=t，由引理2，可得

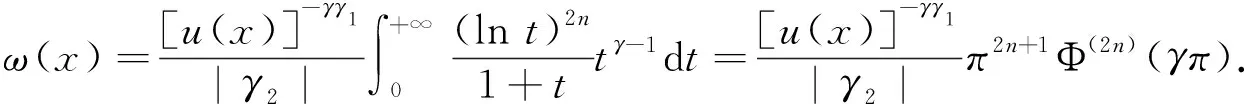
(16)

同理可算得

(17)

把式(16)和(17)代入到式(15)，可得

(18)

根据Hilbert不等式相关文献[2-3]常用的处理方法，不难证明式(18)不取等号，故式(14)成立.

最后只需证明式(14)中的常数因子最佳.事实上，若此常数因子不是最佳值，则有正数K满足

K<|γ1|-1/q|γ2|-1/pπ2n+1Φ(2n)(γπ),

(19)

使得式(14)中的常数因子改为K之后依旧成立，即

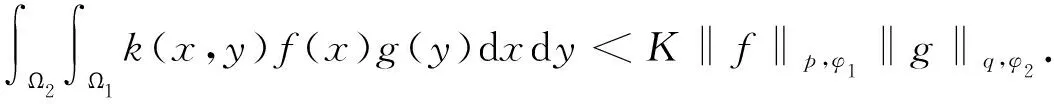
(20)

将引理3中定义的fm(x)和gm(y)分别替代式(20)中的f(x)和g(y)，利用引理3，则

令m→∞，则可得与式(19)矛盾的表达式，因此式(14)的常数因子是最佳的.定理1证毕.

在定理1中，令u(x)=x，v(y)=y，Ω1=Ω2=+，则有:

推论1设p>1，1/p+1/q=1，γ1,γ2∈，且γ1γ2≠0.另有0<γ<1，n∈，且Φ(x)=cscx.设f(x),g(y)≥0，φ1(x)=xp(1-γγ1)-1，φ2(y)=yq(1-γγ2)-1.且f(x)∈Lp,φ1(+)，g(y)∈Lq,φ2(+)，则

(21)

其中|γ1|-1/q|γ2|-1/pπ2n+1Φ(2n)(γπ)是满足式(21)的最佳常数因子.

在式(21)中，令γ1=β，γ2=-β，β>0，作代换G(y)=g(y)yβ，为形式统一美观，再把G(y)写成g(y)，则可得

(22)

其中φ1(x)=xp(1-γβ)-1，φ2(y)=yq(1-(1-γ)β)-1.在式(22)中，令n=0，则式(22)转化为

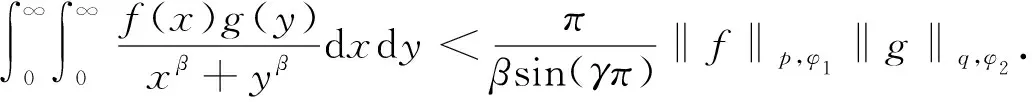
(23)

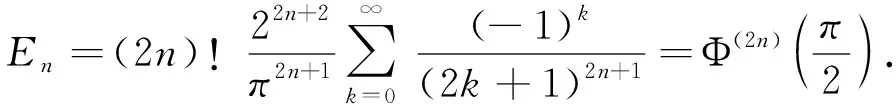
(24)

由此知式(22)可转化为式(3)，从而定理1是式(3)的推广.

在定理1中，令u(x)=ex，v(y)=ey，Ω1=Ω2=+，则有：

推论2设p>1，1/p+1/q=1，γ1,γ2∈，且γ1γ2≠0.另有0<γ<1，n∈，且Φ(x)=cscx.f(x),g(y)≥0，φ1(x)=x-pγγ1x，φ2(y)=e-qγγ2y，且f(x)∈Lp,φ1(+)，g(y)∈Lq,φ2(+)，则

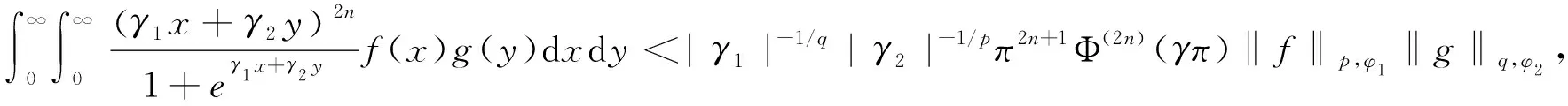
(25)

其中|γ1|-1/q|γ2|-1/pπ2n+1Φ(2n)(γπ)是满足式(25)的最佳常数因子.

在式(25)中，令γ1=β，γ2=-β，β>0，作代换G(y)=g(y)yβ，同样为了形式统一美观，把G(y)写成g(y)，则有

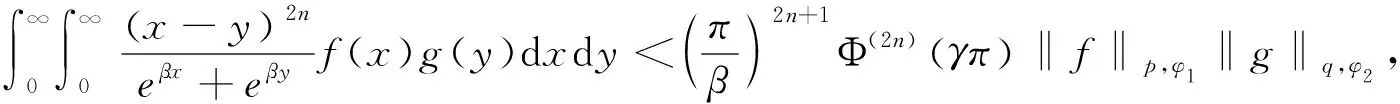
(26)

其中φ1(x)=x-pγβx，φ2(y)=eqγβy.