微分分次Frobenius代数

胡清秀，何济位

(杭州师范大学数学学院，浙江 杭州 311121)

1 预备知识

在研究非交换奇点解消理论中,需要考察分次Frobenius代数上的微分结构,再由Koszul对偶理论,将非交换奇点问题转化为研究微分分次模范畴的问题,为此本文引入了微分分次Frobenius代数的概念.文献[1]中给出了Frobenius代数的4个等价定义,在此基础上本文得到了微分分次Frobenius代数的另外3个等价定义,并研究了如何在三阶外代数上构造微分分次Frobenius代数.下面我们明确符号的约定以及一些预备知识.

定义1[1]令A为域K上的有限维代数.若存在一个映射σ∶A×A→K,对任意的x,y,z,x1,x2,y1,y2∈A,k∈K,满足以下条件:

1)σ(xy,z)=σ(x,yz);

2)σ(x1+x2,y)=σ(x1,y)+σ(x2,y);

3)σ(x,y1+y2)=σ(x,y1)+σ(x,y2);

4)σ(kx,y)=σ(x,ky)=kσ(x,y);

5)σ是非退化的,即仅当y=0时,对任意x都有σ(x,y)=0.

那么A就称作是一个Frobenius代数,σ称作A的Frobenius结构映射.满足条件1)～4)的映射称为结合的双线性映射.

定理1[1]若A是一个有限维代数,A*是A的对偶空间,则以下条件是等价的:

1)A是Frobenius代数;

2)A与A*作为左A-模是同构的;

3)A与A*作为右A-模是同构的;

4)A*作为左A-模或者右A-模是循环模.

定义2[2]设A=⊕i∈Ai是一个-分次代数.若存在一个次数为1的分次线性映射d∶A→A使得对任意齐次元a,b∈A满足:

1)d2=0;

2)d(ab)=d(a)b+(-1)|a|ad(b).

那么A就称作是一个微分分次代数,d称作是A的微分.

定义3[3]令A=⊕i∈Ai是一个微分为d的微分分次代数,设M=⊕i∈Mi是一个分次左A-模.若存在次数为1的线性映射d′∶M→M使得对任意m∈M,a∈A满足:

1)d′2=0;

2)d′(am)=d(a)m+(-1)|a|ad′(m).

那么M就称作是一个微分分次左A-模.

定义4[3]令A=⊕i∈Ai是一个微分为d的微分分次代数,设M=⊕i∈Mi为分次右A-模.若存在次数为1的线性映射d′∶M→M使得对任意m∈M,a∈A满足:

1)d′2=0;

2)d′(ma)=d(m)a+(-1)|m|ad′(a).

那么M就称作是一个微分分次右A-模.

2 微分分次Frobenius代数

令A=⊕i∈Ai是一个以d为微分的微分分次代数,则A*是一个微分分次左A-模,其左A-模结构以及微分由如下定义:

对任意的a,x∈A,f∈A*,令(af)(x)=(-1)|a|(|f|+|x|)f(xa),定义次数为1的线性映射d′∶A*→A*,对任意f∈A*[-n],x∈A,

d′(f)(x)=(-1)|f|+1f(d(x)).

(1)

可以验算:

d′2(f)(x)=(-1)|d′(f)|+1d′(f)(d(x))=

(-1)|f|(-1)|f|+1f(d2(x))=-f(0)=0,

即d2(f)=0.

且对任意x,a∈A,f∈A*[-n],

d′(af)(x)=(-1)|af|+1(af)(d(x))=

(-1)|a|+|f|+1(-1)|a|(|f|+|d(x)|)f(d(x)a)=

(-1)|a|(|f|+|x|)+|f|+1f(d(x)a);

(d(a)f)(x)=(-1)|d(a)|(|f|+|x|)f(xd(a))=(-1)(|a|+1)(|f|+|x|)f(xd(a));

(-1)|a|(ad′(f))(x)=(-1)|a|(-1)|a|(|f|+|x|+1)d′(f)(xa)=

(-1)|a|(|f|+|x|)(-1)|f|+1f(d(xa))=

(-1)|a|(|f|+|x|)+|f|+1f(d(x)a+(-1)|x|xd(a))=

(-1)|a|(|f|+|x|)+|f|+1f(d(x)a)+(-1)|a|(|f|+|x|)+|f|+|x|+1f(xd(a))=

(-1)|a|(|f|+|x|)+|f|+1f(d(x)a)+(-1)(|a|+1)(|f|+|x|)+1f(xd(a)).

即d′(af)=d(a)f+(-1)|a|ad′(f).从而A*是一个微分分次左A-模.

同理可以验算A*是一个微分分次右A-模,其微分同等式(1),右A模结构为对任意a,x∈A,f∈A*, (fa)(x)=f(ax).

定义6令A=⊕i∈Ai是一个有限维微分分次代数,若存在一个结合的分次非退化双线性型σ∶A×A→K使得对任意齐次元a,b,c∈A都有

σ(d(a),b)=(-1)|a|+1σ(a,d(b))，

(2)

其中d为A的微分,则称A是一个微分分次Frobenius代数.

本文主要考虑正分次的微分分次Frobenius代数,即A=⊕i∈Ai,对于i<0,Ai=0.

定理2若A是一个有限维正分次的微分分次代数,则以下命题等价:

1)A是微分分次Frobenius代数;

2)存在n∈,A与A*[-n]作为微分分次左A-模是同构的;

3)存在n∈,A与A*[-n]作为微分分次右A-模是同构的;

4)存在n∈,f∈A*,使得Af=A*[-n]且d′(f)=0.

证明1)⟹2).A=A0⊕A1⊕…⊕An,则A*=Hom(An,K)⊕Hom(An-1,K)⊕…⊕Hom(A0,K).记B=A*[-n],则作为向量空间Bi=Hom(An-i,K),i∈.定义映射

(3)

这里,对任意齐次元a,x∈A,

σ(-,a)(x)=(-1)|a||x|σ(x,a)=(-1)|a||x|σ(xa,1).

由1∈A0,那么仅当|x|+|a|=n时,σ(-,a)(x)有可能不为0.若a∈Ai,当|x|≠n-i时,σ(-,a)(x)=0,也就是说:σ(-,a)∈Hom(An-i,K)=Bi,即φ是保持次数的.

再证φ是左A-模同构映射.对任意齐次元a,b,x∈A,

(aφ(b))(x)=(-1)|a|(|φ(b)|+|x|)φ(b)(xa)=(-1)|a|(|b|+|x|)σ(-,b)(xa)=

(-1)|a|(|b|+|x|)(-1)|b|(|x|+|a|)σ(xa,b)=(-1)(|a|+|b|)|x|σ(x,ab)=

σ(-,ab)(x)=φ(ab)(x).

从而φ是A与B的左A-模同态.若对∀b∈A,都有σ(-,a)(b)=(-1)|a||b|σ(b,a)=0,则由σ是非退化的,得a=0,即仅当a=0时φ(a)=0,所以φ是单射.又dim(A)=dim(A*),从而φ是双射,因此A与A*[-n]作为左A-模是同构的.

最后证明φ与微分是交换的.记f=σ(-,1),则|f|=0.对任意a∈A,

φ(a)=φ(a·1)=aφ(1)=af,

那么就有

φ(d(a))=d(a)f;

d′(φ(a))=d′(af)=d(a)f+(-1)|a|ad′(f).

而对任意x∈A,

(ad′(f))(x)=(-1)|a|(|d′(f)|+|x|)d′(f)(xa)=

(-1)|a|(|d′(f)|+|x|)(-1)|f|+1f(d(xa))=

(-1)|x|f(d(x)a+(-1)|x|xd(a))=

(-1)|x|(σ(-,1)(d(x)a)+(-1)|x|σ(-,1)(xd(a)))=

(-1)|x|(σ(d(x)a,1)+(-1)|x|σ(xd(a),1))=

(-1)|x|(σ(d(x),a)+(-1)|x|σ(x,d(a)))=0.

从而φd=d′φ,所以A与A*[-n]作为微分分次左A-模是同构的.

1)⟹3).类似于1)⟹2).

2)⟹4).假设A与A*[-n]作为左A-模同构的映射为φ,则对任意a∈A,

φ(a)=φ(a·1)=aφ(1),

从而A*[-n]=φ(A)=Aφ(1).令f=φ(1),则A*[-n]=Af.由φd=d′φ,对任意a∈A,

φ(d(a))=d′(φ(a)),

d(a)f=d′(af),

d(a)f=d(a)f+(-1)|a|ad′(f).

再由a的任意性,d′(f)=0.

同理可证3)⟹4).

4)⟹1).假设存在f∈A*[-n]使得Af=A*[-n]且d′(f)=0.对任意a,b∈A定义双线性映射σ∶A×A→K,σ(a,b)=f(ab),则对任意a,b,c∈A,

σ(ab,c)=f((ab)c)=f(a(bc))=σ(a,bc).

若对∀a∈A,都有σ(a,b)=f(ab)=0,则b=0,从而σ是非退化的.

对∀a,b∈A,由d′(f)=0有

d′(f)(ab)=0,

(-1)|f|+1f(d(ab))=0,

f(d(a)b+(-1)|a|ad(b))=0,

f(d(a)b)=(-1)|a|+1f(ad(b)),

σ(d(a),b)=(-1)|a|+1σ(a,d(b)).

定理得证.

3 三阶外代数上的微分分次Frobenius结构

本节主要讨论三阶外代数上的所有可能的微分分次Frobenius代数结构,并作出同构分类.首先我们不难验证下面这个引理.

引理1令A=K⊕A1⊕A2⊕…⊕An是由A1生成的微分分次代数,d是A的微分.设x1,x2,…,xj∈A1,则

(4)

现在考虑三阶外代数,研究其构成微分分次Frobenius代数的条件.

定理3令V是以{x,y,z}为一组基的三维线性空间,∧(V)为V生成的外代数,定义d∶V→V∧V如下:

则d定义了∧(V)上的微分当且仅当

(5)

A0=K;A1=span{x,y,z};

A2=span{y∧z,z∧x,x∧y};A3=span{x∧y∧z}.

考虑A2中元素:

d(y∧z)=d(y)∧z+(-1)|y|y∧d(z)=d(y)∧z-y∧d(z)=

(k4y∧z+k5z∧y+k6x∧y)∧z-y∧(k7y∧z+k8z∧x+k9x∧y)=

k6x∧y∧z-k8y∧z∧x=(k6-k8)x∧y∧z;

d(z∧y)=d(z)∧y+(-1)|z|z∧d(y)=d(z)∧y-z∧d(y)=

(k7y∧z+k8z∧x+k9x∧y)∧y-z∧(k4y∧z+k5z∧y+k6x∧y)=

k8z∧x∧y-k6z∧x∧y=(k8-k6)x∧y∧z.

因此d(y∧z)=-d(z∧y).

同理可证:

d(z∧x)=-d(x∧z)=(k1-k3)x∧y∧z;

d(x∧y)=-d(y∧x)=(k2-k4)x∧y∧z.

而由于d(A3)∈A4,那么必然有d(A3)=0.这样d(ab)=d(a)b+(-1)|a|ad(b)对任意a,b∈A都成立.

接下来考虑如何使得d2=0.由于d(A0)=0,d(A3)=0,d2(A2)∈A4,故只需再令d2(A1)=0 即可.

d(d(x))=d(k1y∧z+k2z∧x+k3x∧z)=

k1d(y∧z)+k2d(z∧x)+k3d(x∧z)=

k1(k6-k8)x∧y∧z+k2(k1-k3)x∧y∧z+k3(k2-k4)x∧y∧z=

(k1k6+k1k8+k1k2+k3k4)x∧y∧z.

同理可证:

d(d(y))=(k4k8-k5k7+k3k5-k2k6)x∧y∧z;

d(d(z))=(k6k7-k3k8+k2k9-k4k9)x∧y∧z.

即d2(A1)=0,当且仅当

从而定理得证.

更进一步地,在上述的微分分次代数A上构造如下双线性映射σ,对任意齐次元a,b∈A,

(6)

容易验证σ是一个结合的非退化双线性型.

定理4保留上述符号,A是以d为微分、σ为Frobenius结构映射的微分分次Frobenius代数的充要条件是D为对称矩阵.

证明必要性:若A是以d为微分、σ为Frobenius结构映射的微分分次Frobenius代数,那么对任意齐次元a,b∈A都有σ(d(a),b)=(-1)|a|+1σ(a,d(b)).即

σ(d(a),b)+(-1)|a|σ(a,d(b))=0,

σ(d(a)∧b,1)+σ((-1)|a|ad(b),1)=0,

σ(d(a)∧b+(-1)|a|ad(b),1)=0,

σ(d(a∧b),1)=0.

由于σ是Frobenius结构映射,可得d(A2)=0,即

从而

D为对称矩阵.

充分性:若D是对称矩阵,容易验证A是以d为微分、σ为Frobenius结构映射的微分分次Frobenius代数.

□

引理2设V为三维向量空间, {x,y,z}和{a,b,c}是V的两组基,若(∧(V),d)为微分分次Frobenius代数,且

则存在可逆矩阵M使D1=MD2MT.

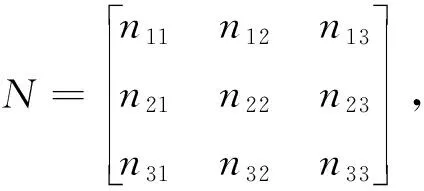
其中,Nij(i,j∈{1,2,3})是nij的余子式,N*是N的伴随矩阵,(N*)T是N*的转置.那么就有

从而

□

定理5设V是复数域上三维向量空间,若(∧(V),d)为微分分次Frobenius 代数,则在适当选择V的基的情况下,微分d必为以下4种情况之一:

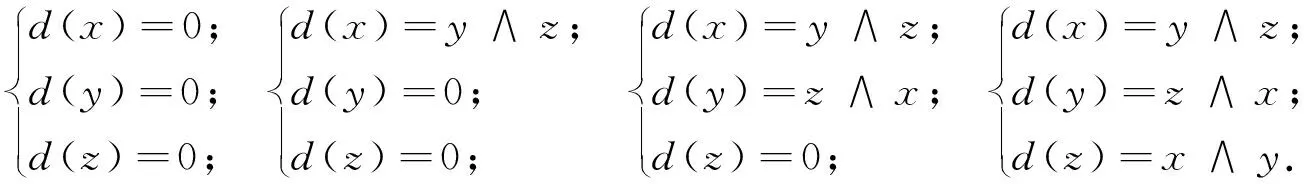
(7)

令

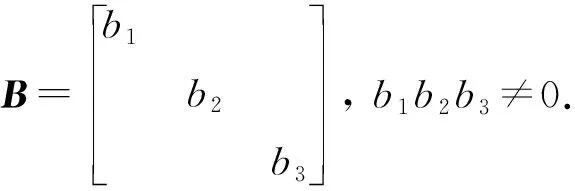
同理可证当秩(A)=0,1,2时,A分别合同于D0,D1,D2.由引理2,对于任意三阶微分分次Frobenius代数,可以选取适当的基使得其对应的微分作用的矩阵为对角矩阵.

□