基于分解的高维多目标改进进化算法

乔钢柱，王瑞，孙超利*

（1.太原科技大学计算机科学与技术学院，太原 030024；2.中北大学大数据学院，太原 030051）

0 引言

自然科学、社会科学和工程技术等许多领域中都存在同时优化多个目标的问题，例如流水车间调度［1］和电力系统规划［2］，其优化目标之间往往是相互冲突的，这些优化问题统称为多目标优化问题。由于其多个目标之间的相互冲突，所能找到的往往是一组解集，而不是能同时使得所有目标取得最优的一个解。

多目标优化问题的数学模型如下：

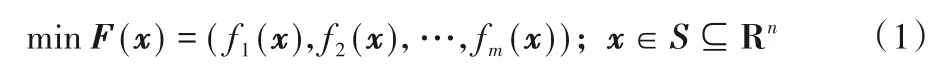
式中：x=(x1，x2，…，xn)为n维决策变量，S为x的可行域；fi（x）表示x的第i(i=1，2，…，m)个目标函数，m为目标函数个数。通常当优化目标个数超过3 个时，称之为高维多目标优化问题（Many-objective Optimization Problems，MaOPs）［3］。

进化多目标算法［4-5］由于其具有较好的全局搜索能力，且能够同时提供多个候选解，从而被越来越多地用于求解多目标优化问题。到目前为止，学者们针对多目标优化问题已提出了很多进化优化算法，如快速排序算法II（Non-dominated Sorting Genetic Algorithm II，NSGA-II）［4］、基于分解的多目标进化算法（MultiObjective Evolutionary Algorithm based on Decomposition，MOEA/D）［6］，以及基于指标的进化算法（Indicator-Based Evolutionary Algorithm，IBEA）［7］。然而，随着优化目标函数个数的增加，互不支配的个体数量急剧增加，导致传统的基于Pareto 支配关系的选择策略失效，很难找到新的Pareto 占优关系；同时，目标空间维度的增大增加了获得均匀分布解的难度。为此，学者们提出了不同的求解高维多目标问题的优化算法以期获得较好的最优解集。

一般来说，求解高维多目标优化问题的算法大致可分为四类：

1）第一类是基于Pareto 支配关系的高维多目标优化方法。如：Zhang 等［8］提出了基于拐点的进化算法（Knee pointdriven Evolutionary Algorithm，KnEA），利用拐点选择策略替代NSGA-II 中基于拥挤度的选择策略。Li 等［9］利用偏移密度估计（Shift-based Density Estimation，SDE）机制改变解在空间中的位置，使得支配关系发生变化，从而加速收敛。Qasim等［10］提出了基于排序支配的对抗差分进化算法（Rankingdominance-based algorithm with Opposition-based Differential Evolution，RODE）算法，在该算法中采用AR（Average Rank）方法选择个体。肖婧等［11］提出了一种基于全局排序的高维多目标优化（Global Ranking based Many-Objective Differential Evolution，GR-MODE）算法，首先采用全局排序提高选择压力，然后采用Harmonic 平均拥挤距离对个体进行全局密度估计，提高现有局部密度估计方法的精确性。谭阳等［12］提出了一种以超球型支配关系降低种群中非支配解数量的粒子群优化（Particle Swarm Optimization，PSO）算法，该算法采用模糊支配策略维持选择压力，另外通过全局极值的选择和外部档案的维护保持种群个体在目标空间的分布。然而，随着目标数量的增多，大部分个体之间都为互不支配关系，导致选择压力降低，因此增加了这类算法在寻找高维多目标非支配最优解集的困难。

2）第二类是基于分解的高维多目标优化方法。Zhang等［6］提出的MOEA/D 将多目标优化问题通过参考向量转换成若干个单目标优化问题，并对其同时进行优化。然后，学者们基于MOEA/D 提出了很多求解高维多目标优化问题的改进算法，如基于分解、自适应繁殖选择机制辅助的多目标进化算法（MultiObjective Evolutionary Algorithm based on Decomposition with an Adaptive Mating Selection mechanism，MOEA/DAMS）［13］和将一个多目标分解成多个简单多目标子问题进行求解的多目标进化算法（Multiobjective Optimization Evolutionary Algorithm based on Decomposition of a Multiobjective optimization problem into a number of simple Multiobjective subproblems，MOEA/D-M2M）［14］。He 等［15］提出了一种基于动态分解排序（Dynamical-Decomposition-based Ranking，DDR）方法的进化高维多目标优化算法，该算法提出动态分解策略，将解本身作为参考向量，另外子空间的划分由种群的解和原来的子空间决定。Cheng 等［16］提出了参考向量引导的进化算法（Reference Vector guided Evolutionary Algorithm，RVEA），基于角度和到理想点的距离提出了一种新的环境选择策略。Qin 等［17］提出了基于分解框架的改进粒子群优化（Modified Particle Swarm Optimization based on Decomposition with Different ideal points，MPSO/DD）算法，利用多个理想点引导个体，一方面保证了种群的均匀性，另一方面能够加速引导个体的收敛。巩敦卫等［18］提出了一种基于目标分解的高维多目标并行进化优化方法，通过目标函数分组与聚合，将一个高维多目标优化问题分解为若干子问题，从而降低了问题求解的难度。在基于分解的这类算法中，如何选择参考向量以及如何基于参考向量进行环境选择是找到好的Pareto非支配最优解集的难点。

3）第三类是基于指标的高维多目标优化方法。IBEA 是第一个基于指标的多目标进化算法。虽然它在高维多目标问题收敛方面表现良好，但由于其指标缺乏多样性维护，它的多样性很差。While 等［19］提出的基于超体积（HyperVolume，HV）的进化算法利用蒙特卡罗模拟近似精确超体积值，超体积是评估收敛性和多样性的度量。基于反世代距离（Inverted Generation Distance，IGD）的多目标进化算法（IGD indicatorbased Multi-Objective Evolutionary Algorithm，MOEA-IGD）［20］是将反世代距离指标作为个体适应值的评价标准，它被认为是一种可靠的性能指标，可以量化多目标进化算法的收敛性和多样性。Liu 等［21］提出了一种基于一个接一个选择策略的进化算法（Evolutionary Algorithm using a one-by-one selection strategy，1by1EA），该算法根据一个收敛指标和一个分布指标选择个体，前者测量解与帕累托最优前沿之间的距离，后者测量其彼此之间的距离。基于指标的方法能够生成符合期望性能的结果，但是算法的计算成本较高，很难达到快速验证的结果。

4）最后一类是不能完全归到以上某一类的高维多目标优化算法。例如，Li等［22］将基于分解和基于占优的方法结合，充分利用两种方法的优势，权衡算法的收敛性和多样性，提出了基于支配和分解的进化高维多目标优化算法（highdimensional Many-Objective optimization Evolutionary Algorithm based on Dominance and Decomposition，MOEA/DD）。Deb等［23］结合NSGA⁃II 的支配关系以及分解方法中参考点的使用方法，提出了NSGA⁃III 算法。Li 等［24］提出了收敛性指标和多样性指标，基于该两种指标进行非支配排序实现环境选择，将在高维多目标空间的搜索转换为在两个目标空间的搜索，提高了高维多目标优化的非支配解集的搜索能力。朱占磊等［25］基于线性权重聚合函数和支配关系提出了一种线性权重最优支配关系，将此支配关系代替Pareto支配关系。

基于参考向量的进化算法RVEA 是Cheng 等［16］提出的用于求解高维多目标优化问题的方法，该方法不仅提供了自适应的参考向量产生方法，同时提出了基于角度和到理想点距离的新的环境选择标准，称为角度惩罚距离（Angle⁃Penalized Distance，APD），在进化过程中综合考虑了收敛性和分布性，以期能够获得稳定的具有较好收敛性能的高维多目标进化算法。然而，由于RVEA 采用随机选择父代，导致在高维目标空间距离远的父代差异性大，可能无法生成优秀的子代。另外，仅考虑关联个体的子空间，减小了种群的搜索区域，不能很好地保证种群的多样性。因此，本文基于RVEA 框架提出了一种基于分解的高维多目标改进进化算法（Improved highdimensional Many-Objective Evolutionary Algorithm based on Decomposition，IMaOEA/D）。在IMaOEA/D 中，针对分配不同数量个体的子空间，引入精英父代选择策略，该策略利用个体在目标空间距离理想点的距离d1来选择父代，以期产生较好后代来加快算法的收敛。在环境选择中，RVEA 不考虑未分配个体的子空间，导致种群的多样性变差，故为了保持多样性，本文首先基于角度惩罚距离（APD）值选择下一代，随后对于未分配个体的子空间采用角度指标选择距离该参考向量近的个体作为下一代中个体。实验结果表明，本文算法在求解高维多目标优化问题，特别是针对退化优化问题上能够获得较好的优化性能。

1 RVEA

基于参考向量的进化算法RVEA 的主要实现步骤和普通的基于分解的多目标优化算法一致。在RVEA 中，主要是提出了一种自适应的参考向量设定方法，同时基于参考向量提出了一种角度惩罚距离指标，用于多目标优化中的环境选择。

1.1 角度惩罚距离

RVEA 提出使用角度惩罚距离值进行环境选择，其既考虑了个体的收敛性，同时也根据个体目标函数值和其相关参考向量之间的夹角考虑种群的多样性，其计算式如下：

式中：M表示目标的数目；t和tmax分别为种群当代进化的代数和种群进化的最大代数；α是一个预先设置的可变参数，可以控制P(θt，i，j)的变化率；γvt，j是当代种群中参考向量vt，j与其他向量之间角度最小值。γvt，j计算式如下：

其中N是参考向量的数目。

1.2 自适应参考向量

通常情况下，参考向量是在目标空间均匀产生的。然而，在各类优化问题中，由于最优解集在目标空间中并不一定能够均匀划分，因此均匀产生的参考向量可能会阻碍最优解集的获得。为此，在RVEA 中，Cheng 等［16］提出了一种自适应的参考向量产生方法，其更新方式如下：

2 基于分解的高维多目标改进进化算法

在进化算法中，子代产生的位置会影响算法的寻优速度，而在基于参考向量的进化算法RVEA 中，子代是通过随机选择两个父代得到的，随着目标个数的增加，个体在目标空间的分布更加稀疏，随机选择父代不利于算法的收敛性。另外，在RVEA 中，其每个参考向量不一定能够分配上个体，因此随着迭代的增加，算法不一定能够很好地保持种群多样性。为此，针对这两个问题，本文提出了一种基于分解的高维多目标改进优化算法（IMaOEA/D）。IMaOEA/D 的伪代码如算法1所示。

算法1 IMaOEA/D。

从算法1 中可以看到，同其他基于分解的求解高维多目标优化问题的进化算法一样，IMaOEA/D首先均匀产生若干单位参考向量，并产生一个规模为N的种群。当评价次数未达到最大评价次数时，通过对每个个体根据本文提出的算法来选择父代个体（具体见2.1节中算法2），对其交叉变异产生新个体。随后，对当前父子代基于本文提出的环境选择策略（具体见2.2 节中算法3）实现下一个父代的选择。算法中，子代的产生采用广泛使用的二进制交叉（Simulated Binary Crossover，SBX）［26］和多项式变异（Polynomial Mutation）［27］。

2.1 父代选择

选择什么样的父代来产生下一代对于算法的最优解集搜索具有重要的影响。在本文中，主要考虑通过父代选择来加快子空间的搜索。故在IMaOEA/D 中，根据参考向量来寻找父代并产生子代。对任何一个参考向量，从分配给该参考向量的个体集中，根据沿该参考方向到理想点的距离d1的大小选择两个父代个体。d1的计算方法如下：

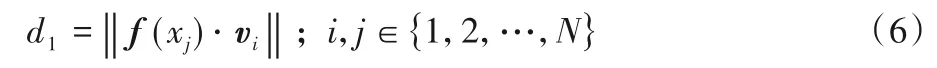
其中：f(xj)为个体xj的目标函数向量值；vi代表的是第i个参考向量。需要注意的并不是所有参考向量都有分配个体，故对于未能分配至少2 个个体的参考向量，选择距离理想点最近的一个或者两个个体作为子代的父代个体。算法2 给出了具体的选择方法。

算法2 父代个体的选择方法。

2.2 环境选择

在本文方法中，仍旧使用RVEA 中提出的角度惩罚距离指标来进行环境选择。然而，并不是所有的参考向量都一定能有个体和其关联，有可能导致下一父代的种群多样性缺失。为此，在IMaOEA/D 中，对于没有个体和其关联的参考向量，寻找在当前种群中和其夹角最小的个体，并将其分配给该参考向量，从而保证每个参考向量至少有一个个体是和其相关联的。算法3 给出了本文方法中的环境选择策略。从算法3中可以看到，对于任意一个参考向量vi，若分配给其的个体数至少1个，则选择APD值最小的个体和该参考向量关联（第5）行）；否则选择父子代种群个体中和该参考向量夹角最小的个体和该参考向量关联（第7）行）。

算法3 环境选择。

3 实验与结果分析

3.1 实验设置

为验证本文算法的有效性，在具有10个目标和15个目标的MaF［28］问题上进行了测试。所有实验均在处理器是Intel Core i7-2670QM CPU @2.2.0 GHz 2.19 GHz、内存为8 GB 的PC 上通过Matlab 2016 实现。以下为实验的一些基本设置：1）算法在每个测试问题独立运行20 次；2）最大代数为1000；3）种群大小和参考向量数量一样，10个和15个目标的种群大小分别设为275和135；4）本文算法及其对比算法均采用传统的二进制交叉和多项式变异操作，交叉和变异概率分别为1和1/D，D是决策变量的维度，交叉和变异的分布指标都是20。

在角度惩罚距离公式中，参数α控制惩罚函数P（θ）的变化率，参数fr控制参考向量更新的次数。为了验证这两个参数对本文算法的影响，先固定一个参数，然后对另一个参数进行分析。固定参数fr为0.5，α的取值范围为［1，9］的9 个整数，其值越大表示收敛性越在前期占主导地位。分别在10、15 个目标的MaF8 和MaF10 上作了测试，其中MaF8 的目标为线性、退化问题，MaF10 的目标为混合、偏置问题。图1 给出了不同参数α在这两个测试问题上的IGD 变化。为了验证参数fr对算法的影响，固定α=2，然后使fr在［0.1，0.5］取值。在MaF8 和MaF10 问题进行实验，独立运行20 次，统计结果如图2所示。

图1 不同α值下不同测试问题的IGD平均值Fig.1 IGD mean values of different test problems with different α values

图2 不同fr值下不同测试问题的IGD平均值Fig.2 IGD mean values of different test problems with different frvalues

从图1 中可以看到，给定fr值时，不同的α值对于不同的测试问题，其IGD 值的变化相对平稳，表明算法性能对α不是很敏感。但是高维空间中相对较小的α值使收敛性和分布性的重要程度在进化前后期的分配更为合理。因此，本文取α=2。

从图2 中可以看到，在两个测试问题中，随着fr值不断增大，IGD值变化平稳。对于线性、退化的15目标的MaF8问题，其IGD值随着fr值的增大而减小。对于解决如MaF8和MaF10等真实Pareto 面复杂的问题，太频繁地更新参考向量不利于算法的稳定性。本文取更新参考向量的参数fr=0.5。

3.2 结果分析

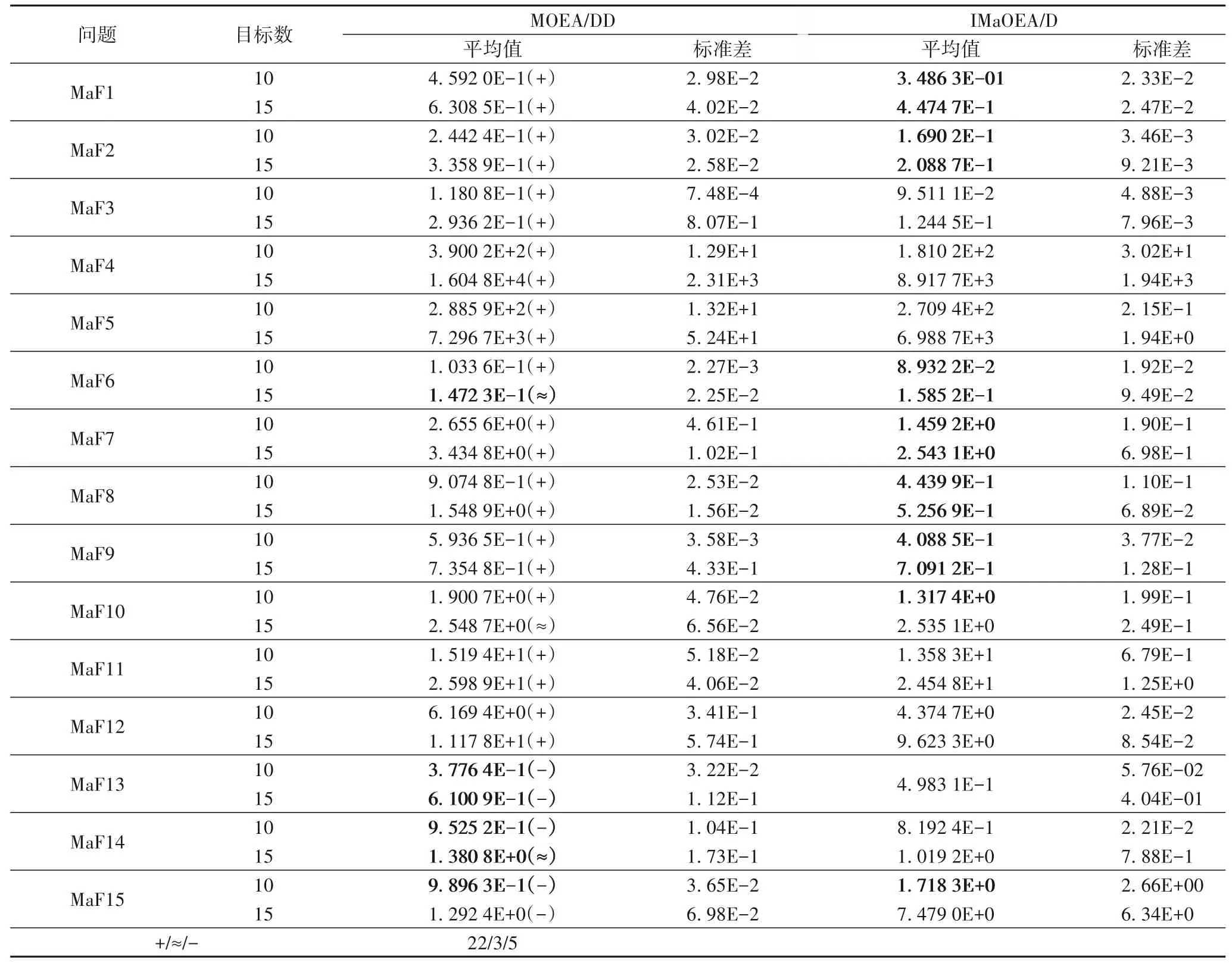
将本文方法在高维目标函数测试集MaF 上进行了测试，并和其他近年来发表的基于分解的、具有较好代表性的4 个算法进行了对比，包括参考向量引导的进化算法（RVEA）［16］、基于参考方向的Pareto 增强进化算法（Strength Pareto Evolutionary Algorithm based on Reference direction，SPEA/R）［29］、基于参考点支配的非支配排序遗传算法II（Reference Point-based Dominance in Nondominated Sorting Genetic Algorithm-II，RPDNSGA-II）［30］，以及基于支配和分解的进化高维多目标优化算法（MOEA/DD）［22］。为了公平比较，所有算法的种群规模和运行代数均保持一致，对比算法的其他参数设置选择各自文献中给出的推荐参数值。所有算法的IGD 指标值均为独立运行20 次后的平均值，表1 是所有算法独立运行20 次获得的IGD 平均值与标准差，其中最好的结果用加粗表示。

另外，为了比较本文所提算法与另外4 种算法获得的平均IGD 值之间差异的显著性，本文采用Wilcoxon 秩和检验进行两两比较，显著性水平取0.05，表中“+”“-”“≈”分别表示IMaOEA/D 显著优于、显著劣于和无差别于其他算法。从表1的数据可以看出，算法IMaOEA/D 整体的性能优于其他对比算法。从秩和检验结果分析，在30 个MaF 测试问题上，算法IMaOEA/D 在其中的14 个上显著优于RVEA，18 个上显著优于SPEA/R，16 个上显著优于RPDNSGA-II，以及在22 个上显著优于MOEA/DD。尤其在测试问题MaF6、MaF8 和MaF9 上，本文算法IMaOEA/D 取得了明显的优势，表明该算法能较好地处理退化问题。

表1 不同算法在不同目标维数的MaF测试问题上获得的IGD平均值与标准差Tab.1 IGD mean values and standard deviations obtained by different algorithms on MaF test problems with different dimensions of objectives

续表

4 结语

本文提出了一种基于分解的高维多目标改进优化算法（IMaOEA/D），通过引入父代选择机制加快收敛，通过在环境选择中确保每个参考向量都有一个个体和其对应来提高种群的多样性，从而平衡算法的收敛能力和种群多样性。在具有10个和15个目标的MaF优化问题上进行了测试，并将本文算法和其他4 个基于分解的优化算法进行了对比。实验结果表明，本文算法在大部分高维多目标MaF 优化问题上具有较好的寻优能力，且在退化问题上具有一定的寻优优势。然而，从实验结果可以看出，本文算法在Pareto 面为凸面的问题，如MaF3、MaF5 和MaF15 等问题上，其性能表现较差。因此，今后我们将针对这类问题做进一步的研究，以期能够获得这类问题的较优非支配解集。