基于多种群组合策略的人工蜂群算法

李文霞，刘林忠，代存杰，李玉

（兰州交通大学交通运输学院，兰州 730070）

0 引言

近年来，随着群智能优化算法的高效发展，其在解决复杂优化问题时体现出良好的求解性能，受到学者们的广泛关注，群智能优化算法源于对自然界中生物群体行为的模拟，主要包括遗传算法［1］、蚁群算法［2］、粒子群算法［3］、人工蜂群（Artificial Bee Colony，ABC）算法［4］等。遗传算法对自然界中生物的自然淘汰进化过程进行模拟，主要通过交叉、变异、选择算子来实现，该算法的改进方向包括自适应算子的引入［5］、多种群方式的改进［6］、编码技术的改进［7］及混沌理论的加入［8］等角度；蚁群算法模拟蚂蚁觅食行为，通过信息素的正反馈机制寻找自蚁巢到食物源的最短路径，近年来蚁群算法的改进主要集中在信息素的更新策略［9］及路径选择策略［10］两个方面；粒子群算法对生物界鸟类觅食行为进行模拟，通过对全局极值的对比，及时调整粒子的搜索速度与方向，相关学者从粒子群多样性的控制［11］、算法中参数的改进［12］、初始化过程中粒子拓扑结构的优化［13］等方面出发对算法进行改进。上述群体智能算法的优化改进逐渐趋于成熟，一些新型群体智能算法的提出受到了国内外学者的广泛关注。

受蜜蜂群体觅食行为启发，Karaboga［4］于2005 年提出了人工蜂群（ABC）算法。相较于其他群体智能算法，人工蜂群算法中的劳动分工和协作机制有效提高了算法的全局搜索能力，同时正反馈的寻优策略加快了全局寻优过程，求解效率更高，并且在求解连续优化问题和组合优化问题时均表现出优越的性能，具有广泛的适用性，已在神经网络训练［14］、系统工程设计［15］、聚类分析［16］和图像信号处理［17］等众多领域得到了广泛应用。

ABC 性能主要取决于搜索方程和个体选择策略，基本ABC 的搜索方程包含随机个体信息较强，相较于一般群体智能优化算法，表现出良好的全局搜索优势，但同时存在收敛速度慢、求解精度低、易陷入局部最优等问题。算法的全局搜索和局部开发在求解过程中表现出互补性，但在操作上又具有矛盾性，为更好地平衡二者，同时满足求解效率和求解精度要求，相关学者从搜索机制改进和融合算法等方面进行了有效研究。向万里等［18］将最优个体指导信息引入雇佣蜂阶段，利用个体信息对跟随蜂的扰动，进一步平衡探索能力和开发能力。Kiran等［19］考虑算法的下降梯度，对较强地位的维度进行搜索，以提高算法的搜索深度。孟红云等［20］利用精英信息、随机信息及邻域信息指导雇佣蜂阶段搜索，同时在观察蜂阶段提出全局精英信息和当代最优信息指导搜索，使算法的寻优能力得到显著提高。Jadon 等［21］受差分进化（Differential Evolution，DE）思想的启发，提出具有差异进化的混合人工蜂群（Hybrid Artificial Bee Colony with Differential Evolution，HABCDE）算法，将DE 和ABC 融合，以提供良好的搜索平台，在提高搜索的深度的同时不影响探索的广度。魏锋涛等［22］为提高种群多样性，构建了混沌反向解初始化机制，并构建跟随蜂量子更新搜索策略，进一步地提高蜜源邻域内的寻优质量。

上述算法改进在不同程度上提高了ABC 的寻优能力，但仍有较大改进空间，如何进一步提高算法的应用范围、收敛速度及收敛精度，仍需深入研究，因此本文提出了一种基于多种群组合策略的人工蜂群（Artificial Bee Colony based on Multipopulation Combination strategy，MCABC）算法。为提高算法搜索效率，针对雇佣蜂和跟随蜂分别设计不同的组合策略，在跟随蜂阶段划分了自由种群和非自由种群，针对不同属性的个体采用对应的子策略；同时在搜索方程中改进了维度信息更新机制，进一步提高了算法在高维复杂函数的求解性能。为验证本文提出算法的有效性，采用15 个标准测试函数，将MCABC与多个具有代表性的改进ABC算法进行对比，进一步验证了算法的寻优性能。

1 标准人工蜂群算法

人工蜂群算法思想来源于仿生学中蜜蜂群体觅食行为，蜂群个体分为雇佣蜂、跟随蜂和侦查蜂3 种类型，雇佣蜂和跟随蜂数量各占蜂群总数一半，侦查蜂数量与雇佣蜂相同，雇佣蜂负责勘察并将蜜源信息分享给跟随蜂，跟随蜂依据蜜源质量通过轮盘赌方式选择，并在附近寻找更好的蜜源，当某一蜜源被舍弃时，雇佣蜂转化为侦查蜂寻找新蜜源，三种蜂群发挥各自效用，准确有效完成蜜源的搜索和采集任务。

1.1 初始化

在标准ABC 中，当前解空间通过式（1）初始化种群，一个蜜源位置代表问题的一个可行解，蜜源的位置用D维向量表示Xi=[xi1，xi2，…，xiD]，其中：

其中：i=1，2，…，SN，SN是解（蜜源）的数量，j=1，2，…，D，D是解的维数；xi，j是第i个解的第j维；ϕi，j是［0，1］的随机数；、是j维的上、下界。

1.2 雇佣蜂

雇佣蜂通过式（2）在初始解附近搜索新解，进行局部搜索，并对每个蜜源的适应度进行计算，进而评价食物源的优劣，若新解优于初始解，则保留新解，迭代重复值Counter（i）加1；否则保留初始解，迭代重复值Counter（i）不变，即通过贪婪选择更新解同时记录蜜源开采情况。

其中：vi，j是更新后的解；xk，j是在种群中随机选择与xi，j不相同的解；φi，j是［-1，1］的均匀随机数。

1.3 跟随蜂

跟随蜂依据雇佣蜂传递的蜜源信息，通过式（3）轮盘赌概率选择某一蜜源，蜜源的适应度值越高，可行解的质量越好，被选择的概率越大。随后跟随蜂采用式（2）进行邻域搜索，并采用贪婪选择更新解，在保留优势个体的同时兼顾蜜源的探索能力。

其中：pi是解i的选择概率；fiti是解i的适应度值。

其中：fi是目标函数值。

1.4 侦查蜂

当某一蜜源长期未更新时，当前蜜源将被遗弃，雇佣蜂转变为侦查蜂，通过式（1）随机产生新蜜源，算法进入雇佣蜂阶段。侦查蜂的操作有效避免了算法过早陷入局部最优，提高了算法的全局探索能力。

2 基于多种群组合策略的人工蜂群算法

2.1 研究思路

标准ABC 受制于搜索策略的单一和搜索方程的信息匮乏，算法的搜索导向性和多源信息的融合性较弱，表现为一种随机的无向搜索，这种无向搜索虽然一定程度上增强了全局探索能力，但同时也降低了收敛速度和求解精度，且迭代过程中只更新D维中随机选择的一个维度，使其在求解高维函数时寻优能力下降。鉴于此，本文针对雇佣蜂和跟随蜂分别设计组合策略CS1和CS2。在雇佣蜂阶段采用CS1策略，以提高初始种群的深度与广度；在跟随蜂阶段，为进一步明确跟随蜂个体的任务重点，针对自由子集和非自由子集，采用CS2 策略，其中，自由个体增强探索能力，非自由个体侧重开发能力；最后，在搜索方程中融入异维单点更新和多维匹配更新机制，以提高算法在高维问题中的优化效率。

2.2 维度更新机制

ABC中固有的同维单点更新机制能够有效胜任低维问题的求解，而这种单一的更新模式在面对高维问题时求解效率显著下降，既有研究证明，异维搜索避免了ABC 单一搜索模式的局限性，增强了算法的全局搜索能力，有利于算法摆脱局部最优［23-24］。为此，本文将多维匹配更新机制和异维单点更新机制引入搜索方程，有效利用多维信息的并行优化和异维信息的协同交互，提高算法在求解高维问题时的精度。多维匹配更新示意如图1所示，异维单点更新示意如图2所示。

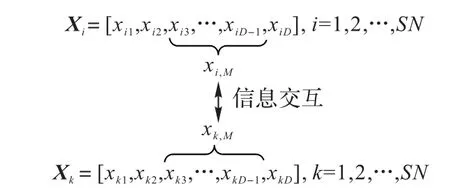
图1 多维匹配更新示意图Fig.1 Schematic diagram of multi-dimensional matching update

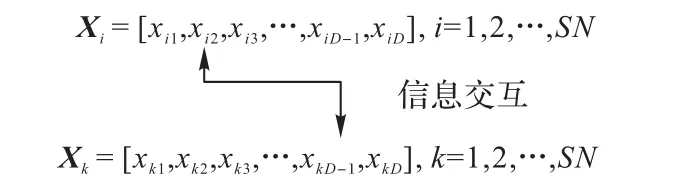
图2 异维单点更新示意图Fig.2 Schematic diagram of different-dimensional single point update

2.3 雇佣蜂组合策略CS1

对于标准ABC 算法，雇佣蜂主要借助式（2）在当前解i的邻域内进行一次扰动，主要包括三个随机项j、k、φi，j，随机项j确定某一具体更新维度，随机项k确定用于更新的另一个解，这种更新模式使初始解仅在对应的同一维度内更新邻域，虽然表现出一定的全局探索性，但局部开发性较弱。因此，为达到立体式搜索效果，采用一种组合策略CS1 来平衡算法的探索和开发能力。

CS1-1 搜索方程中包含了四个随机项M、k、h、φi，j，加强广度探索：

其中：M是多维匹配更新的维度数；k≠h≠i且k，h∈{1，2，…，SN} 是随机选择的个体下标。M个维度的多维匹配更新在最大限度上保留了初始解的有效信息，同时在一定程度上保证了邻域搜索的均衡性，而随机项k、h提高了解在邻域内的探索能力，扩大了搜索空间，即CS1-1策略兼顾了雇佣蜂邻域搜索的广度与深度。

CS1-2侧重于深度开发，与文献［20］中式（3）“vi，j=xbest，j+φi，j(xbest，j-xi，j)”不同，式（5）避免了xbest，j与xi，j差距过大时导致的扰动过大，最大限度保留了精英个体的有益信息，提高了搜索效率。

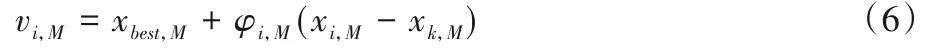
其中：xbest是每一代中适应值最高的精英个体。

雇佣蜂随机选择CS1-1 和CS1-2，在全局探索的同时兼顾对最优个体的开发。

2.4 跟随蜂种群划分

在跟随蜂阶段，将种群划分为自由子集和非自由子集，如图3 所示。为两类个体赋予特定的职能，其中自由个体适应值与精英个体适应值相差较大，潜在的开发效益较差，可以加强其探索能力来搜索额外的解空间；非自由个体的适应值与精英个体的适应值的差异较小，有更好的挖掘潜能，可以赋予其在非自由子集范围内的开发能力，以加强算法在优势个体的深度搜索。跟随蜂中非自由个体搜索通常情况下比自由个体搜索跨度要小，两种策略的结合在深度和广度上加强了算法的搜索能力。

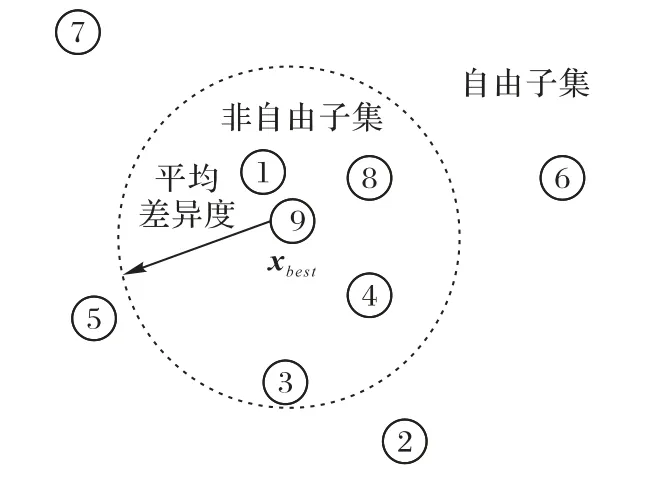
图3 种群划分Fig.3 Population division

平均差异度dt作为划分种群的依据：

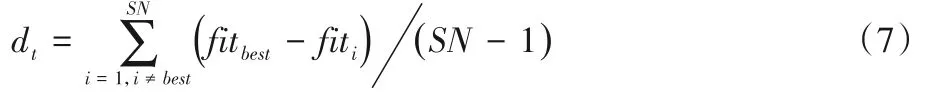
其中：dt是第t代循环适应值的平均差异度；fitbest和fiti分别是精英个体和第i个体的适应值。

计算当前个体适应度fiti与最佳个体适应度fitbest的差值，比较差值与平均差异度dt的大小，若差值大于平均差异度，即超出以平均差异度为半径的范围，则当前个体视为自由个体；反之，当前个体视为非自由个体，以此来进行种群划分。

2.5 跟随蜂组合策略CS2

在跟随蜂阶段，经过轮盘赌选择后，当跟随蜂选择的是自由个体，通过两个随机个体和当前个体构建探索的子策略CS2-1，包括M、p、q、φi，j四个随机项，使其在整个解空间内进行随机搜索：

其中：p≠q≠i且p，q∈{1，2，…，SN} 。

非自由个体具有成为下一精英个体的潜在优势，而多源信息交互是改善搜索性能的有效手段，因此，当跟随蜂选择的是非自由个体，则通过当前个体、精英个体和非自由子集中的随机个体构建CS2-2 子策略，在非自由子集范围跨越维度深度开发，以期发现未知的优势个体：

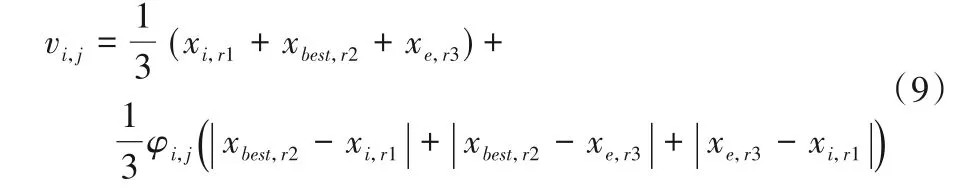
其中：xe是非自由子集中的随机个体；r1≠r2≠r3且r1，r2，r3∈{1，2，…，D} 。

式（8）与文献［20］中式（12）在方程结构上很相似，需要注意的是，在文献［20］中式（12）是利用精英解的有益信息和同维单点更新机制，相应的，式（8）采用的是非自由子集中随机个体的有益信息和异维单点更新机制，在扩大有益解空间的同时有效利用了异维信息的协同优化。

2.6 MCABC流程

算法迭代过程中，雇佣蜂随机选择子策略CS1-1 或CS1-2更新初始化种群个体，通过与初始化种群贪婪选择保留当前优势个体；以个体适应值和最佳适应值的平均差异度比较作为种群划分标准对当前优势个体进行种群划分，为跟随蜂阶段作准备；通过轮盘赌方式对跟随蜂进行选择，针对自由子集跟随蜂采取CS2-1子策略，非自由子集跟随蜂采取CS2-2子策略，在进行贪婪选择后更新自由子集和非自由子集；对于达到未更新次数的个体进行初始化。不断循环上述过程，直到满足算法停止条件，算法流程如图4所示。

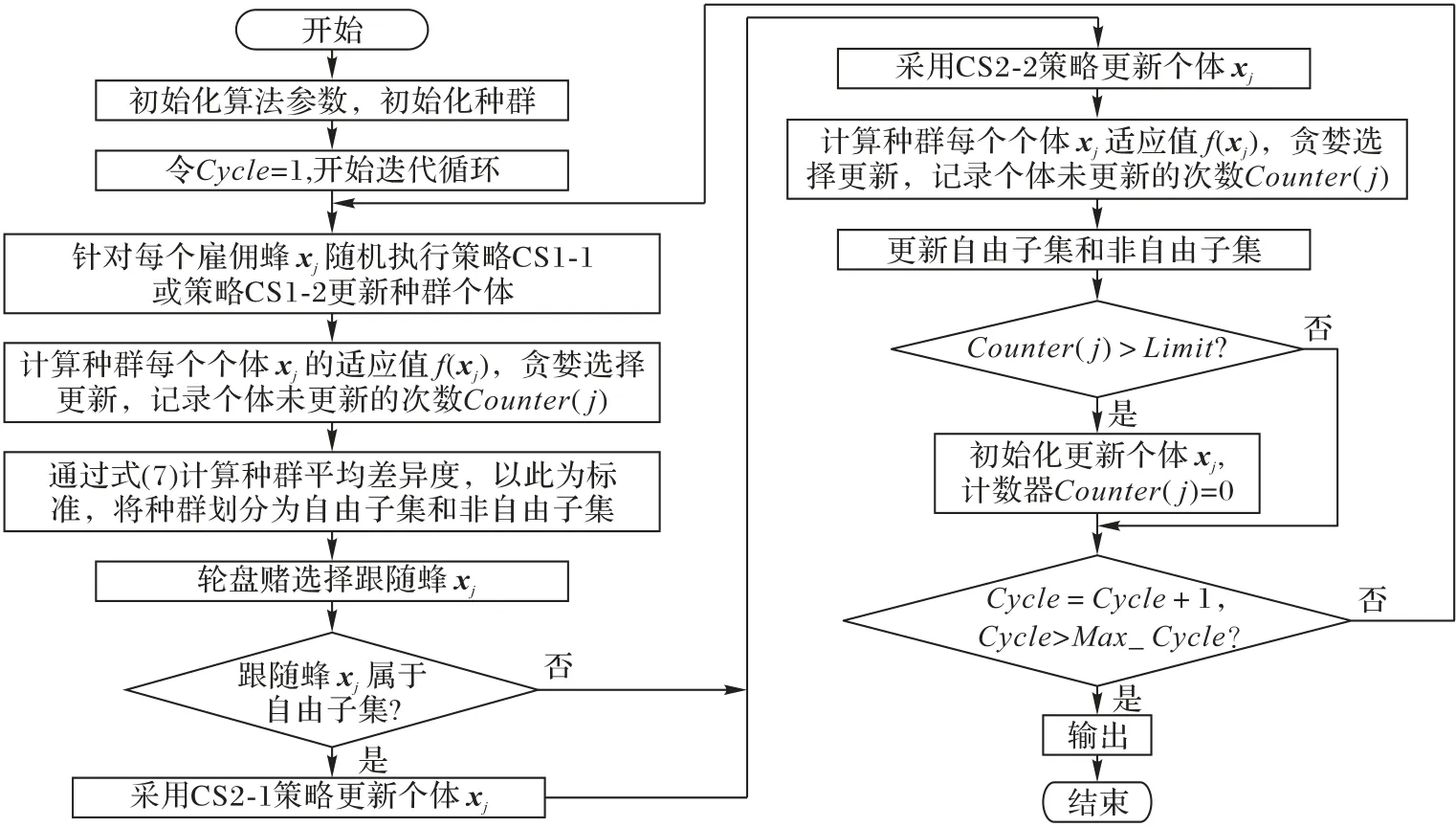
图4 MCABC算法流程Fig.4 Flow chart of MCABC algorithm

2.7 MCABC伪代码

MCABC伪代码如下：

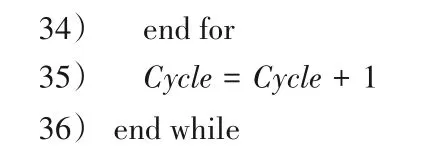
2.8 算法复杂度分析

MCABC 算法在雇佣蜂阶段和跟随蜂阶段分别引入了两种不同的种群更新策略。在雇佣蜂阶段，种群个体通过随机方式选择策略CS1-1和策略CS1-2进行更新，该过程不增加算法的时间复杂度。在跟随蜂阶段，涉及循环前的种群整体划分和循环中的种群动态划分，在循环前，需依据种群个体适应值和精英个体适应值的平均差异度作为种群划分的标准，首先依据适应度值对整个种群进行排序操作（对总体排序）选择出精英个体，其时间复杂度为O（SN·log（SN）），然后通过式（7）计算种群平均差异度，以此标准对种群整体进行划分；在循环过程中，每次循环后需判断当前更新个体是否为精英个体，更新当前个体后通过式（7）计算种群适应值的平均差异度来动态划分种群，该过程不涉及排序操作，不额外增加算法的时间复杂度。

因此，与ABC 算法相比，MCABC 算法在雇佣蜂阶段开始前划分种群过程时引入了额外的计算，由于ABC 算法的时间复杂度为O（SN·D），因此，MCABC算法时间复杂度为O（SN·D+SN·log（SN）），由于D远大于log（SN），MCABC 算法的时间复杂度可以简化为O（SN·D），可见相较于经典ABC 算法，MCABC算法具有相同的计算时间复杂度。

3 实验仿真与结果分析

3.1 测试函数实验结果

为了测试本文提出MCABC 算法的性能，采用15 个标准测试函数，将MCABC与文献［4］提出的ABC、文献［25］提出的GABC（Gbest-guided Artificial Bee Colony）、文献［26］提出的qABC（quick Artificial Bee Colony）、文献［27］提出的CABC 四种算法进行比较，仿真基于Matlab 2016a 软件平台实现。测试函数信息如表1所示。

表1 标准测试函数Tab.1 Benchmark functions

仿真在一台搭载1.6 GHz 的Intel Core i5 处理器和4 GB内存的PC 平台上实现。考虑对算法性能进行较为全面的测试，采用的15 个测试函数包括了各种类型的特征函数，f1、f2、f4、f6～f8、f12为连续单峰函数，在解空间中仅有一个极值点；f3在特定的间隔产生阶跃现象，是一种不连续的阶跃函数；f5的特征与问题的维数有关，当D≤3 时，f5为单峰函数，当D>3时，f5为多峰函数；f9～f11、f13～f15为连续多峰函数，在解空间中存在大量的局部极小值点，该类函数在求解时易陷入局部最优。算法实验参数设置如下：蜂群规模NP=60，算法最大迭代次数MCF=5000，未更新限制次数Limit=3000，为了测试算法在低维和高维条件下求解性能的差异，分别在函数为50维和100 维时进行测试。比较算法的特定参数均参照原文设定［2-3］：qABC 中r=1.5，GABC 中C=1.5。对每个测试函数运行20次，得到最优值（Best）、平均值（Mean）、方差（Std）及达到可接受值的平均迭代次数（Minc），50 维和100 维仿真结果如表2～3所示

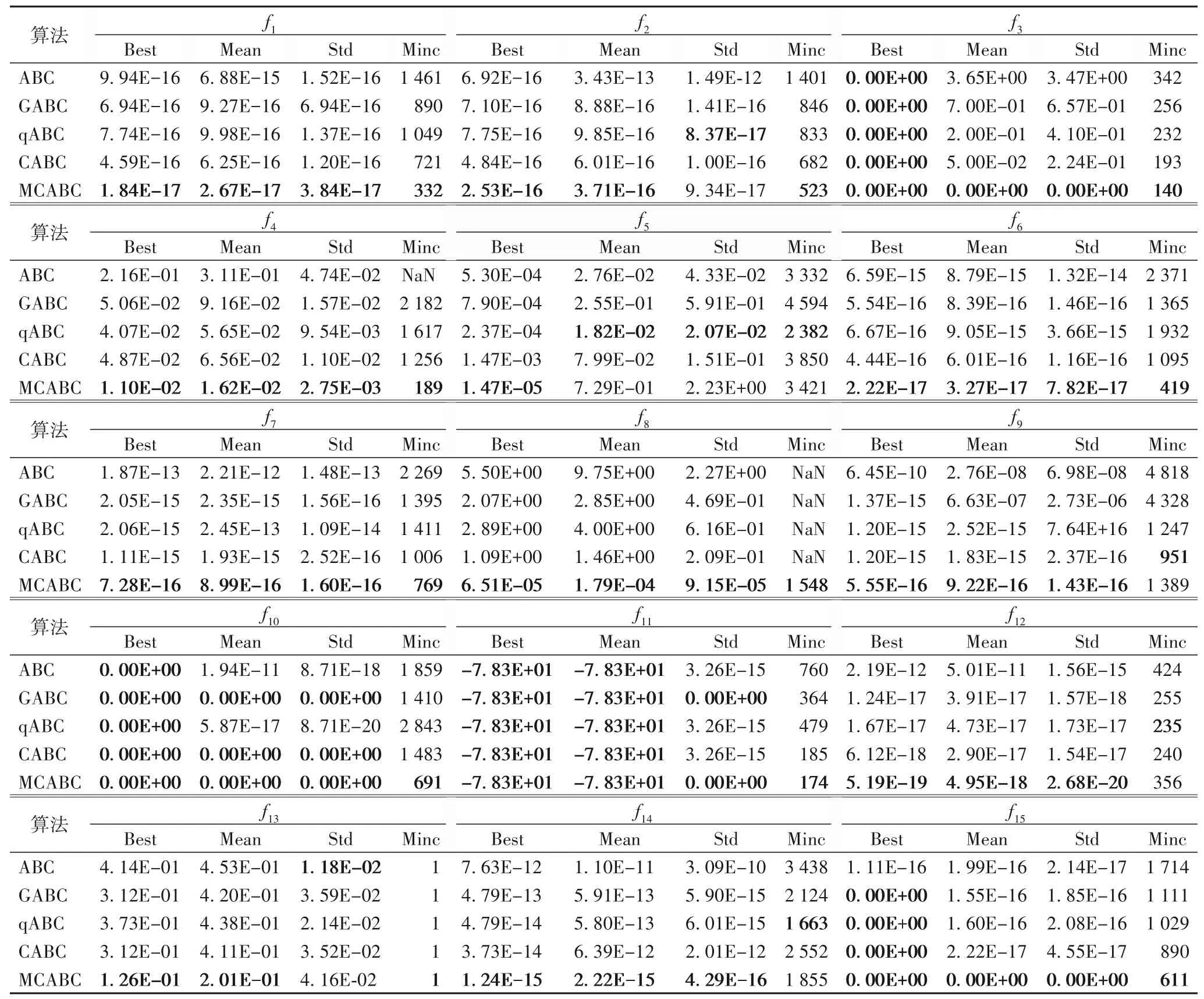
表2 低维函数下5种算法的仿真结果（D=50）Tab.2 Simulation results of five algorithms under low-dimensional functions（D=50）

本文采用4 个评价指标对各算法的性能进行对比，Best（Mean）表示20 次独立测试中的最佳目标值（平均目标值），Std（Minc）记录了20次独立实验测试结果的标准差（达到可接受值的平均迭代次数）。表2 记录了D=50 的测试结果。与标准ABC 相比，对于除f3、f10以外的所有函数，MCABC 在收敛速度、求解精度、稳定性上均优于ABC，由于f3全局最优是一个区域，f10全局最优不是一个点，因此这两个函数更容易搜索到最优值，所以MCABC 与ABC 都能够求得最优值，但MCABC 在收敛性和稳定性上显著优于ABC。此外，在函数f8、f9、f12、f15的求解中，MCABC的求解性能远优于ABC。MCABC 与其他改进ABC 相比，在求解精度上，对于函数f3、f10、f11、f15，MCABC 与其他改进ABC 均能达到最优值，在除f3、f10、f11、f15以外的其他函数上，MCABC 在求解精度上均不同程度优于其他改进ABC。在算法稳定性上，qABC 在f5上优于MCABC，特别对于函数f10，GABC、CABC 与MCABC 均具有最强的稳定性，在函数f11的求解中，GABC 和MCABC 也具有相同的强稳定性，在除f5、f10、f11外的其他函数上，MCABC 均优于其他改进ABC。在算法收敛性上，qABC 在f5、f12、f14略优于MCABC，CABC 在f9优于MCABC，在除f5、f12、f14、f9外的其他函数上，MCABC 均远优于其他改进ABC。综上，在50 维函数测试条件下，MCABC的综合寻优能力优于已有的改进ABC。

为进一步验证本文改进算法在高位函数中的有效性，选择文献中常用的4 个具有代表性的测试函数在100 维条件下进行仿真，结果如表3所示。

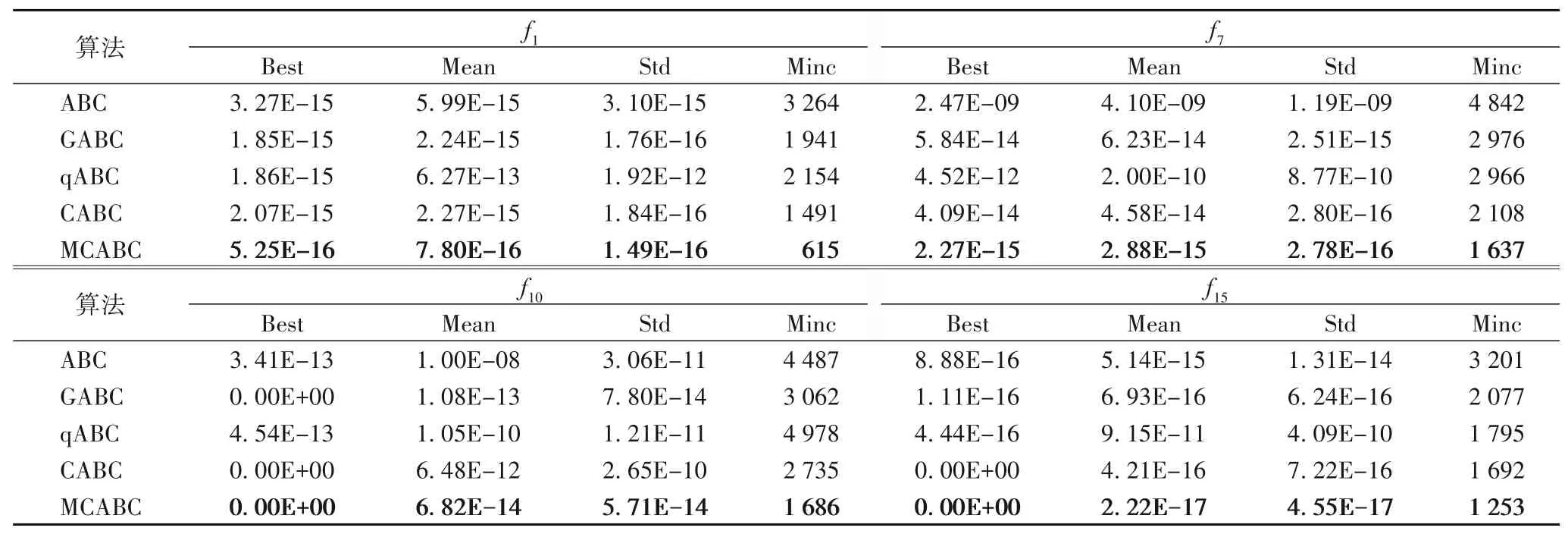
表3 高维函数下5种算法的仿真结果（D=100）Tab.3 Simulation results of 5 algorithms under high-dimensional functions（D=100）

由于MCABC采用多维匹配和异维协同的更新机制，因此MCABC 在收敛精度上均超过其他算法，尤其是对于函数f10、f15，MCABC 尽管在稳定性上不如低维条件下好，但是依旧能收敛到理论最优。100 维测试下MCABC 相较于ABC 及其他改进算法在收敛速度上具有显著优势，并且在稳定性上均优于其他算法。为更加可视化展示MCABC的求解性能，选取不同类型的四个函数f1、f7、f10、f15，分别在50 维和100 维条件下对5个算法进行对比，如图5～6所示，其中，收敛函数图是本次独立实验的收敛函数曲线。

由图5～6 可以看出，得益于搜索方程更新模式的多样性，无论在低维还是高维测试中，MCABC 收敛速度均明显快于其他算法，且收敛精度最高，均保持良好的下降趋势。在50 维测试条件下，改进4 种ABC 算法能够有效发挥各自不同的优势，下降速度和趋势差异较为明显；在100 维测试条件下，由于维度的显著增加，受限于搜索方程更新模式的单一性，削弱了改进ABC 算法各自的优势，各改进ABC 算法的下降趋势和收敛速度相对接近，收敛曲线差异性减小，但MCABC 仍旧保持相较于其他算法的显著优势。

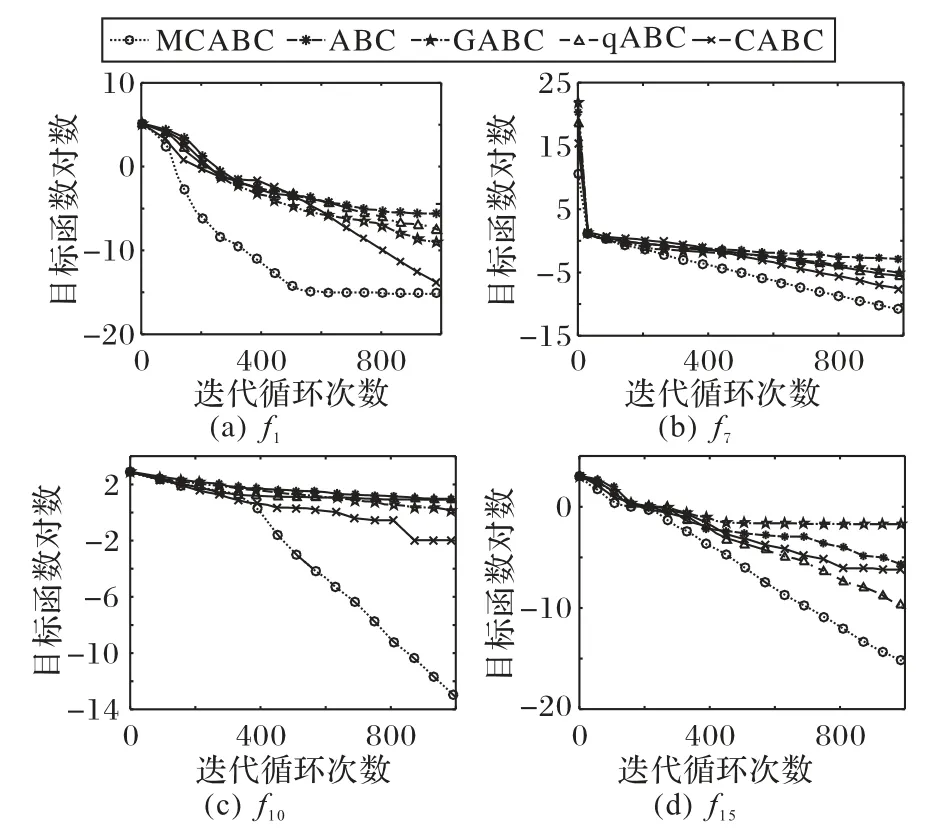
图5 四个标准测试函数的50维收敛图Fig.5 Fifty-dimensional convergence graph of 4 benchmark functions

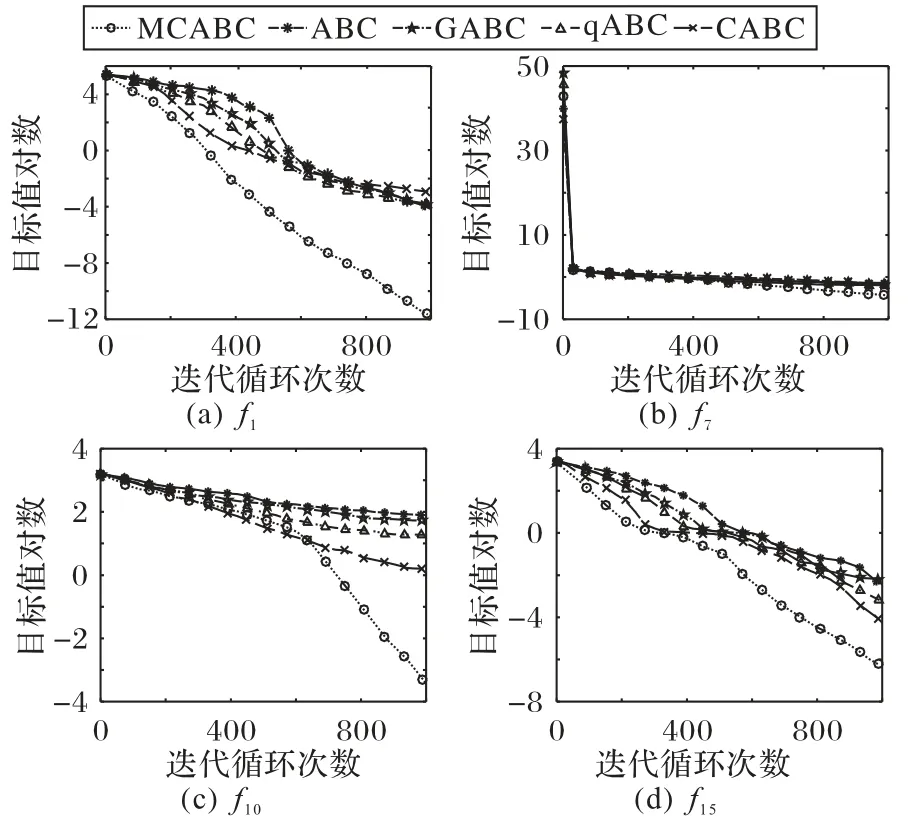
图6 四个标准测试函数的100维收敛图Fig.6 One hundred-dimensional convergence graph of 4 benchmark functions

3.2 算法的运行时间

为了检验MCABC 的时间复杂度，在相同的运行环境下，计算各算法的运行时间，计算得到15个算法在D=50条件下的平均运行时间如表4 所示。由表4 可以看出，由于MCABC与ABC 的时间复杂度相差不大，故在运行时间上略有增加，而MCABC相较于其他三种比较算法在运行时间上均有降低。因此，本文提出的寻优方法在可接受的计算时间内能够有效提高算法的求解质量。

表4 不同算法运行时间对比 单位：sTab.4 Running time comparison of different algorithms unit：s

4 结语

本文提出了一种基于多种群组合策略的人工蜂群算法，通过将多维匹配和异维协同两种更新机制引入搜索方程，提高了算法更新模式的多样性；同时，分别针对雇佣蜂和观察蜂提出了两个组合策略，以平衡算法的广度探索和深度搜索，并在雇佣蜂阶段划分自由子集和非自由子集，以明确个体的搜索重点。通过对标准测试函数进行仿真实验，进一步验证了本文所提出的MCABC算法具有良好的寻优性能。