以自动化码头为中心的船舶配载优化

丁 一，王聪

（上海海事大学物流研究中心，上海 201306）

0 引言

在全球经济一体化的大趋势下，各国集装箱货物的海运量呈爆发式增长，世界集装箱船队的数量也在不断增加，船舶也逐渐向大型化、专业化和标准化发展，一方面提高了船公司的规模效益，另一方面给码头带来了更大的挑战，传统集装箱码头也正逐步向半自动化和全自动化过渡。

自动化码头在传统码头的基础上，优化了工艺布局。如图1 所示，自动化码头将传统码头平行于海岸线的堆场箱区布局改进成垂直于海岸线的堆场箱区布局，同时在每个箱区增设了固定的发箱点，解决了传统码头发箱区域规划紊乱、发箱效率低下的问题。在堆场设备上，自动化码头采用了轨道吊（Rail-Mounted Gantry crane，RMG），替代了传统码头的轮胎吊（Rubber-Tyred Gantry crane，RTG），RTG 可以跨箱区作业，但在多个RTG 作业时，容易在公共作业区域发生冲突，而RMG则是各箱区专用，发生的冲突较少。

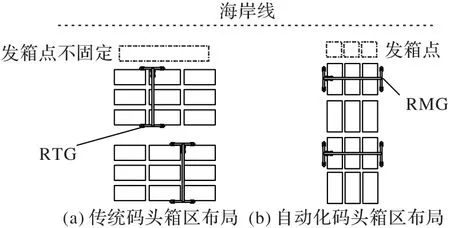
图1 传统码头与自动化码头箱区布局Fig.1 Block layouts of traditional terminal and automated terminal

在当今码头集装箱货物运输的各个流程中，配载作为其中的核心环节之一，对自动化码头的作业效率和安全、船舶在港时间以及货方收益等方面都有着直接影响。配载作业流程如图2 所示，一般分为两个阶段：第一阶段是船舶公司制定的预配载计划（分类/详细的预配载箱位图）；第二阶段是将预配载计划作为输入数据，由码头运营商制定的码头配载计划。

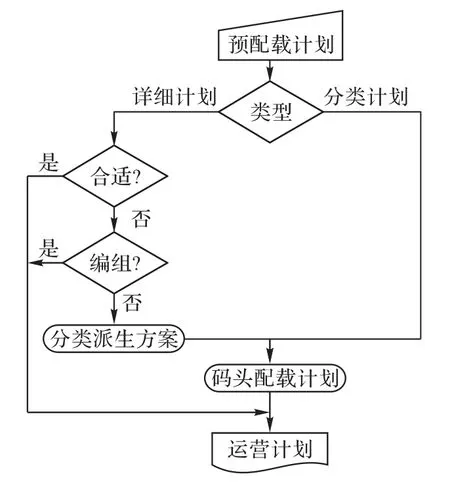
图2 配载作业流程Fig.2 Flow chart of stowage operation

1 相关工作

目前大部分的配载优化研究主要是从船公司和码头这两个方面考虑的。

船公司方面注重如何减少多港口运输装卸所导致的翻箱问题以及船舶航行中的安全问题，如计明军等［1］围绕配载方式进行分析，总结四种配载方式在船舶稳性、强度和吃水差等方面的优缺点，以此来分析减少翻箱率的方法；而乐美龙等［2］考虑翻箱和桥吊的作业时间，并以此建立整数规划模型，使得翻箱次数最少和桥吊工作时间跨度最小。

在考虑船舶靠泊时间成本因素后，Serban 等［3］在待卸集装箱数量和箱区的初始状态已知的情况下，以最小化场桥的搬运时间总和为目标，利用遗传算法确定集装箱配载计划；而田维等［4］研究船舶装箱排序问题，将最小化装船时间以及翻倒箱时间成本作为目标，对不同规模案例进行求解，获得问题的精确解；Roberti等［5］则在满足许多操作限制的同时，尽量减少在港口装卸集装箱的时间，使得集装箱最大限度地减少不必要的配载作业。

为了提高集装箱航线动态装载自动调度的能力，Wang［6］提出了一种基于关联规则信息的集装箱航线动态装载自动调度方法；郑斐峰等［7］针对翻箱费用和堆栈使用费用，以船舶装载稳定性作为约束条件，求得最小化费用的精确解；黄森佳等［8］综合考虑集装箱船舶纵向强度、岸桥作业安全距离和集装箱倒箱量对装船作业时间的影响，构建了以装船作业时间最短为目标的配载优化模型，引入岸桥作业均衡参数，并使用遗传算法对模型进行求解；孙俊清等［9］以最小化集装箱班轮在所有停靠港口的总倒箱量为目标，将船舶稳性作为约束条件，使用改进的遗传算法进行求解，并通过仿真实验比较了两种配载方案。

码头方面考虑装船作业时间的缩短以及配载结果保证船舶航行安全，如：黎明等［10］结合集装箱的装载位置，以集装箱堆场的翻箱率、船舶卸载时的翻箱率以及装船后的稳性为目标，建立了装船顺序的多目标规划模型；张兆民［11］通过“关键相邻柜口”的配载计划优化、作业拖车数量的增加和分级堆场堆存等操作策略的执行，可有效控制“关键相邻柜口”的作业时间，缩短船舶在港作业时间；祝慧灵等［12］以翻箱问题为切入点，致力于保证配载计划完成的前提下，建立三种提箱顺序优化策略来达到翻箱量最小的目标；Zhao 等［13］考虑堆场周转、轮胎吊跨箱区作业和轮胎吊移动，基于配载原理和约束，建立多目标优化模型，建立蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）方法，根据搜索树设计可拓、可选等5 个步骤及相应策略；李隋凯等［14］针对带中转排的自动化码头出口箱进箱选位问题，提出了一种两倍状态多阶段动态规划算法；周宇涛等［15］通过运用逻辑算法，设置配载策略和参数，快速进行深度运算提高配载精度，更好地满足船公司差异化配载要求。

两个角度研究的考虑因素、模型和方法如表1所示。

表1 不同角度船舶配载考虑因素、模型和方法对比Tab.1 Comparison of ship stowage considerations，models and methods from different perspectives

通过上述的文献分析可知，目前大多数的研究集中于从船公司的角度出发，考虑常规约束（吃水差、稳性和船体强度约束等）、翻箱问题和装船时间等，从码头角度出发的研究较少，考虑的也多是翻箱问题、堆场堆存问题和配载装船时间等；但由于自动化码头箱区的发箱点固定，需要保证各设备的合理高效使用，避免出现设备等待拥挤的情况，只考虑这些问题无法保证集装箱的高效装卸，也无法最大化利用自动化码头的设备资源。因此，本文在考虑常规约束的基础下，引入箱区作业均衡性这一因素，从码头的角度出发，对自动化码头的装船配载作业来进行分析研究。

2 问题描述

从自动化码头的角度来说，配载问题一般可以分成三个子问题。结合右侧图3 自动化码头配载作业图来看，第一个是集装箱由外集卡装载通过闸门，进入堆场箱区，在哪个箱区箱位落位的箱位问题；第二个是堆场待装集装箱装船的先后顺序问题，即将集装箱从堆场运至岸侧桥吊工作区的先后顺序问题；最后一个是集装箱分配的船箱位问题，即集装箱在船上放置的位置问题。从位置①-②-③-④-⑤-⑥，即算完成配载计划中一个待装集装箱的装船作业任务。

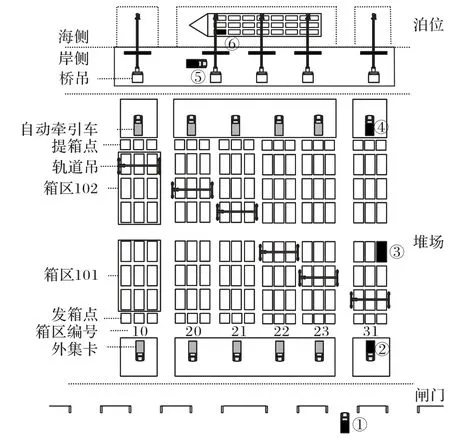
图3 配载作业图Fig.3 Stowage operation diagram

首先，对于集装箱的箱区箱位问题来说，无非就是如何极大化地方便装船作业，并且充分利用到堆场的自动化设备资源，确保在装船作业过程中设备闲置率较低，提升堆场集装箱作业效率。

其次，是装船先后顺序问题，顾名思义就是决定堆场箱区待装集装箱装载到运输船舶的排序问题。在装船作业顺序问题上，不得不提到翻箱问题，装船过程中某些集装箱存放在箱区的其他集装箱下方，由于待装船舶的到来，如果下方集装箱需要优先提箱，则会先移动该集装箱的上方集装箱，再提取下方的集装箱。具体的翻箱过程可结合图4，描述如下：堆场箱区集装箱i位于同贝同列不同层的集装箱j的上方，任务1 是将箱区集装箱i由A 点运输至船舶B 点上，任务2 是将箱区集装箱j由C 点运输至船舶D 点上，由于配载船图上显示集装箱i在船舶的箱位仍位于集装箱j的上方，所以要先执行任务2，而且需要先将集装箱i移动到箱区其他位置，这就形成了一次翻箱。

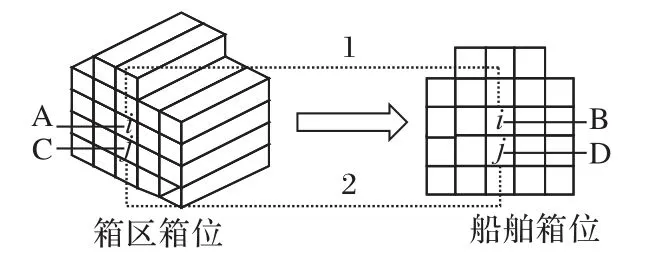
图4 翻箱示意图Fig.4 Schematic diagram of rehandle

而对于集装箱分配的船箱位问题，就是解决集装箱离场后的去处，即安排在哪一船舶箱位的问题，以便于在下一个卸货港减少翻箱量，快速完成卸货任务。

从图5可以得知，配载问题作业时间是由翻箱时间、RMG提箱时间、自动牵引车（Automated Guided Vehicle，AGV）运输时间和桥吊（Quay Crane，QC）作业时间组成的。配载问题的目标在于减少从箱区箱位到船舶箱位的作业时间，从而减少船舶在港的停留时间，节约成本。

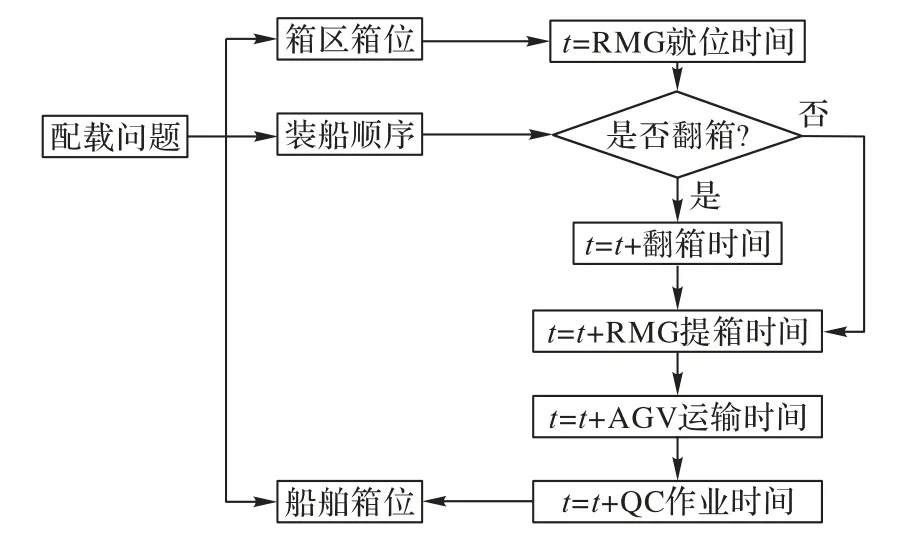
图5 配载流程Fig.5 Flow chart of stowage

另外，在自动化码头堆场中，如果同一时间段内箱区的装卸作业量相差过大时，就会导致箱区作业不均衡问题：一方面，对于装卸量偏大的箱区，这些箱区的轨道吊连续工作时间过长，轨道吊的故障率上升，而且由于箱区的轨道吊作业能力有限，一旦提存箱的指令过于集中，可能会导致轨道吊作业冲突；另一方面，对于装卸量偏小的箱区，闲置的轨道吊没有得到充分利用，单位成本上升。因此，对于箱区作业量均衡的研究很有必要。

3 模型建立

3.1 参数

i，j为待装集装箱号，i=1，2，…，I，j=1，2，…J；k为贝位号，k=1，2，…，K；c为列号，c=1，2，…，C；r为层号，r=1，2，…，R；b1为箱区编号，b1=1，2，…，B1；b2为箱区区块编号，b2=1，2，…，B2；b3为小箱区编号，b3=1，2，…，B3；b为箱区具体编号，b=(b1，b2，b3)；p为待装集装箱的船箱位，p=1，2，…，P；εp为箱位p的开始装箱时间；U(p)为位于船舶箱位p(k，c，r)同贝同列上一层p(k，c，r+1)的箱位；t为表示t-1到t的时间间隔，t=1，2，…，T，∀t∈T；wi为集装箱i的重量；nbt为t时间段内箱区b已完成场到船任务的集装箱数量；Δi为与集装箱i同一堆栈的上层集装箱集合；α为箱区一个待装集装箱不考虑翻箱的场桥平均作业时间（场桥就位和取箱平均时间）；βbt为t时间段内箱区b作业量与各箱区平均作业量的差值比例值，其计算式为βbt=为t时间段内所有箱区集装箱作业量的平均值；ρ（ρ>0）为箱区作业不均衡判定比例值；σ1为堆场箱区一次翻箱时间；σ2为不均衡箱区的集装箱单位等待惩罚时间；W为船舶贝位中单列允许的集装箱最大载重量；τip为集装箱i从场箱位到船舶箱位p(k，c，r)的水平运输时间；BLTip为安排到船箱位p的在场箱i在箱区的离开时间，BLTip=εp-τip，其中∀i∈N，p∈P；φbt为箱区b在时间段t的箱区作业量阈值；γip为二维0-1 变量，按待装船集装箱i是否符合预配图要求从而配载到船舶所对应的船舶箱位p(k，c，r)，满足为1，否则为0；θip为二维0-1 变量，若待装船集装箱i位于箱区b，则对应的元素为1，否则为0；M为一个极大的正数。

3.2 决策变量

xip为0-1 变量，集装箱i从箱区离场，且被安排在船舶箱位p(k，c，r)则取1，否则为0；zij为0-1变量，当集装箱i先于j离场时取1，否则为0，其中∀i∈N，j∈Δi；δbt为0-1 变量，箱区b在t时间段的作业不均衡判定变量。δbt可表示为：

3.3 假设条件

假设条件如下：

1）目前船舶在码头的配载作业有单船配载作业和多船配载作业两种，本文研究的是单船配载作业，且为了避免装卸同时进行时设备冲突的增加以及翻箱数的上升，不考虑边装边卸。

2）考虑到船公司一般会为特种箱安排特定的船箱位，配载会严格遵循，即使船公司没有严格说明，也应遵循特种箱的一般装载要求，因此本文仅考虑普通箱的配载。

3）本文的视角是从自动化码头出发的，预配载计划由船方制定，卸船较为方便，且有临时存放点可以加快卸船速度，因此本文研究的是码头方装船配载方案的优化。

4）配载是船方与码头方的协同工作，预配船图需由船方提前给予码头方，了解集装箱的各种信息，如尺寸大小等，且本文主要集中于堆场部分的研究，因此假设已知船舶预配总图、桥吊作业计划和待装船的在场箱信息。

3.4 目标函数及约束

以f为目标函数，建立以集装箱船舶装船作业时间最小为目标的优化模型，即：

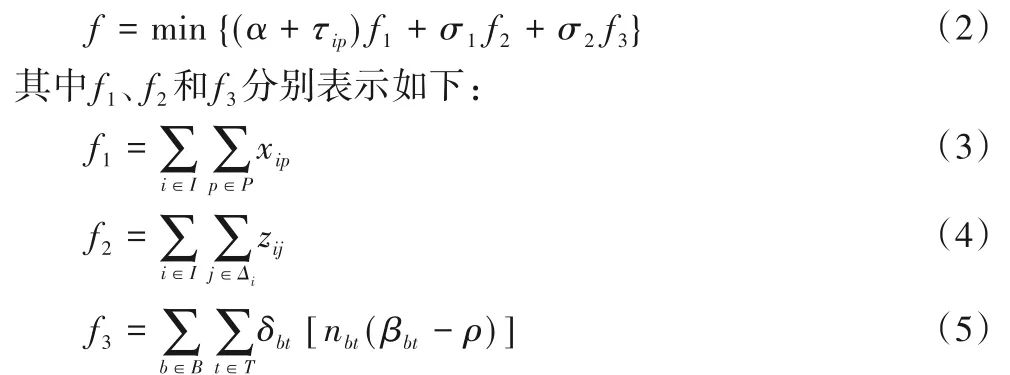
其中：目标函数式（3）表示待装集装箱的离场数；式（4）表示翻箱次数；式（5）表示箱区作业不均衡判定次数。

另外，约束条件为：

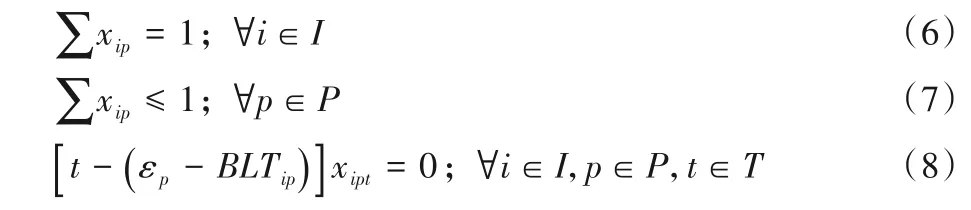
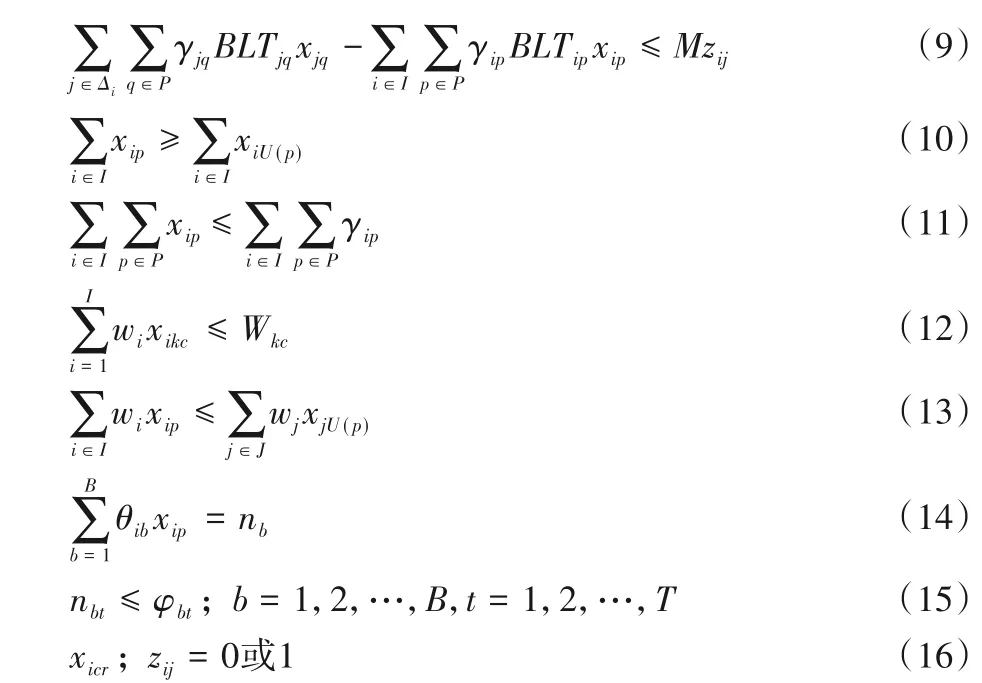
其中：约束（6）～（7）为箱位限制约束，即一个集装箱只能被安排到一个有且只有一个船舶箱位中；约束（8）表示待装集装箱离开箱区必须符合桥吊作业的时间安排；约束（9）表示位于同一堆栈不同层数的待装集装箱离开箱区的先后顺序和翻箱的关系；约束（10）表示待装集装箱在船舶箱位紧挨着的下方有集装箱即不能悬空；约束（11）表示待装集装箱与船舶贝位的匹配满足预配要求；约束（12）表示船舶同贝同列集装箱的装载重量不能超过单列额定重量；约束（13）表示箱区集装箱轻不压重的堆垛要求；约束（14）表示确保离场集装箱数量与待装集装箱数量相同；约束（15）表示箱区作业量限制，防止作业量过大；约束（16）表示决策变量类型。

4 基于固定集搜索算法的模型求解方法

集装箱船舶配载问题本身是一个NP-hard 问题，同时通过上述模型部分描述可知该问题也是一个多目标、多约束的组合优化问题。当船舶配载的集装箱装卸数量较少时，可以通过Cplex 计算出较优解，但随着船舶大型化的发展、自动化码头的不断扩容以及自动化设备的更新迭代，集装箱装卸的数量一般是较大的，在这种情况下，运用Cplex 求解计算时间会较长或直接无法得出较优解。因此，本文根据实际情况设计了基于固定集搜索（Fixed Set Search，FSS）算法的模型求解方法。

4.1 基本原理

固定集搜索算法是在贪婪随机自适应搜索过程（Greedy Randomized Adaptive Search Procedure，GRASP）［16］中加入学习机制的一种算法，其重点在于避免专注于特定的较优解，而是专注于这些解中的部分元素，通过固定多次出现在较优解中的部分元素，致力于寻找固定部分元素组后的最优解。

4.1.1 前提条件

使用固定集搜索算法需要满足两个前提条件：

前提一 通过固定所得解集中的部分解，可以降低正在搜索的解集空间大小，缩短目标函数完成时间；

前提二 有一部分高质量的解集中的固定解容易识别，不需要通过过多的比对。

4.1.2 贪婪随机自适应搜索

随机组合箱区箱位和船舶箱位一一对应来形成解集，在匹配组合过程中，将已经确定的组合放入一个集合中，直至该集合包含所有的待装集装箱的安排组合，检查是否符合约束条件，符合再计算目标函数的结果，记录目标解与解集，如此反复，每次排列完需要对解集进行检索，是否为已有解集，是否是新的最优解。

4.1.3 固定集

通过固定出现在大量较优解集中相同的部分组合，形成固定的部分解的集合，以此来缩小搜索空间，当然固定集的形成需要满足三个条件：

条件一 生成的固定集需要包含高质量的解集的部分解；

条件二 一个生成的固定集至少能够用来生成一个可行解；

条件三 固定集的规模是可以控制和变化的。

固定集具体的表现形式如图6所示。

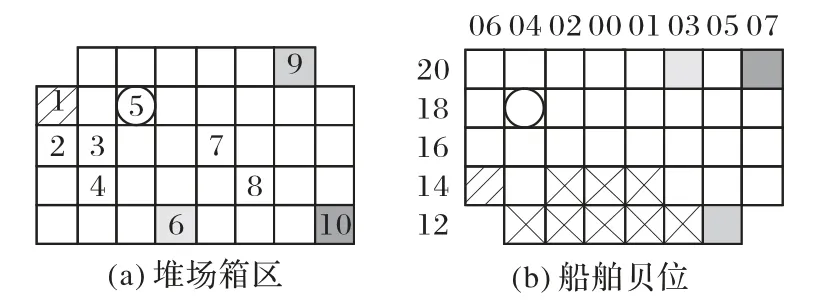
图6 固定集表现形式Fig.6 Expression form of fixed set

图6中，数字1～10代表箱区的待装集装箱，带有相同特殊标记的区域代表堆场与船舶位置的固定，未带标记的需要进行继续组合搜索，船舶贝位中打“×”的代表位置已有其他集装箱存放。从图6得知，箱区1号集装箱已固定存放至右侧船舶贝位06 列14 层中，5 号集装箱固定至该贝位04 列18 层中，6 号集装箱固定至该贝位03 列20 层，9 号集装箱固定至该贝位05列12层，10号集装箱固定至该贝位07列20层。

4.1.4 算法终止准则

算法的终止判定条件如下：

1）首先，判断最优解搜索是否已经停滞，如果是，将固定集规模大小设置为下一个值，需要注意的是如果当前固定集规模大小已经是最大值，则返回最小值。

2）接着，更新固定集规模大小前，检验在寻找高质量解时是否出现了停滞，如果停滞，即使用固定集所得解不是更优解，再检验所得解是不是已知最优解集合中的一个解，如果不是，且这个固定集规模大小还是最小值，则将当前固定集规模大小从固定集规模大小的集合中移除。

3）最后，当固定集规模大小的集合为空集时，则增加迭代次数，达到最大迭代次数时，终止算法。

4.2 算法设计

4.2.1 参数设置

船舶配载的相关数据包括：具体的箱区在场箱数量与可用船箱位数量，箱区在场箱的箱位位置与船舶箱位位置，集装箱各自对应的卸货港、货物的尺寸以及船箱位的桥吊开始作业时间等，这些数据都是自动化码头和船方分别提供匹配出来的结果。因此解的表达式需要包含两者的信息，采用第一行“i”行的码头箱区集装箱信息与第二行“p”行的船舶箱位信息一一对应的方式来表示，解的具体表达形式如下：

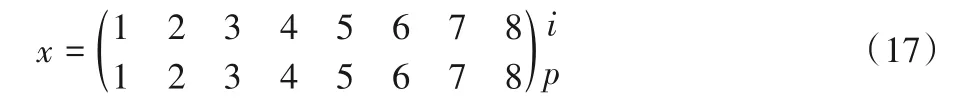
码头与船方箱位信息的对应关系如图7所示。

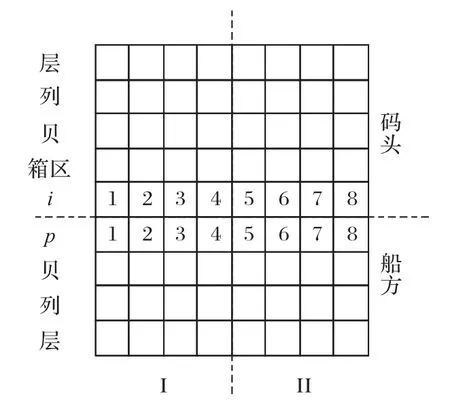
图7 码头与船方箱位信息对应解的形式Fig.7 Corresponding solution form of terminal and ship’s slot information

4.2.2 搜索改进

由于贪婪随机搜索的随机性过强，计算时间可能较长，需对搜索方法进行改进。在搜索初始可行解时，使用随机的集装箱与船舶箱位匹配，扩大可行解的搜索范围，对不满足约束的解进行二次匹配，改为邻域交换和平滑匹配（首尾依次匹配）。

根据实际情况，其实待装集装箱是有许多不同属性的，如尺寸不同、卸货港不同等，一般相近属性的集装箱是存放在较近的位置的，为了避免跨度较大，对所有的同贝同层不同列的待装集装箱进行划分处理，将前一半归为I 类，后一半归为II类，基于预配载为初始参考解，如图8 所示，将I类和II类分别进行邻域交换和平滑匹配，对同类同贝同层不同列的集装箱进行位置的交换，交换后的解仍然满足预配和轻压重约束，以此来寻找与预配结果持平或比预配更好的解。

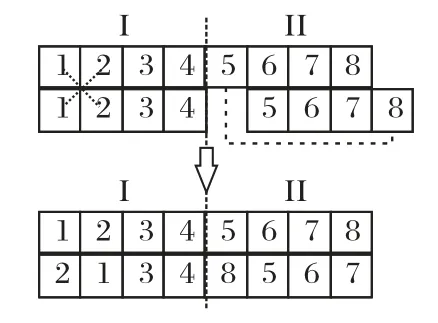
图8 箱位匹配Fig.8 Slot matching

4.3 基本步骤

4.3.1 参数定义

算法参数的具体定义如下：

P表示所有生成解（总体）的集合；Pn定义为n个最优解的集合，Pn=Selectn(P)；D为最大迭代次数；Skn定义为从Pn随机选取k个解的集合，Skn=Selectk(Pn)，Skn={S1，S2，…，Sk} ；B为从m个最优生成解的集合Pm中任意选取一个随机解B，其中，B=Select(Pm)，B={e1，e2，…}且B∈Pm，e1代表一个箱位安排；V代表待装集装箱总数；C(ex，S)为0-1 变量，如果ex属于S为1，否则为0；O(ex，Skn)表 示ex在Skn中出现的次数，Sizes为固定集规模大小集合，Sizes[i]=|V|-，其中i为大于0 的整数，用来根据当前所得解对Sizes大小进行更改；F为能够在搜索中使用固定集，具体的表达式为F=Fix(B，Skn，Sizes)，表示大小为Sizes、初始解B中在Skn中出现最多次的箱位安排；S表示使用固定集F而得到的解，S=RGF(F)；T表示生成解的目标函数值集合。

4.3.2 具体步骤

在对固定集搜索算法中的一些参数进行定义并得到基本解之后，就可以利用算法对基本解进行迭代优化，首先获得初始基本解，通过迭代得到初始可行解，最后通过迭代获得能够接受的最优解。具体的迭代步骤如下：

步骤1 设置模型与算法参数，将箱位可安排集合设为Candidates，待装集装箱总数为V，确定最大迭代次数D，且初始迭代次数d=0，固定集集合为F，固定集大小集合为Sizes，固定集大小为Size，固定集大小影响参数为i，集合为I，且初始参数i=1，最大值为Imax，GRASP中的箱位交换初始次数为f=0，最大交换次数为fmax，解的集合为P。

步骤2 输入初始基本解x0（船方提供的预配数据），当前解xf=x0。

步骤3 判断当前解xf是否满足堆场箱区作业量阈值和船舶单列最大重量约束，即判断是否为可行解，是则进入步骤5，否则进入步骤4(GRASP)。

步骤4 进入步骤4.1；

步骤4.1 将同卸货港同尺寸大小的集装箱（箱位）作为同一类别集装箱（箱位）进行处理，提取当前输入数据的集装箱的所有类别CC，在每一个类别中，提取该类别中的所有贝位CB和层数CT，进入步骤4.2；

步骤4.2 记录层号CT中存在两个及两个以上集装箱的层号为Tier，进入步骤4.3；

步骤4.3 随机交换Tier中两个集装箱的位置，记录f=f+1，得到新的箱位排列，生成当前解xf，返回步骤3。

步骤5 计算当前解xf的目标函数值Vf，其中Vf=Value(xf)，将各个目标函数值放入集合T，将当前解xf放入解的集合P，判断是否f大于等于fmax，是则进入步骤6，否则返回步骤4。

步骤6 记录迭代次数d=d+1，判断当前迭代次数d是否大于等于最大迭代次数D：若是，则算法结束，比较各个最优解BSd和最优函数值BSVd，输出在迭代D次之后的最终最优解UBSd和最优函数值UBSVd；否则进入步骤7。

步骤7 从n个最优生成解的集合Pn中随机选取k个解得到Skn，从m个最优生成解的集合Pm中任意选取一个随机解B，固定集大小为Sizes[i]，进入步骤8。

步骤8 利用F=Fix(B，Skn，Sizes)，确定固定集F，剔除Candidates中固定集F的箱位安排，即排除掉已经确定位置的箱区箱位位置和船舶箱位位置，根据同卸货港和箱位尺寸进行箱位安排生成解S，S=RGF(F)，进入步骤9。

步骤9 判断当前解S是否满足约束，即判断是否为可行解：若是，进入步骤11；否则进入步骤10。

步骤10 进入步骤10.1；

步骤10.1 更新输入数据的集装箱的所有类别NCC，同一类别中提取更新后的所有贝位NCB和层数NCT，进入步骤10.2；

步骤10.2 记录层号NCT中存在两个及两个以上集装箱的层号为NewTier，进入步骤10.3；

步骤10.3 在NewTier中任选一个层号，计算该层待装集装箱数量num，选定划分位置mod(num，2)，前一半邻域交换，后一半平滑匹配，进行箱位交换，得到新的箱位排列，生成当前解S，返回步骤9。

步骤11 计算解S的目标函数值VS=Value(S)，将解S加入到生成解集合P，将VS与集合T中最小值Tmin比较：若VS更小，则i=i+1，且记录当前最优解BSd=S，最优函数值为BSVd=VS，将VS加入T，进入步骤15；否则进入步骤12。

步骤12 判断S是否为Pn或Pm中的一个解：若是，则i=i+1，进入步骤15；否则进入步骤13。

步骤13 判断i是否为当前影响参数集合的最小值Tmin：若是，则从I中删除当前i，进入步骤14；否则i=i+1，进入步骤15。

步骤14 判断I是否为空集：若是，则f=0，返回步骤2；否则i=i+1，进入步骤15。

步骤15 判断当前i是否大于Imax：若是，则i=Imin；否则i不变，返回步骤7。

5 算例分析

本文根据上海某集装箱码头的实际配载数据进行分析，通过FSS与Cplex 的算例计算结果对比以及固定集搜索算法、粒子群优化（Particle Swarm Optimization，PSO）算法、遗传算法（Genetic Algorithm，GA）和蚁群优化（Ant Colony Optimization，ACO）算法之间的算例计算结果分析，验证本文所提模型与FSS 的有效性。实验所使用的电脑配置为Windows 1064 位操作系统，8 GB 运行内存，处理器为Inter Core i5-8265U，CPU 频率为1.6 GHz，使用软件为IBMI LOG Cplex Optimization Studio 12.2和Matlab 2018a。

5.1 数据说明

本文将上海洋山港某码头提供的配载数据作为实例研究，整理出6组规模不等的实例，详细的数据说明如表2所示。其中，箱量是数据梳理后的待装集装箱数量，箱区数表示这些待装集装箱所属的不同箱区数，LD 表示该组实例的待装集装箱在堆场箱区中最左下角的位置，RU表示该组实例的待装集装箱在堆场箱区中最右上角的位置，2D 表示同一实例中只有2 个集装箱的堆栈数比例，3D 表示同一实例中只有3 个集装箱的堆栈数比例。

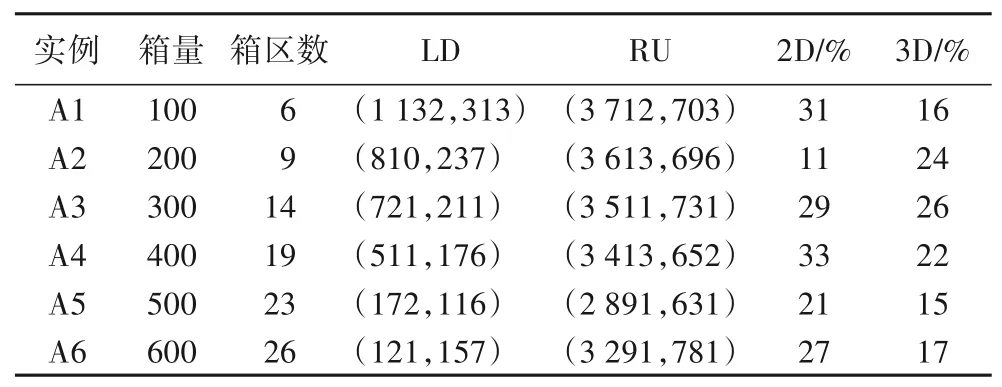
表2 实例数据说明Tab.2 Data description of real instances

首先为了方便统计数据将时间段t设置为1 h，作为单位时间段，参考上海洋山深水港四期自动化码头的实际配载数据来确定模型的部分相关参数，设定箱区单位时间内的最大作业箱量为20 箱，箱区一个待装集装箱不考虑翻箱的场桥平均作业时间即平均场桥就位和取箱时间为2 min，箱区的一个待装集装箱从堆场到桥吊工作区的水平运输时间为3 min，箱区内一次翻箱时间为3 min，箱区不平衡可能导致的集装箱单位惩罚时间定为2 min。模型参数确定后，运用Cplex 对模型进行求解。鉴于问题复杂性较大，可能导致Cplex 无法求解，因此设定Cplex 的最大运行时间为1 h，同时设定算法的相关参数如下：最大迭代次数D=50，固定集大小的影响参数最大值Imax=10，GRASP中的箱位最大交换次数fmax=200。

5.2 实例结果分析

在参数ρ=0.5的情况下，FSS 与Cplex 的实例求解的最终解结果如表3所示。

表3 不同算法实例计算结果的对比Tab.3 Computational result comparison of different algorithms on real instances

表3 的实例计算结果包括翻箱量、不均衡程度、目标函数值和求解时间，在计算中，由于Cplex 求解模型的限制，将Cplex 的求解时间设定为1 h，求解结束后返回目标值，若超过1 h，则无最优结果。首先，对Cplex 与所提算法两者的求解时间作了对比，从表3 可以看出，箱量从100～600 箱的6 个实例中，所提算法的计算时间在18.7 s～161.6 s，而Cplex最短计算时间为178.1 s，仍超过了算法的最大计算时间，尤其箱量为600 时Cplex 计算时间超过了1 h，显示无结果，相比之下FSS却有着很好的求解结果和求解效率。相较于Cplex，FSS 求解的翻箱数和不均衡箱数都较小，实例A5 减少了最多的7 次翻箱，且实例A5 减少了最多的13 个不均衡箱数；FSS 的目标函数值一直是较小，最大差距74 min，只有规模较小的实例A1两者计算的差距不大，最小差距42 min。综上，不同规模的实例下，FSS 算法相较于Cplex，翻箱量和不均衡箱数分别平均减少了22.3%和11.7%，目标函数值平均优化了6.5%。

5.3 不同算法对比

鉴于Cplex求解的时间较长且存在无法求解的情况，增加粒子群优化（PSO）算法、遗传算法（GA）和蚁群优化（ACO）算法对案例的计算分析，与本文所提的固定集搜索算法进行比较，参数ρ取0.5，粒子群算法PSO 的种群规模取200，最大迭代次数为50，惯性权重为0.7189，加速常数为1.1503；遗传算法的种群规模取200，最大迭代次数为50，以目标函数的倒数作为适应度值，交叉概率为0.9，变异概率为0.3；蚁群算法的种群规模取200，最大迭代次数为50，信息因子为1，期望因子为5，信息挥发因子为0.1。详细的数据对比见表4。

从表4 可以看出，在箱量较小的案例中，各算法的四个指标差距不大，且在案例A1 中，遗传算法的目标函数值最小为348 min，不均衡箱数和求解时间也是最低的，分别为16 箱和17.9 s；但随着箱量的增加，翻箱次数和不均衡箱数的差距不断拉大，固定集搜索算法的优势逐渐显示出来，四个指标的值一直是最小值。总的来说，相较于其他三种算法，固定集搜索算法的稳定性更好，在翻箱数和不均衡箱数的优化上更优，求解的质量更高，目标函数值平均优化了2.1%。

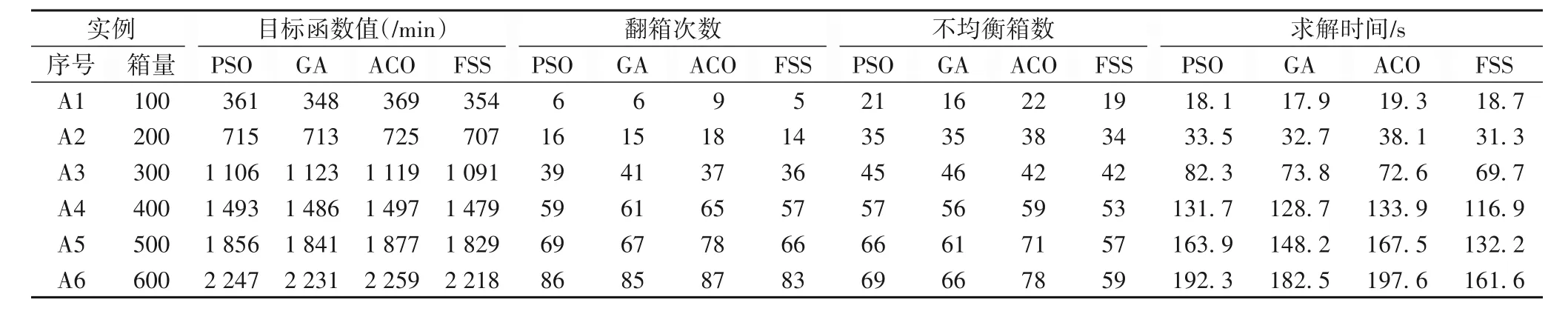
表4 不同算法的优化结果对比Tab.4 Optimization result comparison of different algorithms

5.4 虚拟案例分析

鉴于实例数据缺少变化性，需要对实例的数据进行处理分组，增加一些不同情况下的虚拟案例进行分析研究。与此同时，为了更加方便直观地了解港口的运作情况，根据洋山港四期提供的数据对自动化码头进行模拟布局，具体布局如图9所示。

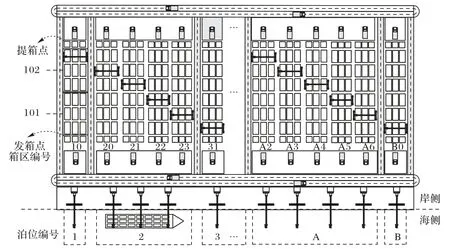
图9 算例配载箱区图Fig.9 Instance stowage block diagram

由图9 可知，箱区的区域范围是很大的，箱区从1 到B 有11个箱区，这11个箱区可以分成122个小箱区，如101就是箱区10 的第一个小箱区，根据距离待装船舶的远近对箱区进行分类编号，如表5所示。

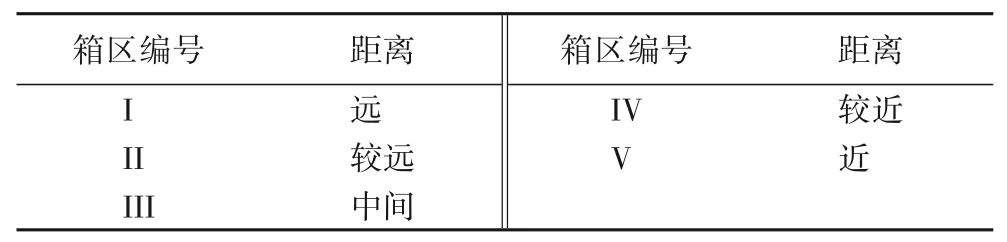
表5 箱区距离编号Tab.5 Number of block distance

接下来，对实例进行如下处理，构成虚拟案例，进行多样性分析：

1）重新安排同一实例中具有2 个和3 个待装集装箱的堆栈分布；

2）将实例中有2个和3个的集装箱堆栈比例进行调整。

第一步，堆栈分布按照箱区距离待装船舶的距离远近进行正态分布处理，如图10所示，横坐标d表示箱区与待配载船只的距离，纵坐标代表那些待装集装箱的分布概率n，越靠近作业船舶的待装集装箱概率就越大，但n值也有最大值为M，用来避免集装箱数量过多，码头负荷运作。随着距离d变化的集装箱分布概率n的正态分布函数表示为：

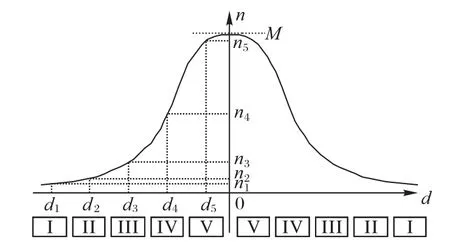
图10 箱区待装集装箱正态分布Fig.10 Normal distribution of containers to be loaded in block

根据码头箱区集装箱分布的实际情况，取μ为0、σ为，则M为1，将分布概率控制在区间［0，1］。

第二步，调节堆栈比例，堆栈配置所示如表6所示。

表6 堆栈配置Tab.6 Configuration of stacks

每组堆栈配置下进行两次正态分布的待装集装箱安排，则每组实例如箱量为100 的A1 就有a1、a2、b1、b2、c1、c2 这6个虚拟案例分析，由于数组过多，取6 个虚拟案例的平均值作为每一组的比较数据，具体的计算结果如表7所示。

表7 虚拟案例计算结果Tab.7 Computational results of virtual instances

由表7 可知，虚拟案例将待装集装箱的堆场箱位集中在距离待装船舶较近的箱区，四个指标数据都高于原本的实例数据，但差距不是很大。固定集搜索算法依旧优于其他三种算法的计算，目标函数值平均减少了22 min，翻箱次数平均减少了16.1%，不均衡箱数最多减少了16 箱，求解时间平均减少了14.7 s。

6 结语

传统码头与自动化码头在布局、设备与作业工艺等方面的不同，导致自动化码头在配载问题上需要更多考虑设备与场地的充分利用。为了减少码头的运营成本，快速完成配载工作，因此以最小化翻箱次数、箱区集装箱作业量的不均衡程度和总装船时间为目标，建立相应的配载优化模型，设计固定集搜索算法进行求解，且分别通过与Cplex、粒子群算法、遗传算法和蚁群算法的对比，验证了本文所提固定集算法的高效性。与此同时，为了增加算例的多样性，设置了虚拟案例，与另外三种算法相比，固定集搜索算法的不均衡箱数平均减少了19.3%，目标函数值即总装船时间平均减少了22 min，求解时间平均减少了14.7 s。

综上，无论是在求解效率还是在求解效果方面，本文所构建的自动化码头船舶配载混合整数规划模型与固定集搜索算法都有较优的配载结果，缩短了码头装船时间与船舶靠泊时间，为后续不确定情况下的船舶配载优化研究提供参考。