浅谈高中数学中立体几何解题技巧

闫海新

摘 要：立体几何是高中数学教学内容的重要组成部分，是学生必须掌握的主要知識之一，是提升学生直观想象核心素养的主阵地。学生通过立体几何的学习，增强空间几何感和空间想象力，提升逻辑思维能力和表达能力。本文将提供三种常规的立体几何体积的解题思路，通过这三种常规解题思路逐步加强学生对立体几何的掌握程度。

关键词：高中数学;立体几何;解题方法

美国数学家哈尔莫斯说：“数学的真正组成部分应该是问题和解，解题才是数学的心脏。

”教育家波利亚称：“掌握数学就意味着善于解题。”立体几何知识的掌握和运用，能力的提高当然离不开解题和克服解题中的问题。因此，师生必须加强立体几何的学习，提高学习效率。

一、适当分割，多个求和

一般的数学考题中，关于体积的计算，不会是一个简简单单的长方体、正方体或是三棱锥，而是几个长方体、正方体的结合形成的多面体，求它们相结合形成的体积。在此类型中，最常见的解题方法就是分割法，把多面体分割成几个我们常见的立体几何。然后，分别求出每个分割体的体积。最后，将所有的分割体体积相加，就能得出总体积了。例如，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF//AB，EF=1.5，EF与平面AC的距离为2。那么，该多面体的体积是多少？在本题中，由于多面体ABCDEF是一个不规则的立体几何图形，我们无法用常见的立体几何的体积算法，去计算该多面体ABCDEF的体积。此时，我们便可以运用分割法的知识，将多面体ABCDEF分割成常见的立体几何，再进行计算。我们先连接BE、CE构成一个新的平面BCE，这个平面将多面体ABCDEF分割成了四棱锥E-ABCD和三棱锥E-BCF。此时，多面体ABCDEF的体积就等于四棱锥E-ABCD的体积加上三棱锥E-BCF的体积。教师可以引导学生得出V=V+V，在进行求解。

二、两把利刃，三视图和直观图

从三视图和直观图研究几何体是分析视图的常用方法，也是培养空间想象能力的重要途径.从空间中某一点观察几何体，找出几何体关键点、线、面要素，从宏观整体感知几何体的形状，建立几何体的实际模型，再微观从正视、侧视、俯视三个方面观察几何体，更准确地感知几何体的构造，利于分析解决问题。

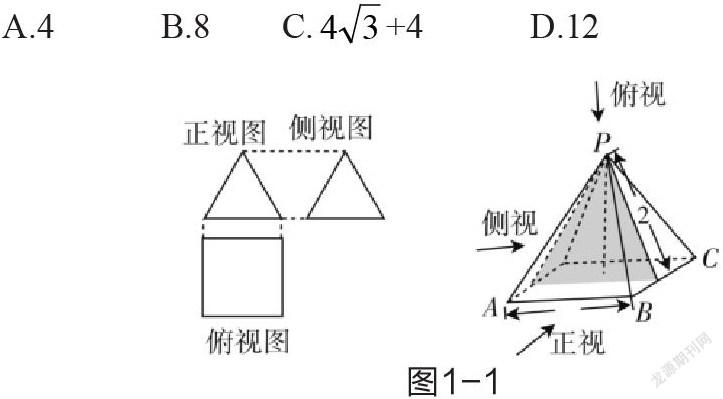
例如，如图1-1，一个简单空间几何体的三视图，其正视图与侧视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其全面积是（ ）。

A.4 B.8 C.+4 D.12

分析：本题多数学生初学时会认为侧棱即为斜高，导致侧面积计算错误。引导学生从三视图概念分析，结合具体四棱锥实物模型，再次观察各视图形状和和直观图中的点与线段关系，从而获得正确的数据，再让学生画出对应的四棱锥直观图并在图上标出三视图中对应的尺寸，完成解题。

感悟：三视图反映几何体在某个面上的投影形状，直观图反映几何体整体性质，掌握直观图和三视图的画图规则。能从空间几何体的直观图确定三视图形状，从三视图想象它的直观图，在教学中重视实物模型-三视图—直观图之间的相互转化，训练空间立体感促进想象能力的发展。

三、动态研究，面体互化

几何体是多个平面围成或者平面图形绕轴旋转产生的，是平面几何知识的延伸和升华，从而有些立体几何的问题可以转化为平面几何问题来分析，借助平面图形知识来解决。

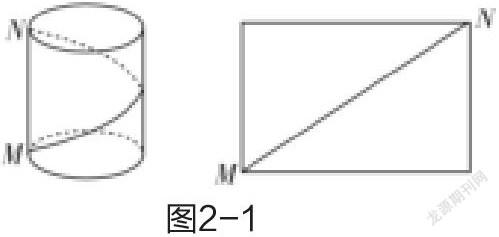
例如，圆柱的底面半径为1，母线长为2，点M，N在同一条母线上，且分别位于上，下底面，求点M绕圆柱的侧面到N的最短路径长.

分析：要求绕圆柱的侧面运动的最短路径，化曲为直，沿母线MN将圆柱侧面剪开展得矩形，则最短路径即为矩形对角线长。

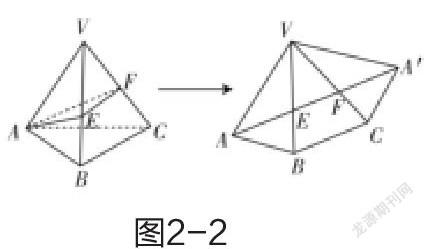
变式：如图2-2，在三棱锥V-ABC中，VA=VB=VC=2，∠AVB=∠BVC=∠CVA=40°，过A作截面AEF分别交VB，VC于点E，F，求△AEF周长的最小值。

分析：本题即在棱锥中求三个侧面上线段AE+EF+FA的和，空间中的和最短常转化为平面和最短问题，则沿AF展开侧面，变成从A到A′的距离最小值即可。

感悟：空间中在不同面研究距离、面积等问题可以结合几何体的结构特征在空间和平面之间转化思考，把几何体表面或侧面展开，利用平面几何知识来解决.

结语

总之，高中立体几何作为高考考查的重要知识点之一，必须在教学中培养高中学生的空间想象能力和解题能力。教师要让学生把立体几何当中的知识点理清楚。然后，在一般的基础上理解体积计算的各种方法，明白每一种方法之间的变通，让学生在实践过程中能运用这些巧妙的方法，更好地掌握该知识点。

参考文献

[1]魏文艳.处理立体几何问题，常规方法不可忽视[J].数理化解题研究，2014（12）：35.

[2]王晓峰.高中立体几何解题教学研究[D].内蒙古师范大学，2013.

[3]蒋平.立体几何教学之我见[J].中学数学月刊，2012（9）：62.