不平衡数据下基于PSO-BP算法的输电线路弧垂预测

李嘉雨 廖如超 李钰楷

0 引言

架空输电线路弧垂是输电线路风险评估与载流量校核的关键因素．现有的弧垂计算方法一般是通过收集架空输电线路的档距、高差、温度、风速等数据,使用抛物线法或悬链线法计算得到的,但与激光点云测得的真实弧垂值误差较大[1-2]．而普通的BP神经网络应用在弧垂预测方面会面临数据缺失、精度不高、训练速度较慢等问题．本文在现有的弧垂计算模型基础上,使用合成少数过采样技术(Synthetic Minority Oversampling Technique,SMOTE)对不平衡样本进行合成[3-6],利用粒子群优化算法(Particle Swarm Optimization,PSO)优化BP神经网络,构建PSO-BP神经网络,建立弧垂的预测模型,并与传统BP神经网络方法进行比较,结果表明本文提出的模型可以加快训练速度、提高预测精度．

1 算法原理

1.1 SMOTE算法

SMOTE 算法[7-9]全称为合成少数过采样技术,它可以针对不平衡样本的少量数据集通过合成新数据的方式进行过采样．SMOTE算法的具体原理如下:

(1)

式中,xj为xi的N个近邻样本中的第j个样本,rand(0,1)为小于等于1、大于等于0的随机值．SMOTE算法示意如图1所示．

图1 SMOTE算法示意Fig.1 Schematic diagram of SMOTE

1.2 粒子群优化算法

粒子群算法的数学模型如下:

每个粒子都在N维空间内进行搜索,当适应度值发生改变时,粒子会根据不同的适应度值更新自己的速度．适应度值每变化一次,粒子的速度和位置就更新一次．多次迭代直到达到终止条件获得最优解．粒子通过下列公式[10-12]来更新自身速度和位置:

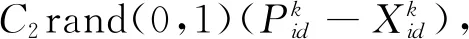
(2)

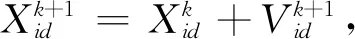
(3)

式中：k为迭代次数；ω为惯性因子，ω的值可以影响局部寻优性能和全局寻优性能；C1和C2为加速常数,前者为每个粒子的个体学习因子,后者为每个粒子的学习因子．C1和C2为常数时可以得到较好的解,一般取C1=C2∈[0,4],本文中取C1=2,C2=2．rand(0,1)为小于等于1、大于等于0的随机值,Pid,Pgd分别表示第i个变量的个体极值的第d维和全局最优解的第d维．

1.3 BP神经网络

在BP神经网络的正向计算过程中,分析数据的特征以确定输入神经元的节点数并输入数据,然后以不同的权重计算,神经元通过sigmoid函数被激活,数据向隐含层传播,在隐含层通过计算后,神经元以同样的形式被激活,将数据传递给输出层[13-15]．如果输出层的输出与标签(label)值存在误差,则计算误差并生成协方差函数,且将误差反向传播,通过误差修正各个节点的权值和阈值,达到减小误差的目的．

1)正向传递

设节点i和节点j之间的权值为ωij,节点j的阈值为bj,每个节点的输出值为xj,则每个神经元的具体计算方法如下:

(4)

xj=f(Sj),

(5)

式中,f为sigmoid激活函数．

2)误差反向传播

在BP神经网络中,dj为输出层的所有结果,协方差函数为

(6)

在本文提出的方案中,BP神经网络在训练的过程中将不再运用反向传播方法,取而代之的是使用PSO算法优化[16-17]．

2 基于数据预处理的PSO-BP神经网络弧垂预测算法

首先将采集的数据进行预处理,对于温度和风速这两个缺失较多的数据使用SMOTE算法进行数据合成,将架空输电线路档距和高差这两个线路特征以及温度、风速这两个气象特征作为BP神经网络的输入参数,设计合适的隐含层节点数以及一个输出层节点作为弧垂值的输出节点,以弧垂真值作为标签(label)值,构建协方差函数,即PSO算法的适应度函数[18-24]．

弧垂预测模型的具体步骤如下:

1)数据合成．设定SMOTE算法的相关参数，确定采样倍率N和近邻数k的值,使用数据合成方法对温度和风速数据集进行扩充．

2)初始化．首先初始化PSO算法的种群规模、粒子维数等参数，然后确定BP神经网络的输入数据为架空输电线路的档距、高差、温度、风速,针对4个输入确定BP神经网络各层的节点个数,初始化PSO算法的粒子．

3)初始适应度获取．BP神经网络在输出层与标签(label)值对比,生成协方差函数,PSO算法使用该函数计算适应度值．

4)PSO算法执行．每个粒子在每次更新自己的适应度值后,对比个体最优值,将个体最优值更新为二者中的最小值;在更新后将该值与全局最优值进行对比,将全局最优值更新为二者中的最小值．

5)粒子通过式(2)和(3)计算自己新的速度和位置．

6)判断是否满足算法终止条件,不满足返回步骤3),满足条件则结束算法．

PSO-BP神经网络的算法逻辑流程如图2所示．

图2 PSO-BP算法流程Fig.2 Flow chart of the proposed PSO-BP neural network algorithm

3 实验仿真

3.1 实验数据

实验数据采用我国南部某地区的架空输电线路数据,共260条记录,每条记录包括5个属性:架空输电线路档距、架空输电线路高差、环境温度、环境风速、输电线路弧垂．本实验以前4个属性为预测模型的输入属性,输电线路弧垂作为预测属性．

3.2 实验结果

建立Input-Hidden-Output结构的3层神经网络,对该网络进行初始化:根据输入数据的4个属性设置4个输入节点,输出只有1个弧垂值,故设置1个输出节点.根据神经网络隐含层节点计算公式设置6个隐含层节点,设粒子更新最大代数为1 500,最小适应度值1×10-3,学习速率0.01．根据PSO算法,设置规模为60的粒子种群,惯性因子设为1,对于学习因子,设C1=2,C2=2．

建立弧垂预测模型并测试、训练,所得结果如图3所示．由图3可知,PSO-BP神经网络对弧垂的预测值有很优良的表现,且算法性能优于传统BP神经网络

图3 PSO-BP与传统BP神经网络预测弧垂与弧垂真值对比Fig.3 Comparison of sag prediction between PSO-BP and traditional BP neural network

图4中,PSO-BP神经网络在迭代次数为120时达到最优．

图4 适应度曲线Fig.4 Fitness curve of the proposed PSO-BP neural network

3.3 性能对比

将PSO-BP神经网络与传统BP神经网络的仿真结果进行对比,得到2种神经网络对架空输电线路的弧垂预测结果以及与真值的误差,数据如表1所示.

表1 PSO-BP和传统BP模型对弧垂值预测的结果Table 1 Sag prediction results obtained by traditional BP and PSO-BP model

图5中实线为传统BP神经网络预测的弧垂值与真值的误差曲线,虚线为PSO-BP神经网络预测的弧垂值与真值的相对误差．显然,PSO-BP的弧垂预测模型的误差小于传统的BP神经网络的误差．

图5 相对误差曲线Fig.5 Comparison of relative error between PSO-BP and traditional BP neural network

4 结论

对于架空输电线路弧垂预测存在计算误差较大，且气象数据较少等问题,本文提出了针对不平衡数据下基于PSO-BP算法的输电线路弧垂预测．对收集数据中部分样本缺失的情况,使用合成少数过采样技术(SMOTE)对不平衡样本进行合成;构建PSO-BP神经网络对架空输电线路的弧垂进行预测．本文算法性能较传统BP神经网络有明显优势,有效预测了架空输电线路的弧垂值,提高了弧垂预测的准确性．