随机分布参数切换系统的输入输出有限时间稳定与镇定
左凰 戴喜生 邓飞其
0 引言
系统的稳定性是控制科学中的一个非常重要的研究课题.通常人们关注系统在无穷时间区间上的行为,如渐近稳定[1]、指数稳定[2]等,系统状态在运行足够长的时间后会恢复到平衡态.但对于实际应用而言,具有Lyapunov稳定的系统在有限的时间区间内很可能存在不良的瞬态性能,因此有限时间稳定性分析对系统在给定时间区间内的暂态性能的表现有重要意义.Dorato[3]于1961年首次提出了短时间稳定的概念,这是有限时间稳定概念的雏形.随后吸引了大量学者对系统的有限时间稳定性进行研究[4-6].2010年,Amato等[7]延续了传统的有限时间稳定概念,针对线性时变系统提出了新的概念即输入输出有限时间稳定,指的是满足零初值条件的系统运行在给定时间区间上,给定一类有界的输入信号,系统的输出在该时间区间内始终不会超出给定的界.由于输入输出有限时间稳定的系统具有良好的抗干扰性[8]和鲁棒性[9],因此在提出后受到了极大的关注.输入输出有限时间稳定也因此推广到更广泛的系统中,如分数阶系统[10]、切换系统[11]、脉冲系统[12]等.
随机分布参数系统是一类由随机偏微分方程描述的无穷维随机系统,如大气海洋动力学模型[13]、生物种群模型[14]、神经动力学模型[15]等.文献[16]利用Lyapunov-Krasovskii函数方法对具有时变时滞的随机反应扩散Cohen-Grossberg神经网络的有限时间稳定问题进行了研究;文献[17]对随机反应扩散系统的有限时间稳定问题做了研究,包括分别设计分布式控制器和边界控制器对控制系统进行有限时间镇定、H∞和鲁棒有限时间控制.
受到环境等因素的影响,单一模型并不能很好地刻画真实运行的系统,目前考虑的办法就是建立由有限数量的子系统和相应的切换规则构成的切换系统,如网络控制系统[18]、DC/DC逆变器[19]、飞行控制系统[20]等.对于切换分布参数系统,文献[21]将有限时间有界和有限时间控制问题扩展到切换分布参数系统中,并设计基于事件触发序列的输出反馈控制器使得闭环系统有限时间有界;文献[22]对一类不确定的随机分布参数切换系统的稳定性进行了研究,利用Lyapunov函数方法、随机分析理论中的无穷维伊藤公式、指数鞅不等式等工具,分别得到了系统均方稳定、均方指数稳定以及几乎必然指数稳定的充分条件;文献[23]研究了带马尔可夫跳变的随机反应扩散系统的有限时间稳定问题,并以线性矩阵不等式形式给出了边界控制器存在的充分条件.然而,关于随机分布参数切换系统输入输出有限时间稳定的问题还少有研究,综合以上分析,激发本文对此进行研究.
在本文中,Rn表示n维实向量构成的集合,Rn×m表示全体n×m维实矩阵构成的集合.Iq表示q维单位矩阵.C2,1(Rn×R+;R+)表示实值函数f(z,t):Rn×R+→R+构成的函数空间,且f关于z二阶连续可微,关于t一阶连续可微.W1,2([a,b),Rn)表示绝对连续的n维实值向量函数φ(·,η):[a,b)→Rn构成的函数空间,且φ关于η一阶可微,满足∂φ(·,η)/∂η平方可积.对实矩阵或实向量Π,ΠT表示其转置,trace(Π)表示矩阵Π的迹,Π>0(Π<0)意味着该矩阵正定(负定),记号“*”表示矩阵的对称元素.对随机变量ζ,其数学期望表示为Εζ.
1 问题表述
考虑如下随机分布参数切换系统:
(1)
满足的初边值条件如下:
x(0,η)=0, ∀η∈(0,l),
(2)
x(t,0)=x(t,l)=0,
(3)


(4)
根据文献[24]可知系统(1)运行在t∈[0,t1)上时,即如下方程
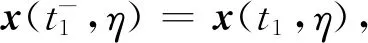
假设1对给定的时间T>0,切换函数σ(t)在有限时间区间[0,T)上的切换次数仅为有限次.
定义1[25]对切换函数σ(t)和时刻t,s满足0≤t≤s,令Nσ(t)(t,s)表示σ(t)在时间区间[t,s)上的切换次数,若存在非负常数N0和正常数τa满足如下关系:
则称N0为抖振界,τa为平均驻留时间(ADT).为简单起见,取N0=0.
考虑如下随机系统:
dz(t)=f(·,t)dt+g(·,t)dw(t),t∈R+.

这里
定义3[27]在零初值条件下,给定m维正定矩阵R和正标量c,T,δ,若对任意满足条件(4)的扰动输入v(t,η),都有

对∀t∈[0,T)成立,则称系统(1)在均方意义下关于(c,T,R,σ(t))输入输出有限时间稳定.
对如下切换随机分布参数控制系统:
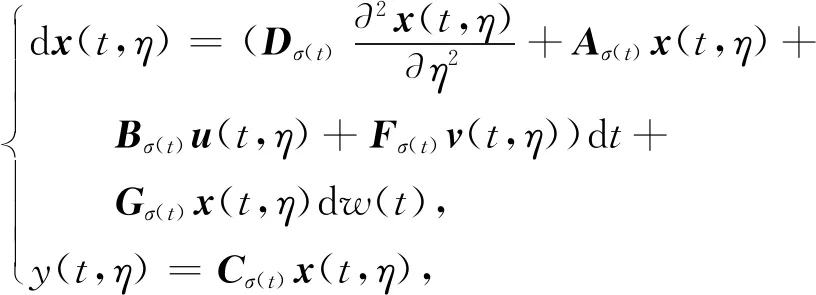
(5)
这里(t,η)∈R+×(0,1),u(t,η)∈Rr是控制输入.系统(5)同样满足初值条件(2)和边值条件(3).
选取状态反馈控制器为
u(t,η)=Kσ(t)x(t,η),
(6)
这里Kσ(t)∈Rr×n是状态反馈增益矩阵.
把控制器的表达式(6)代入系统(5)可得闭环系统

(7)
式中Acσ(t)=Aσ(t)+Bσ(t)Kσ(t).
引理1[28]设β(η)∈W1,2([a,b),Rn),满足β(a)或β(b)=0,Q∈Rn×n且Q>0,则以下不等式成立:

引理2[29]对常数M≥0,p和q,若定义在[0,T)上的实值连续函数g(t)和h(t)满足

则有


2 主要结论
首先给出系统(1)输入输出有限时间稳定的充分条件,然后针对控制系统(5)设计一个状态反馈控制器(6),使得闭环系统(7)输入输出有限时间稳定.


(8)

(9)
0 (10) (11) Pi<λPj, (12) 对任意切换函数σ(t),其平均驻留时间若满足如下不等式: (13) 则系统(1)在均方意义下关于(c,T,R,σ(t))输入输出有限时间稳定. 证明构造Lyapunov-Krasovskii函数: (14) 由分部积分公式和边界条件(3)可得 (15) 注意到x(t,l)=0,那么对式(15)应用引理1,有 (16) 将不等式(16)代入到式(14)可得 (17) 于是有 (18) 对式(8)应用Schur’s补引理可得Θi<0.将Θi<0代入式(18)并两边取期望有 (19) 由无穷维伊藤公式知 (20) 对式(20)两边取期望后,把式(10)和式(19)代入有 (21) 对式(21)应用引理2可得 (22) 对∀t∈[tk,tk+1)成立. (23) 那么,结合定义1并把初值条件(2)代入到式(23)可得 (24) 根据系统(1)的输出方程有 对式(9)应用引理3并结合式(24)可得 (25) 最后,把式(13)代入到式(25)可推得 (26) 证明完毕. (27) (28) 0 (29) (30) Si<λSj. (31) 对任意切换函数σ(t),其平均驻留时间若满足如下不等式 (32) 则在状态反馈控制律(6)下,系统(5)在均方意义下关于(c,T,R,σ(t))输入输出有限时间稳定. (33) 证明完毕. 本节通过两个数值仿真例子来分别验证定理1和定理2结论的有效性. 考虑具有两个模态的系统(1),其相应的系数矩阵和扰动输入为 给定参数c=2.6,T=2,δ=25.2,λ=1.001,R=I,同时取ρ1=8.8,ρ2=0.89,α=0.007 1.通过解定理1中的线性矩阵不等式得可行解如下: 再由式(13)可解得 图1 系统的切换函数σ1(t)Fig.1 Switching function σ1(t) of system 图2 输出轨迹y1(t,η)Fig.2 Output trajectory y1(t,η) 图3 输出轨迹y2(t,η)Fig.3 Output trajectory y2(t,η) 考虑算例1中开环系统(1)所对应的控制系统(5),其相应的输入矩阵为 给定参数c=0.4,T=2,δ=25.2,λ=1.05,R=I,同时取ρ1=10.1,ρ2=0.09,α=0.058 1.通过解定理2中的线性矩阵不等式得可行解如下: 于是可选取状态反馈增益矩阵 图5 系统的切换函数σ2(t)Fig.5 Switching function σ2(t) of system 图6 闭环系统输入输出有限时间稳定Fig.6 Input-output finite-time stability of closed-loop system 图7 开环系统输入输出有限时间稳定Fig.7 Input-output finite-time stability of open-loop system 本文将输入输出有限时间稳定概念引入到了随机分布参数切换系统中,并对随机分布参数切换系统的输入输出稳定性进行了分析.考虑到该系统沿着时间不断切换,通过选择Lyapunov-Krasovskii函数并利用平均驻留时间方法得到了系统输入输出有限时间稳定的充分条件,并设计了一个状态反馈控制器来保证闭环系统输入输出有限时间稳定.此外,解得了控制器的增益Kσ(t).仿真结果表明了该结果的有效性.本文系统的有限时间输入输出镇定问题是基于控制器切换与子系统切换同步的情形即同步切换,此后可以延伸到实际问题中常出现的控制器切换存在滞后的异步切换,这对系统输入输出有限时间的镇定问题提出了挑战,需要进一步讨论异步控制器的设计问题.



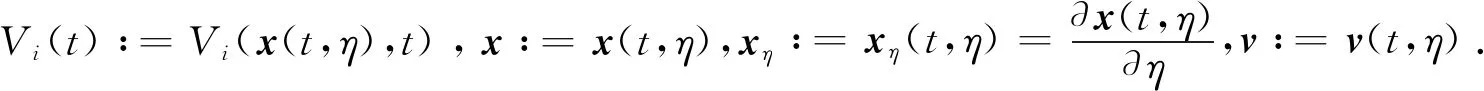









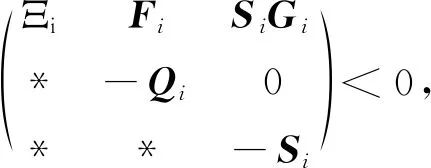



3 仿真算例
3.1 输入输出有限时间稳定





3.2 输入输出有限时间镇定



4 结束语

