基于权重值的竞争深度双Q网络算法
汪晨曦 赵学艳 郭新
0 引言
强化学习(Reinforcement Learning,RL)是由心理学、神经科学以及控制科学等多学科融合而来的一类机器学习方法[1-3],多用于解决序贯决策问题.目前强化学习可以分为基于模型的强化学习(model-based RL)和无模型强化学习(model-free RL)两大类.在无模型强化学习算法中,Q学习(Q-learning)[4]是目前最流行的算法,它使用Q表格有效地构建动作状态对,可直接根据Q值进行动作选择.但在学习训练中,因为Q学习算法包括一个最大化的操作,直接导致对动作值的过于乐观估计,文献[5]证明了该过估计有上限,而文献[6]则证明在特定条件下,该过估计也可能存在下限.
随着人工智能(Artificial Intelligence,AI)、深度学习(Deep Learning,DL)[7]等概念的愈发火热,神经网络已经成为一大研究热点.神经网络可将复杂逻辑的高维数据转换成可靠的低维表示,已在计算机视觉、自然语言处理、推荐系统等方面展示出巨大作用.将深度学习与强化学习结合起来,根据二者不同的特点,可以使得智能体在某些随机环境下获得更为良好的表现.
近年来,深度学习与强化学习相结合(Deep Reinforcement Learning,DRL)的智能体训练方法大放异彩.2013年Mnih等[8]提出的深度Q网络(Deep Q-Network,DQN)算法在Atari 2600部分游戏中大幅超越人类玩家水平,该算法可预估所有策略的价值,取其中最佳策略执行.
最初的DQN算法存在一些缺陷,例如目标值不稳定、样本利用不充分等.针对上述问题,2015年Mnih等[9]提出设立回放经验池和固定目标值以使智能体训练更加稳定:经验回放打破样本前后的关联性,在训练中随机采样,而固定目标值使得反向传播算法更加稳定.但由于估计偏差及噪声作用,该算法有时会高估动作值.
为了解决高估问题,Hasselt等[6]提出DDQN(Double Deep Q-Network)算法,采用双估计器,将动作选择与动作评估分离;文献[10]提出竞争网络结构,将Q网络有效分为价值函数与优势函数两部分,其中价值函数仅仅与状态有关,与动作无关.但Zhang等[11]指出引入双估计器有时会导致低估动作值,提出WDDQ(Weight Double Deep Q-learning)算法,采用权重值的方法对Q值进行调节,仿真结果显示该算法可有效提升训练的稳定性.
本文针对DQN算法中的高估、DDQN算法与竞争网络结构中的低估问题,结合WDDQ算法的权重值方法,提出基于权重值的竞争深度双Q网络算法(Weighted Dueling Double Deep Q-Network,WD3QN),将竞争网络结构与改进的双估计器结合,对动作值有更精准的估计,有效减少误差.通过对Open AI Gym中的经典控制问题CartPole[12]进行研究,实验结果表明,WD3QN算法与已有算法相比有更快的收敛速度和更好的稳定性.
本文的其余部分安排如下:第1节介绍强化学习及其背景知识;第2节给出WD3QN算法设计;第3节给出实验结果与分析;第4节是总结.
1 强化学习及背景知识
1.1 强化学习
在强化学习中,智能体需与外界环境进行交互,找到最优的序列决策,使奖励函数最大化.在一个离散的时间序列t=0,1,2,3,…中,对于每一个时刻t,智能体观察环境状态st∈S,根据当前状态st选择动作at∈A,获得奖励回报rt∈R而后进入下一个状态st+1∈S.马尔可夫决策框架下,使用元组〈S,A,P,R,γ〉表示整个探索过程:S是有限状态集合;A是有限动作集合;状态转移概率P(st+1|st,at)=P[St+1=st+1|St=st,At=at];R(s,a)=Ε[Rt=rt|St=st,At=at]为相应的奖励值;γ∈[0,1],为折扣因子.

若面对离散有限的动作及状态空间,可以使用经典的值迭代算法——Q学习算法.通过学习出一个表格(Q-table),直接表示状态s下每个动作a的未来期望奖励,通过ε-greedy算法采取相应的策略:即以ε概率采取任意可能动作,以1-ε概率采取贪心策略,可避免智能体陷入局部最优;与此同时设置衰减的ε参数,加快中后期智能体的训练速度.Q-learning算法流程如下:
算法1Q-learning
初始化Q,s;
For episode=1,maxepisodedo
在当前状态s下,通过ε-greedy算法,基于Q表格选择动作a;
采取动作a,获取奖励值r及下一状态s′;
a*←argmaxaQ(s′,a),
ζ←r+γQ(s′,a*)-Q(s,a);
Q(s,a)←Q(s,a)+α×ζ,s←s′;
End For
当动作及状态空间很大时,维数灾问题迎面而来,使用表格存下所有的动作状态对显然并不现实.可采用带参数θ的函数近似方法来逼近最优动作价值函数,表达式如下:
Q(s,a;θ)≈Q*(s,a).
(1)
1.2 DQN算法
面对维数颇高的动作及状态空间,经典的Q学习算法显得力不从心,可将表格更新转变为函数近似问题,使用函数值来代替Q表格值.深度神经网络可将复杂逻辑的高维数据转换成可靠的低维表示,有较好的特征提取能力,与Q学习算法结合,即深度Q网络.
在DQN算法中,使用多层神经网络逼近动作价值函数.为提高智能体agent训练时的稳定性,引入两个重要机制:经验回放与固定目标Q值.在训练过程中,当前状态s下选择动作a,获得奖励值r且进入下一状态s′,数据样本(s,a,r,s′)存入经验池中,网络参数θ通过随机梯度下降算法优化,其中目标网络值:
yDQN=r+γmaxa′Q(s′,a′;θ-),
(2)
损失函数如下:
l=(yDQN-Q(s,a;θ))2.
(3)
为避免样本前后关联性对结果的影响,每次随机抽取m个样本数据进行训练.其中θ-代表目标网络参数,θ是当前在线网络参数,二者的网络结构一致,每C步进行赋值:θ-←θ,经验回放与固定目标值可以提升算法的稳定性,获得较好的实验结果,算法流程如下:
算法2DQN算法
1) 初始化Q网络Q(s,a;θ)参数,随机初始化目标网络参数θ-;
2) 初始化经验回放池D及外界环境;
3) 获取初始状态s0,根据ε-greedy算法选择动作a0并记录r0;
4)Fori=1,Ndo
5) 计算目标网络值:yi=ri+γmaxa′Q(si+1,a′;θ-);
6) 计算均方误差损失函数:l=(yi-Q(si,ai;θ))2;
7) 利用随机梯度下降算法更新网络参数;
8) 每过C步,把当前网络参数赋给目标网络:θ-←θ;
9) 将样本数据(si,ai,ri,si+1)存入经验池D;
10)End For
在智能体训练中,DQN算法使用固定Q作为目标值,随机选取经验重放池D中小批量数据样本(s,a,r,s′)进行梯度下降,每C步更新目标网络参数.
2 基于权重值的竞争深度双Q网络算法
2.1 DDQN算法
深度Q网络算法由于选择相应动作时对Q网络值取最大化操作,导致对动作值存在高估问题.深度双Q网络将动作的选择与评估分离,使用在线网络选择动作,而目标网络则对动作进行评估,从而较好地降低过估计.更新方式与DQN类似,公式如下:
yDDQN=r+γQ(s′,argmaxa′Q(s′,a′;θ);θ′).
(4)
与经典深度Q网络算法相比,DDQN算法没有额外增加网络,目标网络与在线网络各司其职,同样每C步对网络赋值:θ′←θ.Hasselt等[6]的实验结果显示,相比于DQN算法,DDQN能有效缓解高估问题,智能体性能有较好提升.
2.2 Dueling网络结构
深度双Q网络通过将动作的选择与评估操作分离,有效降低了过高估计影响.与此同时,Wang等[10]通过优化神经网络结构从而达到优化算法的目的:竞争网络结构将Q网络有效分为价值函数V(s;θ,α)(value function)与优势函数A(s,a;θ,β)(advantage function)两部分,其中价值函数仅与状态有关,与动作无关,如图1[10]所示.
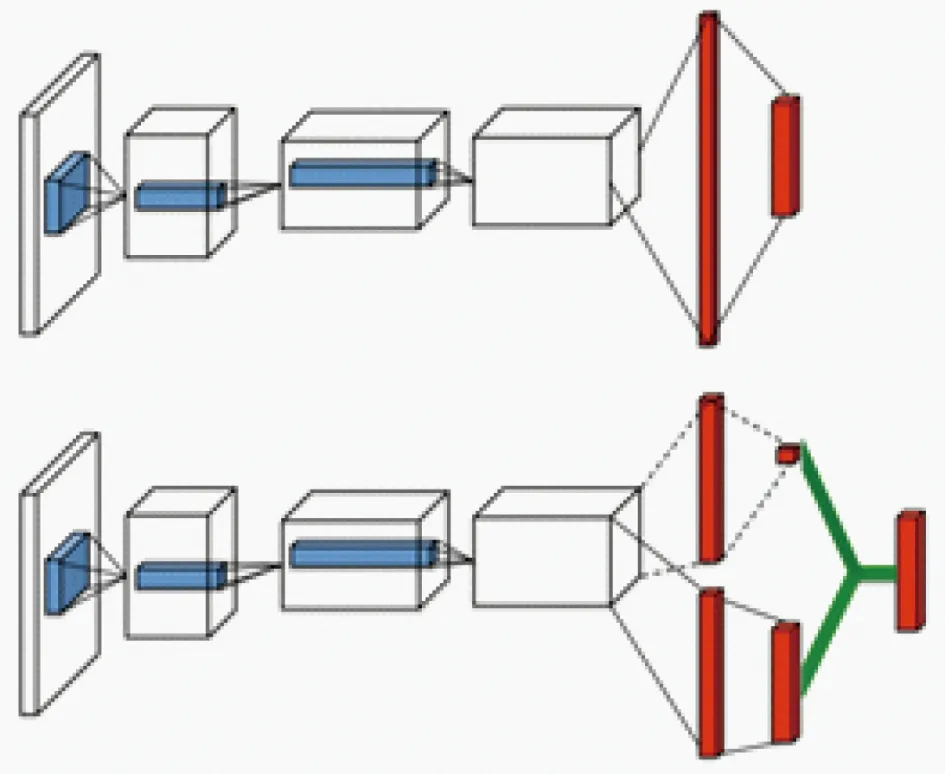
图1 Dueling网络结构[10]Fig.1 Dueling network[10]
公式如下:
Q(s,a;θ,α,β)=V(s;θ,α)+A(s,a;θ,β),
(5)
其中,α,β分别为价值函数与优势函数独有的网络参数,而θ则为公共网络参数.
在竞争网络结构中,优势函数与价值函数作为子网络结构,最终输出值由二者线性组合得到.但在式(5)中,无法直接辨识出价值函数与优势函数各自的作用.为了提高函数可辨识度,实际工程中所使用的方法如下:
Q(s,a;θ,α,β)=V(s;θ,α)+
(6)
对优势函数A(s,a;θ,β)做中心化处理,相比于DQN,仅对Q网络最终输出部分做些许调整,结果证明,竞争网络结构对降低过估计有显著作用,提升智能体性能的同时亦优化了网络的稳定性.
2.3 D3QN算法
将深度双Q网络与竞争网络结构相结合,形成了新的强化学习算法:竞争深度双Q网络算法(Dueling Double Deep Q-Network,D3QN).与DQN相比,D3QN有效缓解了最大化算子带来的过估计影响,算法流程如下:
算法3D3QN算法
1) 初始化Q网络Q(s,a;θ,α,β)参数,初始化目标网络参数θ′,将Q网络的参数值赋给目标网络:θ′←θ,初始化经验池D;
2) For episode=1,maxepisodedo
3) 初始化外界环境,r=0,得到状态s0;
4) Fort=1,maxlengthdo
5) 根据当前状态st,输入在线Q网络中,根据ε-greedy 算法选择当前状态下的动作at;
6) 获取下一状态st+1和即时奖励rt,将样本(st,at,rt,st+1)存入经验池D;
7) 从经验池D中随机抽样(sj,aj,rj,sj+1)m个进行更新;
8) 计算当前Q网络目标值:yj=rj+γQ(sj+1,argmaxa′Q(sj+1,a′;θ,α,β);θ′,α,β);
9) 计算均方误差损失函数:l=(yj-Q(sj,aj;θ,α,β))2;
10) 使用随机梯度下降算法更新优化网络参数;
11) 每经过τ步,有θ′←θ,赋值网络参数;
12) End For
13) End For
2.4 基于权重值的竞争深度双Q网络
深度双Q网络与竞争网络结构,对过估计解决良好,但双Q学习有时也会存在低估问题[11].以上述算法为基础,本文提出WD3QN算法,将双估计器与竞争网络结构结合,Q值基于权重进行调整,综合算法性能.
同样将动作的选择以及评估分离,佐以竞争网络结构,使用Q(s′,a′;θ,α,β)与Q(s′,a′;θ′,α,β)的加权值作目标网络值,计算公式如下:
yWD3QN=r+γ[η×Q(s′,a′;θ,α,β)+
(1-η)×Q(s′,a′;θ′,α,β)],
(7)
式中的η为权值,超参数c在实验中选取,计算公式如下:
η=δ/(c+δ),
(8)
其中δ值计算如下:
δ=|Q(s′,a′;θ′,α,β)-Q(s′,a″;θ′,α,β)|,
(9)
a′,a″分别代表取当前网络值最大与最小动作:
a′=argmaxaQ(s′,a;θ,α,β),
(10)
a″=argminaQ(s′,a;θ,α,β).
(11)
整体算法流程如下:
算法4WD3QN算法
1) 随机初始化Q网络参数θ及目标网络参数θ′;
2) 初始化重放经验池D,初始化智能体环境;
3) For episode=1,maxepisodedo
4) 获取初始状态s0;
5) Fori=1,Tdo
6) 将状态si输入在线Q网络中,根据ε-greedy算法选择动作ai;
7) 获取下一状态si+1和奖励ri,将样本(si,ai,ri,si+1)存入经验池D;
8) 从经验池D中抽取n个样本(sk,ak,rk,sk+1)进行参数更新;
9) a′=argmaxaQ(sk+1,a;θ,α,β),
a″=argminaQ(sk+1,a;θ,α,β);
10) δ=|Q(sk+1,a′;θ′,α,β)-Q(sk+1,a″;θ′,α,β)|,η=δ/(c+δ);
11) 计算目标值:yk=rk+γ[η×Q(sk+1,a′;θ,α,β)+(1-η)×Q(sk+1,a′;θ′,α,β)];
12) 损失函数l=(yk-Q(sk,ak;θ,α,β))2,使用随机梯度下降算法优化网络参数;
13) 每经过τ步,更新目标网络参数:θ′←θ;
14) End For
15) End For
首先进行参数初始化,智能体与环境交互并根据贪心策略选择相应动作,将转移样本(s,a,r,s′)存入经验重放池中.在训练时,随机选取小批量样本数据,根据式(7)计算目标网络值,使用随机梯度下降算法更新相应的网络参数,每τ步对目标网络参数进行赋值.
3 实验分析
3.1 实验平台与参数设置
算法验证环境:Open AI Gym[13],深度学习框架为PyTorch 1.8.1,Python版本3.7,以Gym中经典控制问题CartPole为实验对象,采用DDQN算法,WDDQN算法[14]及D3QN算法作为baseline进行对比,其中经验重放池大小为200 000,minibatch为32,学习率设置0.000 5.WD3QN算法中:以系统状态元组作为输入,第1个全连接层为state_dim×512,而后分别过优势函数与价值函数层(均为512×512),优势函数输出层为512×action_dim,价值函数输出层为512×1,经线性组合得Q(s,a;θ,α,β).D3QN算法与上述基本相同,无基于权重值的双估计器结构;WDDQN算法则无竞争网络结构.训练时选择随机梯度下降算法,贪心策略中初始值为0.1,更新法则如下:ε=max (0.01,ε-10-6),γ=0.99.
3.2 实验结果分析
与传统的监督学习不同,深度强化学习使用自身产生的数据作为训练集,对算法达到稳定快慢以及稳定的持续时间长短进行评估.
首先研究WD3QN算法中超参数c的取值影响,分别取值1,10,100进行训练,图中横坐标episode为训练次数,纵坐标为每次训练的总和回报值,对比结果图2所示.

图2 超参数c=(1,10,100)训练结果Fig.2 Training results with hyperparameter c equals 1 (a),10 (b),and 100(c)
若将以上过程视为训练状态,对智能体每50个episode进行评估,结果如图3所示.
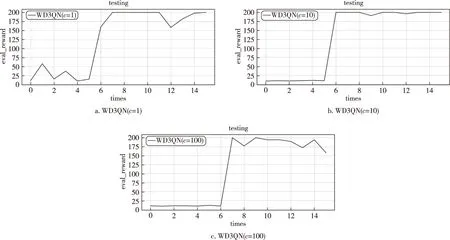
图3 超参数c=(1,10,100)测试结果Fig.3 Testing results with hyperparameter c equals 1 (a),10 (b),and 100(c)
由图3可以看出,算法的收敛性与稳定性在c=10 时优于c=1和100.粗略设置超参数c为常数其实并不准确,在后续研究中,或可以考虑将其设置为自适应参数.下面对比实验中,默认算法超参数c=10.
图4为不同算法(DDQN,D3QN,WDDQN,WD3QN)的训练以及评估效果.

图4 不同算法训练结果Fig.4 Training results of different algorithms
同样对智能体每50个episode进行相应评估,结果如图5所示.

图5 不同算法测试结果Fig.5 Testing results of different algorithms
由图4及图5可以看出,在智能体训练与测试中,WD3QN算法的收敛性与稳定性均明显优于其他三种算法,得益于竞争网络结构与深度双Q网络,缓解了对动作值高估的影响.与此同时,基于权重值的双估计器结构在训练后期(episode>600)减轻对动作值的低估问题,对目标值的估计更加精确.
4 总结
本文提出一种基于权重值的竞争深度双Q网络算法,将深度双Q网络与竞争网络结构结合,引入带权重的双估计器,对目标网络值有更精准的估计,从而有更优的策略选择.通过实验仿真对比,证明该算法的收敛性与稳定性均有效提升.下一步的研究内容即对权重比例c进行探讨,将其设置为自适应超参数;与此同时也可尝试加入循环神经网络结构、图神经网络模型等.

