基于观测器的离散马氏跳变系统的故障估计

王国良 宋歌

0 引言

马氏跳变系统(MJS)是一类特殊的混杂系统,这类系统通常包括两种机制,分别称为时间演化机制和事件驱动机制.前者是状态向量,后者是Markov切换信号,决定了哪个子系统被激活.因此,马氏系统用来描述随机系统的故障估计问题是非常方便的[1-2].当然,在其他问题上也是如此,如H2和H∞控制[3-5]、滤波及估计执行器和传感器故障[6-7]、保成本控制[8]等.

目前,故障估计的方法主要包括基于观测器的方法和基于信号重构的方法.其中,基于观测器的方法不仅能对系统的状态进行估计,而且也能准确地反映故障信息,它主要包含基于自适应观测器[9]、鲁棒观测器[10]以及分布式观测器[11].当系统的参数存在跳变特性时,文献[12-13]考虑了随机通信延迟的马氏系统的故障估计问题,文献[14-16]考虑了执行器和传感器故障的马氏系统综合.文献[17]则考虑切换系统的故障估计问题,设计了一个鲁棒观测器来同时估计系统的状态与故障.该方法虽然很好地处理了基于观测器的切换系统的故障估计问题,但依然有问题需要进一步考虑,比如,用一个随机信号去估计确定性信号.因此,本文提出了一种方法来处理马氏系统与待估计确定性信号之间的问题.

本文采用构建辅助系统的方法研究基于观测器的D-MJSs故障估计问题.主要贡献如下:1)提出一种新的方法来处理故障估计问题,有效解决了随机系统与确定性故障估计之间的矛盾;2)本文方法更具一般性,且保守性更小;3)为了减小不确定TPM带来的影响,使用一些新的放缩手段应用于辅助系统,来处理具有不确定TPM的问题;4)所有条件都以LMI形式给出,并且可以应用于其他系统或问题.

1 准备知识和问题表述

(1)

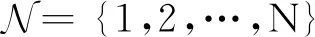
πij=Pr{r(k+1)=j|r(k)=i},

(2)

类似于文献[9,17-18],系统(1)的估计系统描述为

(3)

(4)

(5)

通过qi(k)的定义,进一步得出

Diω(k))1{r(k)=i}1{r(k+1)=j}]=

(6)

Ef(k)+Dω(k)),

(7)

(8)

其估计系统构造为

(9)

eq(k+1)=(ΠT⊗In)[(A-LC)eq(k)+

Eef(k)+Dω(k)],

(10)

Δf(k)+ef(k)-FCeq(k).

(11)

将式(10),(11)合并,得到

(12)

将式(12)简化表示为

(13)

其中

2 主要内容

(14)

I≤P,

(15)

P≤αI,

(16)

其中

P=diag{P1,…,PN,PN+1},

G=diag{G1,…,G1,G2},

观测器增益为

(17)

证明对于系统(13),选取如下形式的Lyapunov函数

(18)

其中P>0.通过计算,可以得到

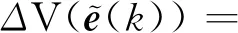
(19)

(20)

根据式(17),得到

(21)

进一步计算得到

(22)

将其计算化简得到

(23)

基于式(23),可以得到

(24)

它等价于

αvT(k)v(k),

(25)

根据式(16),(18)和(25),得

(26)

基于式(26),从0归纳到k,可以得到

⋮

(27)

根据式(15),(16)和(27),可以得到

(28)

进一步简化式(28),有

(29)

证毕.

从定理1以看出,TPM需要准确地给出,但在一些应用中,很难准确得到.因此,当它不确定时,描述为

(30)

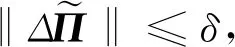
(31)

(32)

(33)

(34)

以及以下任何一种条件

证明为了更简单表示,系统(8)重写为

(35)

‖g(k)‖≤ε‖v‖∞,

(36)

其中ε是正标量.基于式(35),可以得到

⋮

(37)

如果条件

(38)

成立,其中ρ(M)表示矩阵M的谱半径,则可以得到

(39)

关于条件(38),它等价于以下系统的稳定性

(40)

其Lyapunov函数为

(41)

基于文献[19]中的引理2,满足条件是(a)或(b),得到

ΔV(k)=

(42)

式(34)保证其成立.另一方面,条件(34)可以得出

(43)

是渐近稳定的,在相似的Lyapunov函数条件下,计算得出

ΔV(k)=

(44)

类似系统(35)的证明,如果满足此命题中的条件,则可以知道系统(32)和(33)都是ISS.证毕.

接下来,根据系统(32)可以构造一个估计系统

(45)

类似于式(10)和(11),可以根据系统(32)和(45)建立

(46)

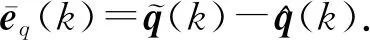
(47)

简化表示为

(48)

其中

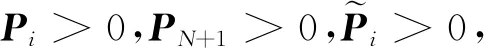
(49)

(50)

以及条件(a)或(b),其中

以及

且矩阵P和G依旧是定理1中的形式,观测器增益仍根据式(17)计算,而控制增益为

(51)

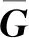
(52)

基于式(51),得到

(53)

经过计算,可得到

(54)

式(50)保证了式(54)成立.系统(48)的Lyapunov函数如下：

(55)

通过计算得出

(56)

(57)

下面的证明与定理1中(24)至(29)的步骤相似,在此省略.证毕.

注3当TPM是不确定时,系统的故障估计问题仍可以通过定理2解决.此外,基于所提出的辅助系统,可以很容易地构造中间估计器.它可以看作是故障估计问题从确定性系统向随机系统的扩展结果.尽管确定性信号f(k)成功估计,但其计算复杂度也是需要考虑的问题.可以看出,所给的LMI的维数较大,同时也包含了许多要求解的变量.其主要原因是所考虑的系统是一个具有N个模态的马氏系统.如何进一步降低复杂性是一个必要且重要的问题,这将是我们今后要做的工作.本文所提出的方法更具有一般性,而且可以扩展到其他问题.第一,因为r(k)是一个随机过程,所以一些确定性系统的故障估计问题可以作为本文的一个特殊情形；第二,它可以用来处理半马尔可夫跳变系统,尽管半马尔可夫跳变过程更具有一般性.

3 仿真研究

考虑系统(1)的模型[17,20],参数为

给定α=65,根据定理1,可得观测器增益为

和

F1=0.329 0,F2=0.505 4,

F3=0.113 7,F4=-0.187 8.

不失一般性,故障信号f(k)如下所示:

图1 状态曲线ζ(k)和Fig.1 State curves of ζ(k) and

图2 模态r(k)的仿真Fig.2 Simulation result of modal r(k)

图3 误差曲线ex(k)Fig.3 Error curves for ex(k)

图4 故障f(k),估计和估计误差ef(k)Fig.4 Failure f(k),estimation and estimation error ef(k)

当Π不确定时,可以通过定理2来研究类似的问题.不失去一般性,基于式(30),假设

与此同时,令δ=0.23,ζ=3.5.根据定理2,控制器增益计算为

观测器增益为

和

F1=-0.050 0,F2=-0.035 8,

F3=0.010 7,F4=0.010 7.

最后,为进一步比较,并证明本文提出的方法的优点,不失一般性,假设

其中θ≥0表示为扰动.一方面,当θ=0时,从定理1可以得出α的最小可行解αmin=3.2,而文献[17]中相应的αmin=10.99且更大.即使对上述不确定的TPM,定理2得到的最小可行解αmin=3.8,仍然小于文献[17],但大于αmin=3.2.由此可见,本文方法的保守性较小.另一方面,当α=81时,基于定理2的θ的最大可行解θmax=1.91,大于文献[18]中得到的θmax=1.58;同时,定理2的相应最大可行解θmax=1.67.与前一种情况结果相似,可知本文方法保守性更小.

4 结束语

本文采用辅助系统方法研究了D-MJSs的故障估计问题,可以很好地解决随机系统与确定性故障之间的矛盾.通过对随机变量求取期望,构造确定性中间变量,并利用中间估计器来同时估计状态与故障.通过放缩手段研究了TPM的其他情况.通过仿真算例验证了结果的实用性与优势.仍然有以下问题需要考虑:第一,r(k)在中间变量式(4)中很重要,当其无法得到时,如何考虑类似问题是必要且更贴合实际的;第二,应进一步降低计算复杂度和保守性,尤其是系统模态大幅增加后;第三,当Π由式(32)表示,但δ未知时,如何进行有效估计是很有必要的.本文的结论同样适用于其他系统或问题,例如非线性系统、多智能体系统和滤波器设计.