噪声采样区间下具有随机短时滞的网络化系统镇定研究
胡志佩 苏永康 邓飞其
0 引言
近年来,随着数字硬件技术的飞速发展,采样控制方法在网络化系统的镇定问题中得到了广泛的研究[1-9].然而,由于通信网络的容量有限,采样数据在传输过程中可能诱导出网络时延,从而对被控系统产生重要影响,并可能导致系统故障、不稳定或性能下降[10-12].因此,研究具有时变时滞的网络化控制系统的镇定问题具有重要意义.例如,在考虑时变短时滞的情况下,文献[13]用鲁棒控制方法研究了一类网络化采样数据系统的稳定性问题.更多关于时变短时滞下网络化控制系统的稳定性问题研究见文献[14-16].注意到在许多情况下,网络诱导时滞是随机的[17],因此,已有一些文献研究了时变采样间隔和随机时变时滞双重影响下采样数据系统的控制问题,可参见文献[18-19]以及其中的参考文献.
需要注意的是,在上述文献中,所考虑的网络化采样数据系统的采样间隔(周期性和非周期性)通常被假定为有界的和确定性的.然而,在工程实践中,由于不良的物理约束(例如时钟误差漂移、信号传输设备的性能退化和采样器的随机故障),网络化控制系统的采样间隔通常以随机方式发生[20].换言之,实际采样间隔可能受到噪声干扰,并基于某个概率分布在理想采样周期周围随机波动.近年来,已有一些关于噪声采样间隔下采样数据系统控制的研究成果.例如:对于具有噪声采样间隔的采样数据系统,文献[21]和[22]分别研究了单一控制输入的镇定问题和多控制输入的量化/饱和控制问题;文献[23]通过假设采样误差遵循分类分布来设计同步控制器.需要指出的是,在大多数现有的关于具有随机时滞的采样数据控制系统的研究中,很少是基于噪声采样间隔下进行的.因此,本文的第一个动机是建立一个统一的框架使得噪声采样区间下具有随机时滞的采样数据系统得以镇定.
针对采样数据系统的镇定问题,已有文献主要采用输入延迟方法[24]、离散时间方法[25]和脉冲建模方法[26]对其进行建模和分析.例如:文献[27]采用输入延迟方法研究了具有常数时滞的多智能体采样数据系统的领导者和跟随者一致性问题;文献[16]利用离散时间方法,研究了一类具有短时变时滞的采样数据系统的模型预测控制问题.但是,到目前为止,很少有文献利用离散时间方法来研究具有随机时滞的网络化系统镇定问题,特别是在实际采样间隔受噪声扰动的情况下.利用离散时间方法对最初的系统建模后,等价的离散模型的系统矩阵由于包含采样误差和采样误差与随机时滞之差这两个随机变量而具有高度非线性和双重随机性.找到有效的方法计算包括系统矩阵在内的三个矩阵乘积的数学期望值,对于控制器的设计至关重要.因此,本文的第二个动机是解决离散时间方法建模后控制器设计所面临的困难.
基于上述分析,本文致力于研究噪声采样区间下具有随机时滞的网络化系统的镇定问题.主要贡献可总结如下:1)研究了一类具有随机时滞的网络化采样数据系统的新的镇定问题.其中,实际采样间隔由于受到噪声扰动的影响,它以某种概率分布围绕着理想采样周期随机波动.文献[13-16]可以看成是本文的特例.2)利用离散时间方法建模后,等效的离散时间系统具有高度非线性和双重随机性,在期望运算中采用汇合范德蒙矩阵法和克罗内克积运算解决了控制器设计难点.3)考虑的采样误差可以是连续或离散的随机变量.本文在仿真中给出了两种特殊情况,包括服从均匀分布的连续采样误差和一类离散采样误差.
1 问题构建及系统建模
考虑以下受噪声采样间隔和随机时变时滞影响的网络控制系统:
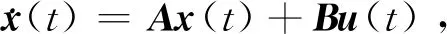
(1)
其中,状态向量x(t)∈Rn和控制输入u(t)∈Rm,A和B是具有适当维数的常数矩阵,x(0)是系统(1)的初始值.
系统(1)是非周期采样的并且采样区间hk由两个部分组成,hk=h+εk,其中常数h表示理想周期采样间隔,随机变量εk表示不可预测的环境导致的采样误差.随机变量εk的概率密度函数(概率质量函数)记为f(ε).
注1在本文中,采样误差εk可以是连续的或离散的随机变量.假设概率密度函数或概率质量函数是给定的.在仿真部分中除了讨论连续采样误差的情况外,还讨论了服从离散概率分布的采样误差.
本文给出了以下两个假设:
假设1时滞τk=τsc(k)+τca(k),其中0≤τk 注2文献[28]利用时滞分析方法来减少生产停机时间,并可估计故障时滞的概率密度函数;文献[29]所考虑的时滞遵循指数分布;文献[30]基于互联网的机器人遥操作系统的时滞服从平行转移伽玛分布.在本文中,随机延迟τk的概率分布是一般的,其中,文献[28-30]中的概率分布是本文的特例. 假设2随机变量εk和随机时滞τk是相互独立的. 对被控对象(1)进行采样周期为hk的采样后,具有零阶保持器的控制输入u(t)为 (2) (3) 注3基于假设2,可以用卷积公式计算随机变量εk-τk的概率密度函数(概率质量函数).在本文,设σk=εk-τk,并将随机变量σk的概率密度函数(概率质量函数)记为f(σ). 需要注意的是,随机变量εk和随机变量σk的存在给期望的计算带来了困难. 因此,系统(3)可以重新表示为 xk+1=(I+H1(εk)+J(σk))xk+ (H2(εk)-J(σk))xk-1. (4) 本文的目的是设计一个镇定控制器,使随机增广系统(4)是随机稳定的.更具体地说,如果对任何初始状态y(0)∈R2n,成立,那么随机增广系统(4)是随机稳定的. 本节考虑噪声采样区间下具有随机时滞的线性网络化系统的镇定问题.为证明本文的主要结论,首先给出以下引理. 引理1[22]矩阵A∈Rn×n具有特征值λ1,λ2,…,λl及它们的重数n1,n2,…,nl,其中n1+n2+…+nl=n.那么可以得到 (5) 其中: π(s)=[eλ1sseλ1s…sn1-1eλ1s… eλlsseλls …snl-1eλls], 而Va是文献[22]中的汇合范德蒙矩阵. 根据引理1,从(5)可以得出 (6) (7) 引理2对于存在一个矩阵Ug使得 (8) 证明对于任意ξ≠0, ξT ξT 即存在一个矩阵Ug使得(8)成立.证毕. (9) 以下的定理用于设计增广系统(4)的镇定控制器. 定理1给定正参数α,β,γ,κ,如果存在矩阵X>0,Z>0和Y,使下列不等式成立: (10) 其中: 而Γ1,Γ2则分别定义在式(6)和(7)中,那么离散时间随机系统(4)是随机稳定的.另外,如果不等式(10)是可解的,控制器增益参数为K=YX-1. ΔV(yk)={V(yk+1)|yk}-V(yk). (11) 然后可以通过(4)和(11)得到 (12) 其中,Λ1=I+H1(εk)+J(σk), Λ2=H2(εk)-J(σk). 通过引理1和引理2,通过(5)和(8)可以得到 (13) 运用同样的方法,通过(5)和(9)可以得到 (14) 对于任意α>0,通过(13)和(14)可以得到下列不等式 (15) 根据(6)、(7)以及(15),可以得到 (16) 同样地,对于任意β>0,通过(13)和(14),可以得到 (17) 根据式(13)、(14)以及(17),可以得到 (18) (19) 而在任意κ>0的情况下,下列不等式成立: (20) 结合(19)、(20),根据(6)、(7)以及(13)、(14),可以得到 (21) 结合(16)、(18)以及(21),(12)可以重新表示为 (22) 其中: (23) 成立,其中: Ξ2=PΓ1BK-PΓ2BK, 算例1考虑一个由(1)描述的连续时间线性系统,系统矩阵如下: A=-0.50.80.40-0.50.12000.1, 根据引理1,可以得到矩阵A的特征值分别为λ1=-0.5和λ2=0.1,其重数分别为n1=2和n2=1.然后,可以得到汇合范德蒙矩阵 选定理想周期采样间隔为h=0.25.假设采样误差服从-0.03到0.03的均匀分布,时滞服从0到0.07的均匀分布.因此,可以得到 矩阵Ug和Uh可通过计算得出: 假设α=β=γ=κ=1.利用MATLAB 2015b上的LMI工具箱求解不等式(10),得到如下可行解: 根据定理1,设计的控制器增益为 图1 无控制输入时系统的状态轨迹Fig.1 State trajectories of system without control inputs 图2 服从均匀分布的时滞Fig.2 Time-delay obeying uniform distribution 图3 服从均匀分布的采样误差(上)和带有控制器的闭环系统(下)的状态轨迹Fig.3 Sampling errors obeying uniform distribution (up) and state trajectories of closed loop system with controller (bottom) 算例2考虑以下系统模型[32]: 选定理想周期采样间隔为h=0.5.假设采样误差是一个具有概率质量函数的离散随机变量,且其概率质量函数为 (24) 设ρ=0.4.假设时滞服从0到0.3的均匀分布,α=β=γ=κ=1.通过求解线性矩阵不等式(10),可以得到 根据定理1,设计的控制器增益为 通过两个仿真算例得出的结果,可以看出,本文的设计方法是有效的. 本文研究了噪声采样区间下具有随机时滞的网络化系统镇定问题.首先,利用离散时间方法建立了一个等效随机系统模型,但其系统矩阵具有高阶非线性和双重随机性.然后,利用汇合范德蒙矩阵方法和克罗内克积运算,计算了包括离散时间系统矩阵在内的三个矩阵乘积的数学期望,并设计出了镇定控制器.最后,通过两个仿真算例验证了所设计方法的有效性.


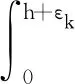



2 主要结果


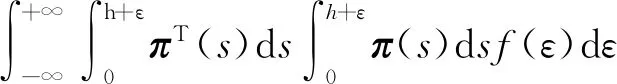



3 仿真算例





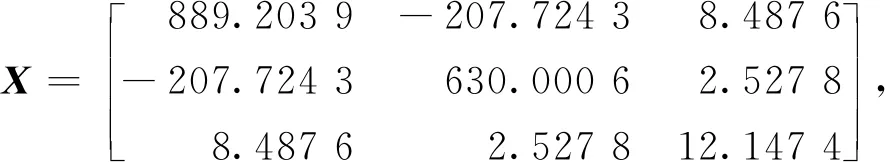
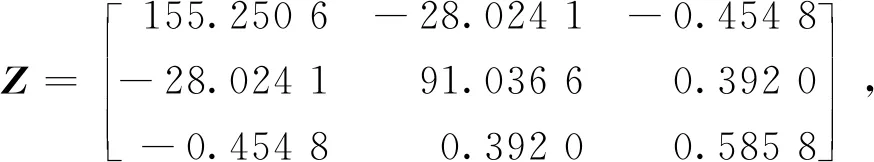




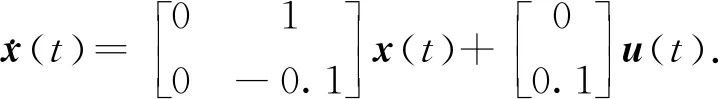
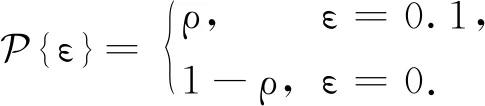

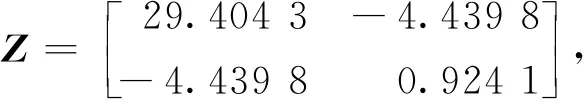


4 结语

