Cycle lengths in graphs of chromatic number five and six

Huo Qingyi

School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China

Abstract: A problem was proposed by Moore and West to determine whether every (k+1)-critical non-complete graph has a cycle of length 2 modulo k. We prove a stronger result that for k=4, 5, every (k+1)-critical non-complete graph contains cycles of all lengths modulo k.

Keywords: cycle length; chromatic number; minimum degree; breadth-first search tree

1 Introduction

The problem of deciding whether a given graph contains cycles of all lengths modulo a positive integerkshows up in many literature (see Refs.[1-8]). Recently, Moore and West[9]asked whether every (k+1)-critical non-complete graph has a cycle of length 2 modulok. Here, a graph isk-critical if it has chromatic numberkbut deleting any edge will decrease the chromatic number.Very recently, Gao et al.[10]partially answered this question by showing the following theorem.

Theorem 1.1Fork≥6, every (k+1)-critical non-complete graph contains cycles of all lengths modulok.

However, methods in Ref.[10] do not work fork<6. In this note, we give a new method and prove that the conclusion of Theorem 1.1 also holds fork=4, 5.

Theorem 1.2Fork=4, 5, every (k+1)-critical non-complete graph contains cycles of all lengths modulok.

Thus, combined with the Theorems 1.1 and 1.2, we completely give an affirmative answer to the question of Moore and West.

The rest of the paper is organized as follows. In Section 2, we introduce the notation. In Section 3, we give a key lemma. In Section 4, we consider graphs of chromatic number five and prove Theorem 1.2 for the casek=4. In Section 5, we consider graphs of chromatic number six and prove Theorem 1.2 for the casek=5.

2 Notation

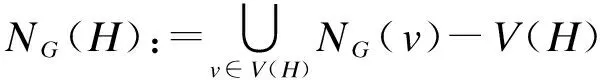
A cycle or a path is said to be odd (resp. even) if its length is odd (resp. even). Given a cycleCand an orientation ofC, for two verticesxandyinC, letC[x,y] denote the path onCfromxtoyin the direction, includingxandy. LetC[x,y):=C[x,y]-y,C(x,y]:=C[x,y]-x, andC(x,y):=C[x,y]-{x,y}. We use the similar notation to a pathP.

Letuandvbe two vertices of a graph. If there are three internally disjoint paths betweenuandv, then we call such a graph as the theta graph. Note that any theta graph contains an even cycle.

A vertexvof a graphGis a cut-vertex ofGifG-vcontains more components thanG.A blockBinGis a maximal connected subgraph ofGsuch that there exists no cut-vertex ofB. So a block is an isolated vertex, an edge or a 2-connected graph. An end-block inGis a block inGcontaining at most one cut-vertex ofG. IfDis an end-block ofGand a vertexxis the only cut-vertex ofGwithx∈V(D), then we say thatDis an end-block with cut-vertexx.

LetTbe a tree, and fix a vertexras its root. Letvbe a vertex ofT. The parent ofvis the vertex adjacent tovon the path fromvtor. An ascendant ofvis any vertex which is either the parent ofvor is recursively the ascendant of the parent ofv. A child ofvis a vertex of whichvis the parent. A descendant ofvis any vertex which is either the child ofvor is recursively the descendant of any of the children ofv. LetYbe a subset ofV(T). We say a vertexxis the descendant ofYifxis the descendant of some vertex inY. Leta,bbe two vertices ofT. DenoteTa,bthe unique path betweenaandbinT.

3 Key lemma

LetGbe a 2-connected graph and letCandDbe two cycles inG.We say that (C,D) is an opposite pair inG, ifCis odd andDis even satisfying thatCandDare edge-disjoint and share at most one common vertex.

Lemma 3.1LetGbe a 2-connected graph of minimum degree at least 4. Let (C,D) be an opposite pair inG. ThenGcontains cycles of all lengths modulo 4.

ProofSuppose to the contrary thatGdoes not contain cycles of all lengths modulo 4. SinceGis 2-connected and |V(C)∩V(D)|≤1, there exist two vertex-disjoint pathsP,QbetweenCandDsatisfying (V(C)∩V(D))-V(Q)=Ø(1)We remark that (i) if V(C)∩V(D)=Ø, then P and Q are vertex-disjoint, (ii) if C and D share one common vertex, then V(Q)=V(C)∩V(D).. We take such an opposite pair (C,D), pathsPandQas the following manner:

① |E(P)| is as large as possible;

② |E(Q)| is as large as possible subject to ①.

Letpandqbe the endpoints ofPandQinD, respectively.

Claim 1Every even cycle in the block ofG-(V(C∪P∪Q)-{p,q}) includingDcontains bothpandq.In particular, every theta graph in the block includes bothpandq.

Proof of Claim 1LetHbe the block of

G-(V(C∪P∪Q)-{p,q})

includingD. LetD′ be an even cycle inHother thanD. Suppose thatp∉V(D′). SinceHis 2-connected, there are two vertex-disjoint pathsL1,L2from {p,q} toD′ inH. We may assume thatL1linkspandD′. Note thatL1has a length at least 1 and (C,D′) is an opposite pair. ThenP∪L1andQ∪L2are two internally disjoint paths betweenCandD′ such thatP∪L1is longer thanP, a contradiction. Therefore,p∈V(D′).

Suppose thatq∉V(D′). SinceHis 2-connected, there is a pathL3fromqtoD′ internally disjoint fromV(D′) inH. Note thatL3has a length at least 1 and (C,D′) is an opposite pair. ThenPandQ∪L3are two internally disjoint paths betweenCandD′ such thatQ∪L3is longer thanQ, a contradiction. Therefore,q∈V(D′). Since every theta graph contains an even cycle, every theta graph inHincludes bothpandq. This completes the proof of Claim 1.

SinceDis an even cycle, we partitionV(D) into the setsAandBalternatively alongD. By symmetry betweenAandB, we may assume thatp∈A.

Claim 2For anyb∈B-{q}, there is no path frombtoC∪P∪Q-{p,q} internally disjoint fromC∪D∪P∪Q.

Proof of Claim 2Suppose to the contrary that there is a pathRfrombtox∈V(C∪P∪Q)-{p,q} internally disjoint fromC∪D∪P∪Q. By symmetry, we may assume thatb∈D(p,q).

Assume that |E(D)|≡0 mod 4. AsCis an odd cycle, there is an even pathX1and an odd pathY1betweenpandqinC∪P∪Q. Ifq∈B, then both |E(D[p,q])| and |E(D[q,p])| are odd, and furthermore, since their sum is 0 modulo 4, they differ by 2 modulo 4. ThenX1∪D[p,q],X1∪D[q,p],Y1∪D[p,q] andY1∪D[q,p] are 4 cycles of different lengths modulo 4, a contradiction. Therefore, we have thatq∈A.

Suppose thatx∈V(P)-{p}. SinceCis an odd cycle, there is an even pathX2and an odd pathY2betweenbandqinC∪P∪Q∪R. However, since both |E(D[b,q])| and |E(D[q,b])| are odd and differ by 2 modulo 4,X2∪D[b,q],X2∪D[q,b],Y2∪D[b,q] andY2∪D[q,b] are 4 cycles of different lengths modulo 4, a contradiction. Thus,xis not contained inV(P)-{p}.

Suppose thatx∈V(C∪Q)-(V(P)∪{q}). Then there is an even pathX3and an odd pathY3betweenbandpinC∪P∪Q∪R. However, since both |E(D[b,p])| and |E(D[p,b])| are odd and differ by 2 modulo 4,X3∪D[b,p],X3∪D[p,b],Y3∪D[b,p] andY3∪D[p,b] are 4 cycles of different lengths modulo 4, a contradiction. Thus,xis not contained inV(C∪Q)-(V(P)∪{q}).

Therefore, |E(D)|≡2 mod 4. AsCis an odd cycle, there is an even pathX4and an odd pathY4betweenpandqinC∪P∪Q. Ifq∈A, then both |E(D[p,q])| and |E(D[q,p])| are even, and furthermore, since their sum is 2 modulo 4, they differ by 2 modulo 4. ThenX4∪D[p,q],X4∪D[q,p],Y4∪D[p,q] andY4∪D[q,p] are 4 cycles of different lengths modulo 4, a contradiction. Therefore, we have thatq∈B.

Suppose thatx∈V(C∪P)-(V(Q)∪{p}). SinceCis an odd cycle, there is an even pathX5betweenbandqand an odd pathY5betweenbandqinC∪P∪Q∪R. However, since both |E(D[b,q])| and |E(D[q,b])| are even and differ by 2 modulo 4,X5∪D[b,q],X5∪D[q,b],Y5∪D[b,q] andY5∪D[q,b] are 4 cycles of different lengths modulo 4, a contradiction. Thus,xis not contained inV(C∪P)-(V(Q)∪{p}).

Suppose thatx∈V(Q) -{q}. SinceGis a 2-connected graph of minimum degree at least 4, there exists a pathTfrombtoy∈V(C∪D∪P∪Q∪R)-{b} internally disjoint fromC∪D∪P∪Q∪R. As the same reason forx,yis not contained inV(C∪P)-(V(Q)∪{p}). Thereforey∈V(Q∪D∪R)-{b}.

Ify∈V(R∪Q∪D(b,p))-{b}, thenD[b,p)∪R∪T∪Qcontains a theta graph. It follows that there is an evenD1cycle inG-(C∪P-Q). Note that (C,D1) is an opposite pair inG. It is easy to see that there are two internally disjoint pathsP′ andQ′ betweenCandD′ satisfying thatP′ containsPand is longer thanPandQ′⊆Q∪D(b,q]∪R, a contradiction. Thus,yis not contained inV(R∪Q∪D(b,p))-{b}.

Suppose thaty∈V(D[p,b)). SinceT∪D[y,b] does not containqandD[b,q]∪R∪Q[x,q] does not containp, by the choice of opposite pairs, we have thatT∪D[y,b] andD[b,q]∪R∪Q[x,q] are both odd cycles. SinceCis an odd cycle, there is an odd pathX′ and an even pathY′ betweenyandxinC∪P∪Q∪D[p,y]. Note that the lengths ofX′ andY′ differ by 1 modulo 4, the lengths ofTandD[y,b] differ by 1 modulo 4 and the lengths ofD[b,q]∪Q[x,q] andRdiffer by 1 modulo 4. Then the set

{L1∪L2∪L3|L1∈{X′,Y′},

L2∈{T,D[y,b]},

L3∈{D[b,q]∪Q[x,q],R}}

contains cycles of all lengths modulo 4, a contradiction. Thus,yis not contained inV(D[p,b)).

This completes the proof of Claim 2.

Letzbe a vertex inB-{q}. By symmetry between two orientations ofC, we may assume thatz∈V(D(p,q)). Since the degree ofzis at least 4 inGandGis 2-connected, there is a pathZfromztoC∪D∪P∪Q-{z} internally disjoint fromC∪D∪P∪Q. By Claim 2, the endpoint ofZother thanzis contained inD-{z}. Letrbe the endpoint ofZother thanz. Since the degree ofzis at least 4 inGandGis 2-connected, there is a pathSfromztos∈V(C∪D∪P∪Q∪Z)- {z} internally disjoint fromC∪D∪P∪Q∪Z. By Claim 2,sis contained inV(D∪Z)-{z}.

Suppose thats∈V(Z)-{z}.

Ifr∈V(D(z,p)), thenD[z,r]∪Z∪Sis a theta graph not containingp, contradicting Claim 1.

Ifr∈V(D[p,z)), thenD[r,z]∪Z∪Sis a theta graph not containingq, contradicting Claim 1.

Thus,sis not contained inV(Z)-{z}.

Suppose thats∈V(D)-{z,r}. By symmetry betweenrands, we may assume thats∈V(D(r,z)).

Ifr∈V(D(q,z)), thenD[r,z]∪Z∪Sis a theta graph not containingq, contradicting Claim 1.

Ifr∈V(D(z,q]) ands∈V(D(r,p)), thenD[z,s]∪Z∪Sis a theta graph not containingp, contradicting Claim 1.

Thereforer∈V(D(z,q]) ands∈V(D[p,z)). SinceS∪D[s,z] does not containqandD[z,r]∪Zdoes not containp, by Claim 1, we have thatS∪D[s,z] andD[z,r]∪Zare both odd cycles. SinceCis an odd cycle, there is an odd pathX″ and an even pathY″ betweensandrinC∪P∪Q∪D[p,s]∪D[r,q]. Note that the lengths ofX″ andY″ differ by 1 modulo 4, the lengths ofSandD[s,z] differ by 1 modulo 4 and the lengths ofD[z,r] andZdiffer by 1 modulo 4.Then the set {L1∪L2∪L3|L1∈{X″,Y″},L2∈{S,D[s,z]},L3∈{D[z,r],Z}} contains cycles of all lengths modulo 4, a contradiction.

This completes the proof of Lemma 3.1.

4 Graphs of chromatic number five

In this section, we prove the following theorem on 2-connected graphs of the minimum degree at least four, from which Theorem 1.2 can be inferred as a corollary for the casek=4.

Theorem 4.1Every 2-connected non-bipartite graph of the minimum degree at least 4 contains cycles of all lengths modulo 4, except that it is the complete graph of five vertices.

ProofLetGbe a 2-connected non-bipartite graph of the minimum degree at least 4. Assume thatGis not aK5and does not contain cycles of all lengths modulo 4. LetC:=v0v1…v2lv0be an odd cycle inGsuch that |V(C)| is minimum, where the indices are taken under the additive group2l+1. Note thatCis induced. LetH:=G-V(C). By Lemma 3.1, there is no opposite pairs inG, henceHdoes not contain an even cycle. It follows that every block ofHis either an odd cycle, an edge or an isolated vertex.

ClaimGdoes not contain a triangle.

Proof of ClaimSuppose thatGcontains a triangle. ThenCis a triangle. LetH1be a component ofH. Since the minimum degree ofGis at least 4,H1has at least two vertices. Suppose thatH1contains an odd cycleC1.

IfH1is not 2-connected, then there exists an end-blockB1ofH1with cut-vertexb1such that

(V(B1)-{b1})∩V(C1)=Ø.

AsB1is either an odd cycle or an edge, there existsw∈V(B1)-{b1} such thatwhas at least two neighbors onC. SinceCis an odd cycle,G[C∪{w}] contains an even cycleD1. ThenC1andD1form an opposite pair inG, a contradiction.

Therefore,H1is 2-connected, that isH1is an induced odd cycle, we denoteH1:=u0u1…u2hu0, where the indices are taken under the additive group2h+1. Since the minimum degree ofGis at least 4,u0andu2have at least two neighbors onC. Without loss of generality, we may assume thatu0is adjacent tov0andv1andu2is adjacent tov0. ThenC,u0v0v2v1u0,u0u1u2v0v1u0andu0u1u2v0v2v1u0are cycles of lengths 3, 4, 5 and 6, respectively, a contradiction.

Therefore, every component ofHdoes not contain an odd cycle, that is, every component ofHis a tree.

If |V(H1)|=2, thenG[C∪H1] is aK5. Suppose that there is another componentH2≠H1ofH.SinceGis 2-connected, there are two disjoint pathsL1andL2fromH2toCinternally disjoint fromCinG[H2∪C]. Without loss of generality, we may assume thatV(Li)∩V(C)={vi} fori=1, 2. ConcatenatingL1,L2and a path inH2, there exists a pathLfromv1tov2internally disjoint fromCinG[H2∪C]. As there are paths of lengths 1, 2, 3 and 4 fromv1tov2inG[H1∪C], we could easily obtain 4 cycles of consecutive lengths, a contradiction. Therefore,H=H1. It follows thatG=G[C∪H1], a contradiction.

Therefore |V(H1)|≥3. For any two leavesx,yofH1, letTbe the fixed path betweenxandyinH1.Since the minimum degree ofGis at least 4,xandyhave at least three neighbors onC.Without loss of generality, we may assume thatxis adjacent tov0andv1andyis adjacent tov0. IfTis even, thenCandv0yTxv0form an opposite pair, a contradiction. ThereforeTis odd. Suppose that there exist three leavesx,yandzinH1. LetTx,y,Ty,zandTz,xbe the fixed paths betweenxandy,yandzandzandxinH1, respectively. Note that all of them are odd. However, their sum is even, a contradiction. Therefore,H1is a path. LetH1:=z0z1z2…znfor somen≥2. Since the minimum degree ofGis at least 4,z0is adjacent to all vertices ofCandz2is adjacent to at least 2 vertices ofC. Without loss of generality, we may assume thatz2is adjacent tov0andv1. ThenC,z0v0v2v1z0,z0z1z2v0v1z0andz0z1z2v0v2v1z0are cycles of lengths 3, 4, 5 and 6, respectively, a contradiction.

This completes the proof of Claim.

By Claim,Gdoes not contain a triangle. Suppose that there is a vertexuof degree at most one inH. Since the minimum degree ofGis at least 4,uhas at least three neighbors onC. SinceCis odd, there exist two distinct neighborsvi,vjofuonCsuch that the odd path betweenviandvjonChas no internal vertices which are the neighbors ofuinG. LetQo,Qebe the odd and even paths betweenviandvjinCrespectively. LetC′:=uvi∪Qo∪vju. Note thatC′ is an odd cycle. By the choice ofC, we have that |E(C′)|≥|E(C)|. This forces that |E(Qe)|=2 anduis adjacent to all vertices ofV(Qe). It follows that there is a triangle inG, a contradiction. Therefore, the minimum degree ofHis at least 2.

Suppose thatHhas more than one component. LetW1andW2be two components ofH. Since the degree of any vertex inW1is at least 2, we have thatW1contains an odd cycleC2. SinceGis 2-connected andCis an odd cycle, there is an even cycleD2inG[V(C)∪W2]. Thus,C2andD2form an opposite pair, a contradiction. Therefore,His connected.

Note that the minimum degree ofHis at least 2 and every block ofHis either an odd cycle, an edge or an isolated vertex. There is a vertextofHwhich has at least two neighbors onC. SinceCis odd, there exist two distinct neighborsvi,vjoftonCsuch that the odd path betweenviandvjonChas no internal vertices which are the neighbors oftinG. LetQ′o,Q′ebe the odd and even paths betweenviandvjinCrespectively. LetC″:=tvi∪Q′o∪vjt. Note thatC″ is an odd cycle. By the choice ofC, we have that |E(C″)|≥|E(C)|. This fores that |E(Q′e)|=2. Without loss of generality, we may assume thati=j+2. Letsbe the neighbor ofvj+l+1inH. Note thatChas length at least five. If follows thatvj+l+1≠vi,vj. SinceHis connected, there is a pathLbetweentandsinH. ThenC[vj+2,vj+l+1]∪vj+l+1s∪L∪tvj+2,C[vj+l+1,vj]∪vjt∪L∪svj+l+1,C[vj,vj+l+1]∪vj+l+1s∪L∪tvj,C[vj+l+1,vj+2]∪vj+2t∪L∪svj+l+1are 4 cycles of consecutive lengths, a contradiction. This completes the proof of Theorem 4.1.

We remark that Theorem 4.1 is best possible by the following examples. For any positive integert, letPt:=v0v1…v2t+1andQt:=u0u1…u2t+1be two vertex-disjoint paths. LetHtbe the graph obtained fromPt∪Qtby adding edges in {v2iu2i+1,u2iv2i+1,u0v0,u2t+1v2t+1|i=0, 1, …,t}. We see thatHtis a 2-connected non-bipartite graph of the minimum degree 3 without cycles of length 1 modulo 4.

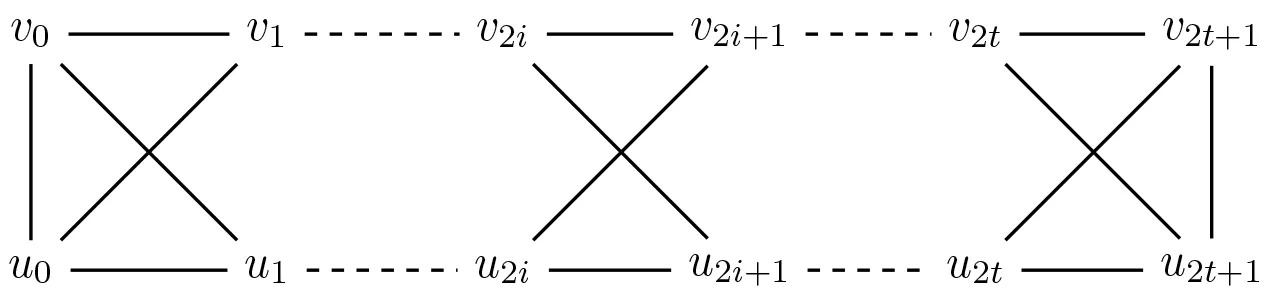
Figure 1. Graphs without cycles of length 1 modulo 4.

5 Graphs of chromatic number six

In this section, we consider graphs of chromatic number six and prove Theorem 1.2 for the casek=5. Very recently, Gao et al.[10]proved following theorems on cycles lengths in graphs containing a triangle.

Theorem 5.1LetGbe a connected graph of minimum degree at least three and (A,B) be a non-trivial partition ofV(G). For any cycleCinG, there existA-Bpaths of every length less than |V(C)| inG, unlessGis bipartite with the bipartition (A,B).

Theorem 5.2Letk≥3 be an integer andGbe a 2-connected graph of the minimum degree at leastk. IfGisK3-free, thenGcontains a cycle of length at least 2k+2, except thatG=Kk,nfor somen≥k.

Theorem 5.3Letk≥2 be an integer. Every 2-connected graphGof minimum degree at leastkcontaining a triangleK3containskcycles of consecutive lengths, except thatG=Kk+1.

Now, we are in a position to prove Theorem 1.2 for the casek=5, which we rephrase as follows.

Theorem 5.4Every 6-critical non-complete graphGcontains cycles of all lengths modulo 5.

ProofSuppose thatGdoes not contain cycles of all lengths modulo 5 andGis notK6. It is well-known thatGis a 2-connected graph of the minimum degree at least 5. By Theorem 5.3, we may assume thatGisK3-free. Fix a vertexrand letTbe a breadth-first search tree inGwith rootr. LetL0= {r} andLibe the set of vertices ofTat distanceifrom its rootr.

Claim 1Every component ofG[Li] has chromatic number at most 3, for alli≥0.

Proof of Claim 1Suppose to the contrary that there exists a componentDofG[Lt] which has chromatic number at least 4 for somet. LetHbe a 4-critical subgraph ofD. It is clear thatHis a 2-connected non-bipartite graph of minimum degree at least 3. By Theorem 5.2,Hcontains a cycle of length at least 8. LetT′ be the minimal subtree ofTwhose set of leaves is preciselyV(H), and letr′ be the root ofT′. Lethdenote the distance betweenr′ and vertices inHinT′. SinceGisK3-free,h≥2. By the minimality ofT′,r′ has at least two children inT′. Letxbe one of its children. LetAbe the set of vertices inHwhich are the descendants ofxinT′ and letB=V(H)-A. Then bothA,Bare nonempty and for anya∈Aandb∈B,Ta,bhas the same length 2h. By Theorem 5.1, there are 7 subpaths ofHfrom a vertex ofAto a vertex ofBof lengths 1, 2, …, 7, respectively. It follows thatGcontains 7 cycles of consecutive lengths, a contradiction. This completes the proof of Claim 1.

For a connected graphD, a vertex inDis called good if it is not contained in the minimal connected subgraph ofDwhich contains all 2-connected blocks ofD, and bad otherwise.

We now prove a claim which is key for the proof of Theorem 5.4.

Claim 2LetH1be a non-bipartite component ofG[Li] andH2be a non-bipartite component ofG[Li+1] for somei≥1. IfNH1(H2)≠Ø, then every vertex inNH1(H2) is a good vertex ofH1.

Proof of Claim 2Suppose that there exists a bad vertexvofH1which has a neighbor inH2. LetT′ be the minimal subtree ofTwhose set of leaves is preciselyV(H1), and letr′ be the root ofT′. Lethdenote the distance betweenr′ and vertices inH1inT′. SinceGisK3-free,h≥2. By the minimality ofT′,r′ has at least two children inT′. Let (X,Y) be a non-trivial partition of all children ofr′ inT′. LetAbe the set of vertices inH1which are the descendants ofXinT′ and letBbe the set of vertices inH1which are the descendants ofYinT′. Note that (A,B) is a non-trivial partition ofV(H1). Note that every vertex inBis the descendants ofYinT′. LetA′ be the set of vertices inLi-Awhich are the descendants ofXinT. LetB′ be the set of vertices inLi-Bwhich are the descendants ofYinT. LetM:=Li-(A∪A′∪B∪B′). Note thatA,A′,B,B′ andMform a partition ofLi. Note that every vertex ofH2has a neighbor inLi.

Suppose that there exists a vertexm∈V(H2) which has a neighborm′ inM. Recall thatH1is non-bipartite andK3-free. There exists a pathz1z2z3z4z5of length 4 inH1withz1=v. It is easy to see thatTzi, mcontainsr′ fori∈[5], so they have the same length. Sincevhas a neighbor inH2, there is a pathPfromvtominG[H2∪{v}]. ThenP∪z1z2…zi∪Tzi,m′∪m′m, fori∈[5] are 5 cycles of consecutive lengths inG, a contradiction. ThereforeNM(H2)=Ø, that is every vertex inH2has a neighbor inA∪A′∪B∪B′. For a vertex inV(H2), we call it type-Aif it has a neighbor inA∪A′ and it type-Bif it has a neighbor inB∪B′(2)We remark that a vertex can be both type-A and type-B..

LetC=v0v1…vnbe an odd cycle ofH1, wheren≥4. Suppose thatV(C)⊆A. SinceBis non-empty, we choose an arbitrary vertexbinB. SinceH1is connected, there exists a pathPfrombtoV(C) internal disjoint fromV(C). Without loss of generality, we assume thatV(P)∩V(C)={v0}. ThenP∪C[v0,vi]∪Tb,vifori=0, 1, …, 4 give 5 cycles of consecutive lengths, a contradiction. Therefore,B∩V(C)≠Ø, and similarly,A∩V(C)≠Ø. Then there must be anA-Bpath of length 4 inC(otherwise, since 4 and |C| are co-prime and |C|≥5, one can deduce that all vertices ofCare contained in one of the two partsAandB, a contradiction).

Without loss of generality, we may assume thatv0,v1∈Aandv2∈B. ThenTv1,v2∪v2v1andTv0,v2∪v2v1v0are two cycles of lengths 2h+1 and 2h+2, respectively. We have showed that there exists someA-Bpath of length 4 inCwhich gives a cycle of length 2h+4, so we may assume that there is noA-Bpath of length 3 or 5 inC. This would force that one of the following holds.

5.1 There is no A-B path of length 3 in H1

This would force that for any pathP′=u0u1…usinH1withu1=v0,u2=v1,u3=v2, we can derive thatuj∈Bifj≡0 mod 3 anduj∈Aifj≡1 or 2 mod 3. Moreover, we have thatv3i,v3i+1∈Aandv3i+2∈Bfor each possiblei≥0. So |C|≥9 andGcontains a cycle of lengthl∈{2h+1, 2h+2, 2h+4, 2h+5, 2h+7, 2h+8}. In particular, sinceH1is connected, for any vertexb∈B, there exists a path of length 2 inH1frombto some vertex inA. And for any bad vertexa∈A, there exists a pathb1aa1b2satisfyingb1,b2∈Banda,a1∈A.

Suppose thatNA∪A′(H2)≠Ø andNB∪B′(H2)≠Ø. SinceH2is connected and every vertex ofH2has a neighbor inA∪A′∪B∪B′, there exist two adjacent verticesp,qofH2such thatphas a neighborp′ inA∪A′ andqhas a neighborq′ inB∪B′. Thenp′pqq′∪Tp′,q′is a cycle of length 2h+3. It follows thatGcontains 5 cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+5, respectively, a contradiction.

Suppose thatNLi(H2)⊆B∪B′. SinceNA∪B(H2)≠Ø, we have thatv∈B. Letube any vertex inNH2(v). Choosew1∈V(H2) such that there exists a pathQof length 2 fromutow1inH2. Since any vertex inH2has a neighbor inLi, by our assumption,w1has a neighbor inB∪B′. Letw2be a neighbor ofw1inB∪B′. Suppose thatw2≠v. Note that there is a pathR:=vv″v′ such thatv′,v″∈A. ThenR∪vu∪Q∪w1w2∪Tw2, v′is a cycle of length 2h+6. SoGcontains cycles of lengths 2h+4, 2h+5, 2h+6, 2h+7 and 2h+8, a contradiction. Thereforew2=vandw1∈NH2(v). That says, every vertex inH2of distance 2 from a neighbor ofvis a neighbor ofv. Continuing to apply this along with a path fromuto an odd cycleC0inH2, we could obtain thatvis adjacent to all vertices ofC0, which contradicts thatGisK3-free. Therefore,NB∪B′(H2)=Ø.

Now we see thatNLi(H2)⊆A∪A′. This forces thatv∈A. For any neighboru′ ofvinH2, letw3∈V(H2) satisfies that there exists a pathQ′ of length 2 fromu′ tow3inH2. Note thatv∈Ais bad inH1, we can infer that there exists a pathb2va1b1inH1such thata1∈Aandb1,b2∈B. Note thatvanda1are symmetric. Letw4be a neighbor ofw3inA∪A′. Suppose thatw4∉{v,a1}. Thenvu′∪Q′∪w3w4∪Tw4, b1∪b1a1vis a cycle of length 2h+6. So again,Gcontains cycles of lengths 2h+4, 2h+5, 2h+6, 2h+7 and 2h+8, a contradiction. Therefore,w4∈{v,a1}. That is, every vertex inH2of distance 2 from a neighbor ofvora1is adjacent to one ofv,a1. Continuing to apply this along with a path fromu′ to an odd cycleC1inH2, we could obtain that every vertex ofC1is adjacent to one ofv,a1. But this would force a copy ofK3containinga1vinG. This final contradiction completes the proof of this subsection.

5.2 There is an A-B path of length 3 in H1

Therefore, we may assume that there is noA-Bpaths of length 5 inH1.

We first show that for any patht1t2t3inH1satisfying thatt1andt3are in different parts,t2does not have a neighbor inV(H2); call this Property ★. Suppose to the contrary thatt2has a neighbor inH2. Without loss of generality, we may assume thatt1,t2∈Aandt3∈B. Letsbe any vertex inNH2(t2). Chooses′∈V(H2) such that there exists a pathQof length 2 fromstos′ inH2. Lettbe a neighbor ofs′ inLi-M. Suppose thatt≠t2. Ift∈A∪A′, thent3t2s∪Q∪s′t∪Tt, t3is a cycle of length 2h+5. SoGcontains cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+5, a contradiction. Thereforet∈B∪B′, thent1t2s∪Q∪s′t∪Tt, t1is a cycle of length 2h+5. SoGcontains cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+5, a contradiction. Thereforet=t2ands′ is the neighbor oft2. That says, every vertex inH2of distance 2 from a neighbor oft2is a neighbor oft2. Continuing to apply this along with a path fromsto an odd cycleC2inH2, we could obtain thatt2is adjacent to all vertices ofC2, which contradicts thatGisK3-free.

Suppose thatNA∪A′(H2)≠Ø andNB∪B′(H2)≠Ø. Suppose that there exists a pathp0p1p2p3inH2such thatp0is type-Aandp3is type-B. Letqbe the neighbor ofp0inA∪A′ andq′ be the neighbor ofp3inB∪B′. Thenqp0p1p2p3q′∪Tq′, qis a cycle of length 2h+5. SoGcontains cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+5, a contradiction. This forces that every two vertices which are linked by a path of length 3 inH2have the same type. Note thatNA∪A′(H2)≠Ø andNB∪B′(H2)≠Ø. By symmetry betweenA∪A′ andB∪B′, there exists a pathz0z1z2inH2such thatz0andz1are type-Aandz2is type-B. Moreover, for any pathP″:=u0u1…usinH2withu0=z0,u1=z1,u2=z2, we can derive thatujis type-Aifj≡0 or 1 mod 3 andujis type-Bifj≡2 mod 3. Moreover, for any pathP‴:=u0u1…usinH2withu0=z2,u1=z1,u2=z0, we can derive thatujis type-Bifj≡0 mod 3 andujis type-Aifj≡1 or 2 mod 3. This forces that every cycle inH2has length 0 modulo 3. SinceH2is non-bipartite andK3-free, there is an odd cycleC3:=w0w1…wmw0of length at least 9. Note thatw0andw8have different types. If follows that there is a cycle of length 2h+10. SoGcontains cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+10, a contradiction.

Therefore, all vertices inH2have the same type. Without loss of generality, we may assume thatNLi(H2)⊆A∪A′. Thereforev∈Aand letf0be a neighbor ofvinH2. SinceH2isK3-free and non-bipartite, there is a pathf0f1f2inH2. SinceH1is aK3-free non-bipartite graph andvis a bad vertex inH1, there is a patha0a1va2a3inH1. Since there is noA-Bpath of length 5 inH1, we have that for any pathQ′:=u0u1…usinH1withu0=a0,u1=a1,u2=v,u3=a2,u4=a3, we can derive thatujandukare in the same part ifj≡kmod 5. Also, we have that for any pathQ′:=u0u1…usinH1withu0=a3,u1=a2,u2=v,u3=a1,u4=a0, we can derive thatujandukare in the same part ifj≡kmod 5. By Property ★, we have thata1anda2are in the same part ofH1.

Suppose thata1,a2∈A. SinceV(H1)∩B≠Ø, we have that one ofa0anda3is inB. Without loss of generality, we may assume thata0∈B. Letwbe a neighbor off1inH1. We have thatw∈A∪A′. SinceGisK3-free,w≠v. Note thata0a1vsatisfying thata0andvare in different parts ofH1. By Property ★, we have thatw≠a1. Therefore,wf1f0va1a0∪Ta0, wis a cycle of length 2h+5. SoGcontains cycles of lengths 2h+1, 2h+2, 2h+3, 2h+4 and 2h+5, a contradiction.

This completes the proof of Claim 2.

Now, we define a coloringc:V(G)→{1, 2, 3, 4, 5} as follows. LetDbe any bipartite component ofG[Li] for somei. Ifiis even, we color one part ofDwith color 1 and the other part with color 2, and ifiis odd, we color one part ofDwith color 4 and the other part with color 5. LetFbe any non-bipartite component ofG[Lj] for somej. Ifjis even, by using the block structure ofF, we can properly colorV(F) with colors 1, 2 and 3 by coloring bad vertices with colors 1, 2 and 3 and coloring good vertices with colors 1 and 2. Ifjis odd, then we also can properly colorV(F) with colors 3, 4 and 5 by coloring bad vertices with colors 3, 4 and 5 and coloring good vertices with colors 4 and 5.

Next, we argue thatcis a proper coloring onG. LetH1be a component ofG[Li] andH2be a component ofG[Li+1] fori≥0 such that there exists an edge betweenH1andH2. If one of them is bipartite, thencis proper onV(H1)∪V(H2). Therefore, bothH1andH2are non-bipartite. By the above claim, all vertices ofH2are not adjacent to vertices of color 3 inH1. It follows thatcis proper onV(H1)∪V(H2). Therefore,cis a proper 5-coloring ofG, which contradicts thatGis 6-critical. This completes the proof of Theorem 5.4.

Proof of Theorem 1.2LetGbe a (k+1)-critical non-complete graph, fork∈{4, 5}. Suppose thatk=4. It is well-known thatGis a 2-connected graph of minimum degree at least 4. Then by Theorem 4.1,Gcontains cycles of all lengths modulo 4. Suppose thatk=5. By Theorem 5.4,Gcontains cycles of all lengths modulo 5.