The stable subgroups of Sn acting on M0,n

Xia Xiaopeng

School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026,China

Abstract: Considering the action of the symmetric group Sn on M0,n, all the possible stable subgroups were obtained.

Keywords: moduli space; symmetric group; group action; stable subgroup

1 Introduction

The moduli space of the Riemann sphere withn-marked points is

M0,n={(x1,…,xn)∈

The symmetric groupSnnaturally acts on M0,n. For anyσ∈Snand any [x1,…,xn]∈M0,n, we have

σ·[x1,…,xn]=[xσ(1),…,xσ(n)].

Ref.[1] investigated the locus with nontrivial stable subgroups, and proved that the stable subgroups must be cyclic. However, we find examples with the stable subgroups being cyclic groups, dihedral groups,A4,S4, orA5. In this paper, we study stable subgroups on M0,n,n≥4, and obtain all types of stable subgroups. For the convenience of description, we introduce the following notations. We writeζd,d≥1, to denote the primitived-th root of unity in, and writeto denote the image ofA∈GL2() in the projective general linear group PGL2(). Letx∈M0,n, then the stable subgroup ofxis

Stab(x)={σ∈Sn|σ·x=x}.

We first prove that the stable subgroup is isomorphic to a finite subgroupGof PGL2(), and then obtain the types ofp-subgroups by using the properties of elements inG, and then obtain the types of finite subgroups in PGL2(). Then we obtain the classification of stable subgroups (see Theorem 2.1). Finally, we further discuss stable subgroups for a more accurate description (see Proposition 3.1), and show the existence of these possible types by some examples (see Example 3.1).

2 Finite subgroups of PGL2()

Theorem 2.1Letx∈M0,n, then Stab(x) is isomorphic to a cyclic group, a dihedral group,A4,S4orA5.

Proposition 2.1Letx∈M0,n, then Stab(x) is isomorphic to a finite subgroup of PGL2().

Therefore, we need to consider the types of finite subgroups of PGL2().

Lemma 2.1LetGbe a finite subgroup of PGL2(), and letLetA1have characteristic subspacesVλ1,Vλ2belonging to eigenvaluesλ1,λ2. Then:

(ii) The proof of (ii) is trivial by (i).

(iii) We getA2Vλi=Vλifori=1,2 by (i). Then there exists a matrixP∈M2(), such that

Lemma 2.2[2]

(ⅰ) The dihedral group of order 2nhas a presentationD2n=〈a,b|an=b2=(ab)2=1〉.

(ⅱ) The alternating groupA4has a presentationA4=〈a,b|a3=b3=(ab)2=1〉.

(ⅲ) The symmetric groupS4has a presentationS4=〈a,b|a4=b2=(ab)3=1〉.

(ⅳ) The alternating groupA5has a presentationA5=〈a,b|a5=b2=(ab)3=1〉.

Lemma 2.3LetGbe a finite subgroup of PGL2(), and letPbe ap-subgroup ofG. Then:

(ⅰ) Ifp>2, thenPis cyclic.

(ⅱ) Ifp=2, thenPis a cyclic group or dihedral group.

Proof(i) Let |P|>1, so |Z(P)|>1, thenPis abelian by Lemma 2.1(ii). Letg∈Psuch thato(g)=max{o(g′)|∀g′∈P}, then for anyg′∈P, we getg,g′∈〈gg′〉=〈g〉 by Lemma 2.1(iii). HencePis cyclic.

and let

P=〈b,g|go(g)=b2=(bg)2=1〉

is a dihedral group.

Lemma 2.4[2]Let all Sylow subgroups of a finite groupGbe cyclic groups. IfGis commutative, thenGis a cyclic group; ifGis not commutative, thenGis a metacyclic group determined by the following definition relationship:

G=〈a,b〉,am=bn=1,b-1ab=ar,

gcd((r-1)n,m)=1,rn≡1(modm),|G|=nm.

Lemma 2.5[3]LetGbe a finite group, and letO(G) be the largest normal subgroup of odd order inG. IfGhas dihedral Sylow 2-subgroups, thenG/O(G) is isomorphic to either

(ⅰ) a subgroup of Aut(PSL(2,pn)) containing PSL(2,pn), where Aut(PSL(2,pn)) is isomorphic to the semidirect product of PGL(2,pn) by a cyclic group of ordernandpis an odd prime,

(ⅱ) the alternating groupA7, or

(ⅲ) a Sylow 2-subgroup ofG.

Theorem 2.2LetGbe a finite group. ThenGis isomorphic to a subgroup of PGL2() if and only ifGis isomorphic to a cyclic group, a dihedral group,A4,S4orA5.

ProofSuppose thatGis isomorphic to a subgroup of PGL2(). LetMbe the largest normal subgroup of odd order inG. If |M|>1, we supposeMis not cyclic. By Lemma 2.3 and Lemma 2.4, we have

M=〈a,b〉,ad=bk=1,b-1ab=ar,

gcd((r-1)k,d)=1,rk≡1(modd),|M|=kd.

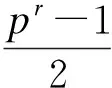
Conversely, letGbe isomorphic to a cyclic group, a dihedral group,A4,S4orA5. According to Lemma 2.2, we use the same method mentioned above and solve the equations, then we obtain that there is a subgroupG′ in PGL2() such thatG′ is isomorphic toG.

3 Types of stable subgroups

Forx∈M0,n, we further discuss Stab(x) in this section for a more accurate description.

Lemma 3.1Letx∈M0,n, and letσ∈Stab(x)(1)}. Then:

(ⅰ)A complete factorization ofσhasr11-cycles andr2d-cycles, where 0≤r1≤2 andr1+r2d=n.

(ⅱ) If there isτ∈Stab(x) such thatσ≠τandτστ-1=σ-1. Then |{i|σ(i)=i}|≠1.

Proposition 3.1Letx∈M0,n. Then one of the following holds:

(ⅰ) Stab(x) is a cyclic group of orderm, wherem|norm|n-1 orm|n-2.

(ⅱ) Stab(x) is a dihedral group of order 2m, wherem|norm|n-2.

(ⅲ) Stab(x) is isomorphic toA4orS4.

(ⅳ) Stab(x) is isomorphic toA5.

ProofThe proof is trivial by Theorem 2.1 and Lemma 3.1.

From Proposition 3.1, we can get the possible types of stable subgroups. Next, we do not fixn, and then prove the existence of these possible types by some examples.

Lemma 3.2Letx∈M0,n. Then:

(ⅰ) If Stab(x) is isomorphic toA4, thenn≡0,4,6,8(mod 12).

(ⅱ) If Stab(x) is isomorphic toS4, thenn≡0,6,8,12(mod 24).

(ⅲ) If Stab(x) is isomorphic toA5, thenn≡0,12,20,30(mod 60).

ProofConsider Stab(x) acts on the set {1,2,…,n}. For any 1≤i≤n, the stabilizer ofi, denoted byGi, does not contain dihedral groups by Lemma 3.1, then the size of the orbit ofiis |Stab(x)|/|Gi|, whereGiis cyclic. Therefore, the conclusion is obtained by Lemma 3.1.

Example 3.1The following examples show that each finite subgroup of PGL2() happens as a stable subgroup.

it follows that (1 5)(2 4)(3 6)∈Stab(x). According to Proposition 3.1, it follows that Stab(x) is isomorphic toS4.

it follows that

(1 12)(2 5)(3 10)(4 6)(7 9)(8 11)∈Stab(x).

According to Proposition 3.1, it follows that Stab(x) is isomorphic toA5.

it follows that

τ=(2n)(3n-1)…(dn+2-d)∈Stab(x),

(ⅴ) Letx=[1,-1,0,∞]∈M0,4. Then Stab(x)={(1),(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)}≅D4.

it follows that

σ=(1 2 …n)(n+1n+2 … 2n)∈Stab(x).

Then Stab(x) is isomorphic to a cyclic group orA4by Lemma 3.1(ii) and Proposition 3.1. According to Lemma 3.2, it follows that Stab(x) is not isomorphic toA4, then Stab(x) is cyclic. Since

it follows that Stab(x) is a cyclic group of ordern.

(ⅷ) Letx=[x1,x2,…,xn]∈M0,n,n≥5, wherexi∈for 1≤i≤nandxnis transcendental over(x1,…,xn-1). Suppose there is (1)≠σ∈Stab(x). Then there is)such that

Soa,b,c∈(x1,…,xn-1). Butthenxnis algebraic over(x1,…,xn-1). This leads to a contradiction. Hence Stab(x)={(1)}.